Уравнение Шредингера — основное уравнение нерелятивистской квантовой механики, описывающее динамику частиц. Предложено Э.Шредингером в 1926 г. Состояние классической частицы в любой момент времени описывается заданием ее координат и импульсов (x,y,z,px,py,pz). Зная эти величины в момент времени t, можно определить эволюцию системы под действием известных сил во все последующие моменты времени. Координаты и импульсы частиц сами являются величинами, непосредственно измеряемыми на опыте. В квантовой физике состояние системы описывается волновой функцией ψ(x,y,z,t). Т. к. для квантовой частицы нельзя одновременно точно определить значения ее координат и импульса, то не имеет смысла говорить о движении частицы по определенной траектории, можно определить только вероятность нахождения частицы в данной точке в данный момент времени, которая определяется квадратом модуля волновой функции W ~ |ψ(x,y,z,t)|2. Эволюция квантовой системы в нерелятивистском случае описывается волновой функцией, удовлетворяющей уравнению Шредингера 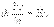 где ψ(x,y,z,t) − волновая функция,
где ψ(x,y,z,t) − волновая функция, 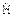 − оператор Гамильтона (оператор полной энергии системы).
− оператор Гамильтона (оператор полной энергии системы).
В нерелятивистском случае 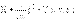 где m − масса частицы,
где m − масса частицы, 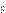 − оператор импульса,
− оператор импульса, 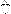 (x,y,z,t) − оператор потенциальной энергии частицы. Задать закон движения частицы в квантовой механике это значит определить значение волновой функции в каждый момент времени в каждой точке пространства. Уравнение Шредингера играет в квантовой механике такую же роль, как и второй закон Ньютона в классической механике.
(x,y,z,t) − оператор потенциальной энергии частицы. Задать закон движения частицы в квантовой механике это значит определить значение волновой функции в каждый момент времени в каждой точке пространства. Уравнение Шредингера играет в квантовой механике такую же роль, как и второй закон Ньютона в классической механике.
В стационарном состоянии Ψ (x, y, z, t) = ψ(x, y, z)e-iEt/ћ.
Так как вероятность найти частицу в момент t в точке x, y, z пропорциональна
|Ψ(x, y, z, t )|2 , то в данном случае она ~ |ψ (x, y, z)|2, т.е. не зависит от времени. Аналогично, вероятность обнаружить значение физической величины, характеризующей систему, также не изменяется со временем, т.к. выражается через квадраты модулей волновых функций.
Уравнение Шредингера для стационарного состояния, когда потенциальная энергия частицы явным образом не зависит от времени, имеет вид 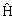 ψ(x, y, z) = Eψ(x, y, z). Это уравнение называют стационарным уравнением Шредингера.
ψ(x, y, z) = Eψ(x, y, z). Это уравнение называют стационарным уравнением Шредингера.
Одна из специфических особенностей квантовых систем состоит в том, что энергетические спектры частиц, находящихся в ограниченном объеме пространства дискретны.
2) ВОЛНОВАЯ ФУНКЦИЯ (или вектор состояния) – комплексная функция, описывающая состояние квантово-механической системы. Её знание позволяет получить максимально полные сведения о системе, принципиально достижимые в микромире. Так с её помощью можно рассчитать все измеряемые физические характеристики системы, вероятность пребывания её в определенном месте пространства и эволюцию во времени. Волновая функция может быть найдена в результате решения волнового уравнения Шредингера.
Волновая функция ψ(x, y, z, t) ≡ ψ(x,t) точечной бесструктурной частицы является комплексной функцией координат этой частицы и времени. Простейшим примером такой функции является волновая функция свободной частицы с импульсом 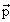 и полной энергией Е (плоская волна)
и полной энергией Е (плоская волна)
Волновая функция системы А частиц содержит координаты всех частиц: ψ( 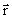 1,
1, 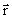 2,...,
2,..., 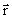 A,t).
A,t).
Квадрат модуля волновой функции отдельной частицы |ψ( 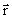 ,t)|2 = ψ*(
,t)|2 = ψ*( 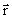 ,t)ψ(
,t)ψ( 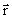 ,t) дает вероятность обнаружить частицу в момент времени t в точке пространства, описываемой координатами
,t) дает вероятность обнаружить частицу в момент времени t в точке пространства, описываемой координатами 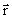 , а именно, |ψ(
, а именно, |ψ( 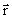 ,t)|2dv ≡ |ψ(x, y, z, t)|2dxdydz это вероятность найти частицу в области пространства объемом dv = dxdydz вокруг точки x, y, z. Аналогично, вероятность найти в момент времени t систему А частиц с координатами
,t)|2dv ≡ |ψ(x, y, z, t)|2dxdydz это вероятность найти частицу в области пространства объемом dv = dxdydz вокруг точки x, y, z. Аналогично, вероятность найти в момент времени t систему А частиц с координатами 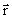 1,
1, 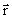 2,...,
2,..., 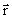 A в элементе объема многомерного пространства дается величиной |ψ(
A в элементе объема многомерного пространства дается величиной |ψ( 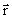 1,
1, 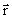 2,...,
2,..., 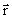 A,t)|2dv1dv2...dvA.
A,t)|2dv1dv2...dvA.
Волновая функция полностью определяет все физические характеристики квантовой системы. Так среднее наблюдаемое значение физической величины F у системы дается выражением 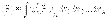 где
где 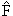 - оператор этой величины и интегрирование проводится по всей области многомерного пространства.
- оператор этой величины и интегрирование проводится по всей области многомерного пространства.
В качестве независимых переменных волновой функции вместо координат частиц x, y, z могут быть выбраны их импульсы px, py, pz или другие наборы физических величин. Этот выбор зависит от представления (координатного, импульсного или другого).
Волновая функция ψ( 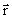 ,t) частицы не учитывает ее внутренних характеристик и степеней свободы, т. е. описывает ее движение как целого бесструктурного (точечного) объекта по некой траектории (орбите) в пространстве. Этими внутренними характеристиками частицы могут быть её спин, спиральность, изоспин (для сильновзаимодействующих частиц), цвет (для кварков и глюонов) и некоторые другие. Внутренние характеристики частицы задаются специальной волновой функцией её внутреннего состояния φ. При этом полная волновая функция частицы Ψ может быть представлена в виде произведения функции орбитального движения ψ и внутренней функции φ: Ψ = φψ, поскольку обычно внутренние характеристики частицы и её степени свободы, описывающие орбитальное движение, не зависят друг от друга. В качестве примера ограничимся случаем, когда единственной внутренней характеристикой, учитываемой функцией
,t) частицы не учитывает ее внутренних характеристик и степеней свободы, т. е. описывает ее движение как целого бесструктурного (точечного) объекта по некой траектории (орбите) в пространстве. Этими внутренними характеристиками частицы могут быть её спин, спиральность, изоспин (для сильновзаимодействующих частиц), цвет (для кварков и глюонов) и некоторые другие. Внутренние характеристики частицы задаются специальной волновой функцией её внутреннего состояния φ. При этом полная волновая функция частицы Ψ может быть представлена в виде произведения функции орбитального движения ψ и внутренней функции φ: Ψ = φψ, поскольку обычно внутренние характеристики частицы и её степени свободы, описывающие орбитальное движение, не зависят друг от друга. В качестве примера ограничимся случаем, когда единственной внутренней характеристикой, учитываемой функцией 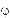 , является спин частицы, причем этот спин равен 1/2. Частица с таким спином может пребывать в одном из двух состояний − с проекцией спина на ось z, равной +1/2 (спин вверх), и с проекцией спина на ось z, равной -1/2 (спин вниз). Эту двойственность описывают спиновой функцией
, является спин частицы, причем этот спин равен 1/2. Частица с таким спином может пребывать в одном из двух состояний − с проекцией спина на ось z, равной +1/2 (спин вверх), и с проекцией спина на ось z, равной -1/2 (спин вниз). Эту двойственность описывают спиновой функцией 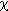 взятой в виде двухкомпонентного спинора:
взятой в виде двухкомпонентного спинора: 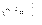
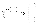 Тогда волновая функция Ψ+1/2 = χ+1/2ψ будет описывать движение частицы со спином 1/2, направленным вверх, по траектории, определяемой функцией ψ , а волновая функция Ψ-1/2 = χ-1/2ψ будет описывать движение по той же траектории этой же частицы, но со спином, направленным вниз.
Тогда волновая функция Ψ+1/2 = χ+1/2ψ будет описывать движение частицы со спином 1/2, направленным вверх, по траектории, определяемой функцией ψ , а волновая функция Ψ-1/2 = χ-1/2ψ будет описывать движение по той же траектории этой же частицы, но со спином, направленным вниз.
В заключении отметим, что в квантовой механике возможны такие состояния, которые нельзя описать с помощью волновой функции. Такие состояния называют смешанными и их описывают в рамках более сложного подхода, использующего понятие матрицы плотности. Состояния квантовой системы, описываемые волновой функцией, называют чистыми.
Дата: 2019-07-24, просмотров: 325.