Процесс возбуждения электромагнитных волн какой-либо системой в окружающем пространстве называется излучением этих волн, а сама система называется излучающей системой. Поле электромагнитных волн называется полем излучения. Простейшим излучателем электромагнитных волн является электрический диполь, электрический момент которого изменяется по гармоническому закону 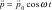  Примером подобного диполя может служить система, состоящая из покоящегося положительного заряда + q и отрицательного заряда − q , гармонически колеблющегося вдоль направления rp с частотой ω. Как показывает теория, в точках пространства, отстоящих от диполя на расстояниях r , значительно превышающих длину излучаемой волны r >> λ (эта область пространства называется волновой зоной диполя), интенсивность излучения диполя: 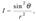где θ — угол между осью диполя и направлением излучения. Зависимость I(θ ) при фиксированном r называют полярной диаграммой направленности излучения диполя (индикатрисой излучения). Из этой диаграммы видно, что диполь сильнее всего излучает в направлениях, перпендикулярных его оси θ=(π/2). Вдоль своей оси (θ = 0 и θ = π ) диполь не излучает вообще. Диаграмма направленности позволяет формировать излучение с определенными пространственными характеристиками и используется при конструировании антенн.

Шкала электромагнитных волн. Электромагнитные волны, обладая широким диапазоном частот (или длин волн), отличаются по способам их генерации и регистрации, а также по своим свойствам. Поэтому электромагнитные волны условно делятся на несколько видов: радиоволны (λ >50мкм), световые волны (инфракрасные волны (770нм<λ <1мм) видимый свет (380нм<λ <770нм), ультрафиолетовое излучение (10нм<λ <380нм)), рентгеновское излучение (0,01нм<λ <100нм) и γ -излучение (λ <0,1нм).

ОПТИКА

ГЕОМЕТР . ОПТИКА

Оптика — раздел физики, который изучает природу света, световые явления и взаимодействие света с веществом. Оптическое излучение представляет собой электромагнитные волны, и поэтому оптика является частью общего учения об электромагнитном поле. В зависимости от круга рассматриваемых явлений оптику делят на геометрическую лучевую), волновую физическую), квантовую (корпускулярную). Основные законы геометрической оптики. Еще до установления природы света были известны следующие законы: Закон прямолинейного распространения света — свет в оптически однородной среде распространяется прямолинейно. Световой луч — линия, вдоль которой переносится световая энергия. В однородной среде лучи света представляют собой прямые линии. Закон независимости световых пучков — эффект, производимый отдельным пучком, не зависит от того, действуют ли одновременно остальные пучки или они устранены. Закон отражения — отраженный луч лежит в одной плоскости с падающим лучом и перпендикуляром, проведенным к границе раздела двух сред в точке падения; угол отражения i1′ равен углу падения I1: .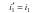

Закон преломления — луч падающий, луч преломленный и перпендикуляр, проведенный к границе раздела двух сред в точке падения, лежат в одной плоскости; отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных сред 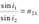, где n21— относительный показатель преломления второй среды относительно первой, который равен отношению абсолютных показателей преломления двух сред 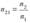. Следовательно, закон преломления будет иметь вид:  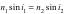Абсолютным показателем преломления среды называется величина n , равная 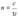отношению скорости электромагнитных волн в вакууме c к их фазовой скорости υ в среде. Поскольку υ = c εµ , то n = εµ , где ε и µ — соответственно электрическая и магнитная проницаемость среды.

Энергетические величины в фотометрии. Фотометрия — раздел оптики, в котором рассматриваются энергетические характеристики оптического излучения в  процессах его испускания, распространения и взаимодействия с веществом. При этом значительное внимание уделяется вопросам измерения интенсивности света и его источников. Энергетические величины в фотометрии — характеризуют энергетические параметры оптического излучения без учета особенностей его воздействия на тот или иной приемник излучения. Поток излучения Φ e — величина, равная отношению энергии W излучения ко времени t , за которое излучение произошло (мощность излучения). Единица потока излучения — ватт (Вт) .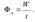

Энергетическая светимость (излучательность) R e -величина, равная отношению потока излучения Φ e, испускаемого поверхностью, к площади S сечения, сквозь которое этот поток проходит (поверхностная плотность потока излучения). Единица энергетической светимости — ватт на метр в квадрате (Вт/м2) 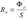.                                                                                           Энергетическая сила света (сила излучения) Ie — величина, равная отношению потока излучения Φe точечного источника к телесному углу ω , в пределах которого это излучение распространяется. Единица энергетической силы света — ватт на стерадиан (Вт/ср).

Энергетическая яркость (лучистость) Be — величина, равная отношению энергетической силы света ∆Ie элемента излучающей поверхности к площади ∆S проекции этого элемента на плоскость, перпендикулярную направлению наблюдения. Единица энергетической яркости — ватт на стерадиан-метр в квадрате (Вт/(ср·м2)). 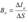Энергетическая освещенность (облученность) Ee — характеризует величину потока излучения, падающего на единицу освещаемой поверхности. Единица энергетической освещенности — ватт на метр в квадрате (Вт/м2).

Световые величины в фотометрии. Различные приемники, используемые при оптических измерениях, обладают селективностью (избирательностью). Для каждого из них характерна своя кривая чувствительности к энергии различных длин волн. Световые измерения, являясь субъективными, отличаются от объективных, энергетических, и для них вводятся световые единицы, используемые только для видимого света. Основной световой единицей в СИ является единица силы света I — кандела (кд) — сила света в заданном направлении источника, испускающего монохроматическое излучение частотой 540·1012 герц, энергетическая сила света которого в этом направлении составляет 1683 Вт/ср. Единица светового потока Φ (мощности оптического излучения) — люмен (лм): 1лм — световой поток, испускаемый точечным источником силой света в 1кд внутри телесного угла в 1ср (1лм=1кд·ср). Светимость R — суммарный поток, посылаемый светящейся площадкой с площадью S . Единица светимости — люмен на метр в квадрате (лм/м2) Яркость светящейся поверхности в некотором направлении ϕ есть величина, равная отношению силы света I в этом направлении к площади S проекции светящейся поверхности на плоскость, перпендикулярную данному направлению. Единица яркости — кандела на метр в квадрате (кд/м2).   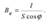Освещенность E  — величина, равная отношению светового потока Φ , падающего на поверхность, к площади S этой поверхности. Единица освещенности — люкс (лк): 1лк — освещенность поверхности, на один квадратный метр которой падает световой поток в 1лм (1лк=1лм/м2).

2. ЛИНЗОЙ называется прозрачное тело, ограниченное с двух сторон криволинейной поверхностью

 (В частном случае одна из поверхностей может быть плоской). По внешней форме линзы делятся на 1) двояковыпуклые; 2) плосковыпуклые; 3) двояковогнутые; 4) плосковогнутые; 5) выпукло-вогнутые. Линза называется тонкой, если ее толщина значительно меньше, чем радиусы кривизны R1 и R2 обеих поверхностей. На оптических схемах линзы обычно обозначают двунаправленной стрелкой. Радиус кривизны R > 0 для выпуклой поверхности; R < 0 для вогнутой.

Прямая проходящая через центры кривизны поверхностей линзы называется главной оптической осью. Оптическим центром линзы (обычно обозначается O ) называется точка, лежащая на главной оптической оси и обладающая тем свойством, что лучи проходят сквозь нее не преломляясь.

Побочными оптическими осями называются прямые, проходящие через оптический центр линзы и не совпадающие с главной оптической осью. Фокусом линзы F называется точка, лежащая на главной оптической оси, в которой пересекаются лучи параксиального (приосевого) светового пучка, распространяющиеся параллельно главной оптической оси. Фокальной плоскостью называется плоскость, проходящая через фокус линзы перпендикулярно ее главной оптической оси.

Фокусным расстоянием f называется расстояние между оптическим центром линзы O и ее фокусом F :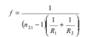

Формула тонкой линзы: 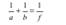где a и b — расстояния от линзы до предмета и его изображения. Если a = ∞ , т.е. лучи падают на линзу параллельным пучком (а), то b = f . Если b = ∞ , т.е. изображении находится в бесконечности (б), и, следовательно, лучи выходят из линзы параллельным пучком, то a = f . Фокусные расстояния линзы, окруженной с обеих сторон одинаковой средой, равны. Величина Φ =1 f называется оптической силой линзы. Ее единица —диоптрия (дптр) — оптическая сила линзы с фокусным расстоянием 1м

Линзы с положительной оптической силой являются собирающими, с отрицательной —рассеивающими. В отличие от собирающей линзы, рассеивающая линза имеет мнимые фокусы. В мнимом фокусе сходятся после преломления) воображаемые продолжения лучей, падающих на рассеивающую линзу параллельно главной оптической оси.

Аберрации оптических систем. В реальных оптических системах используются пучки отличающиеся от параксиальных, показатель преломления линз зависит от длины волны падающего света, а сам свет немонохроматичен. Искажения оптического изображения которые возникают при этом называются аберрациями.

Сферическая аберрация. Фокус S′′ для лучей, более удаленных от оптической оси чем параксиальные, находится ближе, чем фокус S′ параксиальных лучей. В результате  изображение светящейся точки имеет вид расплывчатого пятна. Сферическая аберрация является частным случаем астигматизма.

Кома. Если через оптическую систему проходит широкий пучок от точечного источника света, расположенного не на оптической оси, то получаемое изображение этой точки будет в виде освещенного пятна неправильной формы.

Точечным источником света называется источник, размерами которого можно пренебречь.

Астигматизм. Погрешность, обусловленная неодинаковостью кривизны оптической поверхности в разных плоскостях сечения падающего на нее светового пучка

Дисторсия. Погрешность, при которой при больших углах падения лучей на линзу линейное увеличение для точек предмета, которые находятся на разных расстояниях от главной оптической оси, несколько различается. В результате нарушается геометрическое подобие между предметом (например, прямоугольная сетка) и его изображением р(исунок (b) —подушкообразная дисторсия, (c) — бочкообразная дисторсия).

Хроматическая аберрация.При падении на оптическую систему белого света отдельные составляющие его монохроматические лучи фокусируются в разных точках н(аибольшее фокусное расстояние имеют красные лучи, наименьшее — фиолетовые), поэтому изображение размыто и по краям окрашено.

3. ИНТЕРФЕРЕНЦИЯ СВЕТА. Интерференция света — сложение в пространстве двух или нескольких когерентных световых волн, при котором в разных его точках получается усиление или ослабление амплитуды результирующей волны. Пусть в данной точке M две монохроматические волны с циклической частотой ω возбуждают два колебания, причем до точки M одна волны прошла в среде с показателем преломления n1 путь s1 с фазовой скоростью υ1 , а вторая — в среде n2 путь s2 с фазовой скоростью υ2 :  Амплитуда результирующего колебания: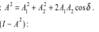

Интенсивность результирующей волны :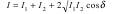

Разность фаз δ колебаний, возбуждаемых в точке M , равна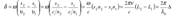

(Использовали: υ = c n ; ω = 2πν ; c ν = λ0 — длина волны в вакууме). Произведение геометрической длины пути s световой волны в данной среде на показатель преломления этой среды n называется оптической длиной пути L = s ⋅ n. Разность ∆ = L2 − L1 = s2n2 − s1n1 оптических длин проходимых волнами путей называется оптической разностью хода. Условие интерференционного максимума: Если оптическая разность хода ∆ равна целому числу длин волн в вакууме (четному числу полуволн)

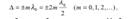то δ = ±2mπ и колебания, возбуждаемые в точке M , будут происходить в одинаковой фазе. Условие интерференционного минимума. Если оптическая разность хода ∆ равна нечетному числу полуволн

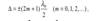то δ = ±(2m +1)π и колебания, возбуждаемые в точке M , будут

происходить в противофазе.

Методы наблюдения интерференции. До изобретения лазеров, во всех приборах когерентные световые пучки получали разделением волны, излучаемой одним источником, на две части, которые после прохождения разных оптических путей накладывали друг на друга и наблюдали интерференционную картину.

1. Метод Юнга. Свет от ярко освещенной щели S падает на две щели S1 и S2, играющие роль когерентных источников. Интерференционная картина BC наблюдается на экране Э.

2. Зеркала Френеля.  Свет от источника S падает расходящимся пучком на два плоских зеркала A1O и A2O , расположенных под малым углом ϕ . Роль когерентных источников играют мнимые S1 и S2 изображения источника S . Интерференционная картина наблюдается на экране Э, защищенном от прямого попадания света заслонкой З.      

3.Бипризма Френеля. Свет от источника S преломляется в призмах, в результате чего за бипризмой распространяются световые лучи, как бы исходящие из мнимых когерентных источников S1 и S2.

4. Зеркало Ллойда. Точечный источник S находится близко к поверхности плоского зеркала M . Когерентными источниками служат сам источник S и его мнимое изображение S1.

Кольца Ньютона. Кольца Ньютона, являющиеся классическим примером полос равной толщины, наблюдаются при отражении света от воздушного зазора, образованного плоскопараллельной пластинкой и соприкасающейся с ней плосковыпуклой линзой с большим радиусом кривизны. Параллельный пучок света падает нормально на плоскую поверхность  линзы. Полосы равной толщины имеют вид концентрических окружностей. С учетом d2 → 0

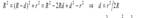 В отраженном свете оптическая разность хода: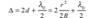

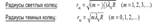
Интерференцию можно наблюдать и в проходящем свете, причем в проходящем свете максимумы интерференции соответствуют минимумам интерференции в отраженном свете и наоборот.

4. ПРОСВЕТЛЕНИЕ ОПТИКИ. Объективы оптических приборов содержат большое  количество линз. Даже незначительное отражение света каждой из поверхностей линз приводит к тому, что интенсивность прошедшего пучка света значительно уменьшается. Кроме того, в объективах возникают блики и фон рассеянного света, что снижает эффективность оптических систем. Но, если на границах сред создать условия, при которых интерференция отраженных лучей 1’ и 2" дает минимум интенсивности отраженного света, то при этом интенсивность света, прошедшего через оптическую систему будет максимальна. Этого можно добиться, например, нанесением на поверхность линз тонких пленок с показателем преломления 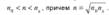. В этом случае амплитуды когерентных лучей 1’ и 2" будут одинаковы, а условие минимума для отраженных лучей (i = 0) будет 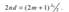. При m = 0 оптическая толщина пленки nd удовлетворяет условию 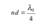и происходит гашение отраженных лучей. Для каждой длины волны λ0 должна быть своя толщина пленки d . Поскольку этого добиться невозможно, обычно оптику просветляют для длины волны λ0 = 550 нм, к которой наиболее чувствителен глаз человека.

Информетры. При плавном изменении разности хода интерферирующих пучков на λ/2интерференционная картина сместится настолько, что на месте максимумов окажутся минимумы. Поэтому явление интерференции используют в интерферометрах для измерения длины тел, длины световой волны, изменения длины тела при изменении температуры, сравнимых с λ0

В интерферометре Майкельсона монохроматический луч от источника S разделяется на полупрозрачной пластинке P1 на два луча 1’ и 2", которые, отразившись от зеркал M1 и M2 , снова с помощью P1 сводятся в один пучок, в котором лучи 1' и 2" формируют интерференционную картину. Компенсационная пластинка P2 размещается на пути луча 2, чтобы он так же, как и луч 1, дважды прошел через пластинку. Возникающая интерференционная картина чрезвычайно чувствительна к любому изменению разности хода лучей, (например, к смещению одного из зеркал).

5. ПРИНЦИП ГЮЙГЕНСА-ФРЕНЕЛЯ. Дифракцией называется огибание волнами препятствий, встречающихся на их пути, или в более широком смысле — любое отклонение распространения волн вблизи препятствий от законов геометрической оптики. Дифракцию объясняет принцип Гюйгенса — именно вторичные волны огибают препятствия на пути распространения первичных волн. Френель дополнил принцип Гюйгенса представлением о когерентности вторичных волн и их интерференции. Согласно принципу Гюйгенса-Френеля, световая волна, возбуждаемая каким-либо источником S , может быть представлена как результат суперпозиции (сложения) когерентных вторичных волн, излучаемых вторичными (фиктивными) источниками — бесконечно малыми элементами любой замкнутой поверхности, охватывающей источник S .

18. Зоны Френеля. Рассмотрим в произвольной точке M амплитуду световой волны, распространяющейся в однородной среде из точечного источника S . Согласно принципу Гюйгенса-Френеля, заменим действие источника S действием воображаемых источников, расположенных на вспомогательной поверхности Φ , являющейся поверхностью фронта волны, идущей из S (поверхность сферы с центром S). Разобьем волновую поверхность Φ на кольцевые зоны такого размера, чтобы расстояния от краев зоны до M отличались на λ/2.

Тогда, обозначив амплитуды колебаний от 1-й, 2-й, … m-й зон через A1, A2, …Aм (при этом A1 > A2 > A3 >K), получим амплитуду результирующего колебания: A = A1 − A2 + A3 − A4 + K. При таком разбиении волновой поверхности на зоны оказывается, что амплитуда колебания Am от некоторой m-й зоны Френеля равна среднему арифметическому от амплитуд примыкающих к ней зон

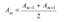
Радиус внешней границы m-й зоны Френеля 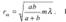                                            При ab= = 10см и λ = 500нм радиус первой зоны r1 = 0,158мм. Следовательно, распространение света от S к M происходит так, будто световой поток распространяется внутри очень узкого канала вдоль SM , т.е. прямолинейно. Таким образом, принцип Гюйгенса-Френеля позволяет объяснить прямолинейное распространение света в однородной среде.

6. ДИФРАКЦИЯ НА ПРОСТРАНСТВЕННОЙ РЕШЕТКЕ. Дифракция света наблюдается на одномерных решетках (система параллельных штрихов), на двумерных решетках (штрихи нанесены во взаимно перпендикулярных направлениях в одной и той же плоскости) и на пространственных (трехмерных) решетках — пространственных образованиях, в которых элементы структуры подобны по форме, имеют геометрически правильное и периодически повторяющееся расположение, а также постоянные (периоды) решеток, соизмеримые с длиной волны электромагнитного излучения. Кристаллы, являясь трехмерными пространственными образованиями с постоянной решетки порядка 10–10м, могут быть использованы для наблюдения дифракции рентгеновского излучения (λ ≈10−12 ч10−8м) . Представим кристалл в виде параллельных кристаллографических плоскостей, отстоящих друг от друга на расстоянии d . Пучок параллельных монохроматических лучей (1, 2) падает под углом скольжения ϑ (угол между направлением падающих лучей и кристаллографической плоскостью) и возбуждает атомы кристаллической решетки, которые становятся источниками когерентных вторичных волн (1’ и 2’), интерферирующих между собой. Максимумы интенсивности  будут наблюдаться в тех направлениях, в которых все отраженные атомными плоскостями волны будут находиться в одинаковой фазе: 2d sinϑ = mλ (m =1,2,3,K) — формула Вульфа–Брэггов. Эта формула используется в: 1) рентгеноструктурном анализе — если известна λ рентгеновского излучения, то, наблюдая дифракцию на кристаллической структуре неизвестного строения и измеряя ϑ и m , можно найти d , т.е. определить структуру вещества; 2) рентгеновской спектроскопии — если известна d , то измеряя ϑ и m, можно найти длину волны λ падающего рентгеновского

7. ДИСПЕРСИЯ СВЕТА. Дисперсией света называется зависимость показателя преломления n от частоты ν (длины волны λ ) света (или зависимость фазовой скорости υ световых волн от его частоты ν ). Следствием дисперсии является разложение в спектр пучка белого света при прохождении его через призму. Дисперсия проявляется лишь при распространении немонохроматических волн.

Для всех прозрачных веществ показатель преломления уменьшается с увеличением длины волны: dn/dλ<0 (см. рисунок). Такая дисперсия называется нормальной (или отрицательной). Вблизи линий и полос сильного поглощения ход кривой n(λ) — кривой дисперсии — обратный:dn/dλ>0. Такая дисперсия называется аномальной.

 На явлении нормальной дисперсии основано действие призменных спектрографов. Угол отклонения лучей призмой зависит от показателя преломления, который в свою очередь, зависит от длины волны. Поэтому призма разлагает белый свет в спектр, отклоняя красные лучи (длина волны больше) слабее, чем фиолетовые (длина волны меньше).

Электронная теория дисперсии. Электронная теория дисперсии Лоренца рассматривает дисперсию света как результат взаимодействия электромагнитных волн с заряженными частицами, входящими в состав вещества и совершающими вынужденные колебания в переменном электромагнитном поле волны. Абсолютный показатель преломления среды n = 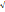εµ , где ε — диэлектрическая проницаемость среды, µ — магнитная проницаемость. В оптической области спектра для всех веществ µ ≈1, поэтому n =  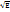Согласно теории Лоренца, дисперсия света — следствие зависимости ε от частоты (длины волны) световых волн. По определению 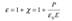, где χ — диэлектрическая восприимчивость среды, ε0 — электрическая постоянная, P и E — мгновенные значение поляризованности и напряженности внешнего электрического поля. В оптической области спектра частота колебаний электрического поля световой волны высока (ν ≈1013Гц), поэтому ориентационная поляризация диэлектриков несущественна, и главную роль играет электронная (деформационная) поляризация — вынужденные колебания электронов под действием электрической составляющей поля световой волны. Пусть вынужденные колебания совершает только один внешний, слабо связанный с ядром атома, электрон — оптический электрон. Его наведенный дипольный момент: p = ex , где e — заряд электрона, x — смещение электрона под действием электрического поля световой волны. Мгновенное значение поляризованности: P = n0 p = n0ex , где n0- концентрация атомов в диэлектрике. Отсюда: ∆λ/2 зон. Все точки волнового фронта в плоскости щели имеют одинаковую фазу и амплитуду колебаний. Поэтому суммарная интенсивность колебаний от двух любых соседних зон Френеля равна нулю. Следовательно: 1) если число зон Френеля четное, то: 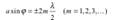— условие дифракционного минимума (полная темнота).

2) если число зон Френеля нечетное, то 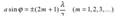— условие дифракционного максимума,соответствующего действию одной некомпенсированной зоны Френеля. В направлении ϕ = 0 щель действует как одна зона Френеля и в этом направлении свет распространяется с наибольшей интенсивностью — центральный дифракционный максимум. Направления, в которых амплитуда максимальна или равна нулю:

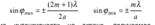Распределение интенсивности на экране, получаемое вследствие дифракции, называется дифракционным спектром (рисунок (б)). Интенсивности в центральном и последующих максимумах относятся как 1: 740,0:710,0:3800,0:…, т.е.  основная часть световой энергии сосредоточена в центральном максимуме. Положение дифракционных максимумов зависит от λ . При освещении щели белым светом, центральный максимум наблюдается в виде белой полоски (при ϕ = 0 разность хода  равна нулю для всех λ ) — он общий для всех длин волн. Боковые максимумы радужно окрашены фиолетовым краем к центру дифракционной картины (поскольку λфиол < λкрасн ).

8. ЕСТЕСТВЕННЫЙ И ПОЛЯРИЗОВАННЫЙ СВЕТ. При действии света на вещество основное значение имеет электрическая составляющая электромагнитного поля световой волны, поскольку именно она оказывает основное действие на электроны в атомах вещества. Поэтому, для описания закономерностей поляризации будем рассматривать только световой вектор — вектор напряженности E электрического поля.

Свет представляет собой суммарное электромагнитное излучение множества независимо излучающих атомов. Поэтому все ориентации вектора E будут равновероятны. Такой свет называется естественным (рис. (а)).

Поляризованным светом называется свет, в которомнаправления колебания вектора E каким-либо образом упорядочены. Частично поляризованный свет (рис. (б)) — свет с

 преимущественным направлением колебаний вектора E.

Плоскополяризованный свет — свет в котором вектор E колеблется только в одной, проходящей через луч плоскости (рис. (в) на предыдущей странице и рис. (а) и (б) на этой).

Эта плоскость называется плоскостью поляризации. Если концы вектора E с течением времени описывают в плоскости, перпендикулярной лучу,окружность или эллипс (рис.(в)), то свет называется циркулярно или эллиптически поляризованным. Степенью поляризации называется величина P : 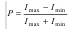, где 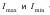— соответственно, максимальная и минимальная интенсивности частично поляризованного света. Для естественного света 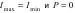, для плоскополяризованного I min = 0 и P =1. Естественный свет можно преобразовать в плоскополяризованный, используя так называемые поляризаторы, пропускающие колебания только определенного направления. В качестве поляризаторов используются среды, анизотропные в отношении вектора колебаний E.

Закон Малюса.

Пропустим естественный свет с интенсивностью Iест через поляризатор T1. Колебание амплитуды A, совершающееся в  плоскости, образующей с плоскостью поляризатора угол ϕ , можно разложить на два колебания с амплитудами A = Acosϕ и A⊥ = Asinϕ . Интенсивность прошедшей волны пропорциональна 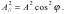. В естественном свете все значения ϕ равновероятны, поэтому доля света, прошедшего через поляризатор, будет равна среднему значению (cos2ϕ) = 1/2, а интенсивность плоскополяризованного света, прошедшего через первый поляризатор T1: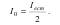

Поставим на пути плоскополяризованного света второй поляризатор T2 (анализатор) под углом ψ к первому. Интенсивность I света, прошедшего через анализатор, меняется в зависимости от угла ψ по закону Малюса Следовательно, интенсивность света, прошедшего через два поляризатора: 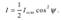.  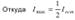когда поляризаторы параллельны и Imin = 0 , когда поляризаторы скрещены.