Представление об атомах как неделимых мельчайших частицах вещества возникло еще в античные времена. В 1903 г. Джозеф Джон Томсон предложил первую модель атома: атом представляет собой непрерывно заряженный положительным электрическим зарядом шар, внутри которого около своих положений равновесия колеблются электроны; суммарный заряд электронов равен положительному заряду шара, поэтому атом в целом нейтрален. Однако предположение о непрерывном распределении положительного заряда внутри атома не подтвердилось экспериментом.
Экспериментальная проверка модели атома Томсона была осуществлена в 1911г. английским физиком Эрнестом Резерфордом. Он провел опыты по рассеянию альфа-частиц в веществе. Альфа-частицы испускаются при радиоактивных превращениях. Их электрический заряд положителен и равен по модулю двойному заряду электрона. Это тяжелые частицы: масса их примерно в 7 300 раз больше массы электрона. Исследуя прохождение альфа-частиц через золотую фольгу, Резерфорд обнаружил, что основная их часть испытывает незначительные отклонения, а некоторые из них (примерно, одна из 20 000) резко отклоняются от первоначального направления — вплоть до 180°. Поскольку электроны не могут существенно повлиять на характер движения столь тяжелых и быстрых альфа-частиц, Резерфорд сделал вывод: значительное отклонение альфа-частиц обусловлено их взаимодействием с положительным зарядом большей массы. Такое отклонение испытывали лишь немногие альфа-частицы, т. е. те, которые оказались вблизи положительного заряда сравнительно небольших размеров.
Анализируя результаты опытов, Резерфорд предложил ядерную (планетарную) модель атома: вокруг положительного ядра, имеющего заряд Ze ( Z— порядковый номер элемента в системе Менделеева, е - элементарный заряд), по замкнутым орбитам движутся электроны, образуя электронную оболочку атома. Движущиеся по замкнутым орбитам электроны обладают центростремительным ускорением. Согласно классической электродинамике, ускоренные электроны излучают электромагнитные волны, вследствие чего непрерывно теряют энергию. Поэтому электрон, вращаясь вокруг ядра, излучает энергию. В результате потери энергии, двигаясь по спирали и приближаясь к ядру, он в конце концов упадет на него. Таким образом, атом в модели Резерфорда оказался неустойчивой системой.
Попытки создать модель атома в рамках классической физики не привели к успеху: модель Томсона была опровергнута опытами Резерфорда, планетарная же модель не смогла объяснить устойчивость атомов. Преодоление возникших трудностей потребовало создания - квантовой -теории атома. Однако, несмотря на свою несостоятельность, планетарная модель и сейчас принята в качестве приближенной и упрощенной картины атома.
2. Планетарная модель атома, предложенная Резерфордом, – это попытка применения классических представлений о движении тел к явлениям атомных масштабов. Она оказалась несостоятельной. Классический атом неустойчив.
Первый постулат Бора (постулат стационарных состояний) гласит: атомная система может находится только в особых стационарных или квантовых состояниях, каждому из которых соответствует определенная энергия En. В стационарных состояниях атом не излучает.
Второй постулат Бора (правило частот) формулируется следующим образом: при переходе атома из одного стационарного состояния с энергией En в другое стационарное состояние с энергией Em излучается или поглощается квант, энергия которого равна разности энергий стационарных состояний:
Существование дискретных энергетических уровней атома подтверждается опытом Франка и Герца. Немецкие ученые Джеймс Франк и Густав Герц за экспериментальные исследования дискретности энергетических уровней получили Нобелевскую премию в 1925 г.
В опытах использовалась трубка (рис. 6.9), заполненная парами ртути при давлении р ≈ 1 мм рт. ст. и три электрода: катод, сетка и анод.
Электроны ускорялись разностью потенциалов U между катодом и сеткой. Эту разность потенциалов можно было изменять с помощью потенциометра П. Между сеткой и анодом тормозящее поле 0,5 В (метод задерживающих потенциалов).
Опыт показал, что электроны передают свою энергию атомам ртути порциями, причем 4,86 эВ – наименьшая возможная порция, которая может быть поглощена атомом ртути в основном энергетическом состоянии. Следовательно, идея Бора о существовании в атомах стационарных состояний блестяще выдержала проверку экспериментом.
Атомы ртути, получившие при соударении с электронами энергию , переходят в возбужденное состояние и должны вернуться в основное, излучая при этом, согласно второму постулату Бора, квант света с частотой . По известному значению можно вычислить длину волны светового кванта: . Таким образом, если теория верна, то атомы ртути, бомбардируемые электронами с энергией 4,86 эВ, должны являться источником ультрафиолетового излучения с , что действительно обнаружилось в опытах.
2.ВОЛНЫ ДЕ БРОЙЛЯ.В ЧЕМ ЗАКЛЮЧАЕТСЯ ОПЫТ ДЭВИССОНА-ДЖЭРМЕРА
Волны де Бройля – волны, связанные с любой движущейся материальной частицей. Любая движущаяся частица (например, электрон) ведёт себя не только как локализованный в пространстве перемещающийся объект - корпускула, но и как волна, причём длина этой волны даётся формулой λ = h/р, где h = 6.6·10-34 Дж.сек – постоянная Планка, а р – импульс частицы. Эта волна и получила название волны де Бройля. Если частица имеет массу m и скорость v << с (с – скорость света), то импульс частицы р = mv и дебройлевская длина волны связаны соотношением λ = h/mv.
Волновые свойства макроскопических объектов не проявляются из-за малых длин волн. Однако для микрочастиц длины волн лежат в доступной наблюдению области.
Для расчёта длины волны де Бройля частицы массы m, имеющей кинетическую энергию E, удобно использовать соотношение 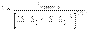 где E0 = mc2 − энергия покоя частицы массы m, λкомптон = h/mc − комптоновская длина волны частицы, λкомптон (электрон) = 2.4·10-12 м = 0.024 Å, λкомптон (протон) = 1.32·10-15 м = 1.32 фм. Длина волны де Бройля фотона с энергией Е определяется из соотношения λ(фм) = h/p = hc/E = 2π·197 МэВ·фм /E(МэВ).
где E0 = mc2 − энергия покоя частицы массы m, λкомптон = h/mc − комптоновская длина волны частицы, λкомптон (электрон) = 2.4·10-12 м = 0.024 Å, λкомптон (протон) = 1.32·10-15 м = 1.32 фм. Длина волны де Бройля фотона с энергией Е определяется из соотношения λ(фм) = h/p = hc/E = 2π·197 МэВ·фм /E(МэВ).
Существование волн де Бройля доказано многочисленными экспериментами, в которых частицы ведут себя как волны. Так при рассеянии пучка электронов с энергией 100 эВ на упорядоченной системе атомов кристалла, играющего роль дифракционной решётки, наблюдается отчётливая дифракционная картина. Метод дифракции частиц в настоящее время широко используется при изучении строения и свойств вещества.
2)Опыт Дэвиссона-Джермера — физический эксперимент по дифракцииэлектронов, проведённый в 1927 г. американскими учёными Клинтоном Дэвиссоном и Лестером Джермером.
Идея опыта
Проводилось исследование отражения электронов от монокристалланикеля. Установка включала в себя монокристалл никеля, сошлифованный под углом, и установленный на держателе. На плоскость шлифанаправлялся перпендикулярно пучок монохроматических электронов.Скорость электронов определялась напряжением  на электронной пушке:
на электронной пушке: 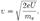
Под углом  к падающему пучку электронов устанавливался цилиндрФарадея, соединённый с чувствительным гальванометром. По показаниямгальванометра определялась интенсивность отражённого от кристаллаэлектронного пучка. Вся установка находилась в вакууме.
к падающему пучку электронов устанавливался цилиндрФарадея, соединённый с чувствительным гальванометром. По показаниямгальванометра определялась интенсивность отражённого от кристаллаэлектронного пучка. Вся установка находилась в вакууме.
В опытах измерялась интенсивность рассеянного кристаллом электронногопучка в зависимости от угла рассеяния 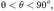 от азимутального угла
от азимутального угла 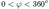 , от скорости
, от скорости  электронов в пучке.
электронов в пучке.
Опыты показали, что имеется ярко выраженная селективность(выборочность) рассеяния электронов. При различных значениях углов искоростей, в отражённых лучах наблюдаются максимумы и минимумыинтенсивности. Условие максимума: 
Здесь d — постоянная кристаллической решётки.
Таким образом наблюдалась дифракция электронов на кристаллическойрешётке монокристала. Опыт явился блестящим подтверждениемсуществования у микрочастиц волновых свойств.
Соотношение называется соотношением неопределенностей для величин A и B. Это соотношение ввёл в 1927 году Вернер Гейзенберг.
Утверждение о том, что произведение неопределенностей значений двух сопряженных переменных не может быть по порядку меньше постоянной Планка h, называется соотношением неопределенностей Гейзенберга.
Соотношение неопределенностей получено при одновременном использовании классических характеристик движения частицы (координаты, импульса) и наличии у нее волновых свойств. Т.к. в классической механике принимается, что измерение координаты и импульса может быть произведено с любой точностью, то соотношение неопределенностей является, таким образом, квантовым ограничением применимости классической механики к микрообъектам.
Дата: 2019-07-24, просмотров: 330.