Если у нас имеется термодинамическая система состоящая из N частиц, энергии которых могут принимать дискретные значения Е₁, Е₂…Е_n, то говорят о системе квантовых чисел.
Поведение такой системы описывается квантовой статистикой, в основе которой лежит принцип неразличимости тождественных частиц. Основная задача этой статистики состоит в определении среднего числа 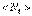частиц, находящихся в ячейке фазового пространства: «координаты – проекции импульса» (x, y, z и p_x, p_y, p_z) частиц. При этом имеют место два закона распределения частиц по энергиям (две статистики):

распределение Бозе – Эйнштейна: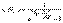

распределение Ферми – Дирака: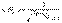

Здесь µ – химический потенциал.
Первая формула описывает квантовые частицы с целым спином (собственный момент количества движения). Их называют бозоны (например, фотоны). Вторая формула описывает квантовые частицы с полуцелым спином. Их называют фермионы (например: электроны, протоны, нейтрино).

Распределение электронов в атоме происходит по принципу Паули, который может быть сформулирован для атома в простейшем виде: в одном и том же атоме не может быть более одного электрона с одинаковым набором четырех квантовых чисел: n, l, , :Z (n, l, , ) = 0 или 1, где Z (n, l, , ) - число электронов, находящихся в квантовом состоянии, описываемых набором четырех квантовых чисел: n, l, , . Таким образом, принцип Паули утверждает, что два электрона, связанные в одном и том же атоме различаются значениями, по крайней мере, одного квантового числа.                                        Максимальное число электронов, находящихся в состояниях, описываемых набором трех квантовых чисел n, l и m, и отличающихся только ориентацией спинов электронов равно: ибо спиновое квантовое число может принимать лишь два значения 1/2 и –1/2.                                                   Максимальное число электронов, находящихся в состояниях, определяемых двумя квантовыми числами n и l: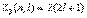

8 РЕНТГЕНОВСКИЕ СПЕКТРЫ          Рентгеновские спектры - спектры испускания и поглощения рентгеновского излучения. Рентгеновские спектры могут быть непрерывными или линейчатыми. Линейчатый Р. с. испускают атомы и ионы после ионизации их внутр. оболочек при последующем заполнении образовавшихся вакансий; такой Рентгеновский спектр наз. характеристическим, т. к. однозначно характеризует излучаемый атом. Непрерывным является тормозной Рентгеновские спектры, спектр синхротронного излучения в рентг. диапазоне. Характеристические рентгеновские спектры состоят из спектральных серий (К, L, M, N, О), все линии каждой из к-рых объединены общим начальным уровнем ионизации; уровни энергии, с к-рых происходит квантовый переход при заполнении образовавшейся вакансии для линий одной серии различны. Вероятность излучат. переходов разл. мультипольности, а следовательно, и интенсивность соответствующих спектральных линий определяются различными отбора правилами .Переходы для наиб. ярких линий К- и L-серий, а также обозначения этих линий приведены на рис. 1. Линии одной серии элементов образуют одинаковые группы дублетов, что позволило дать им одинаковые для всех ат. номеров Z обозначения греческими или латинскими буквами. Зависимость спектрального положения одноимённых линий от Z определяется Мозли законом.                 2) Мозли закон - утверждает, что корень квадратный из частоты v характеристич. рентг. излучения атома хим. элемента и его ат. номер Z связаны линейной зависимостью: 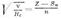      (R_с- Ридберга постоянная, S_n - постоянная экранирования, учитывающая влияние на отд. электрон всех остальных электронов атома, n - гл. квантовое число). Мозли закон установлен экспериментально в 1913 Г. Мозли (H. Moseley). Графически зависимость 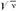от Z представляет собой ряд прямых (К-, L-, M- и т. д. серии, соответствующие n=1,2,3,...; рис.). Мозли закон окончательно подтвердил, что Z определяется не массой атомного ядра, а его зарядом. Мозли закон - основа рентг.спектрального анализа.                                 

3) В конце 19 века Планк исследовал проблему излучения абсолютно чёрного тела, которую за 40 лет до этого сформулировал Кирхгоф. Нагретые тела светятся тем сильнее, чем выше их температура и больше внутренняя тепловая энергия. Теплота распределяется между всеми атомами тела, приводя их в движение друг относительно друга и к возбуждению электронов в атомах. При переходе электронов к устойчивым состояниям излучаются фотоны, которые могут снова поглощаться атомами. При каждой температуре возможно состояние равновесия между излучением и веществом, при этом доля энергии излучения в общей энергии системы зависит от температуры. В состоянии равновесия с излучением абсолютно чёрное тело не только поглощает всё падающее на него излучение, но и излучает само то же самое количество энергии, по определённому закону распределения энергии по частотам..

Планк предположил, что поведение света подобно движению набора множества одинаковых гармонических осцилляторов. Он изучал изменение энтропии этих осцилляторов в зависимости от температуры, пытаясь обосновать закон Вина, и нашёл подходящую математическую функцию для спектра чёрного тела Однако вскоре Планк понял, что кроме его решения возможны и другие, приводящие к другим значениям энтропии осцилляторов. Одним из новых принятых Планком условий было: интерпретировать U_N (энергия колебаний N осцилляторов) не как непрерывную неограниченно делимую величину, а как дискретную величину, состоящую из суммы ограниченных равных частей. Обозначим каждую такую часть в виде элемента энергии через ε;^[2] С этим новым условием Планк фактически вводил квантованность энергии осцилляторов, говоря, что это "чисто формальное предположение … на самом деле я не думал об этом глубоко…",^[4]однако это привело к настоящей революции в физике. Применение нового подхода к закону смещения Вина показало, что "элемент энергии" должен быть пропорционален частоте осциллятора. Это было первой версией того, что сейчас называется "формула Планка": 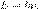Планку удалось вычислить значение h из экспериментальных данных по излучению чёрного тела: его результат был 6,55 • 10⁻³⁴ Дж•с, с точностью 1,2 % от принятого сейчас значения.^[2] Он также смог впервые определить постоянную Больцмана k_B из тех же данных и своей теории.^[5]

До теории Планка предполагалось, что энергия тела может быть любой, являясь непрерывной функцией. Это эквивалентно тому, что элемент энергии ε (разность между дозволенными уровнями энергии) равен нулю, следовательно должна быть равна нулю и h. Исходя из этого следует понимать утверждения о том, что "постоянная Планка равна нулю в классической физике" или что "классическая физика является пределом квантовой механики при устремлении постоянной Планка к нулю". Вследствие малости постоянной Планка она почти не проявляется в обычном человеческом опыте и до работ Планка была незаметна.

Проблема чёрного тела была пересмотрена в 1905 г., когда Рэлей и Джинс с одной стороны, и Эйнштейн с другой стороны, независимо доказали, что классическая электродинамика не может обосновать наблюдаемый спектр излучения. Это привело к так называемой "ультрафиолетовой катастрофе", обозначенной таким образом Эренфестом в 1911 г. Усилия теоретиков (вместе с работой Эйнштейна по фотоэффекту) привели к признанию того, что постулат Планка о квантовании уровней энергии является не простым математическим формализмом, а важным элементом представлений о физической реальности.

 9.ФОТОЭФФЕКТ. Фотоэлементы и их применение.

Фотоэффект - испускание электронов с поверхности металла под действием света.

Законы фотоэффекта были установлены А.Г.Столетовым.

1. Сила фототока прямо пропорциональна плотности светового потока.

2. максимальная кинетическая энергия вырываемых светом электронов линейно возрастает с частотой света и не зависит от его интенсивности.

3. для каждого вещества при определенном состоянии его поверхности существует граничная частота света, ниже которой фотоэффект не наблюдается. Эта частота и соответствующая длина волны называется красной границей фотоэффекта.

Теоретически это доказал Эйнштейн. Согласно ему, электромагнитное излучение представляет собой поток отдельных квантов (фотонов) с энергией hν каждый, где h — постоянная Планка. При фотоэффекте часть падающего электромагнитного излучения от поверхности металла отражается, а часть проникает внутрь поверхностного слоя металла и там поглощается. 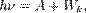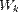Поглотив фотон, электрон получает от него энергию и, совершая работу выхода A, покидает металл: где — максимальная кинетическая энергия, которую имеет электрон при вылете из металла.

Внешним фотоэффектом (фотоэлектронной эмиссией) называется испускание электронов веществом под действием электромагнитных излучений. Электроны, вылетающие из вещества при внешнем фотоэффекте, называются фотоэлектронами, а электрический ток, образуемый ими при упорядоченном движении во внешнем электрическом поле, называется фототоком.

Фотоэлемент — электронный прибор, который преобразует энергию фотонов в электрическую энергию. Подразделяются на электровакуумные и полупроводниковые фотоэлементы^[1]. Действие прибора основано на фотоэлектронной эмиссии или внутреннем фотоэффекте^.