Для чего применяется движение по градиенту? Рассмотрим схему, где изображены кривые равного выхода поверхности отклика для двух независимых переменных (линии/поверхности уровня). Собственно поверхность отклика имеет вид “холма” с вершиной. Если пытаться попасть к вершине (т.е. найти оптимум!) методом однофакторного эксперимента, то сначала необходимо, фиксировав один фактор, менять другой до тех пор, пока увеличивается выход. Затем аналогично осуществляем движение по второму фактору. При большом количестве факторов решение будет достаточно сложным и продолжительным. Наиболее короткий путь – определение градиента функции отклика. При реализации метода крутого восхождения движение к оптимальной области осуществляется в направлении градиента функции отклика, а именно, в направлении вектора
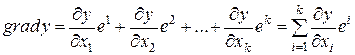 ,
,
где 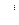 - единичные векторы осей для независимых переменных.
- единичные векторы осей для независимых переменных.
Метод крутого восхождения осуществляется поэтапно. Сначала проводят полный факторный или дробный эксперимент в окрестности исходной точки. После статистической обработки экспериментальных данных вычисляются коэффициенты регрессии линейной модели. Далее с учётом величины и знака коэффициентов регрессии рассчитывают несколько, так называемых мысленных опытов. Движение осуществляется изменением факторов пропорционально величине коэффициентов уравнения регрессии в ту сторону, в которую указывает знак коэффициента. Движение к оптимуму осуществляется по наиболее крутому пути, что и дало название методу.
Движение по градиенту для одномерного поиска показано на фиг.3.3. Коэффициент регрессии численно равен тангенсу угла между линией регрессии и осью данного фактора ( 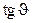 соответствует частной производной функции отклика по данному фактору). Катет АС в треугольнике АВС есть не что иное как интервал варьирования
соответствует частной производной функции отклика по данному фактору). Катет АС в треугольнике АВС есть не что иное как интервал варьирования  фактора. Отрезок АВ указывает направление движения к оптимальной области. Величина шага изменяется путём деления или умножения его на положительное число Это соответствует перемещению точки
фактора. Отрезок АВ указывает направление движения к оптимальной области. Величина шага изменяется путём деления или умножения его на положительное число Это соответствует перемещению точки 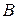 по градиенту без изменения направления движения к оптимальной области.
по градиенту без изменения направления движения к оптимальной области.
Характер движения к оптимальной области при двумерном поиске показан на фиг.3.4.

При определёнии значений факторов для мысленных опытов к основному уровню в направлении градиента прибавляются величины с некоторым шагом, величина которого определяет скорость поиска. При малом шаге поиск ведётся медленно; чрезмерное увеличения его приводит к "проскакиванию" оптимальной области. На практике величину шага выбирают так, чтобы в области факторного пространства можно было сделать 5-10 шагов. При этом шаг в 2-3 раза должен превышать ошибки измерения данного фактора. Во всяком случае, аналогично выбору интервалов варьирования, нижняя граница задается исходя из возможности фиксирования двух факторов, а верхняя связана с областью определения факторов. Величина шага варьирования каждого фактора при крутом восхождении пропорциональна значению коэффициента регрессии; чем больше этот коэффициент, тем большее влияние оказывает фактор. В связи с этим шаг изменения фактора берут пропорционально произведению коэффициента
регрессии на интервал варьирования. Новые значения факторов подставляют в уравнение регрессии и вычисляют ожидаемые значения функции отклика. Далее реализуют опыты с наибольшим значением функции отклика. При этом используются раскодированные значения факторов.
Качественные факторы при движении к оптимуму фиксируют на лучшем уровне. Незначимые факторы стабилизируют на любом уровне - чаще на нулевом, иногда на нижнем. В движении по градиенту эти факторы не участвуют.
Иногда имеет смысл оценить ожидаемы значения параметра оптимизации в мысленных опытах. Число мысленных опытов зависит о задачи. Ограничением сверху служит область определения хотя бы по одному из факторов (в нашем случае это фактор  ). Как реализовать мысленные опыты? Если модель адекватна, то реализацию начинают с опытов, условия которых выходят за область определения хотя бы по одному из факторов. Для неадекватной модели один-два опыта проводят в области эксперимента.
). Как реализовать мысленные опыты? Если модель адекватна, то реализацию начинают с опытов, условия которых выходят за область определения хотя бы по одному из факторов. Для неадекватной модели один-два опыта проводят в области эксперимента.
Иногда после каждого опыта проводится анализ результатов и принимается решение относительно хода эксперимента. В другом варианте ставятся одновременно два-три опыта и принимается решение. Иногда при выборе порядка реализации мысленных опытов применяют метод "ножниц": выполняют два крайних опыта, а затем "прощупывается" пространство внутри интервала.
Пример (поиск оптимума в трёхмерном пространстве). Допустим, что в результате реализации матрицы полного факторного эксперимента  получено уравнение регрессии:
получено уравнение регрессии:
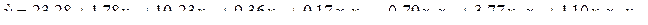 По формуле
По формуле 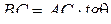 рассчитаем величины шага факторов:
рассчитаем величины шага факторов:
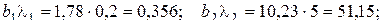
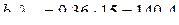 .
.
Расчётную величину шага необходимо прибавить к основному уровню. Однако после этого в опыте №10 (табл. 3.13) факторы будут иметь не реальные значения. Следовательно, шаг движения велик. Для уменьшения шага разделим его величину на некоторое положительное число. В результате получим точки лежащие на градиенте.
Таблица 3.13
Оптимальный поиск методом крутого восхождения
| № опыта | Факторы | у,% | |||
| Уровни варьирования | С, г/л | 
| 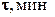
| Выход | |
| Верхний уровень (+) | 0,9 | 140 | 45 | продукта | |
| Основной уровень (0) | 0,7 | 135 | 30 | ||
| Нижний уровень (-1) | 0,5 | 130 | 15 | ||
| Интервал варьирования | 0,2 | 5 | 15 | ||

| 
| 
| |||
| 1 | + | + | + | 46,8 | |
| 2 | + | + | - | 24,15 | |
| 3 | - | + | + | 46,5 | |
| 4 | - | + | - | 16,63 | |
| 5 | + | - | + | 20,47 | |
| 6 | + | - | - | 8,89 | |
| 7 | - | - | + | 16,80 | |
| 8 | - | - | - | 5,08 | |
Коэффициент регрессии 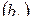
| +1,78 | +10,23 | +9,36 | ||
Произведение 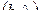
| +0,356 | +51,40 | +140 | ||
| Шаг при изм. t на 5С | 0,0346 | +5 | +13,60 | ||
| Округлённый шаг | 0,03 | +5 | +14,00 | ||
| Мысленные опыты | 9 | 0,73 | 140 | 44 | - |
| 10 | 0,76 | 145 | 58 | - | |
| 11 | 0,79 | 150 | 72 | 66,70 | |
| 12 | 0,82 | 155 | 86 | - | |
| 13 | 0,85 | 160 | 100 | 72,50 | |
| 14 | 0,88 | 165 | 114 | 68,40 |
Примем величину шага фактора 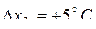 , уменьшив его по сравнению с первоначальным примерно в 10 раз. Во столько же раз следует уменьшить величину шага факторов
, уменьшив его по сравнению с первоначальным примерно в 10 раз. Во столько же раз следует уменьшить величину шага факторов 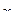 и
и 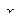 . Изменению величины шага соответствует в табл.3.13 строка "Шаг при изменении
. Изменению величины шага соответствует в табл.3.13 строка "Шаг при изменении 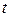 на
на 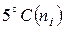 ". Прибавляя значения округлённого шага к основному уровню, получим значения факторов для мысленных опытов 9-14. Далее по уравнению регрессии рассчитываем ожидаемые значения функции отклика (опыты 11,13,14). Оказалось, что лучшие результаты достигаются в опыте 13:
". Прибавляя значения округлённого шага к основному уровню, получим значения факторов для мысленных опытов 9-14. Далее по уравнению регрессии рассчитываем ожидаемые значения функции отклика (опыты 11,13,14). Оказалось, что лучшие результаты достигаются в опыте 13: 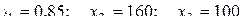 . Итак, оптимум найден.
. Итак, оптимум найден.
Поговорим теперь о принятии решений после реализации крутого восхождения. Ситуации могут быть различными (также как это было при построении модели и ее оценке). Крутое восхождение могло оказаться эффективным или нет. Положение оптимума также влияет на принятие решений. В некоторых случаях также учитывается адекватность (или неадекватность) линейной модели.
Об эффективности движения по градиенту можно судить по величине параметра оптимизации. Движение по градиенту считается эффективным, если реализация мысленных опытов, рассчитанных на стадии крутого восхождения, приводит к улучшению значения параметра оптимизации по сравнению с самым хорошим результатом в матрице. Здесь возможны два варианта:
- область оптимума достигнута – простейший вариант, здесь при необходимости детального изучения области оптимума проводятся дальнейшие исследования, но уже на нелинейных планах, по крайней мере второго порядка;
- если область оптимума не достигнута, ставится линейный план следующего цикла крутого восхождения и исследование продолжается (возможен также переход к нелинейным планам или прекращение исследований).
Если крутое восхождение неэффективно также возможно несколько вариантов.
- область оптимума близка, т.е. при реализации матрицы планирования получены достаточно хорошие результаты, которые не удалось улучшить при крутом восхождении – возможно окончание исследования или переход к нелинейным планам;
- область оптимума далека/линейная модель адекватна (крутое восхождение должно было дать результат) –возможно дело в самом характере поверхности отклика (например, она не гладкая) – следует переместиться в другую область факторного пространства и построить линейный план второго цикла крутого восхождения;
- область оптимума далека/линейная модель неадекватна; возможно, что интервалы варьирования выбраны неудачно; другой вариант – матрица построена по полуреплике или по дробной реплике: в этом случае стоит достроить матрицу планирования до полной или использовать метод “перевала”:
- положение оптимума неопределенное, т.е. если информации о положении оптимума нет и не удалось улучшить значение параметра оптимизации на стадии крутого восхождения, можно поставить опыты в центре эксперимента с целью оценки вклада квадратичных членов и при необходимости строить план второго порядка.
3.7. Метод симплекс-планирования
Симплекс - это выпуклая геометрическая фигура с числом вершин на единицу больше, чем число факторов. На плоскости симплекс имеет вид треугольника, в трёхмерном пространстве - это тетраэдр и в k-мерном пространстве фигура, имеющая k+1 вершину (фиг.3.5).
Стратегия симплекс-планирования определяется правилами, знание которых позволяет правильно записать исходный симплекс, найти координаты следующих точек при движении и перейти от симплекс-плана к планированию эксперимента, выполняемого для описания почти стационарной области.
Центр симплексов помещают в начало координат, а расстояние между его вершинами (сторону симплекса) принимают равным единице. Ориентируют симплекс в факторном пространстве таким образом, чтобы вершина 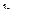 лежала на оси
лежала на оси  , а остальные вершины располагались симметрично относительно координатных осей. В этом случае координаты вершин симплексов можно определить, зная радиусы вписанной (
, а остальные вершины располагались симметрично относительно координатных осей. В этом случае координаты вершин симплексов можно определить, зная радиусы вписанной (  ) и описанной (
) и описанной ( 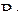 ) гипосфер.
) гипосфер.
При симплекс-планировании движение в область оптимума в факторном пространстве осуществляется перемещением симплекса путём последовательного отбрасывания его вершин, имеющих минимальное значение параметра оптимизации, и поворота симплекса вокруг грани, противоположной отброшенной вершине. Например, если в точках 1,2,3 поставлены эксперименты (фиг.3.6) и наихудшее значение параметра оптимизации оказалось в точке 1, то треугольник поворачивают вокруг стороны 2-3, в результате чего получают точку 4, в которой ставят очередной эксперимент. Из точек 2,3 и 4 выбирают наихудшую и снова делают поворот вокруг стороны, противолежащей наихудшей точке. Процедуру повторяют до тех пор, пока симплекс не начнёт вращаться вокруг точки оптимума.

Если поверхность отклика близка к линейной, то движение из центра каждого симплекса через грань, противоположную вершине с минимальным значением параметра оптимизации, совпадает по направлению с движением по градиенту, рассчитанному по результатам опытов, выполненных в вершинах симплексов.
Первая задача симплекс-планирования состоит в построении матрицы исходного симплекса, в которую записывают координаты экспериментальных точек. Матрицу исходного симплекса строят путём последовательного перехода от одного симплекса к другому, увеличивая размерность симплексов на единицу. Координаты вершин симплексов можно определить из следующей матрицы:
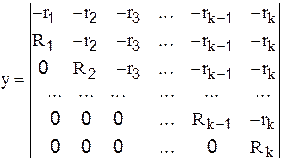 .
.
Величины радиусов для вписанной (  ) и описанной (
) и описанной ( 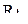 ) сфер
) сфер 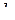 - мерного симплекса определяются формулами:
- мерного симплекса определяются формулами:
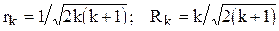 .
.
Результаты определения координат вершин симплексов для k=7 приведены в табл.3.14.
Матрицей пользоваться удобнее, если её привести к такому виду, чтобы она соответствовала симплексу с радиусом 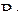 сферы, равным единице. Для этого все элементы числовой матрицы в табл.3.14 необходимо разделить на величину максимального элемента для симплекса определённой размерности.
сферы, равным единице. Для этого все элементы числовой матрицы в табл.3.14 необходимо разделить на величину максимального элемента для симплекса определённой размерности.
Для симплекса, характеризующего два фактора  , все элементы матрицы следует разделить на 0,578; при k=3 на 0,612, при k=4 на 0,632 и т.д. Деление на величину максимального элемента приводит к тому, что суммы квадратов элементов для всех столбцов становятся равными. Это условие, а также ортогональность матрицы и симметричное расположение независимых переменных относительно центра эксперимента обеспечивают оптимальность симплекс-планирования. Преобразованные оптимальные матрицы для двух и четырёх факторов приведены в табл.3.15 и 3.16.
, все элементы матрицы следует разделить на 0,578; при k=3 на 0,612, при k=4 на 0,632 и т.д. Деление на величину максимального элемента приводит к тому, что суммы квадратов элементов для всех столбцов становятся равными. Это условие, а также ортогональность матрицы и симметричное расположение независимых переменных относительно центра эксперимента обеспечивают оптимальность симплекс-планирования. Преобразованные оптимальные матрицы для двух и четырёх факторов приведены в табл.3.15 и 3.16.
Таблица 3.14
Численные значения координат вершин симплекса для k=7
| № опыта | 
| 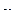
| 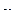
| 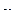
| 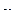
| 
| 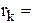 
| отклик |
| 1 | -0,500 | -0,289 | -0,204 | -0,158 | -0,129 | -0,109 | -0,0945 | 
|
| 2 | 0,500 | -0,289 | -0,204 | -0,158 | -0,129 | -0,109 | -0,0945 | 
|
| 3 | 0 | 0,578 | -0,204 | -0,158 | -0,129 | -0,109 | -0,0945 | 
|
| 4 | 0 | 0 | 0,612 | -0,158 | -0,129 | -0,109 | -0,0945 | 
|
| 5 | 0 | 0 | 0 | 0,632 | -0,129 | -0,109 | -0,0945 | 
|
| 6 | 0 | 0 | 0 | 0 | 0,645 | -0,109 | -0,0945 | 
|
| 7 | 0 | 0 | 0 | 0 | 0 | 0,654 | -0,0945 | 
|
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0,662 | 
|
Таблица 3.15
Матрица симплекс-планирования для двух факторов
| № опытов в исходном симплексе | Факторы

|

| Отклик |
| 1 | -0,865 | -0,500 | 
|
| 2 | +0,865 | -0,500 | 
|
| 3 | 0 | 1 | 
|
Таблица 3.16
Матрица симплекс-планирования для четырёх факторов
| № опытов в исходном симплексе | 
| 
| 
| 
| отклик |
| 1 | -0,790 | -0,457 | -0,323 | -0,250 | 
|
| 2 | 0,790 | -0,457 | -0,323 | -0,250 | 
|
| 3 | 0 | 0,914 | -0,323 | -0,250 | 
|
| 4 | 0 | 0 | 0,969 | -0,250 | 
|
| 5 | 0 | 0 | 0 | 1,0 | 
|
После построения матрицы исходного симплекса решается вторая задача симплекс-планирования, а именно, движение в область оптимума.
Перемещение симплекса в факторном пространстве осуществляется путём его поворота вокруг грани, противоположной вершине с минимальным значением параметра оптимизации. Координаты новой вершины следующие:
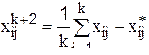 ,
,
где 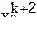 - координаты новой точки;
- координаты новой точки; 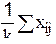 - среднее из координат всех точек симплекса, кроме "плохой";
- среднее из координат всех точек симплекса, кроме "плохой"; 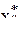 - координата "плохой" точки. После построения нового симплекса и проведения опытов в найденной точке вновь решается вопрос о том, какая из точек может быть исключена. Последовательное отображение различных величин симплекса приводит к тому, что центр симплекса перемещается по некоторой ломанной линии. Траектория его движения зависит от порядка, в котором отображаются вершины симплекса. Центр симплекса движется с максимальной скоростью, если порядок отображения вершин соответствует периодически повторяющемуся ряду всех вершин (фиг.3.7). Незакономерная последовательность отображения вершин (некоторые вершины отображаются чаще остальных) замедляет движение центра симплекса.
- координата "плохой" точки. После построения нового симплекса и проведения опытов в найденной точке вновь решается вопрос о том, какая из точек может быть исключена. Последовательное отображение различных величин симплекса приводит к тому, что центр симплекса перемещается по некоторой ломанной линии. Траектория его движения зависит от порядка, в котором отображаются вершины симплекса. Центр симплекса движется с максимальной скоростью, если порядок отображения вершин соответствует периодически повторяющемуся ряду всех вершин (фиг.3.7). Незакономерная последовательность отображения вершин (некоторые вершины отображаются чаще остальных) замедляет движение центра симплекса.

При перемещении симплекса в факторном пространстве может возникнуть ситуация, при которой в новой точке величина параметра оптимизации будет минимальной (как в предшествующей точке). При отбрасывании этой точки происходит возврат к исходному симплексу, а далее симплексы начинают колебаться относительно одной грани. такое возможно, если вершины симплекса располагаются на гребне поверхности отклика. В этом случае рекомендуется уменьшить длину грани симплекса и эксперименты повторить.
При движении симплекса в факторном пространстве может наступить его вращение вокруг одной из вершин - зацикливание симплекса (фиг.3.7). Это свидетельствует о том, что в результате движения достигнута область оптимума. Следует иметь в виду, что причиной зацикливания симплекса может быть и ошибка эксперимента.
Симплекс-планирование является одним из эффективных методов поиска оптимальной области. Метод обладает многими достоинствами: прост для вычислений; не предъявляется особых требований к точности эксперимента (наихудшую ситуацию можно определить приближённо); обеспечивается высокая эффективность при минимальном числе экспериментов. Симплекс-планирование относится к методам, которые можно успешно использовать в промышленных условиях.
Пример. Рассмотрим движение к оптимальной области методом симплекс-планирования. Допустим, что натуральные значения нулевого уровня и интервал варьирования двухфакторного симплекс-плана заданы табл.3.17. Тогда формулы перехода от натуральных к безразмерным факторам в соответствии с методом кодирования примут вид: 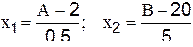 . Откуда
. Откуда 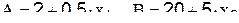 .
.
Подставляя в полученные уравнения значения 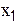 и
и  из табл. 3.15 и произведя вычисления, получим рабочую матрицу с натуральными значениями факторов (табл.3.18).
из табл. 3.15 и произведя вычисления, получим рабочую матрицу с натуральными значениями факторов (табл.3.18).
Таблица 3.17
Натуральные значения факторов
| Факторы | Нулевой уровень | Интервал варьирования |
| А | 2,0 | 0,5 |
| В | 20 | 5 |
Таблица 3.18
Матрица симплекс-планирования в натуральных значениях факторов
| № опытов | Факторы | Отклик | |
| А | В | ||
| 1 | 1,57 | 17,5 | 
|
| 2 | 2,43 | 17,5 | 
|
| 3 | 2,0 | 25,0 | 
|
Координаты новых точек найдём по формуле 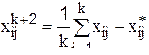 .
.
Значения факторов определяем из табл. 3.17.
Для А 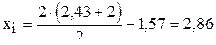 ; для В
; для В 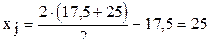 .
.
Аналогичные результаты можно получить следующим путём. Для фактора 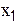 средняя координата "хороших" точек равна
средняя координата "хороших" точек равна  . Величина "плохой" точки - 1,57. Чтобы найти новую точку будем двигаться от "плохой" точки до средней координаты "хороших" точек, т.е. на величину 2,215-1,57=0,645, и дополнительно на такое же расстояние за грань симплексов, противоположную "плохой" точке. Тогда новая координата будет 1,57+0,645+0,645=2,86. Такое же значение было получено выше путём расчёта по приведенной формуле.
. Величина "плохой" точки - 1,57. Чтобы найти новую точку будем двигаться от "плохой" точки до средней координаты "хороших" точек, т.е. на величину 2,215-1,57=0,645, и дополнительно на такое же расстояние за грань симплексов, противоположную "плохой" точке. Тогда новая координата будет 1,57+0,645+0,645=2,86. Такое же значение было получено выше путём расчёта по приведенной формуле.
3.8. Критериальное планирование эксперимента
В результате эксперимента необходимо получить максимальный объём данных об объекте исследования при наибольшей точности и наименьших затратах. Эффективным способом достижения этой цели является приведение переменных, характеризующих состояние объекта, к безразмерному виду и уменьшение набора переменных.
При фактическом написании уравнений и в конкретных числовых расчетах необходимо вводить и использовать различные системы координат. Эти системы могут быть произвольными, однако, во многих случаях они выбираются из соображений простоты и удобства вычислений или анализа численных расчетов. Возможный произвол в выборе системы координат не связан с существом самих явлений, поэтому различные физические уравнения должны обладать свойством инвариантности относительно выбора системы координат. Именно в этом состоит причина того, что множество характеристик движения и состояния имеет инвариантную тензорную природу. С другой стороны, определение и задание различных величин (характеристик среды, поля, процессов, например плотности, энергии, скорости) в численном представлении связано с использованием определенных единиц измерения, выбор которых зависит от исследователя.
Величины, численное значение которых в рассматриваемых вопросах зависит от выбора единиц измерения, называются размерными величинами. Пример – энергия (джоули, калории, рубли).
Действия с большим числом разнообразных характеристик, связанных между собой различными определениями и различными уравнениями, показывают, что единицы измерения для разных характеристик, вообще говоря, связаны между собой. Например, единица измерения для скорости связана с единицами измерения для длины и времени. В данном случае мы имеем зависимую единицу измерения.
Наряду с зависимыми единицами измерения существуют первичные, независимые единицы измерения (базис), в частности, длины, времени, массы. Эти величины вводятся опытным путем, с помощью специальных теоретических и, вообще говоря, произвольных условий. Например, в системе единиц измерения СИ базисом или основными единицами измерения являются метр, килограмм-масса, секунда, ампер, градус Кельвина. Величины, для которых единицы измерения вводятся из опыта, с помощью эталонов, по условию называются первичными или основными. При этом сами единицы измерения также называются первичными или основными. Единицы измерения для других величин, которые получаются из определения этих величин через первичные, называются производными или вторичными единицами измерения.
Выражение производной единицы измерения через основные единицы измерения называется размерностью. Размерность записывается в виде формулы. Например, символ единицы измерения для силы записывается в форме: 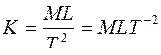 . Формулы размерности позволяют определить численные масштабные множители для пересчета соответствующих характеристик при изменении величин первичных единиц измерения.
. Формулы размерности позволяют определить численные масштабные множители для пересчета соответствующих характеристик при изменении величин первичных единиц измерения.
Сколько может быть первичных единиц измерения? Мы рассмотрели пример с тремя первичными единицами измерения. В уравнениях газовой динамики сюда добавляется также единица измерения температуры, а для количества тепловой энергии, например, калория. В этих случаях формулы для определения размерностей будут представлять собой степенные одночлены вида, указанного выше.
Можно вводить системы единиц измерения, вообще говоря, с любым числом первичных единиц. Например, для длины, времени и скорости можно ввести независимые единицы измерения из опыта, но в этом случае формулу для скорости следует писать в виде: 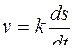 , где
, где 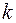 - размерная постоянная, зависящая от выбора единиц измерения для
- размерная постоянная, зависящая от выбора единиц измерения для 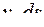 и
и 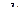 . Если принять, что
. Если принять, что 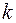 является абсолютной численной постоянной (равной или не равной единице), то в любой системе единиц измерения единицы измерения для
является абсолютной численной постоянной (равной или не равной единице), то в любой системе единиц измерения единицы измерения для 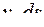 и
и 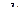 будут зависимы, что обычно и принимается на практике. Наоборот, если зафиксировать, например, размерную универсальную постоянную в законе всемирного тяготения,
будут зависимы, что обычно и принимается на практике. Наоборот, если зафиксировать, например, размерную универсальную постоянную в законе всемирного тяготения, 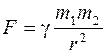 , получится дополнительная связь между единицами измерения для массы, времени и расстояния. Таким путем можно получать системы единиц измерения с различным числом первичных единиц. Например, можно ввести систему с универсальными единицами измерения, в которой единицы измерения всех величин раз и навсегда фиксированы и поэтому все величины можно рассматривать как безразмерные.
, получится дополнительная связь между единицами измерения для массы, времени и расстояния. Таким путем можно получать системы единиц измерения с различным числом первичных единиц. Например, можно ввести систему с универсальными единицами измерения, в которой единицы измерения всех величин раз и навсегда фиксированы и поэтому все величины можно рассматривать как безразмерные.
Понятия размерных и безразмерных величин относительны. При рассмотрении данного явления вводятся различные переменные или постоянные характеристики процессов и объектов. Для получения численных значений явно или неявно используется в действительности ли потенциально допускается совокупность систем единиц измерения.
Величины, численное значение которых зависит от выбора конкретной системы единиц измерения, называются размерными. Величины, численное значение которых неизменно для всей совокупности систем единиц измерения (для рассматриваемого случая), называются безразмерными или отвлеченными. Например, измерение углов – если ограничиться только системами, где углы измеряются только в радианах. Допустим, примем такое же допущение и о единицах длины. На практике первое допущение нормально, а второе – неудобно, поскольку для геометрически подобных систем соответственные углы одинаковы, а длины различны.
Иногда прослеживается тенденция к стандартизации, введению универсальной системы единиц измерения. Однако, иногда привязывание универсальной системы единиц измерения к определенным физическим постоянным или условиям является искусственным. Сама возможность использования произвольных единиц измерения может служить источником полезных выводов. Аналогия – выбор системы координат.
Рассмотрим теперь структуру функциональных зависимостей между вообще размерными величинами, выражающих собой физические закономерности, инвариантные относительно выбора системы единиц измерения.
Теорема. Если какое-либо уравнение однородно относительно размерностей, то его можно преобразовать к соотношению, содержащему набор безразмерных величин. Однородными относительно размерностей являются уравнения, форма которых не зависит от выбора основных единиц.
Пусть мы имеем некоторую размерную или безразмерную величину q, которая является функцией независимых между собой, вообще размерных величин:
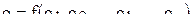 .
.
Отметим в аргументах f все размерные и безразмерные постоянные или переменные величины, от которых зависит q.
Будем полагать, что функция f выражает собой некоторый физический закон, не зависящий от выбора системы единиц измерения. Среди размерных величин  первые k величин имеют независимые размерности. Например, размерности длины L, времени
первые k величин имеют независимые размерности. Например, размерности длины L, времени 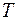 и массы
и массы 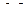 независимы; размерности длины L, скорости
независимы; размерности длины L, скорости 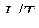 и ускорения
и ускорения 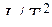 зависимы.
зависимы.
Теорема Букингема (П-теорема ) утверждает: если размерная величина q является функцией независимых между собой размерных величин 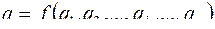 , причём среди размерных величин
, причём среди размерных величин 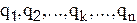 k величин (kn) имеют основные или независимые размерности, то эта функциональная зависимость может быть представлена в виде
k величин (kn) имеют основные или независимые размерности, то эта функциональная зависимость может быть представлена в виде
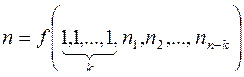 ,
,
где П и все аргументы функции f безразмерные.
Таким образом, связь f, не зависящая от выбора системы единиц измерения, между n+1 размерными величинами q,  , из которых k имеют независимые размерности, может быть представлена в виде соотношения между n+1-k величинами
, из которых k имеют независимые размерности, может быть представлена в виде соотношения между n+1-k величинами 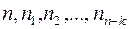 , представляющими собой безразмерные комбинации из n+1 размерных величин.
, представляющими собой безразмерные комбинации из n+1 размерных величин.
Всякое физическое соотношение между размерными величинами можно представить в безразмерном виде. В этом и заключается источник полезных приложений метода теории размерности.
Рассмотрим простейший пример: задачу об определении аналитической связи между путем, проходимым свободно падающим телом 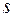 , временем падения
, временем падения 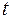 и другими факторами. Галилеем экспериментально доказано, что
и другими факторами. Галилеем экспериментально доказано, что 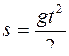 . Если экспериментально определять указанную зависимость, необходимо было бы определить факторы, от которых зависит
. Если экспериментально определять указанную зависимость, необходимо было бы определить факторы, от которых зависит 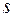 , затем организовать серию экспериментов с фиксацией изменения
, затем организовать серию экспериментов с фиксацией изменения 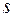 и далее аппроксимировать полученные данные некоторой зависимостью.
и далее аппроксимировать полученные данные некоторой зависимостью.
Попробуем решить эту задачу методом размерностей. Будем полагать, что 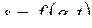 . Вид этой функции можно определить, фиксируя параметры
. Вид этой функции можно определить, фиксируя параметры 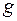 и
и 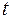 , и проведя соответствующее количество опытов. Воспользуемся
, и проведя соответствующее количество опытов. Воспользуемся 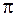 - теоремой. Размерности:
- теоремой. Размерности: 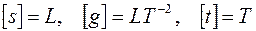 . В нашем случае
. В нашем случае  . Согласно
. Согласно 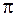 - теореме
- теореме 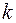 - число независимых размерностей под знаком функции. Размерности
- число независимых размерностей под знаком функции. Размерности 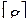 и
и 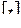 независимы, нельзя одну из них выразить через другую. Тогда
независимы, нельзя одну из них выразить через другую. Тогда  и согласно
и согласно 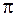 - теореме получаем, что
- теореме получаем, что 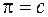 . Тогда в безразмерных величинах
. Тогда в безразмерных величинах 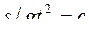 или
или 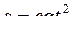 и достаточно всего одного опыта, где зарегистрированы
и достаточно всего одного опыта, где зарегистрированы 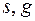 и
и 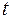 .
.
Пример. Требуется ввести фундаментальную систему параметров П для тяжёлой несжимаемой вязкой жидкости.
Р е ш е н и е. Этап 1. Выбираем независимые переменные, характеризующие состояние тяжёлой вязкой несжимаемой жидкости. К ним относятся геометрические параметры (или координаты) 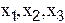 , время t, скорости
, время t, скорости 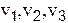 , ускорение свободного падения g, плотность , вязкость , давление р.
, ускорение свободного падения g, плотность , вязкость , давление р.
Этап 2. Выбираем систему основных размерностей, через которые выражаем единицы измерения всех основных переменных. Имеем
 ,
,
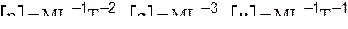 .
.
Этап 3. Составим матрицу размерностей выбранных независимых переменных и безразмерные комбинации:
| M | L | T | |
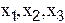
| 0 | 1 | 0 |
| t | 0 | 0 | 1 |
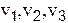
| 0 | 1 | -1 |
| p | 1 | -1 | -2 |
| g | 0 | 1 | -2 |
| 1 | -3 | 0 | |
| 1 | -1 | -1 |
Ранг матрицы r=3, число размерных, определяющих движение величин n=7. Фундаментальная система параметров П содержит 7-3=4 параметра. Они соответствую известным в гидродинамике следующим числам (критериям) подобия: 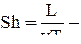 число Струхала, Eu=
число Струхала, Eu= 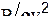 - число Эйлера (здесь Р - сила, давление); Re=
- число Эйлера (здесь Р - сила, давление); Re= 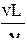 - число Рейнольдса (здесь - кинематическая вязкость); Fr=
- число Рейнольдса (здесь - кинематическая вязкость); Fr= 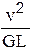 - число Фруда (G - объёмные силы).
- число Фруда (G - объёмные силы).
Этап 4. Осуществляем изучение полученных комбинаций с точки зрения их физического смысла. Это изучение показывает целесообразность применения введенных безразмерных величин;
Этап 5. Здесь можно приступить к планированию эксперимента с использованием полученных безразмерных комплексов.
Пример. Молот преобразует потенциальную энергию U массы падающих частей Q с высоты Н в кинетическую энергию Е, которая расходуется на пластическую деформацию заготовки V (высота h заготовки уменьшается на величину 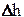 ). Необходимо правильно выбрать параметры молота Q и Н.
). Необходимо правильно выбрать параметры молота Q и Н.
Р е ш е н и е. Искомая потенциальная энергия U=QH зависит от размеров и параметров материала заготовки следующим образом
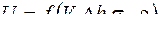 ,
,
где 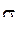 - предел текучести при растяжении; - массовая плотность.
- предел текучести при растяжении; - массовая плотность.
Размерности величин, входящих в функцию f следующие:
[U]= 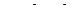 ;[V]=
;[V]= 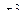 ;
; 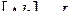 ;
; 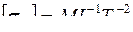 ;
; 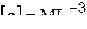 .
.
Из четырёх аргументов 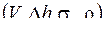 три имеют независимые размерности:
три имеют независимые размерности: 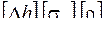 . Чтобы убедиться в этом, предположим, что эти размерности зависимы. Это означает, что из двух размерностей, возводя их в степени ,, можно получить третью, т.е. можно предположить, что
. Чтобы убедиться в этом, предположим, что эти размерности зависимы. Это означает, что из двух размерностей, возводя их в степени ,, можно получить третью, т.е. можно предположить, что 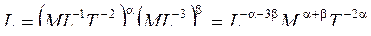 . Из последнего имеем три уравнения: 1=--3; 0=+; 0=-2. Решения приведенной системы уравнений не существует, следовательно, первоначальная гипотеза не подтверждается.
. Из последнего имеем три уравнения: 1=--3; 0=+; 0=-2. Решения приведенной системы уравнений не существует, следовательно, первоначальная гипотеза не подтверждается.
Аналогично можно показать, что размерность [V] зависит от упомянутых выше размерностей. Для этого необходимо составить выражение типа: 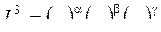 . Поступая аналогично предыдущему, доказываем принятую гипотезу.
. Поступая аналогично предыдущему, доказываем принятую гипотезу.
Согласно П-теореме зависимость 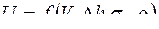 можно представить так (n=4; k=3):
можно представить так (n=4; k=3): 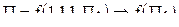 .
.
Составим безразмерные величины П и 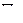 :
:
П= 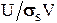 ;
; 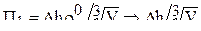 .
.
Величины Q,H связаны для процесса ковки на молотах зависимостью:
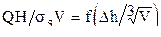 .
.
Таким образом, от исследования функции четырёх аргументов перешли к исследованию функции одного аргумента.
Существующие методы моделирования основываются на теории подобия, которая основывается на трёх теоремах, устанавливающих критерии подобия. Критерии подобия составляются из заданных параметров объекта исследования и независимых параметров процесса (например, времени). Таким образом, для математической формулировки условий, при которых модель отражает изучаемый объект используют теорию подобия, в которой устанавливаются критерии подобия модели и оригинала.
При моделирования физических явлений необходимо учитывать:
· факторы, обусловливающие расхождение результатов, получаемых в модели и оригинале: погрешности определения отдельных параметров, входящих в критерии подобия;
· неточности исходного математического описания явления; погрешности получения критериев подобия за счёт упрощенного представления явления при его изучении;
· случайного отклонения параметров оригинала и модели (полученных в результате вычислений);
· погрешности проведения опытов, отклонение фактических параметров режима от расчётных и т.д.;
· погрешности обработки результатов опытов.
Все перечисленные факторы действуют как в модели, так и в оригинале - объекте исследования.
В соответствии с теорией подобия процессы будут подобными друг другу, если существует некоторое соответствие сходственных величин (рассматриваемых в некоторой системе координат) объектов: положения точек, геометрических размеров, параметров объектов и параметров процессов. В частности, две геометрические фигуры называют подобными, если отношения длин всех их сходственных отрезков одинаковы и если, осуществляя мысленное однородное растяжение или сжатие по всем координатным направлениям фигур, они совпадут при наложении друг с другом вместе со своими сходственными отрезками. Далее предполагаем, что физическое подобие является обобщением геометрического подобия и физически подобные объекты обязательно подобны друг другу геометрически.
Обычно соотношение подобия имеет вид: 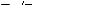 , где
, где 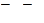 - сходственные параметры;
- сходственные параметры;  -ый коэффициент подобия или масштаб.
-ый коэффициент подобия или масштаб.
Абсолютное подобие - это тождество явлений в пространстве и во времени, получаемое после соответствующего изменения масштаба. Такое подобие для сложных объектов невозможно реализовать. Поэтому в теории подобия используется понятие полного подобия и допускается использование в некоторых случаях не полного подобия.
Полное подобие - подобие протекания во времени в пространстве основных процессов, характеризующих объект исследования.
Первая теорема подобия (о существовании критериев подобия). У явлений, подобных в том или ином смысле (математически, физически и т.д.) можно найти сочетания параметров, представляющих собой безразмерные комбинации различных величин, называемых критериями подобия, имеющими одинаковые (численно или по функциональным проявлениям) значения. Справедливо и обратное утверждение: если критерии подобия  численно одинаковы, то явления (объект и оригинал) подобны.
численно одинаковы, то явления (объект и оригинал) подобны.
В качестве примера рассмотрим случай подобных процессов, описываемых однородными уравнениями
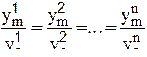 или
или 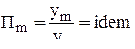 ,
,
где 1, 2, ... ,n - номера процесса;  - параметры модели и объекта; П - критерии подобия. Здесь idem означает соответственно одинаково для всех рассмотренных процессов.
- параметры модели и объекта; П - критерии подобия. Здесь idem означает соответственно одинаково для всех рассмотренных процессов.
Заметим, что критерии подобия могут преобразовываться в критерии другой формы с использованием операций их перемножения.
Вторая теорема подобия (П-теорема). Всякое полное уравнение физического процесса, записанное в определённой системе единиц, может быть представлено в виде зависимости между безразмерными соотношениями из входящих в уравнения параметров, которые и есть критерии подобия.
Теорема указывает на возможность замены переменных и сокращения их числа с m размерными до n безразмерных величин. Весьма существенно, что переход к безразмерным соотношениям позволяет распространить результаты исследования, проведенные применительно к конкретному процессу, на ряд подобных процессов.
Третья теорема подобия. Необходимыми и достаточными условиями подобия является пропорциональность сходственных параметров и равенство критериев подобия изучаемого явления.
Все условия подобия, относящиеся к детерминированно-заданным системам, справедливы для стохастически определённых систем при условии совпадения у этих систем плотностей вероятностей сходственных параметров, представленных в виде относительных характеристик. При этом дисперсии и математические ожидания всех параметров с учётом масштабов должны быть у подобных систем одинаковыми.
Способы определения критериев подобия:
1) приведение уравнений процесса к безразмерному виду (здесь необходимо иметь математическую модель процесса);
2) применение П-теоремы (здесь можно обойтись без математической модели, если известны параметры процесса);
3) все параметры выражаются в долях от определённым образом выбранных базисных величин.
Пример. Рассмотрим применение первого способа определения критериев подобия для случая вынужденных механических колебаний с демпфированием. Пусть груз массой М колеблется на пружине жёсткостью с, причём при перемещении его на расстояние l в вязкой среде появляется сила сопротивления 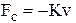 , пропорциональная скорости v. На груз действует возмущающая сила
, пропорциональная скорости v. На груз действует возмущающая сила 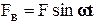 . дифференциальное уравнение имеет вид
. дифференциальное уравнение имеет вид
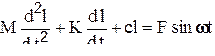 .
.
Для получения критериев подобия достаточно разделить все слагаемые уравнения на первый член. Тогда имеем:
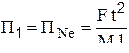 - критерий Ньютона;
- критерий Ньютона; 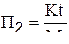 ;
; 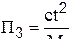
и дополнительный критерий 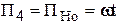 - критерий гомохронности.
- критерий гомохронности.
Роль критериев подобия следующая. Во-первых, с их помощью определяются масштабы, связывающие параметры модели и оригинала; во-вторых, на основе анализа критериальных соотношений выявляются характерные свойства моделируемого явления. В связи с этим определению критериев подобия уделяют значительное внимание.
Некоторые критерии механического подобия даны в приложении.
Физическое моделирование - это воспроизведение некоторого реального объекта - натуры с помощью устройства - модели, действие которого основано на тех же физических принципах, что и натуры, с целью изучения закономерностей на модели и перенесения полученных результатов на натуру. Модели проще и дешевле натуры; они отличаются от натуры второстепенными деталями, например они могут быть значительно меньше натуры, но при этом основные физические принципы работы модели и натуры должны быть одинаковыми.
Процесс пластической деформации металла в общем виде описывается системой уравнений, в которую входят: дифференциальные уравнения траекторий материальных точек (частиц); кинематические соотношения (связывают скорости перемещений частиц 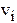 с компонентами тензора скоростей деформаций
с компонентами тензора скоростей деформаций 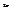 ); уравнения совместности деформаций; дифференциальные уравнения движения (или равновесия); физические уравнения связи компонент тензора напряжений
); уравнения совместности деформаций; дифференциальные уравнения движения (или равновесия); физические уравнения связи компонент тензора напряжений  с компонентами тензора скорости деформаций; термодинамические соотношения, в числе которых уравнение теплопроводности; соответствующие начальные и граничные условия.
с компонентами тензора скорости деформаций; термодинамические соотношения, в числе которых уравнение теплопроводности; соответствующие начальные и граничные условия.
Будем полагать, что систему уравнений механики пластического формоизменения можно решить, например, относительно поля скоростей или поля напряжений 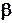 . Чтобы записать такой результат в критериальной форме все параметры, фигурирующие в исходной системе уравнений, приводятся к безразмерному виду. Согласно [6]:
. Чтобы записать такой результат в критериальной форме все параметры, фигурирующие в исходной системе уравнений, приводятся к безразмерному виду. Согласно [6]:
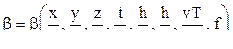 ,
,
где l, b, h - характерные размеры тела; T - время соответствующее окончанию процесса; v - скорость инструмента; f - коэффициент, характеризующий контактное трение.
Пластически деформируемые тела называют подобными друг другу, если они геометрически подобны в любой сходственный момент времени и если во всех их сходственных точках в любой сходственный момент времени безразмерные механические переменные одинаковы.
Для того, чтобы осуществить модельный эксперимент по горячей деформации металла, необходимо подобрать следующие условия опыта: модель должна быть геометрически подобна натуре, критерии подобия должны быть выполнены.
Теория планирования эксперимента и теория подобия, способствующие наилучшей организации эксперимента и обработке его результатов, в настоящее время применяются совместно.
Пусть, например, требуется изучить зависимость 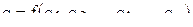 , которая связывает целевую функцию эксперимента (какое-либо экспериментальное значение параметра) со значениями других параметров. В этом случае для критериального планирования эксперимента необходимо:
, которая связывает целевую функцию эксперимента (какое-либо экспериментальное значение параметра) со значениями других параметров. В этом случае для критериального планирования эксперимента необходимо:
1) определение вида безразмерных комплексов  и критериальной целевой функции (если дифференциальные уравнения процесса известны, следует преобразовать эти уравнения и начальные (граничные) условия и привести их к критериальному виду в соответствии с описанным выше способом;
и критериальной целевой функции (если дифференциальные уравнения процесса известны, следует преобразовать эти уравнения и начальные (граничные) условия и привести их к критериальному виду в соответствии с описанным выше способом;
2) определение диапазонов варьирования безразмерных комплексов по заданным интервалам варьирования параметров;
3) выявление доминирующих безразмерных комплексов из  путём проведения отсеивающего эксперимента;
путём проведения отсеивающего эксперимента;
4) проведение опытов (расчётов) в соответствии с матрицей критериального планирования активного или пассивного эксперимента с целью определения коэффициентов уравнения регрессии:
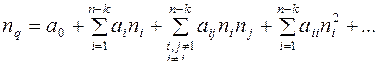
Если эксперименты проводятся в реальной системе или на физической модели, в матрицу критериального планирования эксперимента, содержащую в качестве варьируемых факторов безразмерные комплексы, необходимо ввести ещё значения варьируемых параметров.
Полученное в результате проведения минимума опытов (расчётов) уравнение регрессии, связывающее безразмерные комплексы, позволяет не только изучить конкретную зависимость, но и распространить результаты опытов на широкий класс процессов.
О классификации экспериментальных планов.
В зависимости от задачи исследования, свойств объекта, выполнения заданных математических предпосылок, наличия априорной информации и т.д. можно выбрать тот или иной класс планов для получения необходимой информации.
В виде предварительной классификации можно составить следующую схему:
· планы дисперсионного анализа;
· планы отсеивающего эксперимента;
· планы многофакторного анализа;
· планы для изучения поверхности отклика;
· планы для динамических задач планирования;
· планы для изучения механизма явлений;
· планы для построения диаграмм состав – свойство, состав – состояние.
Все перечисленные планы можно объединить в три группы:
· планы дисперсионного анализа;
· планы регрессионного анализа;
· планы ковариационного анализа.
Заметим, что границы между указанными видами анализа не являются общепризнанными и очевидными, тем не менее, приведенная выше классификация полезна и целесообразна.
1. Дисперсионный анализ – это статистический метод, с помощью которого производится разложение суммарной дисперсии на составляющие. В зависимости от числа источников дисперсии бывает однофакторный и многофакторный. Если при постановке опытов реализуются все возможные совокупности условий, имеем полную классификацию дисперсионного анализа. Если реализуется только часть – классификация неполная. Сокращение вариантов может происходить случайным образом или строго по правилам (без ограничения на рандомизацию и с ограничением). Полные классификации обычно применяются для небольшого числа факторов (не более 5). Число уровней может быть как одинаковым для всех факторов, так и различным. Модель выглядит следующим образом: 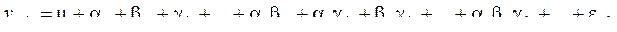 где
где 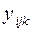 - результат эксперимента на
- результат эксперимента на 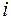 - м уровне первого фактора,
- м уровне первого фактора, 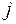 - м уровне второго фактора…;
- м уровне второго фактора…; 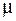 - среднее по всем опытам,
- среднее по всем опытам, 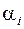 - эффект
- эффект 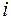 - го уровня первого фактора и т.д.;
- го уровня первого фактора и т.д.; 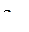 - остаточный член для оценки ошибки эксперимента.
- остаточный член для оценки ошибки эксперимента.
2. Планы многофакторного анализа используются при оценке эффектов взаимодействия многих факторов, варьируемых на одинаковом (симметричные планы) или неодинаковом (несимметричные планы) числе уровней. Общее уравнение модели: 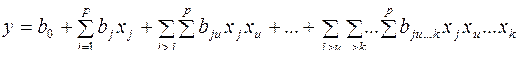 Наиболее распространены симметричные двухуровневые планы типа
Наиболее распространены симметричные двухуровневые планы типа 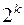 (возможны полные планы и дробные реплики). Могут быть также многоуровневые симметричные планы и многоуровневые несимметричные планы (факторы варьируются на различных уровнях, строятся различными способами, например, комбинированием полных и дробных планов типа
(возможны полные планы и дробные реплики). Могут быть также многоуровневые симметричные планы и многоуровневые несимметричные планы (факторы варьируются на различных уровнях, строятся различными способами, например, комбинированием полных и дробных планов типа 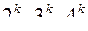 .
.
3. Планы для изучения поверхности отклика применяются для детального изучения области оптимума и участков поверхности отклика со значительной кривизной, там где линейная модель неадекватна. Обычно бывает достаточно планов второго порядка, реже используются планы третьего порядка. Например, для плана второго порядка: 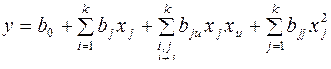 . Если часть эффектов отсутствует, используют планы типа плана Хартли (если нет некоторых линейных или парных эффектов), строящиеся на основе минимальных регулярных реплик где должны быть не смешаны между собой только парные эффекты. Планы третьего порядка применяют редко и обычно строят последовательно на базе планов первого и второго порядка.
. Если часть эффектов отсутствует, используют планы типа плана Хартли (если нет некоторых линейных или парных эффектов), строящиеся на основе минимальных регулярных реплик где должны быть не смешаны между собой только парные эффекты. Планы третьего порядка применяют редко и обычно строят последовательно на базе планов первого и второго порядка.
4. Планы отсеивающего эксперимента используют на стадии предварительных исследований для выделения существенных эффектов факторов.
ЛИТЕРАТУРА
1. Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 1972. - 368 с.
2. Веников В.А. Теория подобия и моделирования. М.: Высшая школа, 1976. - 479 с.
3. Адлер Ю.П., Маркова Е.В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий. - М.: Наука, 1976. -279 с.
4. Шенк Х. Теория инженерного эксперимента. - М.: Мир, 1972. - 381 с.;
5. Новик Ф.С., Арсов Я.Б. Оптимизация процессов технологии металлов методами планирования экспериментов. М.: Машиностроение, 1980.
6. Колмогоров В.Л. Механика обработки металлов давлением. М.: 1986. - 688 с.
7. Лель Р.В. Статистическая обработка и планирование экспериментов в технологии машиностроения. Учебное пособие. - Горький: Горьковский гос. университет. 1979. - 67 с.
8. Линник Ю.В. Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений. М.: Физматгиз. 1962.
9. Налимов В.В., Чернова Н.А. Статистические методы планирования экстремальных экспериментов. М.: Наука, 1965.
ПРИЛОЖЕНИЕ
Таблица 1
Таблица значений функции Лапласа Ф(х)
| х | Ф(х) | х | Ф(х) | х | Ф(х) | х | Ф(х) |
| 0,0 | 0,0000 | 1,0 | 0,3413 | 2,0 | 0,4772 | 3,0 | 0,4986 |
| 0,1 | 0,0398 | 1,1 | 0,3643 | 2,1 | 0,4821 | 3,1 | |
| 0,2 | 0,0793 | 1,2 | 0,3849 | 2,2 | 0,4861 | 3,2 | 0,4993 |
| 0,3 | 0,1179 | 1,3 | 0,4032 | 2,3 | 0,4893 | 3,3 | |
| 0,4 | 0,1554 | 1,4 | 0,4192 | 2,4 | 0,4918 | 3,4 | 0,4996 |
| 0,5 | 0,1915 | 1,5 | 0,4332 | 2,5 | 0,4938 | 3,5 | |
| 0,6 | 0,2257 | 1,6 | 0,4452 | 2,6 | 0,4953 | 3,6 | 0,4998 |
| 0,7 | 0,2580 | 1,7 | 0,4554 | 2,7 | 0,4965 | 3,7 | |
| 0,8 | 0,2881 | 1,8 | 0,4641 | 2,8 | 0,4974 | 3,8 | 0,4999 |
| 0,9 | 0,3159 | 1,9 | 0,4713 | 2,9 | 0,4971 | 5,0 | 0,4999 |
Таблица 2
Критические точки распределения Пирсона 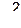
| Число степе- | Уровень значимости | ||||||
| ней свободы | 0,99 | 0,98 | 0,95 | 0,90 | 0,05 | 0,025 | 0,01 |
| 1 | 0,00016 | 0,0006 | 0,0039 | 0,016 | 0,039 | 0,001 | 0,000 |
| 2 | 0,020 | 0,040 | 0,103 | 0,211 | 0,103 | 0,051 | 0,020 |
| 3 | 0,115 | 0,185 | 0,352 | 0,584 | 0,352 | 0,216 | 0,115 |
| 4 | 0,297 | 0,43 | 0,71 | 1,06 | 0,711 | 0,484 | 0,297 |
| 5 | 0,554 | 0,75 | 1,14 | 1,61 | 1,15 | 0,831 | 0,554 |
| 6 | 0,872 | 1,13 | 1,63 | 2,20 | 1,64 | 1,24 | 0,872 |
| 7 | 1,24 | 1,56 | 2,17 | 2,83 | 2,17 | 1,69 | 1,24 |
| 8 | 1,65 | 2,03 | 2,73 | 3,49 | 2,73 | 2,18 | 1,65 |
| 9 | 2,09 | 2,53 | 3,32 | 4,17 | 3,33 | 2,70 | 2,09 |
| 10 | 2,56 | 3,06 | 3,94 | 4,86 | 3,94 | 3,25 | 2,56 |
| 11 | 3,05 | 3,6 | 4,6 | 5,6 | 4,57 | 3,82 | 3,05 |
| 12 | 3,57 | 4,2 | 5,2 | 6,3 | 5,23 | 4,40 | 3,57 |
Таблица 3
Значения критерия Кохрена для уровня значимости 0,05
| f m | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 2 | 0,9985 | 0,9750 | 0,9392 | 0,9057 | 0,8772 | 0,8534 | 0,8332 | 0,8159 |
| 3 | 0,9689 | 0,8709 | 0,7977 | 0,7457 | 0,7071 | 0,6771 | 0,6530 | 0,6333 |
| 4 | 0,9065 | 0,7679 | 0,6841 | 0,6287 | 0,5895 | 0,5598 | 0,5365 | 0,5175 |
| 5 | 0,8412 | 0,6838 | 0,5981 | 0,5441 | 0,5665 | 0,4783 | 0,4564 | 0,4387 |
| 6 | 0,7808 | 0,6161 | 0,5321 | 0,4803 | 0,4447 | 0,4184 | 0,3980 | 0,3817 |
| 7 | 0,7271 | 0,5612 | 0,4800 | 0,4307 | 0,3974 | 0,3725 | 0,3535 | 0,3384 |
| 8 | 0,6798 | 0,5157 | 0,4377 | 0,3910 | 0,3595 | 0,3362 | 0,3185 | 0,3043 |
| 9 | 0,6385 | 0,4775 | 0,4027 | 0,3584 | 0,3286 | 0,3067 | 0,2901 | 0,2768 |
| 10 | 0,6020 | 0,4450 | 0,3733 | 0,3311 | 0,3029 | 0,2823 | 0,2666 | 0,2541 |
Таблица 4
Значения F-критерия для уровня значимости 0,05
( 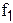 - число степеней свободы большей дисперсии,
- число степеней свободы большей дисперсии, 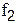 - число степеней свободы меньшей дисперсии)
- число степеней свободы меньшей дисперсии)
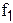
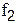
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 161 | 200 | 216 | 225 | 230 | 234 | 237 | 239 | 241 | 242 |
| 2 | 18,51 | 19,00 | 19,16 | 19,25 | 19,30 | 19,33 | 19,36 | 19,37 | 19,38 | 19,39 |
| 3 | 10,13 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,88 | 8,84 | 8,81 | 8,78 |
| 4 | 7,71 | 6,34 | 6,59 | 6,39 | 6,26 | 6,16 | 6,09 | 6,04 | 6,00 | 5,96 |
| 5 | 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,96 | 4,88 | 4,82 | 4,78 | 4,74 |
| 6 | 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,21 | 4,15 | 4,10 | 4,06 |
| 8 | 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | 3,50 | 3,44 | 3,39 | 3,34 |
| 10 | 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | 3,22 | 3,14 | 3,07 | 3,02 | 2,97 |
| 12 | 4,75 | 3,86 | 3,49 | 3,26 | 3,11 | 3,00 | 2,92 | 2,85 | 2,80 | 2,76 |
| 14 | 4,60 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 | 2,77 | 2,70 | 2,65 | 2,60 |
| 3,84 | 2,99 | 2,60 | 2,37 | 2,21 | 2,09 | 2,01 | 1,94 | 1,88 | 1,83 |
Таблица 5
Значение t-критерия для различных уровней значимости
| Число | Уровни значимости | ||||
| степеней свободы | 0,10 | 0,05 | 0,02 | 0,01 | 0,001 |
| 1 | 6,31 | 12,71 | 31,82 | 63,66 | 63,62 |
| 2 | 2,92 | 4,30 | 6,97 | 9,93 | 31,60 |
| 3 | 2,35 | 3,18 | 4,54 | 5,84 | 12,94 |
| 4 | 2,13 | 2,78 | 3,75 | 4,60 | 8,61 |
| 5 | 2,02 | 2,57 | 3,37 | 4,08 | 6,85 |
| 6 | 1,94 | 2,45 | 3,14 | 3,71 | 5,96 |
| 7 | 1,90 | 2,37 | 3,00 | 3,50 | 5,41 |
| 8 | 1,86 | 2,31 | 2,90 | 3,36 | 5,04 |
| 9 | 1,83 | 2,26 | 2,82 | 3,25 | 4,78 |
| 10 | 1,81 | 2,23 | 2,76 | 3,17 | 4,59 |
| 11 | 1,80 | 2,20 | 2,72 | 3,11 | 4,44 |
| 12 | 1,78 | 2,18 | 2,68 | 3,06 | 4,32 |
| 13 | 1,77 | 2,16 | 2,65 | 3,01 | 4,22 |
| 14 | 1,76 | 2,15 | 2,62 | 2,98 | 4,14 |
| 15 | 1,75 | 2,13 | 2,60 | 2,95 | 4,07 |
| 16 | 1,75 | 2,12 | 2,58 | 2,92 | 4,02 |
| 17 | 1,74 | 2,11 | 2,57 | 2,90 | 3,97 |
Таблица 6
Критерии подобия механических и тепловых явлений
| 1. Критерий гомохронности, характеризующий однородность процессов во времени: t - время; v -скорость; l - расстояние | 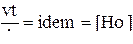
|
| 2. Критерий Ньютона: F - сила; M - масса | 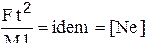
|
| 3. Критерий Фруда: g - ускорение свободного падения | 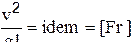
|
| 4. Критерий Эйлера - плотность | 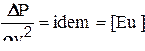
|
5. Критерий Рейнольдса, характеризующий процессы в несжимаемой жидкости:
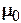 - вязкость - вязкость
| 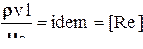
|
6. Критерий Архимеда, характеризующий процесс движения жидкости при различной её плотности:
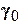 - коэффициент кинематической вязкости - коэффициент кинематической вязкости
| 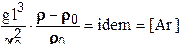
|
| 7. Критерий Жуковского | 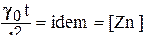
|
8. Критерий Фурье: 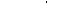 - коэффициент температуропроводности; - коэффициент температуропроводности;  - коэффициент теплоёмкости; - удельный вес - коэффициент теплоёмкости; - удельный вес
| 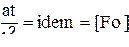
|
| 9. Критерий Пекле для движущейся жидкости с заданным тепловым состоянием | 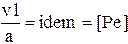
|
| 10. Критерий Нуссельта: - коэффициент теплоотдачи | 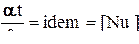
|
| 11. Критерий Кирпичёва: k - коэффициент теплопередачи | 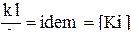
|
| 12. Критерий Прандтля | 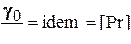
|
13. Критерий Био:
 - постоянная Стефана Больцмана;
- температура - постоянная Стефана Больцмана;
- температура
| 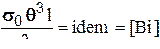
|
Дата: 2019-05-29, просмотров: 427.