Случайной величиной называется переменная величина, которая в результате испытаний может принимать то или значение в границах определённого интервала. Например, действительный размер заготовки под обработку давлением является случайной величиной, так как в процессе её изготовления действует множество случайных факторов.

       Дискретными случайными величинами называются такие, которые принимают отдельные, большей частью целочисленные значения. Например, количество заготовок есть дискретная случайная величина.

       Непрерывной случайной величиной называется такая, которая может принимать любые численные значения из непрерывного ряда возможных значений. Таким образом, действительные размеры заготовки являются непрерывными случайными величинами. Они могут быть заданы в виде функции.

       Для количественной оценки случайных величин пользуются числовыми характеристиками. К числовым характеристикам, определяющим положение центра группировки, относятся: среднее арифметическое, медиана и мода; к характеристикам, определяющим меру рассеяния - дисперсия и среднее квадратичное отклонение.

       Введём числовые характеристики случайной величины для рядов с малым числом наблюдений.

       Пусть, например, при измерении значения предела текучести алюминиевых прутков, изготовленных в одинаковых условиях (на одном оборудовании и по одной технологии), были получены следующие результаты: 177, 174, 178, 176, 175, 175, 173, 171, 167, 177 [MПa], что в сумме составляет 1743. Требуется дать количественные характеристики приведенной случайной величины.

       Формулы для расчёта числовых характеристик случайных величин приведены в табл. 2.1.

       Основными статистическими характеристиками, отражающими среднее положение наблюдаемых значений в ряду, являются средняя арифметическая, медиана и мода.

       Для расчёта медианы (Ме) все измерения располагаются в возрастающий (или убывающий) ряд, после чего в качестве медианы выбирается значение величины, занимающей срединное положение в ряду. При чётном числе измерений медианой будет средняя арифметическая двух значений, расположенных в центре ряда.

       Модой (Мо) называется такое значение случайной величины, которое наблюдается наиболее часто.

       За меру рассеяния принимают сумму квадратов отклонений отдельных значений случайных величин от математического ожидания (среднего арифметического 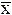 при (n )), делённую на количество наблюдений. Эта мера называется дисперсией.

       Если дисперсия вычисляется при большом числе наблюдений (n ), то она называется генеральной.

Таблица 2.1

Основные статистические характеристики

№	Название характеристики	Расчётная формула
1	Средняя арифметическая из n измерений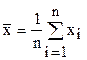
2	Дисперсия генеральная	D(x) =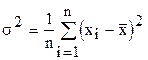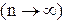
3	Дисперсия выборочная (f=n-1 - число степеней свободы; n - число наблюдений)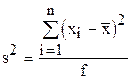
4	Среднее квадратичное отклонение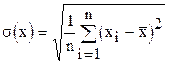
5	Исправленное среднее квадратичное отклонение
6	Коэффициент вариации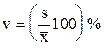
7	Размах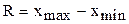

При конечном числе наблюдений дисперсия характеризует разброс значений случайных величин относительно их среднего арифметического. Такая дисперсия s² называется выборочной.

       Вместо дисперсии часто применяют среднее квадратичное отклонение 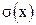. Оно, в отличие от дисперсии, имеет ту же размерность, что и средняя арифметическая.

       Процентное отношение исправленного среднего квадратичного отклонения к средней арифметической называется коэффициентом вариации v. Коэффициент вариации показывает колебание отдельных значений случайной величины около средней арифметической.

       Следует ожидать, что дисперсия больших величин будет больше дисперсии малых величин. Коэффициент вариации исключает это влияние. Будучи безразмерным, он удобен для сравнений.

       Простейшей мерой рассеяния является размах .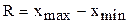

Пример. Пусть из генеральной совокупности в результате n независимых наблюдений над количественным признаком Х извлечена выборка объёма n:

значения признака:	,	,	...,	,
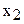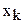частота:	,	,	...,	;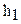

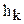причём 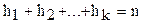. Требуется по данным выборки приближённо оценить неизвестную дисперсию генеральной совокупности.

Р е ш е н и е. Исправленную дисперсию и исправленное среднее квадратичное отклонение вычисляем по формулам:

; .

       В качестве упражнения предлагаем вычислить все введенные характеристики для приведенного выше ряда измеренных значений предела текучести алюминиевых прутков.