Установление закономерностей, которым подчинены случайные явления, основано на изучении статистических данных - результатах наблюдений.
Задачи математической статистики следующие:
1) указать способы сбора и группировки статистических сведений;
2) разработать методы анализа статистических данных, в зависимости от целей исследования.
Пусть требуется изучить совокупность однородных объектов относительно некоторого количественного признака, например, относительно размера детали. Предполагаем, что деталей много и сплошное обследование стоит слишком дорого. Необходимо решить: как путём обследования ограниченного количества деталей сделать вывод о размерном параметре всей совокупности.
Выборочной совокупностью (выборкой) называют совокупность случайно отобранных объектов. Генеральной совокупностью называют совокупность объектов, из которых производится выборка.
Выборка должна быть репрезентативной, т.е. хорошо представлять генеральную совокупность. В силу закона больших чисел можно утверждать, что выборка будет репрезентативной, если её осуществить случайно, т.е. каждый объект из генеральной совокупности достаточно большого объёма (количество объектов в указанной совокупности) отбирается случайно.
Генеральной средней 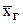 называют среднее арифметическое значений рассматриваемого признака Х генеральной совокупности. Если рассматривать обследуемый признак Х генеральной совокупности как случайную величину, то генеральная средняя будет равна математическому ожиданию признака, т.е.
называют среднее арифметическое значений рассматриваемого признака Х генеральной совокупности. Если рассматривать обследуемый признак Х генеральной совокупности как случайную величину, то генеральная средняя будет равна математическому ожиданию признака, т.е. 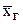 =М(Х).
=М(Х).
Выборочной средней  называют среднее арифметическое признака выборочной совокупности. Выборочная средняя есть средняя взвешенная значений признака
называют среднее арифметическое признака выборочной совокупности. Выборочная средняя есть средняя взвешенная значений признака  с весами, равными соответствующим частотам
с весами, равными соответствующим частотам 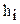 , т.е.
, т.е.
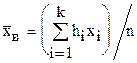 .
.
Дисперсия равна среднему квадратов значений признака минус квадрат общей средней, а именно:
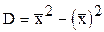 .
.
Эта формула записана на основании теоремы, в которой доказывается, что 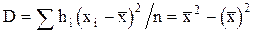 , где
, где 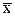 - общая средняя.
- общая средняя.
Пример. Найти дисперсию по распределению:
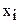
| 1 | 2 | 3 | 4 |
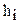
| 20 | 15 | 10 | 5 |
Р е ш е н и е.
 ;
; 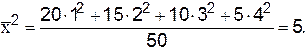
искомая дисперсия 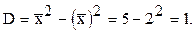
Рассмотрение эмпирического ряда как выборки из генеральной совокупности является основой статистических выводов. В этом смысле эмпирические ряды (см., например, табл. 2.2 для 160-ти измерений предела текучести алюминиевых прутков) являются выборками.
Доверительный интервал. Часто возникает проблема, как на основе ограниченного числа наблюдений (измерений) сделать вывод о величине числовых характеристик генеральной совокупности (математическое ожидание, среднеквадратическое отклонение и т.д.). Так как выборочные наблюдения носят случайный характер, то вычисленные по ним статистические характеристики также колеблются от выборки к выборке. Поэтому для каждой статистической характеристики, вычисленной по данным выборки, следует определить точность оценки. Эта точность содержится в доверительном интервале.
Пусть имеется нормально распределённая генеральная совокупность с математическим ожиданием М и средним квадратичным отклонением s. По результатам отобранной из этой совокупности выборки объёмом n вычислена средняя арифметическая  . Относительно разности М-
. Относительно разности М- 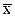 можно с вероятность, например, 95% утверждать, что она находится в интервале
можно с вероятность, например, 95% утверждать, что она находится в интервале 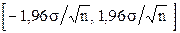 или
или 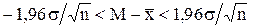
Если вместо доверительной вероятности S=95% желательна, например, вероятность S=99%, то коэффициент 1,96 следует заменить на 2,58.
Дисперсия определяется как средний квадрат отклонения отдельных значений от математического ожидания. Для выборки объёма n имеем:
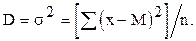
Так как обычно математическое ожидание неизвестно, то вместо приведенной формулы используют соотношение:
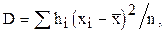
где  - частота значений
- частота значений 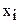 .
.
Часто необходимо знать закон распределения генеральной совокупности. Если закон распределения неизвестен, но имеются основания предположить, что он имеет определённый вид, например R, выдвигают гипотезу о законе распределения R. Задача состоит в том, как подтвердить или опровергнуть выдвинутую статистическую гипотезу.
Возможны статистические гипотезы: о равенстве параметров двух или нескольких распределений, о независимости выборок. Для проверки статистических гипотез используют различные критерии. Заметим, что все критерии не доказываю справедливость той или иной статистической гипотезы, а лишь устанавливают, на принятом уровне значимости, её согласие или несогласие с данными наблюдений.
Для оценки степени близости эмпирического распределения теоретическому существуют специально подобранные случайные величины - критерии согласия Пирсона, Колмогорова, Смирнова и др. Проверка гипотезы о нормальном распределении генеральной совокупности чаще всего осуществляется при помощи критерия согласия Пирсона ( 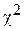 -критерий).
-критерий).
Определение сходимости эмпирического и теоретического распределений с помощью критерия согласия 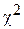 производится следующим образом. Разбиваем всю область изменения случайной величины на m интервалов и подсчитываем количество событий
производится следующим образом. Разбиваем всю область изменения случайной величины на m интервалов и подсчитываем количество событий 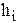 . Затем сравниваем эмпирические
. Затем сравниваем эмпирические 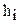 и теоретические
и теоретические 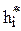 частоты, которые обычно несколько различаются.
частоты, которые обычно несколько различаются.
Случайно ли расхождение частот? Возможно, что расхождение случайно (незначимо) и объясняется малым числом наблюдений, либо способом их группировки и другими причинами. Возможно, что расхождение частот не случайно (значимо) и объясняется тем, что теоретические частоты вычислены, исходя из неверной гипотезы о нормальном распределении генеральной совокупности. Критерий Пирсона отвечает на поставленный выше вопрос.
Итак, для некоторого эмпирического распределения принимаем нулевую гипотезу: генеральная совокупность распределена нормально. Для проверки гипотезы вычисляем критерий Пирсона:
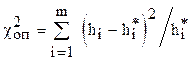 ,
,
где 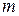 - число сравниваемых частот;
- число сравниваемых частот; 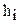 ,
,  - эмпирические и теоретические частоты i-го интервала случайной величины.
- эмпирические и теоретические частоты i-го интервала случайной величины.
Очевидно, что чем меньше различаются теоретические и эмпирические частоты, тем меньше величина критерия и, следовательно, он характеризует близость сравниваемых распределений.
Алгоритм вычисления теоретических частот нормального распределения. следующий:
1. Интервал наблюдаемых значений Х (выборки объёма 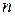 ) делим на
) делим на 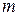 интервалов одинаковой длины. Находим середины каждого интервала и частоту попадания признака в i-ый интервал.
интервалов одинаковой длины. Находим середины каждого интервала и частоту попадания признака в i-ый интервал.
2. Вычисляем выборочные 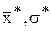 .
.
3. Нормируем случайную величину Х, переходя к 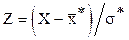
и вычисляем концы интервалов 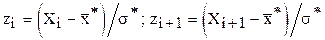 .
.
Здесь наименьшее значение Z= 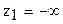 , а наибольшее
, а наибольшее 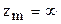 .
.
4. C использованием функции Лапласа Ф(z) (табл.1, Приложение) вычисляем теоретические вероятности 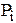 =
= 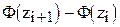 попадания Х в интервалы
попадания Х в интервалы 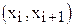 .
.
5. Находим искомые теоретические частоты 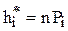 .
.
6. Вычисляем количество степеней свободы по формуле:
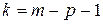 ,
,
где  - число параметров теоретического распределения.
- число параметров теоретического распределения.
7. Задаёмся малой вероятностью - уровнем значимости a. Затем ищем критическую точку исходя из требования, чтобы, при условии справедливости нулевой гипотезы (генеральная совокупность распределена нормально), вероятность того, что рассчитанный критерий 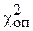 примет значение, больше
примет значение, больше 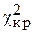 , была равна принятому достаточно малому уровню значимости:
, была равна принятому достаточно малому уровню значимости:
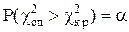 .
.
8. Определяем значение 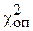 и
и 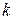 .
.
9. По табл.1 Приложения определяем критическое значение 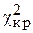 .
.
10. Если 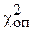 <
< 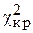 , то делаем вывод: между рассматриваемыми эмпирическим и теоретическим распределением нет существенной разницы.
, то делаем вывод: между рассматриваемыми эмпирическим и теоретическим распределением нет существенной разницы.
Необходимым условием применения критерия 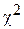 является наличие в каждом из интервалов по меньшей мере 5-10 наблюдений.
является наличие в каждом из интервалов по меньшей мере 5-10 наблюдений.
Пример. При уровне значимости 0,05 проверить гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты:
| эмпирические частоты | 6 | 13 | 38 | 74 | 106 | 85 | 30 | 14 |
| теоретические частоты | 3 | 14 | 42 | 82 | 99 | 76 | 37 | 13 |
Р е ш е н и е. Вычисляем величину критерия 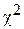 . После вычислений имеем значение
. После вычислений имеем значение 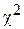 =7,19. Затем находим число степеней свободы k для восьми (m=8) групп выборки k=8-3=5. По таблице 2 Приложения (критические точки распределения
=7,19. Затем находим число степеней свободы k для восьми (m=8) групп выборки k=8-3=5. По таблице 2 Приложения (критические точки распределения 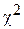 ) при уровне значимости a=0,05 и числе степеней k=5, находим
) при уровне значимости a=0,05 и числе степеней k=5, находим 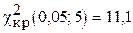 .
.
Так как наблюдаемое значение  , то нет оснований отвергнуть нулевую гипотезу. Иначе, расхождение эмпирических и теоретических частот незначимое и, следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.
, то нет оснований отвергнуть нулевую гипотезу. Иначе, расхождение эмпирических и теоретических частот незначимое и, следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.
Пример. Покажем вычисление 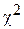 -критерия для проверки нормальности распределения 160-ти значений предела текучести (см. табл.2.2).
-критерия для проверки нормальности распределения 160-ти значений предела текучести (см. табл.2.2).
Распределение, полученное по результатам наблюдений, разбито на 12 интервалов. Первые три и два последних интервала объединены для того, чтобы теоретические частоты получились больше 5. Таким образом, число интервалов стало равным 9. По табл.2 Приложения, в которой содержаться критические значения 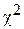 -распределения для различных доверительных вероятностей, вычислили для числа степеней свободы 9-3=6 и S=95% значение
-распределения для различных доверительных вероятностей, вычислили для числа степеней свободы 9-3=6 и S=95% значение 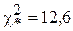 .
.
Число степеней свободы при использовании этого метода равно  , где
, где 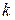 - число интервалов; потеря трёх степеней свободы происходит из-за того, что накладываются следующие три условия: сумма эмпирических частот должна быть равна сумме теоретических, средняя арифметическая должна быть равна математическому ожиданию, выборочное среднее квадратичное отклонение должно быть равно теоретическому.
- число интервалов; потеря трёх степеней свободы происходит из-за того, что накладываются следующие три условия: сумма эмпирических частот должна быть равна сумме теоретических, средняя арифметическая должна быть равна математическому ожиданию, выборочное среднее квадратичное отклонение должно быть равно теоретическому.
Эмпирическое значение 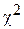 - критерия, вычисленное в примере по формуле, составляет 7,52. Так как эмпирическое значение
- критерия, вычисленное в примере по формуле, составляет 7,52. Так как эмпирическое значение 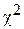 оказалось меньше критического, то можно сделать вывод: распределение предела текучести алюминиевых прутков является нормальным.
оказалось меньше критического, то можно сделать вывод: распределение предела текучести алюминиевых прутков является нормальным.
Пусть выборочное среднее известной генеральной совокупности распределено по нормальному закону с дисперсией 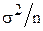 . Если же
. Если же 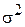 неизвестна, то некоторая величина, характеризующая выборочное среднее, распределена по закону
неизвестна, то некоторая величина, характеризующая выборочное среднее, распределена по закону 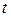 - распределения. Оно сходится к нормальному при n (практически для n100).
- распределения. Оно сходится к нормальному при n (практически для n100).
t-критерий Стьюдента используют для ответа на вопрос какова вероятность того, , что выборка взята из генеральной совокупности с математическим ожиданием М и средним квадратичным отклонением s (или с заданными средней арифметической  и средним квадратичным отклонением).
и средним квадратичным отклонением).
Пусть имеется выборка объёмом n со средней арифметической  и средним квадратичным отклонением . Спрашивается, можно ли эту выборку считать случайным образом отобранной из генеральной совокупности с математическим ожиданием М. Чтобы ответить на поставленный вопрос вычисляют критерий Стьюдента:
и средним квадратичным отклонением . Спрашивается, можно ли эту выборку считать случайным образом отобранной из генеральной совокупности с математическим ожиданием М. Чтобы ответить на поставленный вопрос вычисляют критерий Стьюдента:
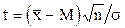 или
или 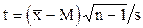 .
.
Для этого из таблицы 5 Приложения берут табличное значение t, для заданного числа степеней свободы и доверительной вероятности. После сравнения вычисленного и табличного значений критерия Стьюдента делается вывод относительно характера отклонения статистических характеристик выборки от генеральной совокупности.
Пример. Исследуется процесс горячего выдавливания прутков на гидравлическом прессе №7 (из восьми установленных в цехе). Требуется проверить нулевую гипотезу о том, что работа пресса №7 в статистическом смысле не отличается от работы всей группы прессов.
Р е ш е н и е. В 10 выборках, продолжительностью одни сутки, наблюдалось следующее количество бракованных прутков на указанной машине: 15, 18, 8, 12, 9, 1, 7, 7, 6, 6.
Среднее количество бракованных прутков, вычисленное по 8-ми машинам, равно 13,54; 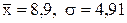 :
:
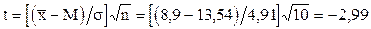 .
.
По таблице 5 Приложения находим значение  для числа степеней свободы, равного 9, и уровня значимости 0,05.
для числа степеней свободы, равного 9, и уровня значимости 0,05.
Вычисленное значение t больше найденного по таблице. Отсюда можно предположить, что отклонение больше случайного (незначимого), т.е определяется некоторыми причинами, которые необходимо установить.
В ы в о д: Среднее значение обрывов проволоки рассматриваемой машины значимо отличается от среднего числа обрывов проволоки на всех восьми гидравлических прессах.
F-критерий Фишера используют в дисперсионном анализе для определения относятся ли взятые выборки к одной и той же генеральной совокупности. Применение критерия предполагает, что выборки взяты из нормально распределённой генеральной совокупности.
Берутся две выборки из одной и той же совокупности. Обычно оценки дисперсии, вычисленных по обеим выборкам, отличаются друг от друга. Тогда F-критерий представляет собой отношение дисперсий:
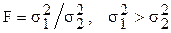 (или
(или 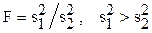 ).
).
Вычисленное значение F-критерия (критерий Фишера) сравниваются с табличным значением.
Пример (однофакторный дисперсионный анализ). Требуется оценить результаты испытаний, которые разделены на несколько групп. Пусть некоторое изделие изготавливается на m однотипных станках и результаты наблюдений, например, размеры деталей можно сгруппировать по отдельным станкам. Необходимо дать ответ на вопрос: Является ли работа станков идентичной ?
Р е ш е н и е. Для определения среднего размера детали для каждого из m станков производятся измерения n идентичных деталей (n параллельных измерений) и по формуле 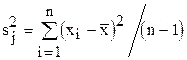 вычисляются дисперсии воспроизводимости. Суммируя полученные значения дисперсий для ряда значений в выбранном интервале изменения фактора, определяется величина
вычисляются дисперсии воспроизводимости. Суммируя полученные значения дисперсий для ряда значений в выбранном интервале изменения фактора, определяется величина 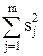 .
.
В процессе измерений обычно имеют место резко выделяющиеся ("дикие" измерения или выбросы), вызывающие соответствующее резкое увеличение значения дисперсии воспроизводимости. Для ответа на вопрос - можно ли отбросить такие измерения, осуществляется проверка однородности дисперсий с использованием критерия Кохрена:
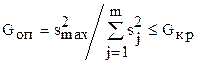 ,
,
где 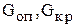 - наблюдаемое (опытное) и критическое значение критерия Кохрена;
- наблюдаемое (опытное) и критическое значение критерия Кохрена; 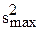 - дисперсия j-ого "дикого" измерения. Значения
- дисперсия j-ого "дикого" измерения. Значения 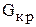 приведены в табл.3 Приложения. Если приведенное условие нарушается, то дисперсии не однородны и "дикие" измерения отбрасываются. После этого все вычисления повторяют без них.
приведены в табл.3 Приложения. Если приведенное условие нарушается, то дисперсии не однородны и "дикие" измерения отбрасываются. После этого все вычисления повторяют без них.
После проверки однородности измерений вычисляется средняя дисперсия воспроизводимости 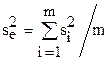 .
.
Пример. Пусть на восьми станках изготавливаются однотипные детали. Требуется, проведя однофакторный дисперсионный анализ, установить - одинакова ли точность работы станков.
Дисперсионный анализ осуществляется в следующем порядке:
1. Для каждого из станков проводим по три параллельных измерения размеров детали и результаты заносим в табл. 2.5.
2. Определяем среднее арифметическое для каждого из станков по результатам параллельных измерений.
3. Вычисляем квадрат разностей между средними арифметическими и результатами параллельных измерений. Вычисляем дисперсии воспроизводимости параллельных измерений при числе степеней свободы f = 3 - 1 = 2. Результаты заносим в табл.
4. Вычисляем сумму дисперсии воспроизводимости для всех станков:
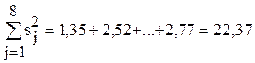 .
.
5. Из табл. видно, что для шестого станка его дисперсия значительно больше остальных. Проверяем однородность дисперсий:
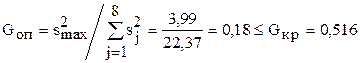 .
.
Видно, что дисперсии однородные и шестое измерение отбрасывать нельзя.
Таблица 2.5
Результаты однофакторного дисперсионного анализа
| j | 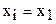
| 
| 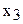
| 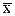
| 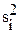
|
| 1 | 68,15 | 66,5 | 65,9 | 66,85 | 1,35 |
| 2 | 68,90 | 66,9 | 66,5 | 67,10 | 2,52 |
| 3 | 61,15 | 61,4 | 58,3 | 60,35 | 2,93 |
| 4 | 62,12 | 61,5 | 58,6 | 60,74 | 3,03 |
| 5 | 72,00 | 68,85 | 70,35 | 70,40 | 2,48 |
| 6 | 71,10 | 68,40 | 72,3 | 70,60 | 3,99 |
| 7 | 64,90 | 65,00 | 61,8 | 63,90 | 3,31 |
| 8 | 61,40 | 58,80 | 61,9 | 60,70 | 2,77 |
Сравнение полученных дисперсий даёт наглядное представление о точности и идентичности работы станков.
Основная идея дисперсионного анализа состоит в сравнении "факторной дисперсии", порождаемой воздействием некоторого качественного фактора, и "остаточной дисперсии", обусловленной случайными причинами. Если различие между этими дисперсиями значимо, то фактор оказывает существенное влияние на изучаемую величину Х.
Для решения вопроса применяют метод разложения дисперсии. Он основан на том, что при различии в работе станков частные средние 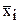 (i=1,2,...,n; в примере i - номер станка, n - количество станков), вычисленные по группам (деталей), отличаются более чем это можно было бы ожидать на основе случайных колебаний отдельных значений.
(i=1,2,...,n; в примере i - номер станка, n - количество станков), вычисленные по группам (деталей), отличаются более чем это можно было бы ожидать на основе случайных колебаний отдельных значений.
Дисперсионный анализ базируется на соотношении
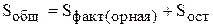 ,
,
где  - общая сумма квадратов отклонений наблюдаемых значений от общей средней
- общая сумма квадратов отклонений наблюдаемых значений от общей средней  ;
; 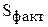 - факторная сумма квадратов отклонений групповых средних от общей средней;
- факторная сумма квадратов отклонений групповых средних от общей средней; 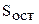 - остаточная сумма квадратов отклонений наблюдаемых значений группы от своей групповой средней (характеризует рассеяние внутри группы).
- остаточная сумма квадратов отклонений наблюдаемых значений группы от своей групповой средней (характеризует рассеяние внутри группы).
По определению
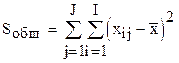 и
и 
где J - число уровней факторов; I - число наблюдений на каждом уровне. Тогда 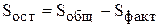 .
.
Разделив суммы квадратов отклонений на соответствующее число степеней свободы получим общую, факторные и остаточные дисперсии:
 ;
; 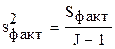 ;
;  .
.
Требуется проверить нулевую гипотезу о равенстве нескольких (J>2) средних нормальных совокупностей с неизвестными, но одинаковыми дисперсиями. Решение этой задачи сводится к сравнению факторной и остаточной дисперсии по критерию Фишера. В этом и состоит суть дисперсионного анализа.
Пример. В волочильном цехе исследовалось восемь волочильных машин относительно числа обрывов проволоки. За десять обследований, продолжительностью каждого сутки, было обнаружено следующее число обрывов проволоки:
Таблица 2.6.
Результаты определения числа обрывов проволоки при волочении
| J | S | Средняя | ||||||||
| I | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| 1 | 13 | 7 | 22 | 15 | 20 | 23 | 15 | 14 | 129 | 16,1 |
| 2 | 18 | 10 | 7 | 12 | 19 | 17 | 18 | 22 | 123 | 15,4 |
| 3 | 8 | 8 | 21 | 14 | 15 | 16 | 8 | 8 | 98 | 12,2 |
| 4 | 13 | 12 | 8 | 10 | 23 | 3 | 12 | 20 | 101 | 12,6 |
| 5 | 12 | 6 | 9 | 27 | 32 | 4 | 9 | 18 | 117 | 14,6 |
| 6 | 6 | 6 | 6 | 17 | 34 | 12 | 1 | 24 | 106 | 13,2 |
| 7 | 16 | 20 | 5 | 9 | 8 | 17 | 7 | 21 | 103 | 12,9 |
| 8 | 21 | 9 | 2 | 13 | 10 | 14 | 7 | 17 | 93 | 11,6 |
| 9 | 17 | 14 | 9 | 24 | 21 | 8 | 6 | 33 | 132 | 16,5 |
| 10 | 16 | 7 | 7 | 10 | 14 | 10 | 6 | 11 | 81 | 10,1 |
| Сред. | 14,9 | 9,9 | 9,6 | 15,1 | 19,6 | 12,4 | 8,9 | 18,8 | 13,54 | |
Число наблюдений с каждой машины i=1...10; число машин j=1...8; IJ=80.
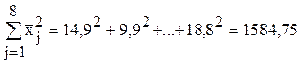 ;
;
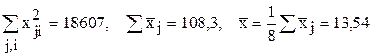 ;
;
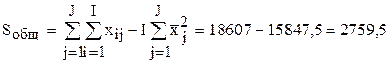 ;
;
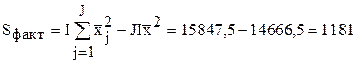 .
.
Таблица 2.7.
Схема разложения дисперсии
| Сумма квадратов отклонений | Число степеней свободы | Дисперсия | |
| Между группами | 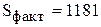
| 8-1=7 | 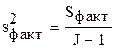 =
168,7 =
168,7
|
| Внутри групп | 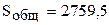
| 89=72 | 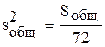 =33,8 =33,8
|
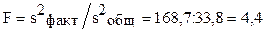 .
.
Для уровня значимости 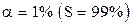 табличное значение критерия Фишера F=2,9. Так как вычисленное значение F значительно больше табличного, можно принять гипотезу: волочильные машины работают неравномерно относительно обрывов проволоки.
табличное значение критерия Фишера F=2,9. Так как вычисленное значение F значительно больше табличного, можно принять гипотезу: волочильные машины работают неравномерно относительно обрывов проволоки.
Пример (двухфакторный анализ). При изготовлении деталей имеется несколько однотипных станков и несколько видов сырья. Задача дисперсионного анализа в этом случае заключается в выяснении значимости данных факторов на размеры обрабатываемых деталей.
Р е ш е н и е. Пусть фактор А - влияние станков, фактор В - влияние качества сырья. Обозначим размер обрабатываемой детали через 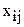 и матрицу двухфакторного эксперимента запишем в табл. 2.8. Пересечение i-го и j-го уровней образует ij-ячейку, в которую записываются наблюдения, полученные при одновременном исследовании факторов А и В на i-ом и j-ом уровнях соответственно.
и матрицу двухфакторного эксперимента запишем в табл. 2.8. Пересечение i-го и j-го уровней образует ij-ячейку, в которую записываются наблюдения, полученные при одновременном исследовании факторов А и В на i-ом и j-ом уровнях соответственно.
Двухфакторный дисперсионный анализ выполняют в следующем порядке.
1. Вычисляем средние значения размеров деталей по каждой из строк и по каждому столбцу.
2. Вычисляем общее среднее по строкам и столбцам.
3. Определяем дисперсию, характеризующую изменение размеров деталей по фактору А (по строкам):  .
.
4. Вычисляем дисперсию, характеризующую изменение размеров деталей по фактору В (по столбцам): 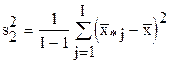 .
.
5. Определяем остаточную дисперсию, характеризующую влияние неучтённых факторов: 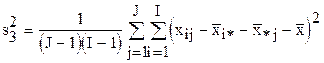 .
.
6. Для выяснения значимости влияния факторов А и В на размер деталей сравниваем дисперсии по факторам с остаточной дисперсией, вычисляя тем самым опытное значение критерия Фишера (F-критерия): 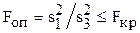 .
.
Выводы: Если наблюдаемое значение F-критерия меньше критического, выбираемого по табл.4 приложения, то влияние факторов А и В на размер деталей незначимо.
Если 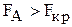 и
и 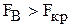 , то влияние факторов А и В значимо.
, то влияние факторов А и В значимо.
На практике часто возникает вопрос - существенно ли влияние отдельного фактора на результат измерений. Например, при изучении зависимости усилия штамповки от степени деформации, требуется определить значимо ли влияние скорости движения инструмента, т.е. можно ли через точки на рис.2.4 провести две зависимости или следует провести одну.
Таблица 2.8.
Матрица двухфакторного дисперсионного анализа
| Партии сырья | Средние | ||||
| Станки | 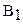
| 
| ... | 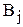
| арифметические |
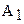
| 
| 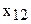
| ... | 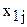
| 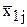
|
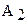
| 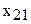
| 
| ... | 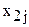
| 
|
| ... | ... | ... | ... | ... | ... |
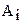
| 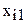
| 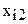
| ... | 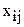
| 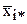
|
| Средние арифметические | 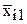
| 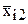
| ... | 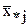
| 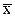
|
Данный анализ проводится в следующем порядке.
1. По формуле: 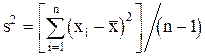 вычисляются дисперсии усилия штамповки при указанных степенях деформации, и по формуле:
вычисляются дисперсии усилия штамповки при указанных степенях деформации, и по формуле: 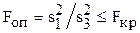 определяется наблюдаемое значение F-критерия. Если наблюдаемое значение F-критерия окажется меньше критического, то сравниваемые дисперсии есть выборки из одной генеральной дисперсии, т.е. точность измерения усилий штамповки при равных скоростях движения инструмента одинакова.
определяется наблюдаемое значение F-критерия. Если наблюдаемое значение F-критерия окажется меньше критического, то сравниваемые дисперсии есть выборки из одной генеральной дисперсии, т.е. точность измерения усилий штамповки при равных скоростях движения инструмента одинакова.
2. Проводится сравнение двух средних арифметических. Для этого используется сравнение по критерию Стьюдента (t - критерию).
Опытное значение t - критерия получим по формуле: 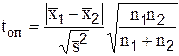 ,
,
где 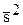 - средняя дисперсия, которая определяется выражением:
- средняя дисперсия, которая определяется выражением: 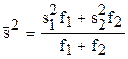
 с числом степеней свободы
с числом степеней свободы 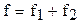 .
.
Фиг.2.4. Зависимость усилий штамповки от степени деформации
(скорости перемещения инструмента: V1=10 мм/c, V2=12мм/c)
Если опытное значение t - критерия окажется больше критического, определяемого по табл. 5 Приложения, то влияние скорости перемещения инструмента на усилие штамповки значимо и через точки на рис.2.4 следует провести две зависимости.
Регрессия и корреляция
До сих пор обсуждаемые методы обработки данных касались в основном одного признака. Важной статистической задачей является установление существования взаимосвязи между несколькими факторами (например, необходимо выяснить, изменяются ли два признака самостоятельно, независимо друг от друга, или изменение одного из них вызвано варьированием другого).
Рассмотрим случай, когда у изделия (или процесса) замеряются два признака 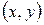 . При этом могут возникать следующие варианты:
. При этом могут возникать следующие варианты:
1. Оба признака 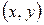 тесно связаны друг с другом (например, длина ребра и объём куба). Этот вид связи называют функциональной. Функциональная связь (или зависимость) между признаками выражается конкретной формулой.
тесно связаны друг с другом (например, длина ребра и объём куба). Этот вид связи называют функциональной. Функциональная связь (или зависимость) между признаками выражается конкретной формулой.
2. Оба признака не строго связаны друг с другом. В этом случае отдельно взятому значению признака  может соответствовать ряд распределения значений
может соответствовать ряд распределения значений 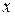 . Если это распределение значений
. Если это распределение значений 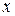 не изменяется с изменением величины
не изменяется с изменением величины  , то оба признака
, то оба признака 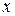 и
и  не зависят друг от друга.
не зависят друг от друга.
3. Если для каждого фиксированного значения  получают распределение признака
получают распределение признака 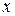 и, наоборот, для каждого фиксированного значения
и, наоборот, для каждого фиксированного значения 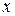 получают распределение признака
получают распределение признака  , то между этими признаками имеется статистическая (корреляционная) связь.
, то между этими признаками имеется статистическая (корреляционная) связь.
При анализе данных, требуется выявить независимые параметры. Для установления корреляционной связи между переменными 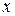 и
и  результаты наблюдений представляют в виде корреляционной матрицы (табл. 2.9). Для этого значения
результаты наблюдений представляют в виде корреляционной матрицы (табл. 2.9). Для этого значения 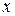 и
и  разбивают на ряд интервалов и определяют средние значения интервалов. В ячейки, образованные пересечением строк и столбцов, заносятся частоты попадания пар значений
разбивают на ряд интервалов и определяют средние значения интервалов. В ячейки, образованные пересечением строк и столбцов, заносятся частоты попадания пар значений 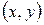 в соответствующие интервалы по
в соответствующие интервалы по 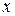 и
и  . В последние строку и столбец записывают суммарные частоты по соответствующим стокам и столбцам.
. В последние строку и столбец записывают суммарные частоты по соответствующим стокам и столбцам.
Уже из обзора табл. 2.9 видно, что с возрастанием 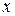 возрастает и
возрастает и  . Однако эту связь нужно выразить количественно и оценить статистически.
. Однако эту связь нужно выразить количественно и оценить статистически.
Эта оценка производится следующим образом.
1. Вычисляем частные средние значения для 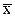 по строкам. Для первой строки значения
по строкам. Для первой строки значения 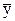 =25 соответствуют значениям
=25 соответствуют значениям 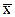 =11 и 13 с частотами 3 и 2. Частная средняя этих значений равна
=11 и 13 с частотами 3 и 2. Частная средняя этих значений равна 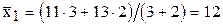 ;
;
для второй строки - 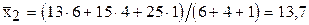 .
.
2. Результаты вычисления частных средних для всех строк запишем в табл.2.10.
3. Отложив данные табл.2.10 на графике, получим корреляционную зависимость  от
от 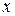 .
.
Связь между двумя количественными признаками проявляется в виде определённой тенденции. Например, если один признак увеличивается, то другой увеличивается или уменьшается. На практике связь между признаками в интересующей экспериментатора области бывает линейной или допускающей линеаризацию (например, логарифмированием, извлечением корня, разложением в ряд и отбрасыванием малых высшего порядка малости).
"Наилучшая" прямая, выравнивающая опытные данные, определяется методом наименьших квадратов, при котором сумма квадратов отклонений  по по вертикали от найденной прямой должна быть минимальной. Эта наилучшая прямая называется линией регрессии у относительно
по по вертикали от найденной прямой должна быть минимальной. Эта наилучшая прямая называется линией регрессии у относительно 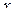 .
.
Таблица 2.9
Корреляционная матрица
| x y | 10-12 11 | 12-14 13 | 14-16 15 | 16-18 17 | 18-20 19 | 20-22 21 | 22-24 23 | 24-26 25 | 26-28 27 | 28-30 29 | 30-32 31 | 32-34 33 | 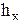
|
| 20-30 25 | 3 | 2 | 5 | ||||||||||
| 30-40 35 | 6 | 4 | 1 | 11 | |||||||||
| 40-50 45 | 1 | 13 | 5 | 19 | |||||||||
| 50-60 55 | 1 | 2 | 4 | 8 | 15 | ||||||||
| 60-70 65 | 1 | 4 | 4 | 2 | 11 | ||||||||
| 70-80 75 | 2 | 6 | 6 | 1 | 15 | ||||||||
| 80-90 85 | 1 | 5 | 6 | ||||||||||
| 90-100 | 1 | 4 | 1 | 6 | |||||||||
| 100-110 | 2 | 4 | 1 | 1 | 8 | ||||||||
| 110-120 | 1 | 1 | 2 | ||||||||||
| 120-130 | 1 | 1 | |||||||||||
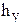
| 3 | 10 | 20 | 9 | 14 | 11 | 9 | 8 | 6 | 6 | 1 | 3 | 100 |
Таблица 2.10
Значения частных средних
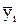
| 25 | 35 | 45 | 55 | 65 | 75 | 85 | 95 | 105 | 115 | 125 |
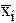
| 12 | 13,7 | 15,4 | 17,5 | 20,1 | 21,8 | 24,7 | 27,0 | 29,3 | 31 | 33 |
Если обозначить через 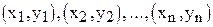 наблюдаемые значения признаков, то линия регрессии выразится в виде
наблюдаемые значения признаков, то линия регрессии выразится в виде 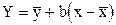 , где
, где 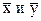 - средние арифметические.
- средние арифметические.
Коэффициент регрессии b определяется по формуле:
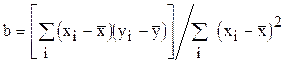 .
.
Если рассматривать характер изменения х по у, т.е. что х зависит от значений признака у, тогда линия регрессии будет иметь вид:
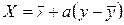 , где
, где 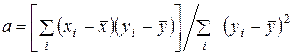 .
.
Заметим, что две линии регрессии, вычисленные по приведенным формулам в случае статистической связи признаков х и у не совпадают.
Тесноту связи между признаками характеризует коэффициент корреляции:
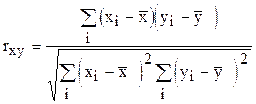 или
или 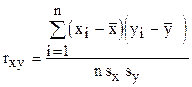 ,
,
где 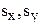 - среднеквадратические отклонения.
- среднеквадратические отклонения.
Чтобы оценить достоверность коэффициента корреляции, необходимо предварительно оценить его ошибку 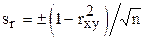 .
.
Далее определяется критерий существенности: 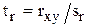 .
.
Если величина 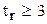 , то коэффициент корреляции считается достоверным, т.е. связь между двумя факторами является доказанной. Если
, то коэффициент корреляции считается достоверным, т.е. связь между двумя факторами является доказанной. Если 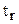 <3, то связь отсутствует.
<3, то связь отсутствует.
Коэффициент корреляции принимает значения в интервале -1, +1. Если 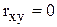 , то линейная связь между признаками х и у отсутствует. Если же, наоборот,
, то линейная связь между признаками х и у отсутствует. Если же, наоборот, 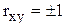 , то между признаками существует линейная функциональная связь. Если r>0, то связь прямая, а если r<0, то связь обратная. В зависимости от величины коэффициента корреляции делают следующие заключения:
, то между признаками существует линейная функциональная связь. Если r>0, то связь прямая, а если r<0, то связь обратная. В зависимости от величины коэффициента корреляции делают следующие заключения:
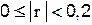
| практически нет связи; |
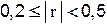
| слабая связь; |
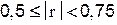
| средняя связь; |
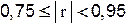
| сильная связь; |
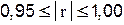
| практически функциональная связь. |
Регрессионный анализ позволяет представить результаты эксперимента в виде функциональной зависимости. В частности, результат эксперимента (функция отклика) может быть описан полиномом:
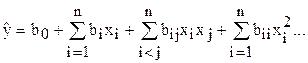 .
.
Введенное уравнение называют уравнением регрессии.
Уравнение регрессии - это приближённая математическая модель процесса или явления, полученная на основе экспериментальных данных. Уравнение адекватно описывает результаты опытов, если среднеквадратичные отклонения экспериментальных данных не превышают ошибку воспроизводимости значений, рассчитанных по уравнению регрессии, т.е. расчётная кривая лежит в поле разброса экспериментальных данных.
Значения коэффициентов регрессии могут быть вычислены методом наименьших квадратов, либо методом ортогональных планов (см. пример в главе 3). После вычисления коэффициентов регрессии осуществляется проверка их значимости. Целью её является выяснение того, с какой степенью достоверности полученные значения коэффициентов регрессии отличаются от нуля.
Для проверки значимости коэффициентов регрессии вычисляется средняя дисперсия воспроизводимости 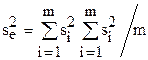 (m - число опытов в одной из серий). Далее вычисляется дисперсия коэффициентов регрессии
(m - число опытов в одной из серий). Далее вычисляется дисперсия коэффициентов регрессии 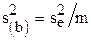 и с использованием t-критерия осуществляется проверка коэффициентов регрессии по формуле
и с использованием t-критерия осуществляется проверка коэффициентов регрессии по формуле 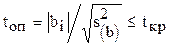 .
.
Если опытное значение t-критерия для какого-либо коэффициента регрессии окажется равным или меньше критического, то данный коэффициент регрессии незначим и влиянием фактора, характеризующегося данным коэффициентом, можно пренебречь.
После оценки значимости коэффициентов регрессии переходим к проверке адекватности (соответствия) выбранного уравнения регрессии опытным данным. Для этого вычисляем дисперсию, характеризующую неадекватность уравнения регрессии:
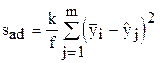
где k - число параллельных измерений; m - число отдельных измерений в одной из серий опытов; f=m-q - число степеней свободы; q - число коэффициентов регрессии; 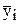 - среднее значение результатов измерений;
- среднее значение результатов измерений; 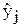 значение результатов измерений, вычисленных по уравнению регрессии (вычисления значений
значение результатов измерений, вычисленных по уравнению регрессии (вычисления значений 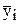 производятся путём подстановки численных значений коэффициентов регрессии в выбранное уравнение регрессии).
производятся путём подстановки численных значений коэффициентов регрессии в выбранное уравнение регрессии).
Определяем опытное значение F-критерия (критерия Фишера):
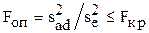 ,
,
где 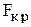 - критическое значение критерия Фишера, определяемое по табл.4 Приложения;
- критическое значение критерия Фишера, определяемое по табл.4 Приложения; 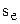 - средняя дисперсия воспроизводимости.
- средняя дисперсия воспроизводимости.
Если опытное значение F-критерия окажется меньше или равно критическому, то принятое уравнение регрессии адекватно описывает экспериментальные данные.
Для применения методов регрессионного анализа необходимо соблюдение следующих условий: значения изучаемых параметров процесса в каждом опыте должны быть независимыми, нормально распределёнными случайными величинами; при этом ошибка в параметрах системы, начальных и граничных условиях должна быть пренебрежимо мала по сравнению с ошибкой в параметрах процесса; дисперсии параметров системы при переходе от опыта к опыту должны быть однородными при достаточной повторяемости опытов.
При обработке эксперимента необходимо наилучшим образом выбрать форму представления его результатов. В качестве такой формы при конструировании математических моделей целесообразно выбирать степенные, экспоненциальные и тригонометрические ряды или их отрезки.
Существенное значение при обработке экспериментальных данных занимает линеаризация эмпирических зависимостей, например, путём логарифмирования экспоненциальных зависимостей. Для некоторой фиксированной и ограниченной области варьирования параметров нелинейные модели (уравнения регрессии) можно привести к линейному виду путём разложения в ряд Тейлора.
Результаты эксперимента могут быть представлены в таблицах, На фотоснимках, на осциллограммах и лентах регистрирующих приборов, в виде записей на магнитные ленты и диски и т.д. Эта информация называется необработанными данными. Обработанные данные составляет та же информация после математической обработки и наглядного (в виде диаграмм, схем, рисунков, графиков и т.д.) представления результатов.
Для дальнейшего изучения предмета рекомендуем использовать руководства по корреляционному и регрессионному анализу, например, монографию Э. Фёрстер, Б. Ренц "Методы корреляционного и регрессионного анализа" M.: Финансы и статистика, 1983. - 302 с.
ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА ДЛЯ ЭКСТРЕМАЛЬНЫХ ЗАДАЧ
При определении оптимальных условий протекания процессов обычно применялся метод поочерёдного варьирования факторов, в частности, метод Гаусса-Зайделя, при котором исследуется окрестность исходной точки, выбирается направление движения к оптимуму и осуществляется малый шаг в этом направлении. Преимуществом метода математического планирования экспериментов является одновременное варьирование всех влияющих факторов и движение к оптимуму кратчайшим путём с минимальным количеством опытов. Начало математическому планированию экспериментов положено в конце 20-х, начале 30-х годах работами Р. Фишера в области дисперсионного анализа и работами Бокса с сотрудниками в 50-х годах. Именно Фишер впервые показал целесообразность одновременного варьирования всеми факторами в противовес широко распространенному однофакторному варьированию. В нашей стране математическое планирование экспериментов получило развитие после выхода в свет в 1965 году книги В.В. Налимова и Н.А. Черновой [9].
Планирование экспериментов имеет большое значение при постановке исследований, направленных на изучение сложных систем и различных многофакторных объектов. Планирование эксперимента повышает его эффективность, даёт наглядную интерпретацию результатов, позволяет уменьшить и оценить случайные и систематические ошибки.
Цели, которые ставятся и решаются при планировании эксперимента во многом совпадают с целями и задачами теории подобия и моделирования. В частности, теория подобия, ставит своей задачей так обобщить опытные данные, чтобы любой эксперимент мог быть закономерно перенесён на неограниченно большой класс явлений, которые признаются подобными данному явлению. Современные тенденции синтеза теории и эксперимента свидетельствуют о целесообразности объединения методов теории подобия и моделирования и планирования эксперимента.
Планирование эксперимента отводит математическим методам активную роль. Здесь статистические методы используются на всех стадиях исследования: при формализации априорной информации перед постановкой опытов; при выборе факторов, влияющих на свойства объекта исследования; при постановке экспериментов и обработке их результатов; при принятии решений.
Как уже отмечалось, основная идея метода планирования - возможность целенаправленного оптимального управления экспериментом при неполном знании механизма изучаемого явления - отвечает идеям кибернетического подхода, предусматривающего формализацию нетворческой части труда исследователя.
При планировании эксперимента существенную роль играют концепции рандомизации и оптимального использования пространства независимых переменных.
Рандомизацией эксперимента называют целенаправленное проведение запланированных опытов в случайной последовательности, с тем чтобы исключить влияние систематических ошибок, вызванных внешними условиями.
В планировании эксперимента используют матрицы планирования, в которых записывают кодированные значения факторов (оба эти понятия будут подробнее рассмотрены).
Если точки в матрице планирования выбраны так, что точность предсказания значений исследуемого параметра одинакова на равных расстояниях от центра факторного пространства и не зависит от направления, то это свойство называется ротатабельностью.
Комбинация факторов, влияющих на проведение эксперимента, называется уровнем факторов. Если число факторов k известно, то можно найти число опытов 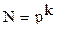 для реализации всех возможных сочетаний уровней факторов (p - число уровней).
для реализации всех возможных сочетаний уровней факторов (p - число уровней).
Если реализуются все возможные сочетания уровней факторов, то эксперимент называется полным факторным. Наряду с ним применяются дробные реплики от полного факторного эксперимента, которыми пользуются для того, чтобы получить линейное приближение небольшого участка поверхности отклика. Целесообразность применения дробных реплик возрастает с ростом числа факторов.
Общая схема планирования экспериментов для решения экстремальных задач состоит из следующих этапов: 1) постановка задачи; 2) выбор параметров оптимизации; 3) выбор факторов; 4) составление линейного плана; 5) реализация линейного плана и построение линейной модели; 6) поиск области экстремума; 7) описание области экстремума; 8) интерпретация результатов.
Выбор параметра оптимизации
Параметр оптимизации – признак, по которому мы хотим оптимизировать процесс. Это может быть зависимая переменная, отклик, выход, целевая функция. Параметр оптимизации должен удовлетворять ряду требований: иметь ясный физический смысл, быть единственным и однозначным в статистическом смысле (является количественным показателем - числом, должен иметь область определения), в экстремальных задачах иметь экстремум. Мы должны уметь его измерять при любой возможной комбинации выбранных уровней факторов.
Статистическая эффективность требует выбора зависимой переменной так, чтобы она определялась с максимальной точностью. Однозначность в статистическом смысле означает, что набору значений независимых переменных должно соответствовать одно с точностью до ошибки эксперимента значение функции отклика.
В технике редко решаются задачи с одной независимой переменной. Параметров оптимизации, как правило, много. Однако, необходимо стремиться к одному параметру оптимизации. Для этого применяют метод априорного ранжирования. Сложную задачу целесообразно свести к последовательности более простых оптимизационных задач. При этом прочие характеристики процесса выступают уже не в качестве параметров оптимизации, а содержат ограничения.
Примерная классификация параметров оптимизации:
- экономические: прибыль, рентабельность, себестоимость, затраты на эксперимент;
- технико-экономические: рентабельность, производительность, надежность, долговечность, КПД;
- технико-технологические: выход продукта, его физические и механические характеристики;
- прочие: психологические, эстетические, статистические (например, уменьшение числа выбросов за пределы допустимого интервала).
Параметр оптимизации должен оценивать действительную эффективность процесса в выбранном смысле – в этом заключается корректность постановки собственно задачи! Параметр оптимизации может изменяться в процессе решения задачи поскольку меняются цели и приоритеты. Он должен давать оценку эффективности системы в целом, а не ее отдельных частей.
Дата: 2019-05-29, просмотров: 442.