Регрессионный анализ позволяет представить результаты эксперимента в виде функциональной зависимости. В частности, результат эксперимента (функция отклика) может быть описан полиномом:

.

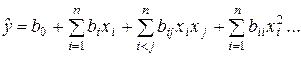Введенное уравнение называют уравнением регрессии.

       Уравнение регрессии - это приближённая математическая модель процесса или явления, полученная на основе экспериментальных данных. Уравнение адекватно описывает результаты опытов, если среднеквадратичные отклонения экспериментальных данных не превышают ошибку воспроизводимости значений, рассчитанных по уравнению регрессии, т.е. расчётная кривая лежит в поле разброса экспериментальных данных.

        Для применения методов регрессионного анализа необходимо соблюдение следующих условий: значения изучаемых параметров процесса в каждом опыте должны быть независимыми, нормально распределёнными случайными величинами; при этом ошибка в параметрах системы, начальных и граничных условиях должна быть пренебрежимо мала по сравнению с ошибкой в параметрах процесса; дисперсии параметров системы при переходе от опыта к опыту должны быть однородными при достаточной повторяемости опытов.

       При обработке эксперимента необходимо наилучшим образом выбрать форму представления его результатов. В качестве такой формы при конструировании математических моделей целесообразно выбирать степенные, экспоненциальные и тригонометрические ряды или их отрезки.

       Существенное значение при обработке экспериментальных данных занимает линеаризация эмпирических зависимостей, например, путём логарифмирования экспоненциальных зависимостей. Для некоторой фиксированной и ограниченной области варьирования параметров нелинейные модели (уравнения регрессии) можно привести к линейному виду путём разложения в ряд Тейлора.

       Результаты эксперимента могут быть представлены в таблицах, На фотоснимках, на осциллограммах и лентах регистрирующих приборов, в виде записей на магнитные ленты и диски и т.д. Эта информация называется необработанными данными. Обработанные данные составляет та же информация после математической обработки и наглядного (в виде диаграмм, схем, рисунков, графиков и т.д.) представления результатов.

       Значения коэффициентов регрессии могут быть вычислены методом наименьших квадратов, либо методом ортогональных планов. После вычисления коэффициентов регрессии осуществляется проверка их значимости. Целью её является выяснение того, с какой степенью достоверности полученные значения коэффициентов регрессии отличаются от нуля.

Для расчета коэффициентов регрессии по методу ортогональных планов используем уже известную нам формулу:

,

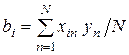где 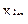 -  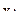в n-ом опыте;  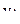- значение параметра оптимизации.

       Попробуем теперь понять, каким образом получена последняя формула. Для этого рассмотрим метод наименьших квадратов. Указанный метод является одним из самых популярных в математике и имеет очень широкую область приложения. Он был разработан Гауссом и Лежандром около 200 лет назад.

       Возьмем простейшее (линейное) уравнение регрессии:

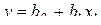.                                                                                                                 (3.41)

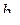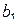       В данном случае это просто уравнение прямой. Необходимо вычислить неизвестные коэффициенты и . Если бы все экспериментальные точки лежали строго на прямой, то для каждой из них было бы справедливо равенство:

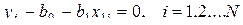
       На практике это условие обычно нарушается и вместо него имеем выражение:

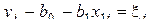,                                                                                                     (3.42)

где  - разность между экспериментальным и вычисленным значением. Эту величину называют невязкой. Будем искать коэффициенты регрессии, при которых невязка будет минимальной. Запишем это требование в следующем виде:

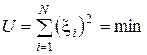.                                                                                                     (3.43)

       Метод наименьших квадратов (МНК) обладает тем свойством, что делает определенной любую произвольную систему уравнений. В нашем уравнении (3.41) было 2 неизвестных коэффициента, значит применяя МНК мы должны получить два уравнения. Перепишем соотношение (3.43) в следующем виде:

.

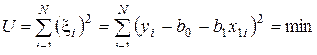       Известно, что минимум функции достигается при равенстве нулю частных производных по всем неизвестным, т.е. в данном случае .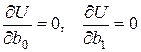

       Тогда получаем:

.

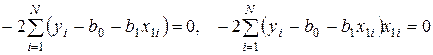       После простых преобразований получаем:

.

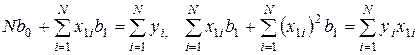       Окончательно формулы для вычисления определителей имеют вид:

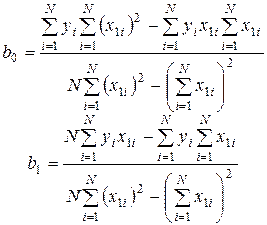.                                                                       (3.44)

       В случае, если мы имеем дело с матрицей планирования, используем свойства симметрии и нормировки: 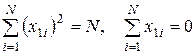. Тогда (3.44) переходят в уже известные нам формулы.

Для расчёта коэффициентов регрессии столбцу  надо приписать знаки соответствующего столбца 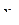, затем необходимо сложить значения параметров оптимизации со своими знаками и результат разделить на число опытов матрицы планирования.

Пример. В случае восьми опытов согласно полуреплике 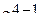 будем иметь матрицу планирования, которая показана в таблице 3.9.

       Расчёт коэффициентов регрессии следующий:

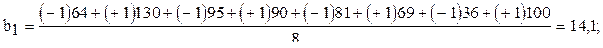
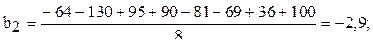
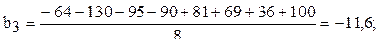
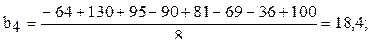
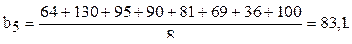
       Аналогично рассчитываются эффекты и при парных взаимодействиях .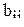

Таблица 3.9

Матрица планирования  и результаты эксперимента

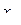
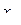
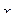
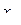
№ опыта						у
1	+	-	-	-	-	64
2	+	+	-	-	+	130
3	+	-	+	-	+	95
4	+	+	+	-	-	90
5	+	-	-	+	+	81
6	+	+	-	+	-	69
7	+	-	+	+	-	36
8	+	+	+	+	+	100

       Ранее мы рассмотрели, как подсчитывается дисперсия в каждом конкретном опыте. На практике       матрица планирования состоит из серий опытов, и дисперсия всего эксперимента получается в результате усреднения всех опытов. По терминологии, принятой в планировании эксперимента, речь идет о подсчете дисперсии параметра оптимизации 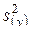 или, что тоже самое, дисперсии воспроизводимости.

В общем случае дисперсия, характеризующая ошибку в определении коэффициентов регрессии:

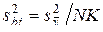, где 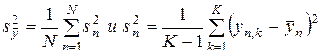,                      (3.51)

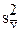 - дисперсия опытов;  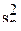- оценка дисперсии;  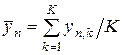- среднее значение результатов; K - число повторных серий опытов.

       Дисперсию воспроизводимости проще всего рассчитывать, когда соблюдается равенство числа повторных опытов во всех экспериментальных точках. На практике часто встречаются случаи, когда число повторных опытов различно, например, в случае отброса результатов грубых наблюдений, еще каких-либо эмпирических соображений. Тогда при расчетах следует пользоваться средневзвешенным значением дисперсий, взятых с учетом числа степеней свободы.

.

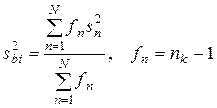       Заметим, что формулами (3.51) можно пользоваться только в том случае если дисперсии однородны. Поэтому далее следует проверить предпосылки регрессионного анализа об однородности выборочных дисперсий 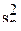, по критерию Кохрена

.

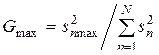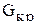Если вычисленное значение  окажется меньше , найденного из соответствующей таблицы для  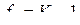и 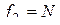, то гипотеза об однородности дисперсии принимается.

После расчёта коэффициентов регрессии следует проверить их статистическую значимость. С этой целью рассчитывают доверительные интервалы коэффициентов регрессии 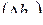, В случае планов первого порядка при использовании как полного факторного эксперимента, так и регулярных дробных реплик доверительные интервалы для всех коэффициентов (в том числе и эффектов взаимодействия) равны друг другу (одинаковы). Прежде всего необходимо найти дисперсию коэффициента регрессии, а далее определяем доверительный интервал для коэффициентов регрессии по формуле: 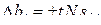, где t – табличное значение критерия Стьюдента при уровне значимости (определяем по таблице); N - число степеней свободы. Коэффициент регрессии статистически значимый, если его абсолютное значение равно или больше величины доверительного интервала. Доверительный интервал задается верхней и нижней границам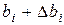и:  и 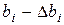. Простейший пример. Допустим в двух задачах оказались два численно равных коэффициента регрессии, но с разными доверительными интервалами. Значимым будет только второй.

Задача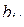
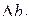
1	5,5	5,6
2	5,5	5,2

       В общем случае чем уже доверительный интервал (при заданном значении 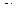), тем с большей уверенностью можно говорить о значимости коэффициента.

В процессе статистического анализа уравнения регрессии проверяют гипотезу об адекватности рассматриваемого уравнения, т.е. отвечают на вопрос, соответствует ли полученное уравнение изучаемому явлению или необходима более сложная модель.

       Дисперсия неадекватности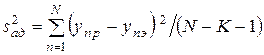   

служит количественным показателем адекватности полученной модели. Здесь 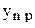 - значение параметра оптимизации в n-ом опыте, предсказанное уравнением регрессии;  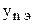- экспериментальное значение параметра в том же опыте. Знаменатель формулы содержит число степеней свободы. Напомним, что такое число степеней свободы. В статистике так называют разность между числом опытов и числом коэффициентов, которые уже вычислены по результатам этих опытов независимо друг от друга. Заметим, что здесь не следует учитывать, например, опыты в нулевой точке для линейной модели.

       Правило: в планировании эксперимента число степеней свободы для дисперсии адекватности равно числу различных опытов, результаты которых используются при подсчете коэффициентов регрессии, минус число определяемых коэффициентов.

       Схема расчёта дисперсии неадекватности для рассматриваемого примера приведена в табл. 3.10.

Дисперсия неадекватности .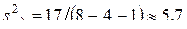

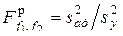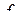       Гипотезу об адекватности проверяют с помощью критерия Фишера (F-критерия): , где  и 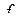 - число степеней свободы при определении дисперсий неадекватности  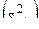и опыта .

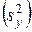Таблица 3.10

К расчёту дисперсии неадекватности

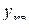
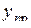
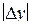
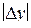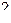
Номер опыта					Номер опыта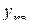
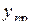
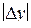
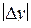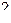
1	64	65	1	1	5	81	79	2	4
2	130	130	0	0	6	69	70	1	1
3	95	96	1	1	7	36	36	0	0
4	90	87	3	9	8	100	101	1	1
									17

       Гипотеза об адекватности линейной модели может быть принята, если расчётное значение F-критерия 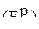 не превышает его табличного значения 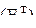, которое приводится в таблицах по математической статистике для выбранного уровня значимости. Для рассмотренного случая имеем 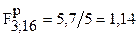. При 5%-ном уровне значимости (=0,05) табличное значение F-критерия . Так как 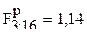< 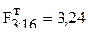, то гипотеза об адекватности линейного уравнения не отвергается, и его можно использовать для следующих этапов эксперимента. В противном случае уравнение необходимо дополнить членами более высокого порядка.

     Адекватная линейная модель, которую мы рассматривали (и получили) имеет вид полинома первой степени. Коэффициенты полинома являются частными производными функции отклика по соответствующим переменным. Их геометрический смысл – тангенсы углов наклона гиперплоскости к соответствующей оси. Больший по абсолютной величине коэффициент соответствует большему углу наклона и , следовательно, более существенному изменению параметра оптимизации при изменении данного фактора.

Интерпретация результатов:

· Устанавливается, в какой мере каждый из факторов влияет на параметр оптимизации; количественная мера влияния – коэффициент регрессии; о характере влияния говорят знаки коэффициентов; интерпретация знаков зависит от того – ищем мы минимум или максимум;

· Далее выясняется, как расположить совокупность факторов в ряд по силе их влияния на параметр оптимизации, здесь играет роль значимость коэффициентов;

· Изменение интервалов варьирования меняет коэффициенты регрессии, инвариантными к изменению интервалов остаются знаки линейных коэффициентов – и они могут поменяться на обратные, если при движении по градиенту мы “проскочим” экстремум.

Принятие решений после построения модели. Возможны варианты:

1. все коэффициенты регрессии значимы;

2. часть коэффициентов регрессии значима, часть незначима;

3. все коэффициенты регрессии незначимы.

В каждом варианте оптимум может быть близко, далеко, или информация вообще может отсутствовать.

В первом случае если область оптимума близка возможно:

· окончание решения;

· переход к планам второго порядка (Налимов, Чернова);

· движение по градиенту – используется при малой ошибке опыта, поскольку на фоне большой ошибки трудно установить значение параметра оптимизации.

Если область оптимума далека или неизвестна, выход – движение по градиенту. опыта и т.д.). Наконец, третий вариант: все коэффициенты незначимы (кроме коэффициента 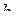). Чаще всего это происходит при узких интервалах либо больших ошибках опыта. Варианты: улучшение методики проведения опытов, постановка параллельных опытов. Если область оптимума близка (если есть информация), возможно также окончание опытов.

Если линейная модель неадекватна, значит не удается аппроксимировать поверхность отклика плоскостью. Формальные признаки этого (кроме величины F - критерия) следующие:

1. значимость хотя бы одного из коэффициентов взаимодействия;

2. значимость суммы коэффициентов регрессии при квадратичных членах 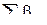. Оценкой этой суммы служит разность между 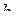и значением зависимой переменной в центре плана 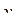. Если разность превосходит ошибку опыта, то гипотеза о незначимости коэффициентов при квадратичных членах не может быть принята.

Решения, принимаемые для получения адекватной модели:

· изменение интервалов варьирования;

· перенос центра плана;

· достройка плана.

Еще одно решение: включение в модель эффектов взаимодействия и движение с помощью неполного полинома второго порядка. Этот прием с получением и анализом уравнений второго порядка. Направление градиента будет меняться от точки к точке.