Ряды с большим числом наблюдений требуют определённого порядка работы. Рассмотрим таблицу 2.2, в которой приведены результаты 160-ти измерений значений предела текучести алюминиевых прутков, изготовленных в одинаковых условиях.
Для обозримости полученных результатов, значения случайной величины сначала располагают в порядке их возрастания и затем подсчитывают частоты отдельных наблюдений. В результате имеем таблицу 2.3, в которой приведен упорядоченный ряд наблюдений.
Упорядоченный ряд даёт наглядную картину полученных результатов. В частности, видно какие наблюдения встречаются чаще других. Имея упорядоченный ряд, можно по результатам измерений построить полигон частот (см. фиг.2.1).
Таблица 2.2.
Результаты 160-ти измерений предела текучести алюминиевых прутков
| 171 | 177 | 175 | 177 | 174 | 174 | 173 | 183 | 183 | 178 |
| 179 | 178 | 176 | 167 | 171 | 174 | 175 | 177 | 173 | 172 |
| 169 | 176 | 178 | 182 | 175 | 172 | 177 | 177 | 179 | 167 |
| 168 | 173 | 167 | 178 | 175 | 167 | 160 | 177 | 182 | 179 |
| 168 | 176 | 177 | 176 | 168 | 168 | 171 | 183 | 168 | 175 |
| 175 | 159 | 162 | 173 | 181 | 179 | 166 | 170 | 178 | 177 |
| 167 | 167 | 171 | 184 | 173 | 176 | 175 | 167 | 167 | 174 |
| 181 | 181 | 172 | 173 | 178 | 182 | 173 | 166 | 174 | 188 |
| 168 | 177 | 170 | 165 | 164 | 176 | 181 | 189 | 168 | 175 |
| 179 | 187 | 168 | 171 | 173 | 190 | 169 | 177 | 170 | 161 |
| 165 | 181 | 179 | 185 | 170 | 178 | 178 | 183 | 169 | 173 |
| 173 | 186 | 172 | 177 | 172 | 164 | 168 | 182 | 184 | 185 |
| 173 | 179 | 181 | 185 | 173 | 173 | 173 | 187 | 179 | 175 |
| 173 | 170 | 177 | 178 | 184 | 185 | 174 | 177 | 180 | 183 |
| 167 | 168 | 171 | 189 | 178 | 177 | 172 | 170 | 176 | 181 |
| 182 | 185 | 176 | 179 | 179 | 182 | 173 | 170 | 173 | 190 |
Полигон частот представляет собой линию с резкими изломами. Для анализа результатов желательно уменьшить число интервалов путём объединения ближайших значений признака. При этом полагают, что оптимальное количество интервалов колеблется от 6-ти до 20-ти. Действуя указанным способом, имеем интервальный ряд распределения, который приведен в табл.2.3.
Рассмотрим способ вычисления средней арифметической и дисперсии с помощью условной средней.
В качестве условной средней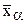 
выбирают середину интервала с наибольшей частотой. Затем вычисляют разности между серединами интервалов и условной средней и делят их на ширину интервала d. В нашем случае 
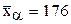; ширина интервала d=3 [MПa].
Средняя арифметическая и дисперсия следующие:
; 
.
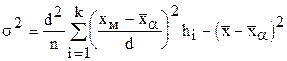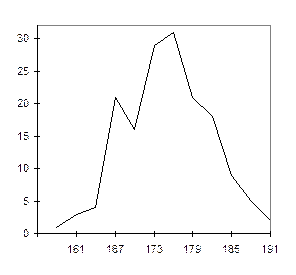
На фиг. 2.2,а представлен полигон частот интервального ряда распределения. Здесь частоты относятся к серединам интервалов.
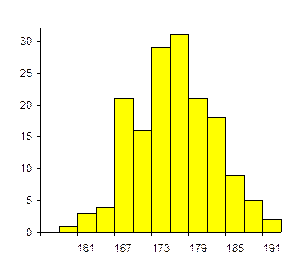
Вместо полигона частот часто вычерчивают ступенчатую кривую, называемую гистограммой. Для этого на интервалах, отложенных по оси абсцисс, строят прямоугольники, высота которых пропорциональна частотам интервалов.
Гистограмма рассматриваемого интервального ряда изображена на фиг.2.2,б.
Таблица 2.3
Упорядоченный ряд наблюдений, составленный по результатам 160-ти
измерений предела текучести прутков
| частота,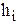 
|
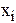
| частота,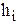
|
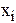
| частота,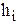
| 
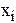
| частота,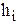
|
| 159 | 1 | 167 | 9 | 175 | 9 | 183 | 5 |
| 160 | 1 | 168 | 10 | 176 | 8 | 184 | 3 |
| 161 | 1 | 169 | 3 | 177 | 14 | 185 | 5 |
| 162 | 1 | 170 | 7 | 178 | 10 | 186 | 1 |
| 163 | 171 | 6 | 179 | 10 | 187 | 2 | |
| 164 | 2 | 172 | 6 | 180 | 1 | 188 | 1 |
| 165 | 2 | 173 | 17 | 181 | 7 | 189 | 2 |
| 166 | 2 | 174 | 6 | 182 | 6 | 190 | 2 |
Сумма 166
|
|
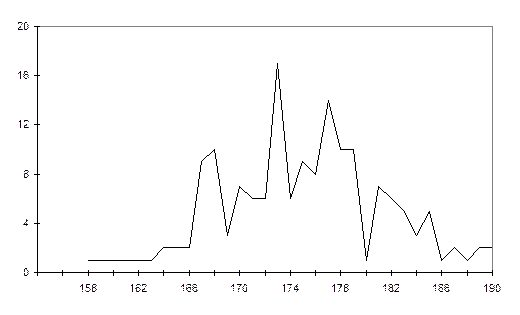
Фиг.2.1. Полигон частот предела текучести алюминиевых прутков.
|
|
|
|
а) б)
Фиг.2.2. Полигон частот (a) и гистограмма частот (б) интервального ряда распределения
Таблица 2.4
Интервальный ряд распределения (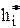 
- теоретическая частота)
| Интервалы | Середина
интервала
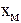
| Частота
;
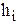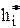
| Относительная частота % | Накопленная частота | Относительная накопленная частота |
| 156,5-159,4 | 158 | 1; 1 | 0,6 | 1 | 0,6 |
| 159,5-162,4 | 161 | 3; 3 | 1,9 | 4 | 2,5 |
| 162,5-165,4 | 164 | 4; 7 | 2,5 | 8 | 5,0 |
| 165,5-168,4 | 167 | 21; 14 | 13,1 | 29 | 18,1 |
| 168,5-171,4 | 170 | 16; 22 | 10,0 | 45 | 28,1 |
| 171,5-174,4 | 173 | 29; 28 | 18,1 | 74 | 46,2 |
| 174,5-177,4 | 176 | 31; 29 | 19,4 | 105 | 65,6 |
| 177,5-180,4 | 179 | 21; 25 | 13,1 | 126 | 78,7 |
| 180,5-183,4 | 182 | 18; 17 | 11,3 | 144 | 90,0 |
| 183,5-186,4 | 185 | 9; 9 | 5,6 | 153 | 95,6 |
| 186,5-189,4 | 188 | 5; 4 | 3,1 | 158 | 98,7 |
| 189,5-192,4 | 191 | 2; 1 | 1,3 | 160 | 100,0 |
Нормальное распределение
Для основательного изучения вопроса рекомендуется учебное пособие: Гмурман В. Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 1972. -368 с.
Напомним, что меру объективной возможности того, что произойдёт событие А, называют его вероятностью Р(А). Если провести N испытаний и определить количество К исходов с осуществлением события А, то величина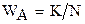 
будет частностью, которая является оценкой вероятности Р(А).
Дискретная случайная величина задаётся перечнем её возможных значений и их вероятностей. Такой способ задания не является общим, так как его нельзя применить для непрерывных случайных величин.
С целью задания любых типов случайных величин вводят интегральные и дифференциальные функции распределения.
Пусть х - действительное число. Вероятность события, состоящего в том, что случайная величина Х примет значение меньше х обозначим через F(x). Тогда интегральной функцией распределения называют функцию F(x), определяющую для каждого значения х вероятность того, что случайная величина Х примет значение меньше х, т.е.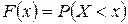 
. Полученное равенство можно истолковать так: F(x) есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.
Случайная величина непрерывна, если её интегральная функция распределения F(x) непрерывно дифференцируема.
Из определения интегральной функции как вероятности вытекают следующие свойства: значения интегральной функции принадлежат отрезку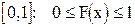 
; F(x) - неубывающая функция, т.е. 
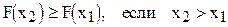; если возможные значения случайной величины принадлежат интервалу 
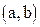, то:
| F(x)=0 | при |  ;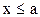
| F(x)=1 | при |  .
|
Следствия: вероятность того, что случайная величина примет значение, заключённое в интервале 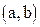, равна приращению интегральной функции на этом интервале, т.е. 
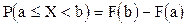; вероятность того, что непрерывная случайная величина Х примет одно определённое значение, равна нулю; если возможные значения непрерывной случайной величины расположены на всей оси х, то справедливы следующие предельные соотношения: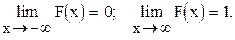 
Функцию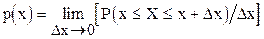 
где P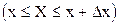 
- вероятность попадания случайной величины Х в интервал 
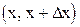называем плотностью распределения непрерывной случайной величины.
Дифференциальной функцией распределения f(x) (или плотностью вероятности р(х)) является первая производная от интегральной функции, т.е. 
. Следовательно, интегральная функция это первообразная для соответствующей дифференциальной функции.
Теорема. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (а,b), следующая:
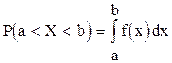
Результат теоремы означает: вероятность того, что непрерывная случайная величина принимает значение, принадлежащее интервалу (a, b), равна площади криволинейной трапеции, ограниченной осью х, кривой распределения f(x) и прямыми x=a и х=b.
Пример. Дана дифференциальная функция случайной величины Х:
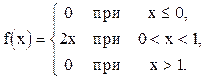
Найти вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0,5; 1).
Р е ш е н и е. Искомая вероятность:
.
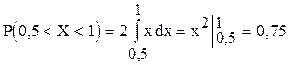Дифференциальная функция распределения вероятности непрерывной случайной величины имеет следующие свойства:
1) дифференциальная функция неотрицательна, т.е. f(x)0;
2) несобственный интеграл от дифференциальной функции:
;
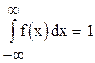3) дифференциальная функция определяет плотность распределения вероятности для каждой точки х.
Из последнего свойства следует: вероятность того, что случайная величина принадлежит интервалу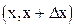 
, приближённо равна площади прямоугольника с основанием Dx и высотой f(x).
Распределением случайных величин называют совокупность значений этих величин, расположенных в возрастающем порядке. Центр распределения характеризуется математическим ожиданием.
Эмпирическим называют распределение относительных частот. Эмпирические распределения изучает математическая статистика.
Теоретическим называют распределение вероятностей. Такие распределения изучает теория вероятностей.
Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [f,b], называют определённый интеграл:
.
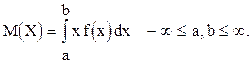Математическое ожидание в инженерной практике оценивают средним значением результатов наблюдений.
Дисперсией непрерывной случайной величины называют математическое ожидание квадрата её отклонения, т.е.:
. 
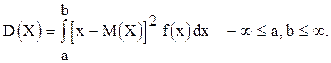
Для среднего квадратичного отклонения имеем:
.
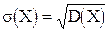Симметрия рассеивания случайной величины характеризуется асимметрией. Для дискретных наблюдений:
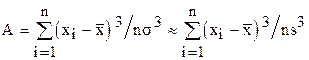
Эксцесс (для дискретных наблюдений):
.
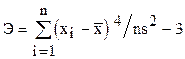Асимметрия положительна (А>0), если длинная часть кривой распределения лежит справа от математического ожидания и отрицательная в противном случае. Если эксцесс некоторого распределения отличается от нуля и положительный (Э > 0), то кривая имеет более высокую и острую вершину и наоборот.
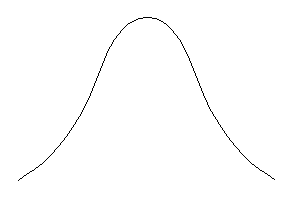
Известен ряд законов распределения непрерывных случайных величин: логарифмическое нормальное, полунормальное, гамма-распределение, бета-распределение и др. Центральное место среди законов распределения занимает нормальный закон распределения. Нормальным (распределением Гаусса) является распределение вероятностей случайной величины, которое описывается функцией:
.
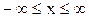Для нормального распределения асимметрия и эксцесс равны нулю.
Исследование функции нормального распределения методами математического анализа приводит к следующим результатам: функция определена на всей оси х; при всех значениях х функция принимает положительные значения; ось х служит горизонтальной осью графика функции; при х=а функция имеет максимум, равный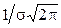 
; график функции симметричен относительно прямой х=а; точки графика 
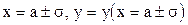являются точками перегиба.
Математическое ожидание нормального распределения равно параметру а; среднее квадратичное отклонение этого распределения равно параметру s.
Почему нормально распределённые случайные величины широко распространены на практике? Ответ на вопрос дан математиком А.М. Ляпуновым при доказательстве центральной предельной теоремы теории вероятностей. .Здесь ограничимся следствием из названной теоремы.
Если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждого из которых на всю сумму ничтожно мало, то Х имеет распределение близкое к нормальному.
Пример. Пусть производится измерение некоторого параметра. Любое измерение даёт приближённое значение измеряемой величины, так как на результат оказывают влияние многие независимые случайные факторы (температура, электромагнитные поля, влажность, колебания прибора и др.). Каждый из этих факторов порождает "частную ошибку". Совокупность факторов порождает суммарную ошибку. Рассматривая суммарную ошибку как сумму очень большого числа независимых частных ошибок, можем заключить, что суммарная ошибка имеет нормальное распределение, Это подтверждает опыт.
На практике часто приходится иметь дело с распределением, которое незначительно отличается от нормального (впрочем, отсюда ещё не следует, что нормальное распределение всегда имеет место).
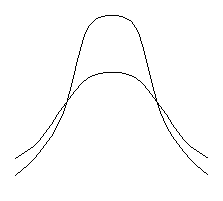
Если изобразить графически нормальные распределения (см. фиг.2.3) с одинаковыми математическими ожиданиями, но с различными средними квадратичными отклонениями, то при меньшем значении s кривая будет падать по обе стороны от вершины более круто, чем при s, имеющей большее значение; с увеличением s кривая становиться более пологой (фиг.2.3,б).
Плотность нормального распределения выражается функцией:
; ,
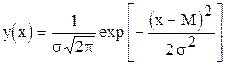где e=2,71828; =3,14159; М и s - математическое ожидание и среднее квадратичное отклонение нормального распределения (являются параметрами распределения).
 |
а) б)
Фиг.2.3. Нормальное распределение (а) и кривые нормального
распределения с различными дисперсиями (б).
Для дальнейшего использования таблиц математической статистики, осуществим замену переменной. Пусть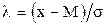 
. Тогда
,
где j - плотность нормированного нормального распределения; d - ширина интервала.
Вычисления площади под кривой нормального распределения показывает, что эта площадь всегда равна единице. В связи с этим свойством, площадь, ограниченная ординатами в точках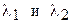 
, представляет собой относительную частоту или вероятность попадания значений признака х в интервал 
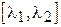(в интервал 
).
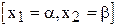Если случайная величина Х задана дифференциальной функцией, то вероятность того, что Х примет значение, принадлежащее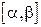 
такова:
.
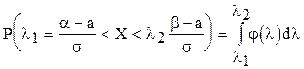Пользуясь функцией Лапласа 
(табл.1, Приложение), имеем:
.
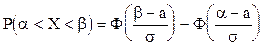С помощью введенных формул легко вычислить теоретические значения частот нормального распределения с любым математическим ожиданием и средним квадратичным отклонением.
Пример. Случайная величина Х распределена по нормальному закону. Математическое ожидание и среднее квадратичное отклонение этой величины соответственно равны 30 и 10. Найти вероятность того, что Х примет значение, принадлежащее интервалу (10, 50).
Р е ш е н и е. По условию a=10, b=50, а=30, s=10, следовательно,
.
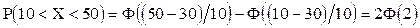По табл. значений функции Лапласа находим Ф(х=2)=0,4772. Отсюда искомая вероятность Р(10<X<50)=20,4772=0,9544.
Правило трёх сигм. Между границами находится 99,73% всех наблюдений, т.е. практически все значения. Поэтому принимают следующее утверждение: если какое-либо значение появляется за пределами трёхсигмового участка, то оно является случайным.
На основании правила трёх сигм после вычисления асимметрии и эксцесса можно проверитьподчиняются ли изучаемые наблюдения нормальному закону. Для этого проверяются условия:
.
Если эти условия выполняются, то считают, что наблюдения подчиняются нормальному закону.
Дата: 2019-05-29, просмотров: 280.
