УНИВЕРСИТЕТ (УГТУ-УПИ)
ПЛАНИРОВАНИЕ
ЭКСПЕРИМЕНТА
ВВЕДЕНИЕ
Эксперименты по своей постановке и способам проведения могут быть пассивными и активными. В ходе пассивного эксперимента исследователь наблюдает за процессом, не вмешиваясь в его протекание, а затем, по окончании процесса, применяет математические методы для обработки результатов.
Активные эксперименты проводятся в соответствии с такой схемы постановки опытов, которая предусматривает определённую последовательность изменения влияющих факторов, формализацию априорных сведений, имеющихся в начале эксперимента, и применение ряда приёмов, которые в целом и называются планированием эксперимента.
При планировании и выполнении экспериментального исследования перед исследователем, как правило, возникают две задачи: задача математического описания объекта исследования и задача оптимизации. Решение этих задач связано с необходимостью предварительной разработки математической модели объекта исследования, проверки её адекватности объекту с учётом действия случайных возмущений и определение области применения. Таким образом, теория планирования эксперимента неразрывно связана с теорией подобия и моделирования. С целью учёта влияния на результаты эксперимента случайных факторов в ходе его планирования и обработки массива экспериментальных данных широко используются методы математической статистики.
Задача данного курса состоит в том, чтобы ввести читателя в методологию экспериментальных исследований, которая объединяет методы математической статистики, теорию подобия и моделирования и теорию планирования эксперимента.
1.1. Необходимость планирования эксперимента
В качестве примера сравнительно простого эксперимента рассмотрим одноосное растяжение (сжатие) в изотермических условиях металлического образца цилиндрической формы.
Схема установки для механических испытаний показана на фиг. 1.1. Испытуемый образец 1 помещён в захваты 2 растяжной машины 3. Образец нагревается пропусканием через него электрического тока от устройства 4. Для защиты образца от окисления он вместе с захватами помещён в камеру 5 с защитной атмосферой, подаваемой устройством 6. Кроме того экспериментальная установка оснащена силоизмерительным устройством 7, устройством 8 для измерения перемещений захватов испытательной машины и устройством 9 для измерения температуры образца.
Для сбора и обработки информации относительно изменений температуры , силы P растяжения, перемещения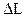 
и скорости перемещения 
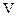захватов установка оснащена устройством сопряжения 10, вычислительной машиной 11 и графопостроителем 12. Так как все 12 элементов (при дальнейшей детализации их может быть больше) связаны между собой и взаимодействуют друг с другом, то экспериментальная установка представляет собой достаточно сложную для исследования систему.
Для растяжения образца к нему необходимо приложить силовое воздействие P, действующее вдоль оси симметрии, в результате чего в нём возникают напряжения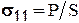 
и деформации 
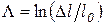, величина которых зависит от перемещения захватов испытательной машины. Здесь S - площадь поперечного сечения образца; обозначает степень деформации в текущий момент испытания; 
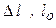- изменение длины и длина рабочей части образца.
 |
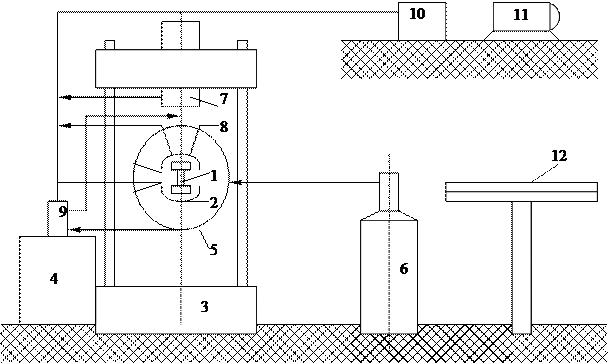Фиг.1.1. Схема установки для механических испытаний образцов:
1- образец; 2- захваты; 3- растяжная машина; 4- устройство нагрева;
5- камера для защитной атмосферы; 6- баллоны с газом;
7- силоизмеритель; 8- измеритель деформации; 9- термопара;
10- устройство сопряжения; 11- ЭВМ; 12- графопостроитель.
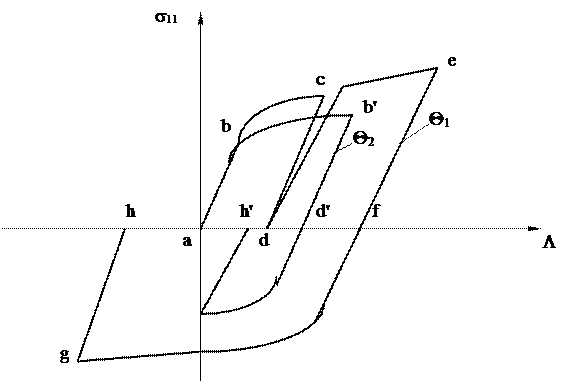
Фиг.1.2. Диаграмма одноосного растяжения (сжатия) образца.
В ходе испытания графопостроитель рисует диаграмму растяжения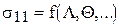 
(фиг. 2). Многоточие в приведенной функции показывает факторы, не принятые в рассмотрение. В числе этих факторов скорости перемещения захватов, определяющие скорости деформаций, неоднородное распределение деформаций, систематические ошибки измерений, например, связанные с деформацией элементов конструкции испытательной машины, а также случайные факторы.
Диаграмма растяжения показана на фиг.1.2. Из курса "сопротивление материалов" известно, что различные участки этой диаграммы характеризуют следующие процессы: ab - растяжение в упругой области; bc - упругопластическая деформация; сd и ef - упругая разгрузка; ad - остаточная (пластическая) деформация; de - повторное упругопластическое растяжение; fg - упругопластическое сжатие; ab'd'e' - растяжение и сжатие при повышенной температуре, в условиях когда в образце проявляются свойства вязкопластичности.
Из диаграммы растяжения (сжатия), приведенной на фиг 1.2. видно, что исследуемый процесс далеко не тривиальный. Чтобы разобраться в этом процессе, желательно иметь математическую модель испытуемого образца. Для разработки такой модели целесообразно использовать подход механики деформируемого твёрдого тела.
Известно, что металлические материалы сочетают в себе упругие, пластические и вязкие свойства, т.е. являются в общем случае упруго-вязкопластическими. Следовательно, математическая модель образца для механических испытаний можно представить в виде соединения (комбинации) упругих, вязких и пластических элементов.
В соответствии с методологией решения задач механики процесс деформирования образца разделим на малые этапы так, что имеем лишь малые (покомпонентно) градиенты перемещений. При этом этапу нагружения с номером n соответствует промежуток времени:
.
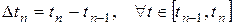На каждом этапе ведётся расчёт напряжённого состояния в интересующих частицах деформируемого тела, после чего осуществляется численное интегрирование по времени.
Для решения нестационарных задач указанным способом обычно используют теорию течения.
В соответствии с теорией течения полагаем, что скорости деформаций при растяжении образца представляют собой аддитивную сумму скоростей упругой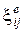 
, вязкой 
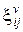, пластической деформации 
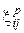и температурного расширения 
:
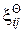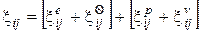, (1.1)
Ограничиваясь линейными соотношениями для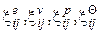 
, в упругой области в соответствии с законом Гука имеем: 
;
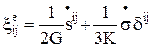для линейной вязкости - закон Ньютона: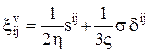 
;
для пластического течения - закон Мизеса: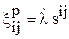 
;
для температурного расширения (сжатия):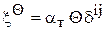 
,
где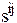 
- компоненты девиатора напряжений; 
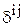- символ Кронекера; 
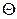- температура; G - модуль сдвига ( 
, 
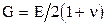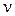- коэффициент Пуассона, E - модуль Юнга); K - модуль всестороннего сжатия ( 
); 
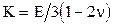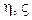- первый и второй коэффициенты вязкости; 
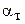- коэффициент линейного термического расширения; - пластический модуль; 
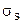- предел текучести при растяжении ( 
); 
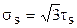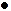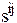- над и обозначает производную по времени. Параметры G, K (или E, ), 
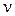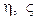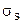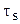, (или 
) и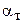 
являются функциями температуры .
Исходя из физического смысла задачи, на основании (1.1) имеем:
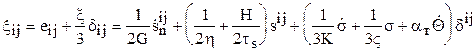, (1.2)
где индекс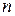 
показывает, что соответствующие параметры рассчитаны на начальный момент очередного этапа нагружения.
Предложенная модель (уравнение (1.2)) испытуемого образца содержит, по крайней мере, 5 параметров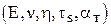 
, которые требуется определить экспериментальным путём. Это, как показывает практика, является весьма трудоёмким делом. Если изучать зависимость "напряжение - деформация" не привлекая методов планирования эксперимента, которые будут рассмотрены ниже, то потребуется много опытов и материальных затрат.
На результат любого эксперимента оказывает влияние множество случайных факторов (разброс механических свойств образцов, неконтролируемые деформации несущих элементов конструкции, колебания фундамента, вибрации упругих элементов испытательной машины, изменение температуры окружающей среды и т. д.). Чтобы применить методы математической статистики, необходимо каждый опыт повторить несколько раз. При этом требуемое количество экспериментальных точек и, соответственно, трудовые затраты растут.
Необходимость уменьшать количество опытов и повышать точность эксперимента привели к возникновению дисциплины, которую называют планирование эксперимента.
Ошибки эксперимента
В контролируемом эксперименте влияние внешних переменных исключено и независимые переменные можно изменять в точности по желанию исследователя. Проведение контролируемого эксперимента или изоляция его от окружающих условий является одним из основных принципов научного исследования.
Заметим, что термин переменная означает любую варьируемую физическую величину. Если варьирование переменной осуществляется независимо от других величин, то её называем независимой переменной.
Если некоторая величина, оказывающая влияние на эксперимент, изменяется случайным образом и её нельзя контролировать, то она является внешней переменной.
При проведении любых экспериментов натурных или физических исследователь сталкивается с тем обстоятельством, что все параметры объекта исследования (системы-оригинала), равно как и параметры моделей объекта, могут быть определены лишь с некоторой точностью.
Измерения переменных осуществляются с помощью приборов. Они дают некоторые ошибки: систематические и случайные. Систематические ошибки можно определить для каждого конкретного измерительного устройства.
Случайная ошибка не имеет фиксированного значения, подобно систематической ошибке; она будет различной при каждом повторном снятии отсчёта. Статистические методы обработки экспериментальных данных позволяют для каждого прибора определить средние значения случайных ошибок.
Наряду с ошибками измерений возможно искажение информации в каналах связи.
При проведении эксперимента можно ничего не знать о характере ошибок, кроме того, что следует ожидать некоторого отклонения от точного значения. В этом случае экспериментатор имеет дело с неопределённостью. Необходимо вычислить или, что более вероятно, угадать эту неопределённость.
Никогда нельзя установить абсолютную величину случайной ошибки. Для исследования случайных ошибок необходимо многократное повторение опытов и применение методов математической статистики.
Теория эксперимента предполагает, что во всех опытах случайные ошибки неизбежны. Этот факт должен учитываться при планировании каждого эксперимента.
Основные понятия теории эксперимента
Эксперимент занимает значительное место в научных работах. Однако, возникает вопрос насколько эффективно он используется. Здесь результат не утешительный. В ряде случаев экспериментальные исследования организуются и проводятся настолько хаотично, что их коэффициент полезного действия оценивается величиной, не превышающей нескольких процентов. Повышение эффективности научных исследований достигается благодаря теории эксперимента.
Теория эксперимента содержит ряд концепций, которые обеспечивают успешную реализацию задач исследования. К ним относятся концепции рандомизации, последовательного эксперимента, математического моделирования, оптимального использования факторного пространства и др.
Каким бы простым изначально не казалось экспериментальное исследование, прежде всего, необходимо составить план эксперимента.
В процессе эксперимента важную роль играет обнаружение неполадок, если рассматриваются неполадки в самом широком смысле. С этой задачей непосредственно связана проверка приемлемости полученных результатов. Наконец, для любого эксперимента необходим анализ результатов и их интерпретация.
План эксперимента - это общий термин. Он определяет набор инструкций по проведению эксперимента, в которых указываются последовательность работы, характер и величина изменений переменных и даются указания о проведении повторных опытов.
Принцип рандомизации заключается в том, что в план эксперимента вводят элемент случайности. Для этого план эксперимента составляется таким образом, чтобы систематические факторы, которые трудно поддаются контролю, учитывались статистически и затем исключались из результатов как систематические ошибки.
Последовательность проведения эксперимента означает порядок, в котором вносятся изменения в работу испытательной аппаратуры. При последовательном проведении эксперимент выполняется поэтапно, чтобы результаты каждого этапа можно было проанализировать и принять решение о ходе дальнейшего исследования.
Планирование эксперимента - это процедура выбора условий проведения опытов, необходимых для решения поставленной задачи с требуемой точностью. При этом существенно следующее: стремление к минимизации числа опытов; одновременное варьирование всеми переменными, определяющими процесс, в соответствии с некоторыми специальными алгоритмами; использование математического аппарата, формализующего основные действия экспериментатора; выбор стратегии, позволяющей принимать обоснованные решения после каждой серии опытов.
При планировании эксперимента различаются два основных типа задач: интерполяционные и экстремальные.
Объект исследования - это основное понятие теории эксперимента. Для описания объекта исследования удобно пользоваться представлением о кибернетической системе, которую называют чёрным ящиком. Схема "чёрного ящика" приведена на фиг.1.3.
Для проведения эксперимента необходимо иметь возможность воздействовать на поведение чёрного ящика. Такие воздействия называют входами чёрного ящика или факторами.
Стрелки справа (фиг.1.3) изображают численные характеристики целевых функций, которые называют параметрами оптимизации. Верхняя стрелка обозначает не контролируемые воздействия внешней среды. Нижняя стрелка - управление.
 |
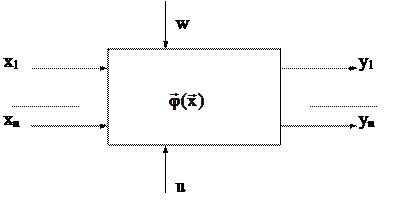Фиг.1.3. Схема “чёрного ящика”.
В п.1.1 показано, что исследователю необходимы математические модели объекта исследования. Моделью называем уравнение, связывающее параметр оптимизации с факторами. Это уравнение в общем виде можно записать так:
,
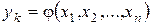где символ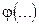 
называется функцией отклика.
Каждый фактор может принимать в опыте одно из нескольких значений. Такие значения называются уровнями.
Фиксированный набор уровней факторов определяет одно из возможных состояний "чёрного ящика". Если перебрать возможные наборы состояний, то получим множество состояний чёрного ящика. Чтобы узнать число состояний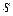 
используется формула 
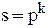, где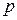 
- число уровней; 
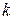- число факторов.
Многофакторный эксперимент может привести к очень большому числу опытов и значительным материальным затратам. Чтобы уменьшить число опытов и применяют планирование эксперимента. При этом требуется воспроизведение на объекте исследование результатов опытов; т. е. необходимо обеспечить адекватность модели реальному объекту. В связи с этим планирование эксперимента должно осуществляться таким образом, чтобы происходила взаимная компенсация случайных ошибок, что должно приводить к повышению точности эксперимента.
Применение планирования эксперимента делает поведение экспериментатора целенаправленным и организованным, существенно повышает производительность труда и надёжность результатов исследования.
Дата: 2019-05-29, просмотров: 175.
