РОССИЙСКАЯ АКАДЕМИЯ НАУК - УРАЛЬСКОЕ ОТДЕЛЕНИЕ
ИНСТИТУТ МАШИНОВЕДЕНИЯ УрО РАН
УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ (УГТУ-УПИ)
ПЛАНИРОВАНИЕ
ЭКСПЕРИМЕНТА
ВВЕДЕНИЕ
Эксперименты по своей постановке и способам проведения могут быть пассивными и активными. В ходе пассивного эксперимента исследователь наблюдает за процессом, не вмешиваясь в его протекание, а затем, по окончании процесса, применяет математические методы для обработки результатов.
Активные эксперименты проводятся в соответствии с такой схемы постановки опытов, которая предусматривает определённую последовательность изменения влияющих факторов, формализацию априорных сведений, имеющихся в начале эксперимента, и применение ряда приёмов, которые в целом и называются планированием эксперимента.
При планировании и выполнении экспериментального исследования перед исследователем, как правило, возникают две задачи: задача математического описания объекта исследования и задача оптимизации. Решение этих задач связано с необходимостью предварительной разработки математической модели объекта исследования, проверки её адекватности объекту с учётом действия случайных возмущений и определение области применения. Таким образом, теория планирования эксперимента неразрывно связана с теорией подобия и моделирования. С целью учёта влияния на результаты эксперимента случайных факторов в ходе его планирования и обработки массива экспериментальных данных широко используются методы математической статистики.
Задача данного курса состоит в том, чтобы ввести читателя в методологию экспериментальных исследований, которая объединяет методы математической статистики, теорию подобия и моделирования и теорию планирования эксперимента.
1.1. Необходимость планирования эксперимента
В качестве примера сравнительно простого эксперимента рассмотрим одноосное растяжение (сжатие) в изотермических условиях металлического образца цилиндрической формы.
Схема установки для механических испытаний показана на фиг. 1.1. Испытуемый образец 1 помещён в захваты 2 растяжной машины 3. Образец нагревается пропусканием через него электрического тока от устройства 4. Для защиты образца от окисления он вместе с захватами помещён в камеру 5 с защитной атмосферой, подаваемой устройством 6. Кроме того экспериментальная установка оснащена силоизмерительным устройством 7, устройством 8 для измерения перемещений захватов испытательной машины и устройством 9 для измерения температуры образца.
Для сбора и обработки информации относительно изменений температуры , силы P растяжения, перемещения 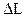 и скорости перемещения
и скорости перемещения 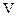 захватов установка оснащена устройством сопряжения 10, вычислительной машиной 11 и графопостроителем 12. Так как все 12 элементов (при дальнейшей детализации их может быть больше) связаны между собой и взаимодействуют друг с другом, то экспериментальная установка представляет собой достаточно сложную для исследования систему.
захватов установка оснащена устройством сопряжения 10, вычислительной машиной 11 и графопостроителем 12. Так как все 12 элементов (при дальнейшей детализации их может быть больше) связаны между собой и взаимодействуют друг с другом, то экспериментальная установка представляет собой достаточно сложную для исследования систему.
Для растяжения образца к нему необходимо приложить силовое воздействие P, действующее вдоль оси симметрии, в результате чего в нём возникают напряжения 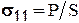 и деформации
и деформации 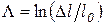 , величина которых зависит от перемещения захватов испытательной машины. Здесь S - площадь поперечного сечения образца; обозначает степень деформации в текущий момент испытания;
, величина которых зависит от перемещения захватов испытательной машины. Здесь S - площадь поперечного сечения образца; обозначает степень деформации в текущий момент испытания; 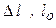 - изменение длины и длина рабочей части образца.
- изменение длины и длина рабочей части образца.
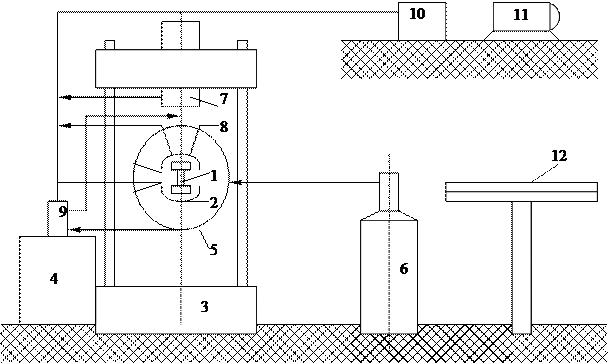 |
Фиг.1.1. Схема установки для механических испытаний образцов:
1- образец; 2- захваты; 3- растяжная машина; 4- устройство нагрева;
5- камера для защитной атмосферы; 6- баллоны с газом;
7- силоизмеритель; 8- измеритель деформации; 9- термопара;
10- устройство сопряжения; 11- ЭВМ; 12- графопостроитель.
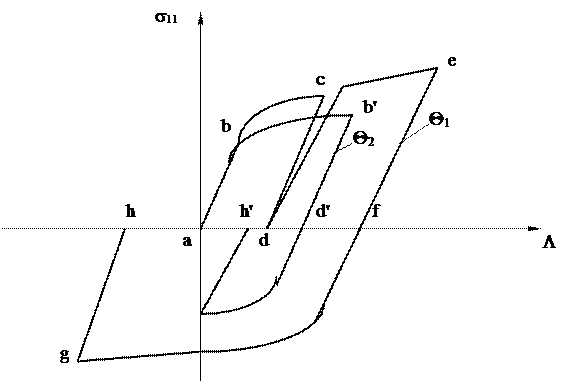
Фиг.1.2. Диаграмма одноосного растяжения (сжатия) образца.
В ходе испытания графопостроитель рисует диаграмму растяжения 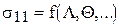 (фиг. 2). Многоточие в приведенной функции показывает факторы, не принятые в рассмотрение. В числе этих факторов скорости перемещения захватов, определяющие скорости деформаций, неоднородное распределение деформаций, систематические ошибки измерений, например, связанные с деформацией элементов конструкции испытательной машины, а также случайные факторы.
(фиг. 2). Многоточие в приведенной функции показывает факторы, не принятые в рассмотрение. В числе этих факторов скорости перемещения захватов, определяющие скорости деформаций, неоднородное распределение деформаций, систематические ошибки измерений, например, связанные с деформацией элементов конструкции испытательной машины, а также случайные факторы.
Диаграмма растяжения показана на фиг.1.2. Из курса "сопротивление материалов" известно, что различные участки этой диаграммы характеризуют следующие процессы: ab - растяжение в упругой области; bc - упругопластическая деформация; сd и ef - упругая разгрузка; ad - остаточная (пластическая) деформация; de - повторное упругопластическое растяжение; fg - упругопластическое сжатие; ab'd'e' - растяжение и сжатие при повышенной температуре, в условиях когда в образце проявляются свойства вязкопластичности.
Из диаграммы растяжения (сжатия), приведенной на фиг 1.2. видно, что исследуемый процесс далеко не тривиальный. Чтобы разобраться в этом процессе, желательно иметь математическую модель испытуемого образца. Для разработки такой модели целесообразно использовать подход механики деформируемого твёрдого тела.
Известно, что металлические материалы сочетают в себе упругие, пластические и вязкие свойства, т.е. являются в общем случае упруго-вязкопластическими. Следовательно, математическая модель образца для механических испытаний можно представить в виде соединения (комбинации) упругих, вязких и пластических элементов.
В соответствии с методологией решения задач механики процесс деформирования образца разделим на малые этапы так, что имеем лишь малые (покомпонентно) градиенты перемещений. При этом этапу нагружения с номером n соответствует промежуток времени:
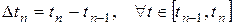 .
.
На каждом этапе ведётся расчёт напряжённого состояния в интересующих частицах деформируемого тела, после чего осуществляется численное интегрирование по времени.
Для решения нестационарных задач указанным способом обычно используют теорию течения.
В соответствии с теорией течения полагаем, что скорости деформаций при растяжении образца представляют собой аддитивную сумму скоростей упругой 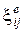 , вязкой
, вязкой 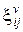 , пластической деформации
, пластической деформации 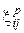 и температурного расширения
и температурного расширения 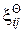 :
:
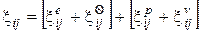 , (1.1)
, (1.1)
Ограничиваясь линейными соотношениями для 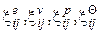 , в упругой области в соответствии с законом Гука имеем:
, в упругой области в соответствии с законом Гука имеем: 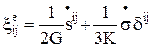 ;
;
для линейной вязкости - закон Ньютона: 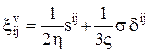 ;
;
для пластического течения - закон Мизеса: 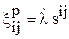 ;
;
для температурного расширения (сжатия): 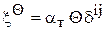 ,
,
где 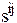 - компоненты девиатора напряжений;
- компоненты девиатора напряжений; 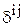 - символ Кронекера;
- символ Кронекера; 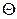 - температура; G - модуль сдвига (
- температура; G - модуль сдвига ( 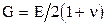 ,
, 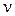 - коэффициент Пуассона, E - модуль Юнга); K - модуль всестороннего сжатия (
- коэффициент Пуассона, E - модуль Юнга); K - модуль всестороннего сжатия ( 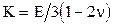 );
); 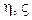 - первый и второй коэффициенты вязкости;
- первый и второй коэффициенты вязкости; 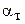 - коэффициент линейного термического расширения; - пластический модуль;
- коэффициент линейного термического расширения; - пластический модуль; 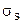 - предел текучести при растяжении (
- предел текучести при растяжении ( 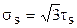 );
); 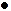 - над
- над 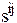 и обозначает производную по времени. Параметры G, K (или E,
и обозначает производную по времени. Параметры G, K (или E, 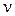 ),
), 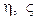 ,
, 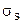 (или
(или 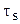 ) и
) и 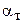 являются функциями температуры .
являются функциями температуры .
Исходя из физического смысла задачи, на основании (1.1) имеем:
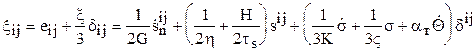 , (1.2)
, (1.2)
где индекс 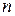 показывает, что соответствующие параметры рассчитаны на начальный момент очередного этапа нагружения.
показывает, что соответствующие параметры рассчитаны на начальный момент очередного этапа нагружения.
Предложенная модель (уравнение (1.2)) испытуемого образца содержит, по крайней мере, 5 параметров 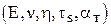 , которые требуется определить экспериментальным путём. Это, как показывает практика, является весьма трудоёмким делом. Если изучать зависимость "напряжение - деформация" не привлекая методов планирования эксперимента, которые будут рассмотрены ниже, то потребуется много опытов и материальных затрат.
, которые требуется определить экспериментальным путём. Это, как показывает практика, является весьма трудоёмким делом. Если изучать зависимость "напряжение - деформация" не привлекая методов планирования эксперимента, которые будут рассмотрены ниже, то потребуется много опытов и материальных затрат.
На результат любого эксперимента оказывает влияние множество случайных факторов (разброс механических свойств образцов, неконтролируемые деформации несущих элементов конструкции, колебания фундамента, вибрации упругих элементов испытательной машины, изменение температуры окружающей среды и т. д.). Чтобы применить методы математической статистики, необходимо каждый опыт повторить несколько раз. При этом требуемое количество экспериментальных точек и, соответственно, трудовые затраты растут.
Необходимость уменьшать количество опытов и повышать точность эксперимента привели к возникновению дисциплины, которую называют планирование эксперимента.
Ошибки эксперимента
В контролируемом эксперименте влияние внешних переменных исключено и независимые переменные можно изменять в точности по желанию исследователя. Проведение контролируемого эксперимента или изоляция его от окружающих условий является одним из основных принципов научного исследования.
Заметим, что термин переменная означает любую варьируемую физическую величину. Если варьирование переменной осуществляется независимо от других величин, то её называем независимой переменной.
Если некоторая величина, оказывающая влияние на эксперимент, изменяется случайным образом и её нельзя контролировать, то она является внешней переменной.
При проведении любых экспериментов натурных или физических исследователь сталкивается с тем обстоятельством, что все параметры объекта исследования (системы-оригинала), равно как и параметры моделей объекта, могут быть определены лишь с некоторой точностью.
Измерения переменных осуществляются с помощью приборов. Они дают некоторые ошибки: систематические и случайные. Систематические ошибки можно определить для каждого конкретного измерительного устройства.
Случайная ошибка не имеет фиксированного значения, подобно систематической ошибке; она будет различной при каждом повторном снятии отсчёта. Статистические методы обработки экспериментальных данных позволяют для каждого прибора определить средние значения случайных ошибок.
Наряду с ошибками измерений возможно искажение информации в каналах связи.
При проведении эксперимента можно ничего не знать о характере ошибок, кроме того, что следует ожидать некоторого отклонения от точного значения. В этом случае экспериментатор имеет дело с неопределённостью. Необходимо вычислить или, что более вероятно, угадать эту неопределённость.
Никогда нельзя установить абсолютную величину случайной ошибки. Для исследования случайных ошибок необходимо многократное повторение опытов и применение методов математической статистики.
Теория эксперимента предполагает, что во всех опытах случайные ошибки неизбежны. Этот факт должен учитываться при планировании каждого эксперимента.
Основные понятия теории эксперимента
Эксперимент занимает значительное место в научных работах. Однако, возникает вопрос насколько эффективно он используется. Здесь результат не утешительный. В ряде случаев экспериментальные исследования организуются и проводятся настолько хаотично, что их коэффициент полезного действия оценивается величиной, не превышающей нескольких процентов. Повышение эффективности научных исследований достигается благодаря теории эксперимента.
Теория эксперимента содержит ряд концепций, которые обеспечивают успешную реализацию задач исследования. К ним относятся концепции рандомизации, последовательного эксперимента, математического моделирования, оптимального использования факторного пространства и др.
Каким бы простым изначально не казалось экспериментальное исследование, прежде всего, необходимо составить план эксперимента.
В процессе эксперимента важную роль играет обнаружение неполадок, если рассматриваются неполадки в самом широком смысле. С этой задачей непосредственно связана проверка приемлемости полученных результатов. Наконец, для любого эксперимента необходим анализ результатов и их интерпретация.
План эксперимента - это общий термин. Он определяет набор инструкций по проведению эксперимента, в которых указываются последовательность работы, характер и величина изменений переменных и даются указания о проведении повторных опытов.
Принцип рандомизации заключается в том, что в план эксперимента вводят элемент случайности. Для этого план эксперимента составляется таким образом, чтобы систематические факторы, которые трудно поддаются контролю, учитывались статистически и затем исключались из результатов как систематические ошибки.
Последовательность проведения эксперимента означает порядок, в котором вносятся изменения в работу испытательной аппаратуры. При последовательном проведении эксперимент выполняется поэтапно, чтобы результаты каждого этапа можно было проанализировать и принять решение о ходе дальнейшего исследования.
Планирование эксперимента - это процедура выбора условий проведения опытов, необходимых для решения поставленной задачи с требуемой точностью. При этом существенно следующее: стремление к минимизации числа опытов; одновременное варьирование всеми переменными, определяющими процесс, в соответствии с некоторыми специальными алгоритмами; использование математического аппарата, формализующего основные действия экспериментатора; выбор стратегии, позволяющей принимать обоснованные решения после каждой серии опытов.
При планировании эксперимента различаются два основных типа задач: интерполяционные и экстремальные.
Объект исследования - это основное понятие теории эксперимента. Для описания объекта исследования удобно пользоваться представлением о кибернетической системе, которую называют чёрным ящиком. Схема "чёрного ящика" приведена на фиг.1.3.
Для проведения эксперимента необходимо иметь возможность воздействовать на поведение чёрного ящика. Такие воздействия называют входами чёрного ящика или факторами.
Стрелки справа (фиг.1.3) изображают численные характеристики целевых функций, которые называют параметрами оптимизации. Верхняя стрелка обозначает не контролируемые воздействия внешней среды. Нижняя стрелка - управление.
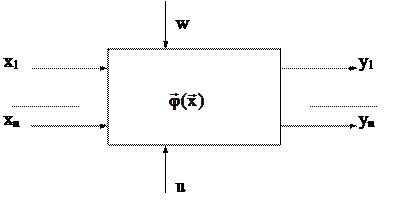 |
Фиг.1.3. Схема “чёрного ящика”.
В п.1.1 показано, что исследователю необходимы математические модели объекта исследования. Моделью называем уравнение, связывающее параметр оптимизации с факторами. Это уравнение в общем виде можно записать так:
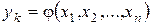 ,
,
где символ 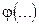 называется функцией отклика.
называется функцией отклика.
Каждый фактор может принимать в опыте одно из нескольких значений. Такие значения называются уровнями.
Фиксированный набор уровней факторов определяет одно из возможных состояний "чёрного ящика". Если перебрать возможные наборы состояний, то получим множество состояний чёрного ящика. Чтобы узнать число состояний 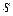 используется формула
используется формула 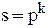 , где
, где 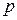 - число уровней;
- число уровней; 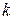 - число факторов.
- число факторов.
Многофакторный эксперимент может привести к очень большому числу опытов и значительным материальным затратам. Чтобы уменьшить число опытов и применяют планирование эксперимента. При этом требуется воспроизведение на объекте исследование результатов опытов; т. е. необходимо обеспечить адекватность модели реальному объекту. В связи с этим планирование эксперимента должно осуществляться таким образом, чтобы происходила взаимная компенсация случайных ошибок, что должно приводить к повышению точности эксперимента.
Применение планирования эксперимента делает поведение экспериментатора целенаправленным и организованным, существенно повышает производительность труда и надёжность результатов исследования.
Нормальное распределение
Для основательного изучения вопроса рекомендуется учебное пособие: Гмурман В. Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 1972. -368 с.
Напомним, что меру объективной возможности того, что произойдёт событие А, называют его вероятностью Р(А). Если провести N испытаний и определить количество К исходов с осуществлением события А, то величина 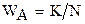 будет частностью, которая является оценкой вероятности Р(А).
будет частностью, которая является оценкой вероятности Р(А).
Дискретная случайная величина задаётся перечнем её возможных значений и их вероятностей. Такой способ задания не является общим, так как его нельзя применить для непрерывных случайных величин.
С целью задания любых типов случайных величин вводят интегральные и дифференциальные функции распределения.
Пусть х - действительное число. Вероятность события, состоящего в том, что случайная величина Х примет значение меньше х обозначим через F(x). Тогда интегральной функцией распределения называют функцию F(x), определяющую для каждого значения х вероятность того, что случайная величина Х примет значение меньше х, т.е. 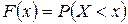 . Полученное равенство можно истолковать так: F(x) есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.
. Полученное равенство можно истолковать так: F(x) есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки х.
Случайная величина непрерывна, если её интегральная функция распределения F(x) непрерывно дифференцируема.
Из определения интегральной функции как вероятности вытекают следующие свойства: значения интегральной функции принадлежат отрезку 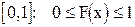 ; F(x) - неубывающая функция, т.е.
; F(x) - неубывающая функция, т.е. 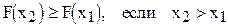 ; если возможные значения случайной величины принадлежат интервалу
; если возможные значения случайной величины принадлежат интервалу 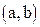 , то:
, то:
| F(x)=0 | при | 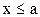 ; ;
| F(x)=1 | при | 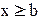 . .
|
Следствия: вероятность того, что случайная величина примет значение, заключённое в интервале 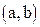 , равна приращению интегральной функции на этом интервале, т.е.
, равна приращению интегральной функции на этом интервале, т.е. 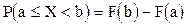 ; вероятность того, что непрерывная случайная величина Х примет одно определённое значение, равна нулю; если возможные значения непрерывной случайной величины расположены на всей оси х, то справедливы следующие предельные соотношения:
; вероятность того, что непрерывная случайная величина Х примет одно определённое значение, равна нулю; если возможные значения непрерывной случайной величины расположены на всей оси х, то справедливы следующие предельные соотношения: 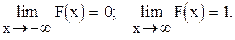
Функцию 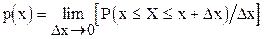
где P 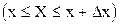 - вероятность попадания случайной величины Х в интервал
- вероятность попадания случайной величины Х в интервал 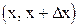 называем плотностью распределения непрерывной случайной величины.
называем плотностью распределения непрерывной случайной величины.
Дифференциальной функцией распределения f(x) (или плотностью вероятности р(х)) является первая производная от интегральной функции, т.е. 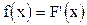 . Следовательно, интегральная функция это первообразная для соответствующей дифференциальной функции.
. Следовательно, интегральная функция это первообразная для соответствующей дифференциальной функции.
Теорема. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (а,b), следующая:
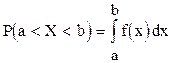
Результат теоремы означает: вероятность того, что непрерывная случайная величина принимает значение, принадлежащее интервалу (a, b), равна площади криволинейной трапеции, ограниченной осью х, кривой распределения f(x) и прямыми x=a и х=b.
Пример. Дана дифференциальная функция случайной величины Х:
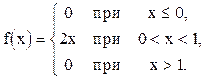
Найти вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу (0,5; 1).
Р е ш е н и е. Искомая вероятность:
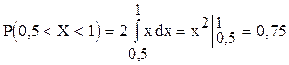 .
.
Дифференциальная функция распределения вероятности непрерывной случайной величины имеет следующие свойства:
1) дифференциальная функция неотрицательна, т.е. f(x)0;
2) несобственный интеграл от дифференциальной функции:
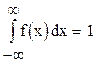 ;
;
3) дифференциальная функция определяет плотность распределения вероятности для каждой точки х.
Из последнего свойства следует: вероятность того, что случайная величина принадлежит интервалу 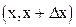 , приближённо равна площади прямоугольника с основанием Dx и высотой f(x).
, приближённо равна площади прямоугольника с основанием Dx и высотой f(x).
Распределением случайных величин называют совокупность значений этих величин, расположенных в возрастающем порядке. Центр распределения характеризуется математическим ожиданием.
Эмпирическим называют распределение относительных частот. Эмпирические распределения изучает математическая статистика.
Теоретическим называют распределение вероятностей. Такие распределения изучает теория вероятностей.
Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [f,b], называют определённый интеграл:
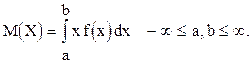 .
.
Математическое ожидание в инженерной практике оценивают средним значением результатов наблюдений.
Дисперсией непрерывной случайной величины называют математическое ожидание квадрата её отклонения, т.е.:
. 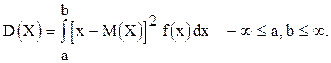
Для среднего квадратичного отклонения имеем:
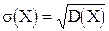 .
.
Симметрия рассеивания случайной величины характеризуется асимметрией. Для дискретных наблюдений:
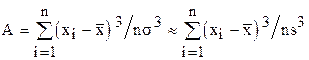
Эксцесс (для дискретных наблюдений):
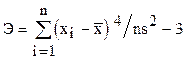 .
.
Асимметрия положительна (А>0), если длинная часть кривой распределения лежит справа от математического ожидания и отрицательная в противном случае. Если эксцесс некоторого распределения отличается от нуля и положительный (Э > 0), то кривая имеет более высокую и острую вершину и наоборот.
Известен ряд законов распределения непрерывных случайных величин: логарифмическое нормальное, полунормальное, гамма-распределение, бета-распределение и др. Центральное место среди законов распределения занимает нормальный закон распределения. Нормальным (распределением Гаусса) является распределение вероятностей случайной величины, которое описывается функцией:
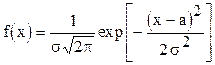
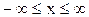 .
.
Для нормального распределения асимметрия и эксцесс равны нулю.
Исследование функции нормального распределения методами математического анализа приводит к следующим результатам: функция определена на всей оси х; при всех значениях х функция принимает положительные значения; ось х служит горизонтальной осью графика функции; при х=а функция имеет максимум, равный 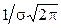 ; график функции симметричен относительно прямой х=а; точки графика
; график функции симметричен относительно прямой х=а; точки графика 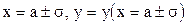 являются точками перегиба.
являются точками перегиба.
Математическое ожидание нормального распределения равно параметру а; среднее квадратичное отклонение этого распределения равно параметру s.
Почему нормально распределённые случайные величины широко распространены на практике? Ответ на вопрос дан математиком А.М. Ляпуновым при доказательстве центральной предельной теоремы теории вероятностей. .Здесь ограничимся следствием из названной теоремы.
Если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждого из которых на всю сумму ничтожно мало, то Х имеет распределение близкое к нормальному.
Пример. Пусть производится измерение некоторого параметра. Любое измерение даёт приближённое значение измеряемой величины, так как на результат оказывают влияние многие независимые случайные факторы (температура, электромагнитные поля, влажность, колебания прибора и др.). Каждый из этих факторов порождает "частную ошибку". Совокупность факторов порождает суммарную ошибку. Рассматривая суммарную ошибку как сумму очень большого числа независимых частных ошибок, можем заключить, что суммарная ошибка имеет нормальное распределение, Это подтверждает опыт.
На практике часто приходится иметь дело с распределением, которое незначительно отличается от нормального (впрочем, отсюда ещё не следует, что нормальное распределение всегда имеет место).
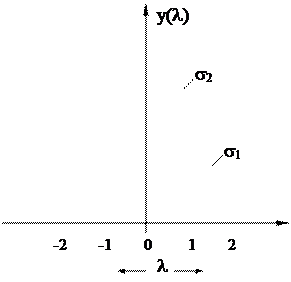
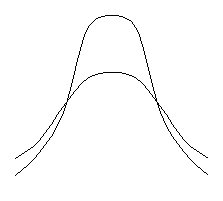
Если изобразить графически нормальные распределения (см. фиг.2.3) с одинаковыми математическими ожиданиями, но с различными средними квадратичными отклонениями, то при меньшем значении s кривая будет падать по обе стороны от вершины более круто, чем при s, имеющей большее значение; с увеличением s кривая становиться более пологой (фиг.2.3,б).
Плотность нормального распределения выражается функцией:
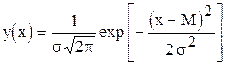 ;
; 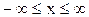 ,
,
где e=2,71828; =3,14159; М и s - математическое ожидание и среднее квадратичное отклонение нормального распределения (являются параметрами распределения).
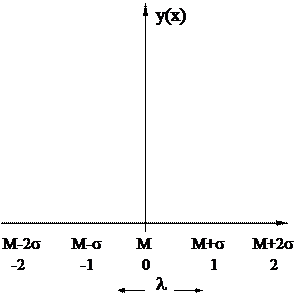 |
а) б)
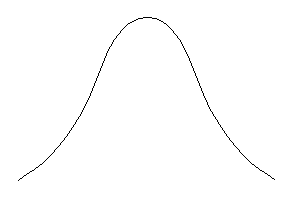
Фиг.2.3. Нормальное распределение (а) и кривые нормального
распределения с различными дисперсиями (б).
Для дальнейшего использования таблиц математической статистики, осуществим замену переменной. Пусть 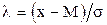 . Тогда
. Тогда
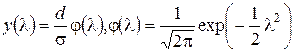 ,
,
где j - плотность нормированного нормального распределения; d - ширина интервала.
Вычисления площади под кривой нормального распределения показывает, что эта площадь всегда равна единице. В связи с этим свойством, площадь, ограниченная ординатами в точках 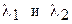 , представляет собой относительную частоту или вероятность попадания значений признака х в интервал
, представляет собой относительную частоту или вероятность попадания значений признака х в интервал 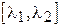 (в интервал
(в интервал 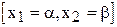 ).
).
Если случайная величина Х задана дифференциальной функцией, то вероятность того, что Х примет значение, принадлежащее 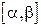 такова:
такова:
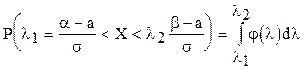 .
.
Пользуясь функцией Лапласа 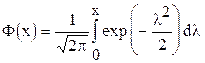 (табл.1, Приложение), имеем:
(табл.1, Приложение), имеем:
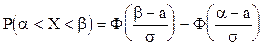 .
.
С помощью введенных формул легко вычислить теоретические значения частот нормального распределения с любым математическим ожиданием и средним квадратичным отклонением.
Пример. Случайная величина Х распределена по нормальному закону. Математическое ожидание и среднее квадратичное отклонение этой величины соответственно равны 30 и 10. Найти вероятность того, что Х примет значение, принадлежащее интервалу (10, 50).
Р е ш е н и е. По условию a=10, b=50, а=30, s=10, следовательно,
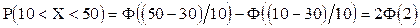 .
.
По табл. значений функции Лапласа находим Ф(х=2)=0,4772. Отсюда искомая вероятность Р(10<X<50)=20,4772=0,9544.
Правило трёх сигм. Между границами находится 99,73% всех наблюдений, т.е. практически все значения. Поэтому принимают следующее утверждение: если какое-либо значение появляется за пределами трёхсигмового участка, то оно является случайным.
На основании правила трёх сигм после вычисления асимметрии и эксцесса можно проверитьподчиняются ли изучаемые наблюдения нормальному закону. Для этого проверяются условия:
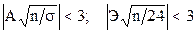 .
.
Если эти условия выполняются, то считают, что наблюдения подчиняются нормальному закону.
Регрессия и корреляция
До сих пор обсуждаемые методы обработки данных касались в основном одного признака. Важной статистической задачей является установление существования взаимосвязи между несколькими факторами (например, необходимо выяснить, изменяются ли два признака самостоятельно, независимо друг от друга, или изменение одного из них вызвано варьированием другого).
Рассмотрим случай, когда у изделия (или процесса) замеряются два признака 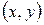 . При этом могут возникать следующие варианты:
. При этом могут возникать следующие варианты:
1. Оба признака 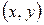 тесно связаны друг с другом (например, длина ребра и объём куба). Этот вид связи называют функциональной. Функциональная связь (или зависимость) между признаками выражается конкретной формулой.
тесно связаны друг с другом (например, длина ребра и объём куба). Этот вид связи называют функциональной. Функциональная связь (или зависимость) между признаками выражается конкретной формулой.
2. Оба признака не строго связаны друг с другом. В этом случае отдельно взятому значению признака  может соответствовать ряд распределения значений
может соответствовать ряд распределения значений 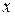 . Если это распределение значений
. Если это распределение значений 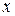 не изменяется с изменением величины
не изменяется с изменением величины  , то оба признака
, то оба признака 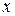 и
и  не зависят друг от друга.
не зависят друг от друга.
3. Если для каждого фиксированного значения  получают распределение признака
получают распределение признака 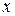 и, наоборот, для каждого фиксированного значения
и, наоборот, для каждого фиксированного значения 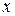 получают распределение признака
получают распределение признака  , то между этими признаками имеется статистическая (корреляционная) связь.
, то между этими признаками имеется статистическая (корреляционная) связь.
При анализе данных, требуется выявить независимые параметры. Для установления корреляционной связи между переменными 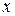 и
и  результаты наблюдений представляют в виде корреляционной матрицы (табл. 2.9). Для этого значения
результаты наблюдений представляют в виде корреляционной матрицы (табл. 2.9). Для этого значения 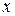 и
и  разбивают на ряд интервалов и определяют средние значения интервалов. В ячейки, образованные пересечением строк и столбцов, заносятся частоты попадания пар значений
разбивают на ряд интервалов и определяют средние значения интервалов. В ячейки, образованные пересечением строк и столбцов, заносятся частоты попадания пар значений 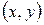 в соответствующие интервалы по
в соответствующие интервалы по 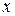 и
и  . В последние строку и столбец записывают суммарные частоты по соответствующим стокам и столбцам.
. В последние строку и столбец записывают суммарные частоты по соответствующим стокам и столбцам.
Уже из обзора табл. 2.9 видно, что с возрастанием 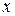 возрастает и
возрастает и  . Однако эту связь нужно выразить количественно и оценить статистически.
. Однако эту связь нужно выразить количественно и оценить статистически.
Эта оценка производится следующим образом.
1. Вычисляем частные средние значения для 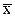 по строкам. Для первой строки значения
по строкам. Для первой строки значения 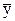 =25 соответствуют значениям
=25 соответствуют значениям 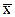 =11 и 13 с частотами 3 и 2. Частная средняя этих значений равна
=11 и 13 с частотами 3 и 2. Частная средняя этих значений равна 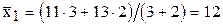 ;
;
для второй строки - 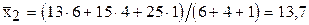 .
.
2. Результаты вычисления частных средних для всех строк запишем в табл.2.10.
3. Отложив данные табл.2.10 на графике, получим корреляционную зависимость  от
от 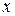 .
.
Связь между двумя количественными признаками проявляется в виде определённой тенденции. Например, если один признак увеличивается, то другой увеличивается или уменьшается. На практике связь между признаками в интересующей экспериментатора области бывает линейной или допускающей линеаризацию (например, логарифмированием, извлечением корня, разложением в ряд и отбрасыванием малых высшего порядка малости).
"Наилучшая" прямая, выравнивающая опытные данные, определяется методом наименьших квадратов, при котором сумма квадратов отклонений  по по вертикали от найденной прямой должна быть минимальной. Эта наилучшая прямая называется линией регрессии у относительно
по по вертикали от найденной прямой должна быть минимальной. Эта наилучшая прямая называется линией регрессии у относительно 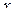 .
.
Таблица 2.9
Корреляционная матрица
| x y | 10-12 11 | 12-14 13 | 14-16 15 | 16-18 17 | 18-20 19 | 20-22 21 | 22-24 23 | 24-26 25 | 26-28 27 | 28-30 29 | 30-32 31 | 32-34 33 | 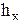
|
| 20-30 25 | 3 | 2 | 5 | ||||||||||
| 30-40 35 | 6 | 4 | 1 | 11 | |||||||||
| 40-50 45 | 1 | 13 | 5 | 19 | |||||||||
| 50-60 55 | 1 | 2 | 4 | 8 | 15 | ||||||||
| 60-70 65 | 1 | 4 | 4 | 2 | 11 | ||||||||
| 70-80 75 | 2 | 6 | 6 | 1 | 15 | ||||||||
| 80-90 85 | 1 | 5 | 6 | ||||||||||
| 90-100 | 1 | 4 | 1 | 6 | |||||||||
| 100-110 | 2 | 4 | 1 | 1 | 8 | ||||||||
| 110-120 | 1 | 1 | 2 | ||||||||||
| 120-130 | 1 | 1 | |||||||||||
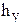
| 3 | 10 | 20 | 9 | 14 | 11 | 9 | 8 | 6 | 6 | 1 | 3 | 100 |
Таблица 2.10
Значения частных средних
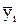
| 25 | 35 | 45 | 55 | 65 | 75 | 85 | 95 | 105 | 115 | 125 |
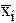
| 12 | 13,7 | 15,4 | 17,5 | 20,1 | 21,8 | 24,7 | 27,0 | 29,3 | 31 | 33 |
Если обозначить через 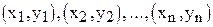 наблюдаемые значения признаков, то линия регрессии выразится в виде
наблюдаемые значения признаков, то линия регрессии выразится в виде 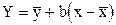 , где
, где 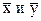 - средние арифметические.
- средние арифметические.
Коэффициент регрессии b определяется по формуле:
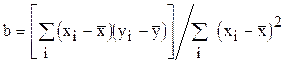 .
.
Если рассматривать характер изменения х по у, т.е. что х зависит от значений признака у, тогда линия регрессии будет иметь вид:
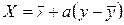 , где
, где 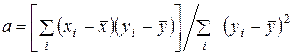 .
.
Заметим, что две линии регрессии, вычисленные по приведенным формулам в случае статистической связи признаков х и у не совпадают.
Тесноту связи между признаками характеризует коэффициент корреляции:
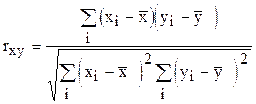 или
или 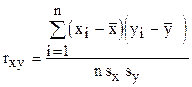 ,
,
где 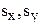 - среднеквадратические отклонения.
- среднеквадратические отклонения.
Чтобы оценить достоверность коэффициента корреляции, необходимо предварительно оценить его ошибку 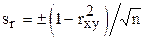 .
.
Далее определяется критерий существенности: 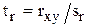 .
.
Если величина 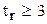 , то коэффициент корреляции считается достоверным, т.е. связь между двумя факторами является доказанной. Если
, то коэффициент корреляции считается достоверным, т.е. связь между двумя факторами является доказанной. Если 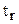 <3, то связь отсутствует.
<3, то связь отсутствует.
Коэффициент корреляции принимает значения в интервале -1, +1. Если 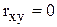 , то линейная связь между признаками х и у отсутствует. Если же, наоборот,
, то линейная связь между признаками х и у отсутствует. Если же, наоборот, 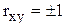 , то между признаками существует линейная функциональная связь. Если r>0, то связь прямая, а если r<0, то связь обратная. В зависимости от величины коэффициента корреляции делают следующие заключения:
, то между признаками существует линейная функциональная связь. Если r>0, то связь прямая, а если r<0, то связь обратная. В зависимости от величины коэффициента корреляции делают следующие заключения:
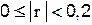
| практически нет связи; |
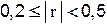
| слабая связь; |
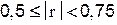
| средняя связь; |
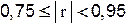
| сильная связь; |
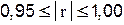
| практически функциональная связь. |
Регрессионный анализ позволяет представить результаты эксперимента в виде функциональной зависимости. В частности, результат эксперимента (функция отклика) может быть описан полиномом:
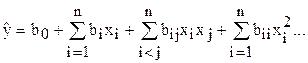 .
.
Введенное уравнение называют уравнением регрессии.
Уравнение регрессии - это приближённая математическая модель процесса или явления, полученная на основе экспериментальных данных. Уравнение адекватно описывает результаты опытов, если среднеквадратичные отклонения экспериментальных данных не превышают ошибку воспроизводимости значений, рассчитанных по уравнению регрессии, т.е. расчётная кривая лежит в поле разброса экспериментальных данных.
Значения коэффициентов регрессии могут быть вычислены методом наименьших квадратов, либо методом ортогональных планов (см. пример в главе 3). После вычисления коэффициентов регрессии осуществляется проверка их значимости. Целью её является выяснение того, с какой степенью достоверности полученные значения коэффициентов регрессии отличаются от нуля.
Для проверки значимости коэффициентов регрессии вычисляется средняя дисперсия воспроизводимости 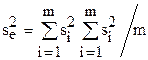 (m - число опытов в одной из серий). Далее вычисляется дисперсия коэффициентов регрессии
(m - число опытов в одной из серий). Далее вычисляется дисперсия коэффициентов регрессии 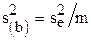 и с использованием t-критерия осуществляется проверка коэффициентов регрессии по формуле
и с использованием t-критерия осуществляется проверка коэффициентов регрессии по формуле 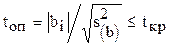 .
.
Если опытное значение t-критерия для какого-либо коэффициента регрессии окажется равным или меньше критического, то данный коэффициент регрессии незначим и влиянием фактора, характеризующегося данным коэффициентом, можно пренебречь.
После оценки значимости коэффициентов регрессии переходим к проверке адекватности (соответствия) выбранного уравнения регрессии опытным данным. Для этого вычисляем дисперсию, характеризующую неадекватность уравнения регрессии:
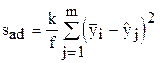
где k - число параллельных измерений; m - число отдельных измерений в одной из серий опытов; f=m-q - число степеней свободы; q - число коэффициентов регрессии; 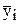 - среднее значение результатов измерений;
- среднее значение результатов измерений; 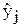 значение результатов измерений, вычисленных по уравнению регрессии (вычисления значений
значение результатов измерений, вычисленных по уравнению регрессии (вычисления значений 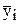 производятся путём подстановки численных значений коэффициентов регрессии в выбранное уравнение регрессии).
производятся путём подстановки численных значений коэффициентов регрессии в выбранное уравнение регрессии).
Определяем опытное значение F-критерия (критерия Фишера):
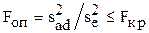 ,
,
где 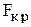 - критическое значение критерия Фишера, определяемое по табл.4 Приложения;
- критическое значение критерия Фишера, определяемое по табл.4 Приложения; 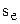 - средняя дисперсия воспроизводимости.
- средняя дисперсия воспроизводимости.
Если опытное значение F-критерия окажется меньше или равно критическому, то принятое уравнение регрессии адекватно описывает экспериментальные данные.
Для применения методов регрессионного анализа необходимо соблюдение следующих условий: значения изучаемых параметров процесса в каждом опыте должны быть независимыми, нормально распределёнными случайными величинами; при этом ошибка в параметрах системы, начальных и граничных условиях должна быть пренебрежимо мала по сравнению с ошибкой в параметрах процесса; дисперсии параметров системы при переходе от опыта к опыту должны быть однородными при достаточной повторяемости опытов.
При обработке эксперимента необходимо наилучшим образом выбрать форму представления его результатов. В качестве такой формы при конструировании математических моделей целесообразно выбирать степенные, экспоненциальные и тригонометрические ряды или их отрезки.
Существенное значение при обработке экспериментальных данных занимает линеаризация эмпирических зависимостей, например, путём логарифмирования экспоненциальных зависимостей. Для некоторой фиксированной и ограниченной области варьирования параметров нелинейные модели (уравнения регрессии) можно привести к линейному виду путём разложения в ряд Тейлора.
Результаты эксперимента могут быть представлены в таблицах, На фотоснимках, на осциллограммах и лентах регистрирующих приборов, в виде записей на магнитные ленты и диски и т.д. Эта информация называется необработанными данными. Обработанные данные составляет та же информация после математической обработки и наглядного (в виде диаграмм, схем, рисунков, графиков и т.д.) представления результатов.
Для дальнейшего изучения предмета рекомендуем использовать руководства по корреляционному и регрессионному анализу, например, монографию Э. Фёрстер, Б. Ренц "Методы корреляционного и регрессионного анализа" M.: Финансы и статистика, 1983. - 302 с.
ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА ДЛЯ ЭКСТРЕМАЛЬНЫХ ЗАДАЧ
При определении оптимальных условий протекания процессов обычно применялся метод поочерёдного варьирования факторов, в частности, метод Гаусса-Зайделя, при котором исследуется окрестность исходной точки, выбирается направление движения к оптимуму и осуществляется малый шаг в этом направлении. Преимуществом метода математического планирования экспериментов является одновременное варьирование всех влияющих факторов и движение к оптимуму кратчайшим путём с минимальным количеством опытов. Начало математическому планированию экспериментов положено в конце 20-х, начале 30-х годах работами Р. Фишера в области дисперсионного анализа и работами Бокса с сотрудниками в 50-х годах. Именно Фишер впервые показал целесообразность одновременного варьирования всеми факторами в противовес широко распространенному однофакторному варьированию. В нашей стране математическое планирование экспериментов получило развитие после выхода в свет в 1965 году книги В.В. Налимова и Н.А. Черновой [9].
Планирование экспериментов имеет большое значение при постановке исследований, направленных на изучение сложных систем и различных многофакторных объектов. Планирование эксперимента повышает его эффективность, даёт наглядную интерпретацию результатов, позволяет уменьшить и оценить случайные и систематические ошибки.
Цели, которые ставятся и решаются при планировании эксперимента во многом совпадают с целями и задачами теории подобия и моделирования. В частности, теория подобия, ставит своей задачей так обобщить опытные данные, чтобы любой эксперимент мог быть закономерно перенесён на неограниченно большой класс явлений, которые признаются подобными данному явлению. Современные тенденции синтеза теории и эксперимента свидетельствуют о целесообразности объединения методов теории подобия и моделирования и планирования эксперимента.
Планирование эксперимента отводит математическим методам активную роль. Здесь статистические методы используются на всех стадиях исследования: при формализации априорной информации перед постановкой опытов; при выборе факторов, влияющих на свойства объекта исследования; при постановке экспериментов и обработке их результатов; при принятии решений.
Как уже отмечалось, основная идея метода планирования - возможность целенаправленного оптимального управления экспериментом при неполном знании механизма изучаемого явления - отвечает идеям кибернетического подхода, предусматривающего формализацию нетворческой части труда исследователя.
При планировании эксперимента существенную роль играют концепции рандомизации и оптимального использования пространства независимых переменных.
Рандомизацией эксперимента называют целенаправленное проведение запланированных опытов в случайной последовательности, с тем чтобы исключить влияние систематических ошибок, вызванных внешними условиями.
В планировании эксперимента используют матрицы планирования, в которых записывают кодированные значения факторов (оба эти понятия будут подробнее рассмотрены).
Если точки в матрице планирования выбраны так, что точность предсказания значений исследуемого параметра одинакова на равных расстояниях от центра факторного пространства и не зависит от направления, то это свойство называется ротатабельностью.
Комбинация факторов, влияющих на проведение эксперимента, называется уровнем факторов. Если число факторов k известно, то можно найти число опытов 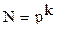 для реализации всех возможных сочетаний уровней факторов (p - число уровней).
для реализации всех возможных сочетаний уровней факторов (p - число уровней).
Если реализуются все возможные сочетания уровней факторов, то эксперимент называется полным факторным. Наряду с ним применяются дробные реплики от полного факторного эксперимента, которыми пользуются для того, чтобы получить линейное приближение небольшого участка поверхности отклика. Целесообразность применения дробных реплик возрастает с ростом числа факторов.
Общая схема планирования экспериментов для решения экстремальных задач состоит из следующих этапов: 1) постановка задачи; 2) выбор параметров оптимизации; 3) выбор факторов; 4) составление линейного плана; 5) реализация линейного плана и построение линейной модели; 6) поиск области экстремума; 7) описание области экстремума; 8) интерпретация результатов.
Выбор параметра оптимизации
Параметр оптимизации – признак, по которому мы хотим оптимизировать процесс. Это может быть зависимая переменная, отклик, выход, целевая функция. Параметр оптимизации должен удовлетворять ряду требований: иметь ясный физический смысл, быть единственным и однозначным в статистическом смысле (является количественным показателем - числом, должен иметь область определения), в экстремальных задачах иметь экстремум. Мы должны уметь его измерять при любой возможной комбинации выбранных уровней факторов.
Статистическая эффективность требует выбора зависимой переменной так, чтобы она определялась с максимальной точностью. Однозначность в статистическом смысле означает, что набору значений независимых переменных должно соответствовать одно с точностью до ошибки эксперимента значение функции отклика.
В технике редко решаются задачи с одной независимой переменной. Параметров оптимизации, как правило, много. Однако, необходимо стремиться к одному параметру оптимизации. Для этого применяют метод априорного ранжирования. Сложную задачу целесообразно свести к последовательности более простых оптимизационных задач. При этом прочие характеристики процесса выступают уже не в качестве параметров оптимизации, а содержат ограничения.
Примерная классификация параметров оптимизации:
- экономические: прибыль, рентабельность, себестоимость, затраты на эксперимент;
- технико-экономические: рентабельность, производительность, надежность, долговечность, КПД;
- технико-технологические: выход продукта, его физические и механические характеристики;
- прочие: психологические, эстетические, статистические (например, уменьшение числа выбросов за пределы допустимого интервала).
Параметр оптимизации должен оценивать действительную эффективность процесса в выбранном смысле – в этом заключается корректность постановки собственно задачи! Параметр оптимизации может изменяться в процессе решения задачи поскольку меняются цели и приоритеты. Он должен давать оценку эффективности системы в целом, а не ее отдельных частей.
ЛИТЕРАТУРА
1. Гмурман В.Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 1972. - 368 с.
2. Веников В.А. Теория подобия и моделирования. М.: Высшая школа, 1976. - 479 с.
3. Адлер Ю.П., Маркова Е.В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий. - М.: Наука, 1976. -279 с.
4. Шенк Х. Теория инженерного эксперимента. - М.: Мир, 1972. - 381 с.;
5. Новик Ф.С., Арсов Я.Б. Оптимизация процессов технологии металлов методами планирования экспериментов. М.: Машиностроение, 1980.
6. Колмогоров В.Л. Механика обработки металлов давлением. М.: 1986. - 688 с.
7. Лель Р.В. Статистическая обработка и планирование экспериментов в технологии машиностроения. Учебное пособие. - Горький: Горьковский гос. университет. 1979. - 67 с.
8. Линник Ю.В. Метод наименьших квадратов и основы математико-статистической теории обработки наблюдений. М.: Физматгиз. 1962.
9. Налимов В.В., Чернова Н.А. Статистические методы планирования экстремальных экспериментов. М.: Наука, 1965.
ПРИЛОЖЕНИЕ
Таблица 1
Таблица значений функции Лапласа Ф(х)
| х | Ф(х) | х | Ф(х) | х | Ф(х) | х | Ф(х) |
| 0,0 | 0,0000 | 1,0 | 0,3413 | 2,0 | 0,4772 | 3,0 | 0,4986 |
| 0,1 | 0,0398 | 1,1 | 0,3643 | 2,1 | 0,4821 | 3,1 | |
| 0,2 | 0,0793 | 1,2 | 0,3849 | 2,2 | 0,4861 | 3,2 | 0,4993 |
| 0,3 | 0,1179 | 1,3 | 0,4032 | 2,3 | 0,4893 | 3,3 | |
| 0,4 | 0,1554 | 1,4 | 0,4192 | 2,4 | 0,4918 | 3,4 | 0,4996 |
| 0,5 | 0,1915 | 1,5 | 0,4332 | 2,5 | 0,4938 | 3,5 | |
| 0,6 | 0,2257 | 1,6 | 0,4452 | 2,6 | 0,4953 | 3,6 | 0,4998 |
| 0,7 | 0,2580 | 1,7 | 0,4554 | 2,7 | 0,4965 | 3,7 | |
| 0,8 | 0,2881 | 1,8 | 0,4641 | 2,8 | 0,4974 | 3,8 | 0,4999 |
| 0,9 | 0,3159 | 1,9 | 0,4713 | 2,9 | 0,4971 | 5,0 | 0,4999 |
Таблица 2
Критические точки распределения Пирсона 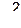
| Число степе- | Уровень значимости | ||||||
| ней свободы | 0,99 | 0,98 | 0,95 | 0,90 | 0,05 | 0,025 | 0,01 |
| 1 | 0,00016 | 0,0006 | 0,0039 | 0,016 | 0,039 | 0,001 | 0,000 |
| 2 | 0,020 | 0,040 | 0,103 | 0,211 | 0,103 | 0,051 | 0,020 |
| 3 | 0,115 | 0,185 | 0,352 | 0,584 | 0,352 | 0,216 | 0,115 |
| 4 | 0,297 | 0,43 | 0,71 | 1,06 | 0,711 | 0,484 | 0,297 |
| 5 | 0,554 | 0,75 | 1,14 | 1,61 | 1,15 | 0,831 | 0,554 |
| 6 | 0,872 | 1,13 | 1,63 | 2,20 | 1,64 | 1,24 | 0,872 |
| 7 | 1,24 | 1,56 | 2,17 | 2,83 | 2,17 | 1,69 | 1,24 |
| 8 | 1,65 | 2,03 | 2,73 | 3,49 | 2,73 | 2,18 | 1,65 |
| 9 | 2,09 | 2,53 | 3,32 | 4,17 | 3,33 | 2,70 | 2,09 |
| 10 | 2,56 | 3,06 | 3,94 | 4,86 | 3,94 | 3,25 | 2,56 |
| 11 | 3,05 | 3,6 | 4,6 | 5,6 | 4,57 | 3,82 | 3,05 |
| 12 | 3,57 | 4,2 | 5,2 | 6,3 | 5,23 | 4,40 | 3,57 |
Таблица 3
Значения критерия Кохрена для уровня значимости 0,05
| f m | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 2 | 0,9985 | 0,9750 | 0,9392 | 0,9057 | 0,8772 | 0,8534 | 0,8332 | 0,8159 |
| 3 | 0,9689 | 0,8709 | 0,7977 | 0,7457 | 0,7071 | 0,6771 | 0,6530 | 0,6333 |
| 4 | 0,9065 | 0,7679 | 0,6841 | 0,6287 | 0,5895 | 0,5598 | 0,5365 | 0,5175 |
| 5 | 0,8412 | 0,6838 | 0,5981 | 0,5441 | 0,5665 | 0,4783 | 0,4564 | 0,4387 |
| 6 | 0,7808 | 0,6161 | 0,5321 | 0,4803 | 0,4447 | 0,4184 | 0,3980 | 0,3817 |
| 7 | 0,7271 | 0,5612 | 0,4800 | 0,4307 | 0,3974 | 0,3725 | 0,3535 | 0,3384 |
| 8 | 0,6798 | 0,5157 | 0,4377 | 0,3910 | 0,3595 | 0,3362 | 0,3185 | 0,3043 |
| 9 | 0,6385 | 0,4775 | 0,4027 | 0,3584 | 0,3286 | 0,3067 | 0,2901 | 0,2768 |
| 10 | 0,6020 | 0,4450 | 0,3733 | 0,3311 | 0,3029 | 0,2823 | 0,2666 | 0,2541 |
Таблица 4
Значения F-критерия для уровня значимости 0,05
( 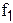 - число степеней свободы большей дисперсии,
- число степеней свободы большей дисперсии, 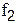 - число степеней свободы меньшей дисперсии)
- число степеней свободы меньшей дисперсии)
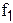
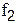
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 161 | 200 | 216 | 225 | 230 | 234 | 237 | 239 | 241 | 242 |
| 2 | 18,51 | 19,00 | 19,16 | 19,25 | 19,30 | 19,33 | 19,36 | 19,37 | 19,38 | 19,39 |
| 3 | 10,13 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,88 | 8,84 | 8,81 | 8,78 |
| 4 | 7,71 | 6,34 | 6,59 | 6,39 | 6,26 | 6,16 | 6,09 | 6,04 | 6,00 | 5,96 |
| 5 | 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,96 | 4,88 | 4,82 | 4,78 | 4,74 |
| 6 | 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,21 | 4,15 | 4,10 | 4,06 |
| 8 | 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | 3,50 | 3,44 | 3,39 | 3,34 |
| 10 | 4,96 | 4,10 | 3,71 | 3,48 | 3,33 | 3,22 | 3,14 | 3,07 | 3,02 | 2,97 |
| 12 | 4,75 | 3,86 | 3,49 | 3,26 | 3,11 | 3,00 | 2,92 | 2,85 | 2,80 | 2,76 |
| 14 | 4,60 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 | 2,77 | 2,70 | 2,65 | 2,60 |
| 3,84 | 2,99 | 2,60 | 2,37 | 2,21 | 2,09 | 2,01 | 1,94 | 1,88 | 1,83 |
Таблица 5
Значение t-критерия для различных уровней значимости
| Число | Уровни значимости | ||||
| степеней свободы | 0,10 | 0,05 | 0,02 | 0,01 | 0,001 |
| 1 | 6,31 | 12,71 | 31,82 | 63,66 | 63,62 |
| 2 | 2,92 | 4,30 | 6,97 | 9,93 | 31,60 |
| 3 | 2,35 | 3,18 | 4,54 | 5,84 | 12,94 |
| 4 | 2,13 | 2,78 | 3,75 | 4,60 | 8,61 |
| 5 | 2,02 | 2,57 | 3,37 | 4,08 | 6,85 |
| 6 | 1,94 | 2,45 | 3,14 | 3,71 | 5,96 |
| 7 | 1,90 | 2,37 | 3,00 | 3,50 | 5,41 |
| 8 | 1,86 | 2,31 | 2,90 | 3,36 | 5,04 |
| 9 | 1,83 | 2,26 | 2,82 | 3,25 | 4,78 |
| 10 | 1,81 | 2,23 | 2,76 | 3,17 | 4,59 |
| 11 | 1,80 | 2,20 | 2,72 | 3,11 | 4,44 |
| 12 | 1,78 | 2,18 | 2,68 | 3,06 | 4,32 |
| 13 | 1,77 | 2,16 | 2,65 | 3,01 | 4,22 |
| 14 | 1,76 | 2,15 | 2,62 | 2,98 | 4,14 |
| 15 | 1,75 | 2,13 | 2,60 | 2,95 | 4,07 |
| 16 | 1,75 | 2,12 | 2,58 | 2,92 | 4,02 |
| 17 | 1,74 | 2,11 | 2,57 | 2,90 | 3,97 |
Таблица 6
Критерии подобия механических и тепловых явлений
| 1. Критерий гомохронности, характеризующий однородность процессов во времени: t - время; v -скорость; l - расстояние | 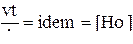
|
| 2. Критерий Ньютона: F - сила; M - масса | 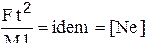
|
| 3. Критерий Фруда: g - ускорение свободного падения | 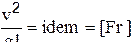
|
| 4. Критерий Эйлера - плотность | 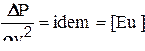
|
5. Критерий Рейнольдса, характеризующий процессы в несжимаемой жидкости:
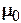 - вязкость - вязкость
| 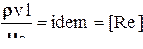
|
6. Критерий Архимеда, характеризующий процесс движения жидкости при различной её плотности:
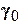 - коэффициент кинематической вязкости - коэффициент кинематической вязкости
| 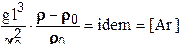
|
| 7. Критерий Жуковского | 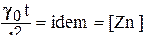
|
8. Критерий Фурье: 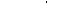 - коэффициент температуропроводности; - коэффициент температуропроводности;  - коэффициент теплоёмкости; - удельный вес - коэффициент теплоёмкости; - удельный вес
| 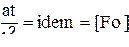
|
| 9. Критерий Пекле для движущейся жидкости с заданным тепловым состоянием | 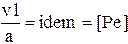
|
| 10. Критерий Нуссельта: - коэффициент теплоотдачи | 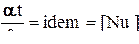
|
| 11. Критерий Кирпичёва: k - коэффициент теплопередачи | 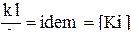
|
| 12. Критерий Прандтля | 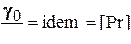
|
13. Критерий Био:
 - постоянная Стефана Больцмана;
- температура - постоянная Стефана Больцмана;
- температура
| 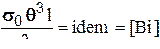
|
РОССИЙСКАЯ АКАДЕМИЯ НАУК - УРАЛЬСКОЕ ОТДЕЛЕНИЕ
ИНСТИТУТ МАШИНОВЕДЕНИЯ УрО РАН
Дата: 2019-05-29, просмотров: 376.