Прежде всего необходимо дать определение фактора. Фактором будем называть измеряемую переменную величину, в некоторый момент времени принимающую определенное значение. Также как и параметр оптимизации каждый фактор имеет область определения, т.е. совокупность всех значений, которые в принципе может принимать данный фактор. Факторы могут быть количественными и качественными, хотя, в принципе, качественным факторам можно дать количественную оценку по определенной шкале.

При выборе факторов необходимо ограничивать область их возможного варьирования. Для каждого фактора устанавливается основной уровень и интервалы варьирования.

Как выбирать факторы? Если при постановке задачи пропустить сильно влияющий фактор, то экспериментальная работа может оказаться не эффективной. Поэтому при планировании эксперимента в его план включают все влияющие, по мнению исследователя, факторы. При их большом числе возникает задача отсеивания незначимых факторов. Вспомним, что необходимое число опытов определяемое по формуле 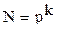 с увеличением числа факторов растет по показательной функции. Возникает ситуация, известная под названием «проклятие размерности».

Для того, чтобы избежать данной ситуации, необходимо ограничить число факторов. Один из способов решения указанной задачи - проведение априорного ранжирования факторов. Такого типа эксперимент проводится путём обработки данных, полученных при опросе специалистов, или на основе данных литературы. Цель эксперимента заключается в сравнительной оценке влияния различных факторов на параметры оптимизации. В результате проводится обоснованный отбор факторов для последующего экспериментального исследования и исключение факторов, влияние которых несущественно.

       Априорное ранжирование факторов основано на том, что факторы, оказывающие согласно априорной информации влияние на параметры оптимизации, ранжируются в порядке убывания относительного вклада. Вклад фактора оценивается по величине ранга (места), которое отведено при опросе исследователем данному фактору в степени влияния на параметр оптимизации. Процедура априорного ранжирования заключается в следующем. Каждому специалисту при опросе предлагается заполнить анкету, в которой указаны факторы, их размерность и предполагаемые интервалы варьирования. Необходимо назначить место каждому фактору, включить новые факторы или высказать мнение об изменении интервала варьирования.

       В качестве примера в табл. 3.1. показаны результаты опроса 4-х специалистов.

       Таблица 3.1

Матрица результатов опроса специалистов

Специалисты	Факторы
j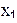
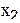
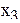
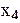
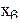
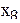
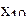
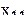
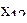
j=1	8	10,5	10,5	10,5	1	2,5	2,5	10,5	5	4	7	6
2	8	9	10	11	1	6,5	6,5	12	2	3	4	5
3	6	7,5	7,5	11	2	4,5	4,5	12	1	3	9,5	9,5
4=m	7	4	8	10,5	2	10,5	10,5	10,5	1	3	5,5	5,5
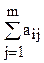
	29	31	36	43	6	24	24	45	9	13	26	26
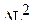
	9	25	100	289	400	4	4	361	289	169	0	0

       При планировании эксперимента факторы должны удовлетворять определенным требованиям. Факторы должны быть управляемыми, например, если есть возможность выбрав значение фактора, поддерживать его постоянным в течение эксперимента. Необходимо указать последовательность действий, с помощью которых устанавливаются определенные значения (уровни) фактора, т.е. фактор должен быть операциональным. С указанным понятием связаны также выбор размерности фактора и точность его фиксирования. Степень точности измерения должна быть высокой и зависит в свою очередь от диапазона изменения фактора.

Рассмотрим кодирование факторов. Исследуем влияние двух факторов 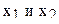 на результат эксперимента у. Фактор  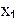принимает значения 10 и 40, а фактор  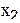значения 1 и 5. Так как факторы варьируются на двух уровнях, имеется лишь четыре комбинации факторов, соответствующие вершинам прямоугольника на плоскости  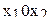(фиг. 3.1).

       Перенесём начало координат в центр исследуемой области ( в центр прямоугольника). Числовые значения влияющих факторов, через которые проходят после переноса оси координат, называются основными уровнями факторов 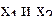. В данном примере

.

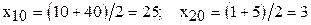Крайние, относительно основного уровня, значения факторов называются верхним и нижним уровнями варьирования факторов. Верхний уровень (обозначение «+»)- это значение фактора, откладываемое в положительном направлении оси координат. Нижний уровень - это значение фактора, откладываемого в отрицательном направлении оси координат (обозначение «-»). Обычно для упрощения записи условий эксперимента и обработки данных масштабы по осям выбираются так, чтобы верхний уровень соответствовал +1, нижний уровень значению –1, а основной – нулю. 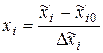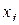Для факторов, имеющих непрерывную область определения это легко сделать с помощью формулы: , где  -кодированное значение фактора,  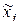- натуральные значения,  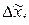- интервал варьирования.

       Наряду с уровнями факторов вводятся единицы варьирования l₁, l₂. Для рассматриваемого случая l₁=40-25=15, l₂=5-3=2.

Выбор единиц варьирования определяются условиями протекания конкретных процессов, подлежащих исследованию и оптимизации. Выбор основного уровня факторов соответствует выбору некоторой точки на поверхности отклика, исходной для движения к экстремуму. Рассмотрим его несколько подробнее. Наилучшим условиям, определенным из анализа априорной информации, соответствует некоторая комбинация уровней факторов, которую можно рассматривать как многомерную точку в факторном пространстве. Построение плана эксперимента сводится к выбору экспериментальных точек, симметричных относительно нулевого уровня.

Сведения о наилучших условиях обычно являются неполными. Если есть сведения о наилучшей точке но границы неизвестны, остается рассматривать эту точку в качестве основного уровня. Аналогично – если известны границы и наилучшие условия лежат внутри области. Если наилучшая точка лежит близко к границе – основной уровень задается с некоторым сдвигом от нее. Наконец, если имеем несколько эквивалентных точек внутри области, выбор между ними определяется дополнительными соображениями.

Условия проведения опытов представляют в таблицах.

Таблица 3.2.

Пример таблицы для условий проведения опытов

	Факторы
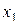
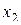
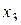
Основной уровень (0)	0,40	840	60
Интервал варьирования ( 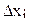)	0,15	100	60
Верхний уровень (+1)	0,55	940	120
Нижний уровень (-1)	0,25	740	0

Кодированная система координат позволяет компактно и наглядно записать порядок проведения экспериментов в виде матрицы (плана) экспериментов. Различают планы первого и второго порядка. В планах первого порядка влияющие факторы варьируются на двух уровнях, в планах второго порядка - на трёх уровнях. Планы первого порядка обозначаются  (k - число факторов).

3.3. Составление линейного плана

       Ответственным этапом планирования эксперимента является составление линейного плана, реализация опытов которого преследует цель отыскания пока ещё не оптимума, а лишь направления к нему. Допустим, что в задаче варьируются только два фактора, причём каждый на двух уровнях +1 и -1 (см. табл. 3.1). Все возможные комбинации факторов будут исчерпаны в четырёх опытах (табл. 3.2). Здесь имеем линейный план для линейной модели. Этот план характеризуется варьированием факторов на двух уровнях. Если число факторов и число уровней равно двум, то реализуется полный факторный эксперимент типа 2².

       Табл. 3.3 называется матрицей планирования полного факторного эксперимента типа 2². Во втором столбце приведены значения фиктивной переменной 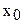=+1 (её оценка даёт величину свободного члена в уравнении регрессии); в пятом столбце учитываются парные взаимодействия. По результатам четырёх опытов (шестой столбец) можно вычислить четыре коэффициента уравнения регрессии: 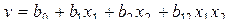. Последнее слагаемое в формуле характеризует эффект взаимодействия – в случае, если эффект одного фактора зависит от уровня, на котором находится другой фактор.

Коэффициенты 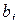 вычисляются по следующей формуле:

.

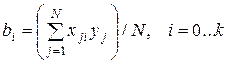Таблица 3.3.

Матрица планирования полного факторного эксперимента типа 2²

№ опыта	Факторы				Отклик
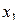
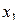
1	+	+	+	+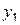
2	+	-	+	-
3	+	+	-	-
4	+	-	-	+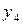

       Техника полного факторного эксперимента с варьированием факторов на двух уровнях сводится к реализации 2^k опытов, где k - число факторов. Для построения матрицы полного факторного эксперимента при любом k дважды повторяется матрица планирования для случая k-1 (сначала при значении k-го фактора на верхнем уровне, а затем на нижнем). Последовательное достраивание матриц при увеличении k от 2 до 4-х показано в таблице 3.4. Первые четыре (отчёркнутые) опыта представляют собой матрицу типа 2²; отчёркнутые восемь опытов представляют собой матрицу планирования 2³ шестнадцать опытов представляют собой матрицу планирования 2⁴.

Для построения матрицы трёхфакторного эксперимента 2³ дважды переписываем матрицу 2². Полученную матрицу дополняем так, как это показано в табл. 3.4.

       В полном факторном эксперименте увеличение числа факторов быстро увеличивает число опытов. Так, при трёх факторах необходимо провести 2³=8 опытов, при пяти факторах 2⁵=32, при восьми - 2⁸=256 опытов. В то же время, изначально ничего не известно об области оптимума. Возникает необходимость с минимальными затратами предварительно изучить поверхность отклика. Для этого используют линейные уравнения и дробные реплики.

Таблица 3.4

Матрица трёхфакторного эксперимента

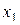
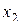
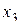
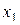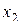
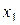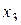
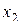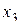
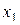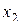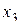
№ опытов									у
1	+	+	+	+	+	+	+	+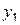
2	+	-	+	+	-	-	+	-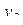
3	+	+	-	+	-	+	-	-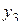
4	+	-	-	+	+	-	-	+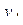
5	+	+	+	-	+	-	-	-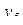
6	+	-	+	-	-	+	-	+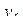
7	+	+	-	-	-	-	+	+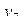
8	+	-	-	-	+	+	+	-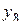

Таблица 3.5

Матрицы полных факторных экспериментов типов: 2², 2³, 2⁴

Опыт №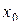
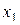
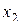
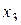
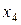
1	+	+	+	+	+
2	+	-	+	+	+
3	+	+	-	+	+
4________	+________	-________	-_______	+	+
5	+	+	+	-	+
6	+	-	+	-	+
7	+	+	-	-	+
8________	+________	-________	-________	-_______	+
9	+	+	+	+	-
10	+	-	+	+	-
11	+	+	-	+	-
12	+	-	-	+	-
13	+	+	+	-	-
14	+	-	+	-	-
15	+	+	-	-	-
16	+	-	-	-	-

Пример. Предположим, что изучается влияние трёх факторов. Полный факторный эксперимент должен включать 8 опытов. Для того, чтобы на первом этапе исследования ограничиться 4-мя опытами, в матрице, представленной табл. 3.3, парное взаимодействие факторов заменяем действием третьего фактора. В результате имеем матрицу (табл. 3.6).

Таблица 3.6.

Матрица планирования факторного эксперимента типа 2^3-1

№ опыта	Фактор				Отклик
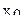
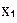
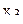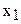
				=	y
1	+	+	+	+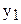
2	+	-	+	-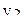
3	+	+	-	-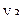
4	+	-	-	+

       Планирование считается оптимальным, если оно связано с проведением несложных вычислений и позволяет получать независимые оценки коэффициентов регрессии, определяемые с одинаковой дисперсией. Важно также, чтобы дисперсии параметров оптимизации, предсказываемого уравнения регрессии, не зависели от вращения системы координат в центре плана. Перечисленным условиям отвечает планирование, обладающее свойствами ортогональности и ротатабельности. При полном факторном эксперименте матрица планирования должна иметь следующие свойства:

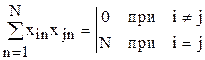и .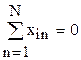

Здесь i,j=0,1,2,...K; K - число факторов, N - число опытов в матрице планирования, n - номер опыта. Первая из формул показывает свойства ортогональности и нормировки. Вторая формула – симметрия относительно центра эксперимента. Свойства симметрии и нормировки следуют непосредственно из способа построения матрицы.

       Приведенные условия свидетельствуют о том, что планирование в данном случае ортогонально (это облегчает вычислительную работу), все факторы расположены симметрично относительно центра факторного пространства и коэффициенты регрессии оцениваются с минимальной дисперсией. Кроме того, такое планирование является также и ротатабельным, в результате чего информация, содержащаяся в уравнении регрессии, равномерно распределена по гипосфере относительно центра эксперимента, а предсказанные значения параметра оптимизации имеют минимальные дисперсии в различных точках факторного пространства, причём на равных расстояниях от центра эксперимента эти дисперсии равны.

       В табл.3.7 приведен пример ротатабельного плана. Напомним, что планирование называется ротатабельным, если обеспечивается требование инвариантности плана при вращении системы координат относительно центра. Параллельные опыты в центре плана позволяют рассчитать оценку дисперсии ошибок наблюдений.

Таблица 3.7

Ротатабельный план трёхфакторного эксперимента

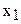
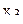
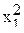
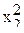
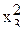
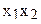
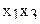
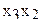
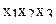
№ оп.											y
1	+	+	+	+	+	+	+	+	+	+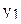
2	-	+	+	+	+	+	-	-	+	-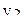
3	+	-	+	+	+	+	-	+	-	-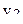
4	-	-	+	+	+	+	+	-	-	+
5	+	+	-	+	+	+	+	-	-	-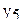
6	-	+	-	+	+	+	-	+	-	+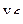
7	+	-	-	+	+	+	-	-	+	+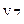
8	-	-	-	+	+	+	+	+	-	-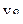
9	+1,682	0	0	2,828	0	0	0	0	0	0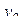
10	-1,682	0	0	2,828	0	0	0	0	0	0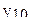
11	0	+1,682	0	0	2,828	0	0	0	0	0
12	0	-1,682	0	0	2,828	0	0	0	0	0
13	0	0	+1,682	0	0	2,828	0	0	0	0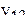
14	0	0	-1,682	0	0	2,828	0	0	0	0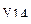
15	0	0	0	0	0	0	0	0	0	0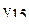
16	0	0	0	0	0	0	0	0	0	0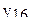
17	0	0	0	0	0	0	0	0	0	0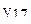
18	0	0	0	0	0	0	0	0	0	0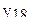
19	0	0	0	0	0	0	0	0	0	0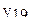
20	0	0	0	0	0	0	0	0	0	0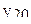

Что такое дробные реплики? Допустим, мы имеем дело с линейной моделью 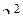. Нам необходимо определить коэффициенты  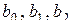и для этого имеем 4 уравнения. Лишнее уравнение описывало у нас эффект взаимодействия (см. табл. 3.3). Используем эту лишнюю степень свободы для минимизации числа опытов. В данном случае столбец  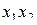используем для нового фактора .

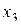Таблица 3…

Номер опыта
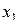
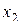
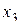
1	+	+	+	+
2	-	-	+	+
3	+	-	-	+
4	-	+	-	+

Символическое обозначение произведения столбцов матрицы (последний столбец табл. 3…) называется определяющим контрастом и записывается в виде: 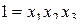 (если был выбран способ подстановки 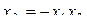, мы получили бы вторую половину матрицы или полуреплику с определяющим контрастом 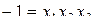). Контраст помогает определять смешанные эффекты. Для того, чтобы определить, какой эффект смешан с данным, надо обе части определяющего контраста умножить на столбец, соответствующий нужному эффекту, например: , т.к. всегда 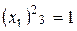 и значит имеем смешанную оценку коэффициентов (мы не можем их различить) вида :  и аналогично 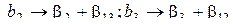. Но, поскольку мы постулируем линейную модель, все парные взаимодействия для нас незначимы. Соотношение, показывающее с каким из эффектов смешан данный эффект, называется генерирующим соотношением.

       Поставив четыре опыта для оценки влияния трех факторов мы воспользовались половиной полного факторного эксперимента 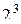 или полурепликой, которая обозначается 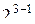. При использовании обеих полуреплик можно получить раздельные оценки линейных эффектов и эффектов взаимодействия, как в полном факторном эксперименте. В случае матрицы  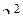у практически нас не было выбора, к чему приравнять 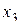. С увеличением числа факторов увеличиваются и возможности, причем количество факторов, образующих взаимодействие – различно.

Введем понятие разрешающей способности полуреплики. Величина ее равна максимальному числу факторов в определяющем контрасте. Разрешающая способность будет максимальной если линейные эффекты смешаны с эффектами наибольшего возможного порядка. В этом случае реплики имеют максимальную разрешающую способность и называются главными. Например, выше мы рассмотрели главную полуреплику, которая обозначается следующим образом: 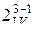. При отсутствии дополнительной информации выбирают реплики с максимальной разрешающей способностью, поскольку тройные эффекты менее существенны чем двойные и т.д. В общем случае дробные реплики получают делением числа опытов соответствующего полного факторного эксперимента на число равное 2. Так получают реплики:  и т.д. В общем случае эти реплики связаны с планированием типа 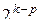, где р - число линейных членов, приравненных эффектам взаимодействий.

Рассмотрим в общих чертах процедуру выбора 1/4 – реплик. Допустим, мы имеем пять факторов. Тогда вместо 32 опытов можно использовать только 8, если воспользоваться

репликой 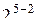. Допустим, мы приравняем  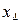парному взаимодействию, а  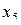- тройному.

Тогда будут возможны 12 вариантов взаимодействий:

;                   ;

;                ;

;                   ;

;                ;

;                  ;

;               .

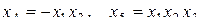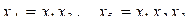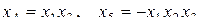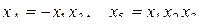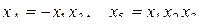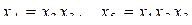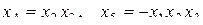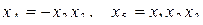       Допустим, выбран пятый вариант: 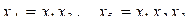. Тогда определяющими контрастами будут являться:  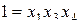и 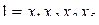. Перемножив эти соотношения можем получить третье соотношение: 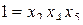. Здесь мы введем также понятие обобщающего определяющего контраста: .

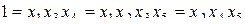       Система смешивания будет получаться умножением обобщающего определяющего контраста последовательно на 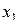,  и т.д. В результате получим:

;      ;

;      ;

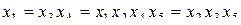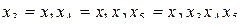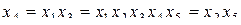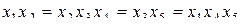…    и т.д.

       При этом получается довольно сложная система смешивания линейных эффектов с эффектами второго, третьего и четвертого порядков, например:

, … …

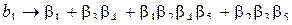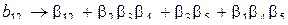       Допустим, коэффициент 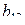 или аналогичный отличен от нуля. Можно ли в этом случае пренебрегать парными взаимодействиями? Если нет, то следует поставить вторую серию опытов, выбрав другую 1/4 – реплику, например, методом “перевала”. При этом вторая четверть-реплика получается из первой путем изменения всех знаков в матрице на обратные. Тогда в обобщающем определяющем контрасте тройные произведения поменяют знак. Поскольку тройные произведения определяют парные эффекты взаимодействия в совместных оценках для линейных эффектов, то усреднив результаты по обеим четверть-репликам можно получить линейные эффекты, не смешанные с парными.