Обработка данных — процесс подготовки, группировки данных, расчета и анализа показателей с использованием методов математической статистики. Компьютерная обработка данных предполагает математическое преобразование данных с помощью определенных программных средств. Для этого необходимо иметь представление как о математических методах обработки данных, так и о соответствующих программных средствах

Этапы обработки информции:

-Подготовка данных

-Группировка данных

-Расчет статистических показателей

-Статистический анализ данных

-Логический анализ и интерпритация полученных результатов

Подготовка данных включает в себя передачу данных в специальную компьютерную программу для предварительной их обработки, визуализации и формирования целостного представления о структуре и качестве исследуемого материала.

Под группировкой данных понимают распределение статистической совокупности на однородные группы по одному (простая группировка) или нескольким (комбинированная группировка) признакам. Группировка может быть первичной, когда ряды строят непосредственно из единиц наблюдения, и вторичной, когда производят укрупнение групп на основе ранее сгруппированного материала.

В медико-социальных исследованиях используют самые разнообразные группировки: по социально-демографическим (пол, возраст, брачное состояние, национальный состав); климато-географическим (сезон года, место жительства и др.); социально-экономическим признакам (профессия, образование, доход и др.); характеристикам здоровья (заболевания, причины инвалидности, смертности и др.); типам учреждений (поликлиника, больница и др.)

Расчет статистических показателей.

Статистический показатель — одна из многих количественных характеристик совокупности, численное выражение внутренней сущности изучаемого явления.

В зависимости от охвата единиц совокупности показатели подразделяются на индивидуальные, характеризующие отдельный объект, и сводные, характеризующие группу объектов. Также статистические показатели можно классифицировать на абсолютные, относительные, средние, интегральные.

Абсолютные статистические показатели характеризуются определенной размерностью и единицами измерения. Примерами абсолютных показателей являются данные о численности населения, числе работающих врачей, функционирующих больничных или амбулаторно-поликлинических учреждений (АПУ) и др. Основным недостатком абсолютных величин является то, что сравнение их друг с другом может привести к ошибочным выводам.

Относительные статистические показатели более объективно выражают количественные соотношения между явлениями. Для анализа здоровья населения и деятельности системы здравоохранения выделяют следующие группы относительных показателей:

- экстенсивные показатели;

- интенсивные показатели;

- показатели соотношения;

- показатели наглядности.

Экстенсивные показатели (показатели распределения) отражают внутреннюю структуру явления, распределение его на составные части, удельный вес каждой части в целом и выражаются в процентах. Эти показатели дают возможность сопоставлять структуры одной и той же совокупности в различные моменты времени, делать выводы о тенденциях и закономерностях структурных изменений в динамике. К экстенсивным показателям относятся структура заболеваемости, инвалидности, смертности, коечного фонда, врачебных специальностей и др.

Характерной чертой экстенсивных показателей является их взаимосвязанность, вызывающая известный автоматизм сдвигов, так как их сумма всегда составляет 100%.

Интенсивные показатели (показатели частоты, распространенности) характеризуют уровень, распространенность какого-либо явления в среде, которое непосредственно связано с этой средой. Эти показатели рассчитывают, как правило, для анализа здоровья населения, где в качестве среды берут численность населения, а в качестве явления — число рождений, заболеваний, смертей и др. и выражают в процентах (%), промилле (%о), децимилле (%оо) сантимилле (%ооо). К интенсивным показателям относятся показатели заболеваемости, рождаемости, смертности населения и др.

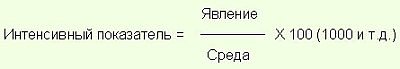
Интенсивные показатели могут быть общими и специальными. Общие показатели характеризуют явление в целом, например общие коэффициенты рождаемости, смертности, заболеваемости, вычисленные по отношению ко всему населению РФ, города, района и др. Для более углубленного и дифференцированного анализа явлений необходимо пользоваться специальными интенсивными показателями, особенностью которых является уточнение группировки. Например, при вычислении специальных коэффициентов рождаемости (плодовитости) за среду берется не все население, а только женщины в возрасте 15-49 лет.

Показатели соотношения характеризуют уровень (распространенность) какого-либо явления в среде, непосредственно (биологически) не связанного с этой средой. Показатели соотношения рассчитывают, как правило, для анализа деятельности системы здравоохранения, ее ресурсного обеспечения, где в качестве среды берут численность населения, а в качестве явления — число врачей, средних медицинских работников, больничных коек, посещений АПУ и др. и выражают в процентах, промилле, децимилле, сантимилле. К показателям соотношения относятся обеспеченность населения стационарной, амбулаторно-поликлинической помощью, врачами, средними медицинскими работниками и др.

                                                       явление х 100 (1000, 10000, 100000)

показатель соотношения = ---------------------------------------------------------

                                                       среда, не являющаяся основанием

                                                       для возникновения данного явления

Показатели наглядности применяют для анализа степени изменения изучаемого явления во времени. Они указывают, на сколько процентов или во сколько раз произошло увеличение или уменьшение сравниваемых показателей за данный период времени. Показатели наглядности получают при отношении ряда сравниваемых величин к исходной величине, принятой за 100 или за 1.

                                                       значение величины в данный момент времени

Показатель наглядности = ----------------------------------------------------------------------------

                                                       значение величины в начальный момент времени

Средние величины. Характеризуют весь ряд наблюдений одним числом. Средняя величина нивелирует, ослабляет случайные отклонения индивидуальных наблюдений в ту или иную сторону и характеризует основное, типичное свойство явления.

В практической деятельности врача средние величины используют, например, для характеристики физического здоровья населения (рост, масса тела, окружность груди, данные спирометрии, динамометрии, становая сила и др.). Использование их в виде региональных стандартов имеют большое практическое значение для анализа здоровья населения, в особенности детей, спортсменов, военнослужащих, а также лиц, находящихся на диспансерном учете. Кроме того, средние величины широко используют для анализа деятельности организаций здравоохранения.

Для расчета средних величин необходимо соблюдать следующие условия:

— средние величины должны быть рассчитаны на основе качественно однородных статистических групп;

- средние величины исчисляют на совокупностях, имеющих достаточно большое число наблюдений.

В медико-социальных исследованиях используют следующие виды средних величин: среднее арифметическое, среднее арифметическое взвешенное, среднее гармоническое взвешенное, среднее геометрическое невзвешенное, среднее геометрическое взвешенное, среднее квадратическое невзвешенное, среднее квадратическое взвешенное.

К средним величинам относят также моду как наиболее типичное значение и медиану как середину распределения случайной величины.

Интегральные показатели (ИП) разрабатываются для комплексной оценки состояния здоровья населения и его прогнозирования. Интегральный показатель (ИП) — результирующий показатель, учитывающий совокупное влияние отдельных как независимых, так и взаимосвязанных факторов.

ИП разрабатываются на основе построения математических моделей, которые подразделяются на линейные и нелинейные, могут быть однопараметрическими и многопараметрическими.

ИП используют для проведения сравнительного анализа здоровья населения отдельных административных территорий (муниципальных районов, субъектов РФ, федеральных округов), а также построения прогнозов. Кроме того, ИП могут быть использованы для анализа причинно-следственных связей показателей здоровья населения и загрязнения среды обитания, для оценки деятельности системы здравоохранения, а также определения социального и экономического ущерба вследствие заболеваемости, инвалидизации и преждевременной смертности населения.

Стандартизованные коэффициенты.

Существуют прямой, косвенный и обратный методы вычисления стандартизованных коэффициентов.

На практике наиболее распространен прямой метод стандартизации, который применяют в том случае, если известен возрастной состав населения и есть данные для расчета возрастных коэффициентов смертности (рождаемости). Этот метод состоит из трех этапов.

Первый этап: вычисление возрастных коэффициентов смертности (рождаемости) для каждой возрастной группы.

Второй этап: выбор стандарта возрастного состава населения. В качестве стандарта (базы сравнения) можно считать возрастную структуру населения любой территории, в частности одной из сравниваемых.

Третий этап: расчет стандартизованных коэффициентов.

Косвенный и обратный методы стандартизации применяются при отсутствии информации о возрастном составе умерших (родившихся) или о возрастной структуре населения. В настоящее время эти методы мало востребованы, поскольку в современном обществе имеется достаточно широкий доступ к получению данных для использования прямого метода стандартизации.

Для статистического анализа данных используют различные математико-статистические методы: выборочный метод и опенка параметров распределения, проверка статистических гипотез, корреляционно-регрессионный анализ, дисперсионный анализ, анализ временных рядов, анализ выживаемости и т.д. Статистические методы широко используются в доказательной медицине (от англ. evidence-based medicine — медицина, основанная на доказательствах). Это раздел медицины, основанный на доказательствах, посвящен поиску, сравнению, обобщению и распространению полученных результатов клинической практики для повышения эффективности и безопасности лечения больных.

Для выбора оптимального метода лечения конкретного пациента доказательная медицина использует как практический врачебный опыт, так и результаты доказательных клинических исследований. При этом проводимое исследование должно быть контролируемым, т.е. сравнение конечных результатов должно быть проведено в двух группах пациентов: группе активного лечения (в которой больные получают терапию лекарственным средством, эффективность которого оценивается) и контрольной группе пациентов (получающих плацебо, или лечения, эффективность которого уже доказана, или не получающих лечение вообще). Кроме того, исследование должно быть рандомизированным, т.е. распределение пациентов в экспериментальную и контрольную группы (формирование выборочных совокупностей) должно происходить методом случайного отбора. В настоящее время наиболее признанным методом рандомизации является использование генератора случайных чисел.

Для снижения роли субъективных факторов в проведении клинических исследований с использованием принципов доказательной медицины, как правило, применяют следующие методические подходы:

— слепое исследование (пациент не знает, получает он активное лечение или входит в группу контроля);

— двойное слепое исследование (о принадлежности пациента к той или иной группе не знает ни пациент, ни лечащий врач).

В клинических испытаниях в качестве основного критерия оценки должен использоваться клинический исход, который имеет существенное для больного значение и которого он хотел бы избежать (например, смерть, инфаркт миокарда, инсульт, перелом костей, потеря зрения, необходимость применения искусственной вентиляции легких и иные состояния, существенно снижающие качество жизни пациента).

Нередко в качестве критериев оценки эффективности вмешательства используют так называемые суррогатные исходы — лабораторные или выявляемые при физикальном исследовании показатели (снижение артериального давления при артериальной гипертензии, уменьшение признаков сердечной недостаточности, увеличение минеральной плотности кости при остеопорозе и т.п.). К сожалению, суррогатные исходы далеко не всегда коррелируют с клинически значимыми исходами. Практически значимые для доказательной медицины результаты могут быть получены только при когортном методе — длительном наблюдении за больными обычно в течение нескольких лет. Эти результаты создают фундамент доказательной медицины.

После статистического анализа переходят к логическому анализу и интерпретации полученных результатов.Во многом проведению логического анализа помогает визуализация данных путем построения графиков.

Для построения графиков используются различные прикладные пакеты компьютерных программ (MS Excel, STATISTICA, SPSS, IVlathCAD, Maple и др.). Целью построения статистических графиков является в первую очередь получение информации в наглядной и зрительно легко воспринимаемой форме. В частности, с помощью графиков можно проследить участки возрастания, убывания или стабильности каких-либо показателей.

Самым распространенным из них является диаграмма — изображение статистических данных посредством геометрических фигур либо символов. Диаграммы чаще используют в медико-социальных исследованиях, в то время как картограммы и картодиаграммы — в медико-географических. Диаграммы можно классифицировать различным образом. Так, по назначению принято различать диаграммы сравнения, структурные и динамические диаграммы, по форме отображения — линейные, столбиковые, ленточные, секторные круговые, секторные столбиковые, фигурные, радиальные или диаграммы в полярных координатах, диаграммы рассеяния, слоевые и др.

Заканчивается данный этап статистического исследования формулировкой выводов и предложений для выработки управленческих решений.