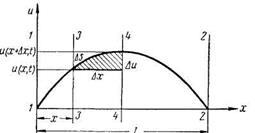
Рассмотрим совместное движение двух несжимаемых и взаимно нерастворимых жидкостей в трубе вдоль ее оси х (рис. 6). Будем считать, что движение происходит при постоянной температуре, т. е. процесс изотермический. Примером таких жидкостей могут быть нефть и вода. Выделим в трубе два сечения 1—1 и 2—2 соответственно ид расстоянии х и 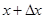 от начала оси х. Объем, заключенный между этими сечениями, обозначим через
от начала оси х. Объем, заключенный между этими сечениями, обозначим через  . В этом объеме находятся жидкости 1 и 2. Процесс рассматриваем в единицу времени или за промежуток времени
. В этом объеме находятся жидкости 1 и 2. Процесс рассматриваем в единицу времени или за промежуток времени  . Задаемся соотношением между объемами этих жидкостей. Отношение объема одной жидкости
. Задаемся соотношением между объемами этих жидкостей. Отношение объема одной жидкости  или другой
или другой 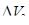 к объему, занимаемому обеими жидкостями
к объему, занимаемому обеими жидкостями 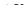 , называется насыщенностью и обозначается соответственно через
, называется насыщенностью и обозначается соответственно через 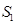 или S 2 (в долях или процентах).
или S 2 (в долях или процентах).
Обозначим плотность первой жидкости 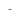 объем этой жидкости, проходящей через сечение 1—1 за единицу времени,
объем этой жидкости, проходящей через сечение 1—1 за единицу времени,  , и проходящей через сечение 2—2, — Q 12 . Для второй жидкости введем соответтвенно обозначения
, и проходящей через сечение 2—2, — Q 12 . Для второй жидкости введем соответтвенно обозначения 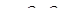 . Тогда масса первой жидкости, прошедшей через сечение 1— 1, будет
. Тогда масса первой жидкости, прошедшей через сечение 1— 1, будет 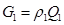 а масса второй жидкости
а масса второй жидкости  . В случае движения одной несжимаемой жидкости, т. е. когда S 1 = 1 (или S 2 = 0), Q 1 = Q 22 (или Q 2 = Q 22 ). Ввиду того, что в объеме
. В случае движения одной несжимаемой жидкости, т. е. когда S 1 = 1 (или S 2 = 0), Q 1 = Q 22 (или Q 2 = Q 22 ). Ввиду того, что в объеме 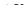 содержится объем
содержится объем  первой жидкости, объем
первой жидкости, объем 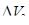
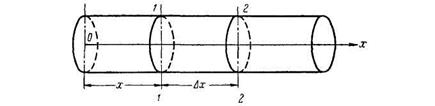
Рис. 6.
второй жидкости и соотношения их в объеме AV могут изменяться, то в общем случае
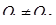 и
и 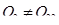 . (1.36)
. (1.36)
Поясним это на конкретном примере.
Пусть в объеме 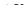 = 10 м3 нефтенасыщенность составляет 50%, т. е. в нем содержится 5 м5 воды. Количество жидкости, протекающей через сечение 1—1 (см. рис. 6) и вытекающей из сечения 2—2, может отличаться друг от друга. Так, если через сечение 1—1 поступает 2 м5 нефти, то через сечение 2—2 может быть отобрано 2 м3 нефти, а может быть больше или меньше, но не больше 7 м3 (суммы объема нефти в общем объеме и объема нефти, поступившей через сечение 2—2, должны быть равны объему нефти, поступающей в сечение 1—1). S 1 не изменяется во времени, т. е. процесс движения установившийся.
= 10 м3 нефтенасыщенность составляет 50%, т. е. в нем содержится 5 м5 воды. Количество жидкости, протекающей через сечение 1—1 (см. рис. 6) и вытекающей из сечения 2—2, может отличаться друг от друга. Так, если через сечение 1—1 поступает 2 м5 нефти, то через сечение 2—2 может быть отобрано 2 м3 нефти, а может быть больше или меньше, но не больше 7 м3 (суммы объема нефти в общем объеме и объема нефти, поступившей через сечение 2—2, должны быть равны объему нефти, поступающей в сечение 1—1). S 1 не изменяется во времени, т. е. процесс движения установившийся.
Если через сечение 2—2 отбирается нефти больше, чем втекает через сечение 1—1, то S 1 уменьшается. Так, если из сечения 2—2 отбирается 3 м3 нефти, а через сечение 1—1 поступает 2 м3, то
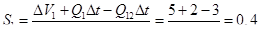 ,
,
т. е. нефтенасыщенность снизится на 11)%.
Если через сечение 1—1 поступает 1 м3 воды, то из сечения 2—2 может быть отобрана вода в количестве, равном, большем или меньшем чем 1 ма, но в соответствии с поступившим в сечение 1—1 и отобранном из сечения 2—2 объемом нефти, т. е. должен быть соблюден следующий баланс: 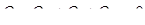
Следовательно, для рассмотренного примера
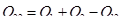 = 2+ 1-3 = 0.
= 2+ 1-3 = 0.
Таким образом, ввиду несжимаемости жидкостей сумма их объемов, поступивших в сечение 1—1, равна сумме объемов жидкостей, вытекающих из сечения 2—2,
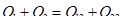 (1-37)
(1-37)
Формула (1.37) отражает закон постоянства массы в конечной форме.
Масса каждой жидкости, а также сумма их масс в объеме 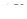 во времени не постоянна. Так, в приведенном выше примере объем нефти в объеме
во времени не постоянна. Так, в приведенном выше примере объем нефти в объеме 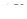 станет равным 4м3,а объем воды — 6м3. При
станет равным 4м3,а объем воды — 6м3. При  = 800 т/м3 и
= 800 т/м3 и 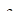 =1000 1/м3 первоначальная масса жидкостей, находящихся в объеме
=1000 1/м3 первоначальная масса жидкостей, находящихся в объеме 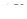 , составляла G ( t ) = (0,8*5 + 1*5) = 9 т.
, составляла G ( t ) = (0,8*5 + 1*5) = 9 т.
После прохождения отмеченных объемов жидкостей через некоторое время 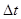 масса их в том же объеме составит
масса их в том же объеме составит 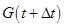 = 0,8*4+l*6 = 9,2т. Следовательно, вес жидкости в объеме
= 0,8*4+l*6 = 9,2т. Следовательно, вес жидкости в объеме 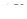 увеличивается на 0,2 т. Разность между массой жидкости, втекающей через сечение 1—1 и вытекающей через сечение 2—2, идет на изменение насыщенности в объеме
увеличивается на 0,2 т. Разность между массой жидкости, втекающей через сечение 1—1 и вытекающей через сечение 2—2, идет на изменение насыщенности в объеме 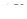 .
.
 , (I.38)
, (I.38)
где  — изменение нефтенасыщенности (в приведенном выше примере
— изменение нефтенасыщенности (в приведенном выше примере  = 10%).
= 10%).
Рассмотрим процесс совместного движения двух жидкостей,, характеризующийся величинами Q 1 Q 2 , S 1 и S2, которые меняются; как вдоль оси х, так и во времени.
Запишем уравнения (1.37) и (1.38) для любого сечения и в любой момент времени. Процесс исследуется в интервале  х за промежуток времени
х за промежуток времени 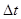 . Чтобы получить выражения (1.37) и (1.38) для любого сечения и в любой момент времени, необходимо, чтобы
. Чтобы получить выражения (1.37) и (1.38) для любого сечения и в любой момент времени, необходимо, чтобы 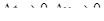 .
.
В приведенном примере Q 1 и Q 12 принимались (и в дальнейшем принимаются) постоянными во времени, но они могут быть и переменными.
Таким образом, для первой жидкости в сечении 1—1 имеем (  , а в сечении 2—2
, а в сечении 2—2 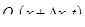 , соответственно для второй жидкости имеем (
, соответственно для второй жидкости имеем ( 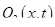 2 (х, t ) и
2 (х, t ) и 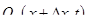 . Следовательно,
. Следовательно,
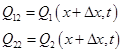
В момент времени t в сечении 1—1 насыщенность будет S 1 (х, t ), через промежуток времени 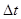 насыщенность станет
насыщенность станет 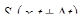 , а в сечении 2—2 соответственно
, а в сечении 2—2 соответственно  и
и 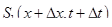 . Запишем закон постоянства массы (1.37) для данного элементарного объема
. Запишем закон постоянства массы (1.37) для данного элементарного объема
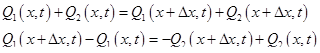 .
.
Разделим на  и перейдем к пределу при
и перейдем к пределу при  .
.
Выражение (1.40) представляет собой закон постоянства массы в дифференциальной форме.
 ,
,
или
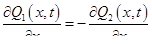 , (1.39)
, (1.39)
или
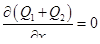 , (1.40)
, (1.40)
 , (1.41)
, (1.41)
где
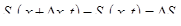
Запишем выражение (1.38) для элемента объема 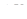
Здесь 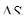 — изменение насыщенности во времени из-за накопления первой жидкости.
— изменение насыщенности во времени из-за накопления первой жидкости.
Отметим, что  будут иметь одинаковые значения при
будут иметь одинаковые значения при  . Следовательно, изменение насыщенности
. Следовательно, изменение насыщенности 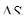 в объеме
в объеме 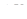 (при
(при  можно выразить как
можно выразить как  , так и
, так и  .
.
В выражении (1.41) левая часть умножена на 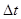 , так как масса жидкости G отнесена к единице времени, а процесс рассматривается в течение времени
, так как масса жидкости G отнесена к единице времени, а процесс рассматривается в течение времени 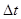 .
.
Если масса первой жидкости в объеме 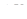 увеличивается, то накопление имеет положительный знак
увеличивается, то накопление имеет положительный знак
 .
.
Это может быть в случае, если  , т. е. масса первой жидкости, поступающей через сечение 1—1, больше отбора ее через сечение 2—2. Поэтому в (1.41) знак в правой части должен быть противоположным знаку в левой части, т. е.
, т. е. масса первой жидкости, поступающей через сечение 1—1, больше отбора ее через сечение 2—2. Поэтому в (1.41) знак в правой части должен быть противоположным знаку в левой части, т. е.
 (1.42)
(1.42)
или, зная, что 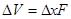 ,
,
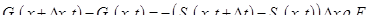 (1.43)
(1.43)
Разделив обе части (1.43) на 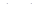 и перейдя к пределу при
и перейдя к пределу при

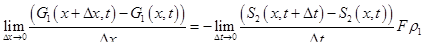
откуда для первой жидкости, получим
 (1.44)
(1.44)
или
 (1.45)
(1.45)
Для второй жидкости аналогично

(1.46)
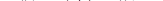
(1.47)
Заметим, что (1.44), (1.45) и (1.40) являются независимыми уравнениями, а (1.46) и (1.47) могут быть получены из них. Или формула (1.40) может быть получена из уравнений (1.44), (1.45), (1.46), (1.47). Покажем это на примере.
Сложив (1.45) и (1.47), получим
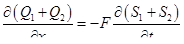 (1.48)
(1.48)
Так как  , то
, то

Откуда
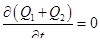
Как было отмечено выше, в рассматриваемом примере необходимо определить Q 1 Q 2 и S1 Зная же S 1 , можно определить S 2 = 1— S 1 , т. е. для трех величин имеется два уравнения (1.45) и (1.47).
Рассмотрим движение смеси жидкости и растворенного в ней газа и выделенном объеме трубы (см. рис. 6). Будем считать, что движение происходит при постоянной температуре, т. е. процесс изотермический. Принимается, что жидкость несжимаема, а газ, как обычно, сжимаем.
В данном случае через сечение 1—1 поступают жидкость с растворенным в ней газом и газ в свободном состоянии. В объеме  имеется насыщенность газом и жидкостью. Причем насыщенность газом в отличие от предыдущего случая может изменяться как в результате изменения количества газа в этом объеме, так и вследствие его сжимаемости.
имеется насыщенность газом и жидкостью. Причем насыщенность газом в отличие от предыдущего случая может изменяться как в результате изменения количества газа в этом объеме, так и вследствие его сжимаемости.
Обозначения приняты те же, что и в предыдущем случае, но вместо первой жидкости взят свободный газ, а вместо второй — насыщенная газом жидкость.
Введем следующие дополнительные обозначения для масс газа и жидкости: G 3 — масса газа в растворенном состоянии, поступающего через сечение 1—1 за единицу времени; G 32 — масса газа в растворенном состоянии, выходящего через сечение 2—2 за единицу времени; G4 — масса растворенного газа в единице объема жидкости за единицу времени.
Принимаем, что масса растворенного в жидкости газа, по сравнению с массой самой жидкости очень мала. Поэтому ею можно пренебречь, т. е. G2 и G22 рассмотрим как массу жидкости. Но это предположение не всегда справедливо. Для иллюстрации этого приведем следующий пример. Пусть имеется нефть, плотность которой (при 20° С) 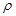 = 780 кг/м3, и газ, относительная плотность которого (по воздуху) Δ = 0,7; газовый фактор Г = 100 м3/м3.
= 780 кг/м3, и газ, относительная плотность которого (по воздуху) Δ = 0,7; газовый фактор Г = 100 м3/м3.
Относительная молекулярная масса газа будет
М1 = М3 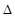 = 29-0,7 = 20,3,
= 29-0,7 = 20,3,
где М3 — молекулярный вес воздуха.
Число киломолей газа, растворенных в 1 м3 нефти,
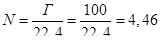 '
'
где 22,4 м3 — объем 1 кмоль газа при нормальных условиях.
Кажущаяся плотность газа (при относительной плотности 0,7) в нефти (плотность 780 кг/м3)  = 320 кг/м3. Следовательно, увеличение объема 1 м3 нефти, вызванное растворением газа, составит
= 320 кг/м3. Следовательно, увеличение объема 1 м3 нефти, вызванное растворением газа, составит
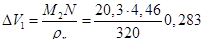 м3.
м3.
Общий объем насыщенной газом нефти, отнесенной к атмосферным условиям, будет
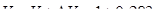 м3
м3
а, масса нефти с растворенным в пей газом
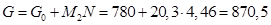 кг,
кг,
где Go — вес ненасыщенной нефти; V — объем ненасыщенной нефти. Плотность нефти с растворенным в ней газом рассчитывается по формуле
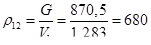 кг/м3.
кг/м3.
Следовательно, при растворении газа в жидкости масса ее увеличивается.
Рассмотрим изменение массы жидкости в элементарном объеме, т. е. запишем закон постоянства масс жидкости (по аналогии с предыдущим случаем)
 . (I.49)
. (I.49)
Запишем закон постоянства массы для газовой фазы. Изменение массы газа за время 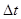 — разность массы газа, поступающего через сечение 1—1 (см. рис. 6), и массы газа, выходящего из сечения 2—2, т. е.
— разность массы газа, поступающего через сечение 1—1 (см. рис. 6), и массы газа, выходящего из сечения 2—2, т. е.  , соответствует изменению массы газа в рассматриваемом объеме и равно сумме изменения масс растворенного и свободного газа в объеме
, соответствует изменению массы газа в рассматриваемом объеме и равно сумме изменения масс растворенного и свободного газа в объеме  , т. е. равно
, т. е. равно  .
.
Таким образом, можно записать
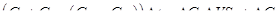 l . (I.49)
l . (I.49)
В соответствии с ранее принятым (в предыдущем случае) 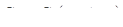 .
.
Изменение G 1 происходит в результате изменения 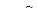 . Следовательно,
. Следовательно,  .
.
Для того чтобы уравнения (1.49) и (1.49') записать для любого момента времени и для любого сечения, проделаем следующее.
Запишем уравнение (1.49), согласно принятым обозначениям, в виде
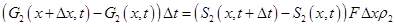 . (1.50)
. (1.50)
Если масса жидкости в объеме  увеличивается, то накопление имеет положительный знак, т. е.
увеличивается, то накопление имеет положительный знак, т. е.  . Это может быть при
. Это может быть при 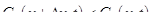 , т. е. когда масса жидкости, поступающей в сечение
, т. е. когда масса жидкости, поступающей в сечение
1—1, больше массы жидкости, отбираемой из сечения 2—2. Поэтому в (1.50) знак в правой части должен быть противоположным знаку в левой части
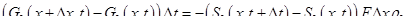 (1.51)
(1.51)
Разделив обе части (1.51) на  и
и 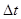 и перейдя к пределу при
и перейдя к пределу при 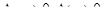 , получим
, получим
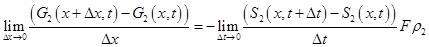

(1.52)
Из уравнения (1.49') имеем
 (1.53)
(1.53)
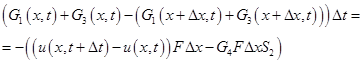 (1.54)
(1.54)
Разделив обе части уравнения (1.54) на 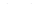 и перейдя к пределу при
и перейдя к пределу при 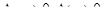

или
 (1.55)
(1.55)
Объем жидкости, поступающей в сечение 1—1, будет —. 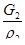 .Следовательно, в объеме
.Следовательно, в объеме 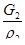 — содержится масса растворенного газа
— содержится масса растворенного газа 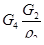 , т. е.
, т. е.
 . (I.56)
. (I.56)
Таким образом, в трех уравнениях (1.52), (1.55) и (1.56) имеются неизвестные: Gx , G 2 , G 3 , G4, S 2 и  .
.
Приведенному выше примеру аналогичен случай движения газо-конденсатной смесив трубах или в пористой среде. В газоконденсатной системе в отличие от газонефтяной при снижении давления выпадает жидкость-конденсат. Следовательно, в выделенный объем поступает газ с конденсатом. Принимая, что выпавший конденсат неподвижен, и пренебрегая изменением массы газа от выпадения конденсата, можно применить закон постоянства массы для определения измене-ния насыщенности конденсатом рассматриваемого объема.
Через сечение 1—1 в единицу времени прошли масса газа G 1 и масса конденсата G2. Через сечение 2—2 отобраны масса газа  и масса конденсата G22. Тогда масса конденсата, накопившегося в объеме в единицу времени,
и масса конденсата G22. Тогда масса конденсата, накопившегося в объеме в единицу времени,
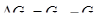 .
.
Это приращение массы конденсата приведет при условии несжимаемости конденсата ( 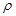 = const) к изменению объема в единицу вре мени на величину
= const) к изменению объема в единицу вре мени на величину  .
.
За отрезок времени 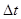 изменение объема будет
изменение объема будет 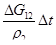 . Это изменение объема приведет к изменению насыщенности конденсатом на величину
. Это изменение объема приведет к изменению насыщенности конденсатом на величину  .
.
Аналогично предыдущему случаю запишем
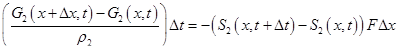 (1.57)
(1.57)
Знак минус перед правой частью поставлен, исходя из следующих соображений: если  , то насыщенность конденсата в объеме
, то насыщенность конденсата в объеме  уменьшается, т. е.
уменьшается, т. е.  , и наоборот.
, и наоборот.
Разделив обе части уравнения (1.57) на  и
и 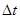 и перейдя к пределу при
и перейдя к пределу при  , получим
, получим

(1.58)
Так как было принято, что масса газа не изменяется при выпадении конденсата, то для газовой фазы можно написать закон постоянства массы в форме, записанной выше,

(1.59)
В уравнениях (1.58) и (1.59), описывающих процесс движения газоконденсатной системы, имеются четыре неизвестных.
Закон сохранения энергии
Рассмотрим некоторые примеры применения закона сохранения энергии для механических и тепловых процессов.
Как известно, для механических процессов сумма кинетической и потенциальной энергии постоянна.
А для тепловых процессах закон сохранения энергии отражается в виде первого закона термодинамики, который формулируется следующим образом: бесконечно малое изменение внутренней энергии состоит из двух частей — из количества тепла, полученного телом, и произведенной телом работы.
Работа при поступлении тепла зависит от начального и конечного состояния тела и от пути, по которому изменяется состояние тела. В связи с этим нельзя рассматривать тепловой эффект процесса как разность этих количеств в конечном и начальном состояниях.
С поглощением тепла в количестве dQ температура повышается на величину dT . Отношение  (где т — масса тела) называется теплоемкостью тела. В физике пользуются теплоемкостью при постоянном давлении ср и теплоемкостью при постоянном объеме
(где т — масса тела) называется теплоемкостью тела. В физике пользуются теплоемкостью при постоянном давлении ср и теплоемкостью при постоянном объеме  .
.
Применяя первый закон термодинамики для исследования процесса распространения тепла в теле, ограниченном сечениями сечения 1—1 и 2—2 (рис. 7) получим балансовое равенство для теплот. Пусть тело имеет какую-то определенную начальную температуру. К одному концу тела подводится источник тепла или холода. Соответственно этому в теле происходит нагревание или охлаждение.
Температура в какой-либо точке тела будет зависеть от расстояния точки до места подвода тепла и времени
Т = Т(х, t ).
На текущее распределение температуры в теле оказывает влияние начальное распределение температуры, а также условия в концевых сечениях тел, в частности от температуры на обоих концах тела.
В приведенном примере через сечение 1—1 в единицу времени подводится количество тепла, равное Q (х, t ). Через сечение 2—2 в единицу времени отводится количество тепла, равное 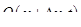 . Разность между этими количествами тепла
. Разность между этими количествами тепла
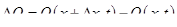 (1.60)
(1.60)
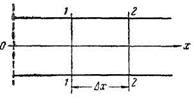 Рис.
Рис.
в соответствии с первым законом термодинамики затрачивается на изменение температуры в отсеке между сечениями 1—1 и 2—2.
Если  , то тело нагревается, в противном случае — охлаждается, т. е. в первом случае
, то тело нагревается, в противном случае — охлаждается, т. е. в первом случае
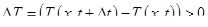 ,(1.61)
,(1.61)
а во втором — 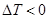 .
.
При изменении количества подводимого и отводимого тепла па величину 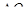 температура тела (в соответствии с законом сохранения энергии и определением теплоемкости) должна изменяться на величину
температура тела (в соответствии с законом сохранения энергии и определением теплоемкости) должна изменяться на величину
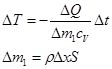 (1.62)
(1.62)
где 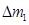 — элементарная масса тела; S — площадь поперечного сечения тела;
— элементарная масса тела; S — площадь поперечного сечения тела; 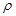 — плотность тела.
— плотность тела.
Так как 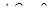 при
при 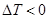 и
и 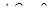 при
при  , то в правой части (1.62) поставлен знак минус.
, то в правой части (1.62) поставлен знак минус.
Подставив в (1.62) значения 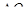 и
и  соответственно из (1.60), (1.61) н разделив его на
соответственно из (1.60), (1.61) н разделив его на  и перейдя к пределу при
и перейдя к пределу при  ,
,
получим
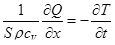 (1.63)
(1.63)
Таким образом, в одном уравнении получаем два неизвестных Q и Т.
Рассмотрим, каким образом можно получить недостающие уравнения. Например, для движения смеси двух несжимаемых жидкостей необходимо составить еще одно уравнение. Но в этом случае процесс определяется и давлением. Поэтому необходимо иметь два уравнения для нахождения Q 1 и Q 2 .
При изотермическом совместном движении газа и жидкости в трубопроводе неизвестными были 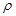 и V , а уравнение — одно. Но, как известно,
и V , а уравнение — одно. Но, как известно, 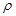 связано с давлением при помощи уравнения состояния Клайперона — Менделеева
связано с давлением при помощи уравнения состояния Клайперона — Менделеева
 ,
,
где р — давление.
Однако при этом появляется новое неизвестное р, т. е. опять не хватает одного уравнения. Приведенное выше уравнение соответствовало закону постоянства массы. Для исследуемого явления необходимо применить еще закон сохранения энергии, например в виде уравнения Бернулли. Но в этом случае появится новое неизвестное — работа сил трения, т. е. требуется опять одно уравнение для определения силы трения. Это уравнение устанавливается экспериментально.
Для совместного движения несжимаемых жидкостей закон сохранения энергии приводит также к необходимости определения силы трения. Указанный процесс характеризуется и давлением. Поэтому и в этом случае необходимо экспериментально составить одно уравнение для сил трения. Если движение неизотермическое, то следует применить и первый закон термодинамики. Тогда появятся два неизвестных Q и Т, связанных одним уравнением типа
 ,
,
т. е. и в этом случае необходимо определить одну экспериментальную зависимость для Q .
При изотермическом движении газированной жидкости в трубопроводе или при фильтрации газированной жидкости в пористой среде плотность газа р связана с давлением р. Появляется еще одно неизвестное р. Вводя понятие массовой скорости для жидкости w 1 и газа w 2 , можно через них вычислить соответственно G 1 и G 2 . Неизвестными в этом случае являются  . Таким образом, необходимо экспериментально определить зависимости для w 1 , w 2 и G 3 .
. Таким образом, необходимо экспериментально определить зависимости для w 1 , w 2 и G 3 .
При использовании закона сохранения энергии в этом случае необходимо знать работу силы трения, т. е. силу трения (новое неизвестное), причем применение закона сохранения энергии не уменьшает числа недостающих уравнений. Наоборот, количество уравнений увеличивается, соответственно этому увеличивается и количество неизвестных. При движении газоконденсатной смеси в трубах или в пористой среде имеем два уравнения и четыре неизвестных 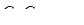 . Плотность р1 связана с давлением при помощи уравнения состояния.
. Плотность р1 связана с давлением при помощи уравнения состояния.
Таким образом, необходимо экспериментально определить две зависимости — для G 1 и G 2 .
При исследовании процесса распространения тепла в теле имеем два неизвестных Q и Т и одно уравнение. Закон постоянства массы выполняется тождественно и недостающее уравнение для Q определяется экспериментально.
Пример Движения в круглой цилиндрической трубе вдоль кольца.
Покажем применение закона сохранения механической энергии. Обозначим через 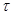 — касательное напряжение. Выведем дифференциальное уравнение движения в круглой цилиндрической трубе вдоль кольца. Для этого выделим в зоне на расстоянии
— касательное напряжение. Выведем дифференциальное уравнение движения в круглой цилиндрической трубе вдоль кольца. Для этого выделим в зоне на расстоянии 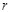 от оси трубы элементарный кольцевой слой толщиной dr и длиной
от оси трубы элементарный кольцевой слой толщиной dr и длиной  и составим уравнение равновесия сил, действующих на выделенный элемент. Этими силами будут: тормозящая сила
и составим уравнение равновесия сил, действующих на выделенный элемент. Этими силами будут: тормозящая сила  , ускоряющая сила
, ускоряющая сила  , сила давления
, сила давления 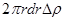 и сила инерции
и сила инерции  .
.
По принципу Д'Аламбера, сумма этих сил должна равняться нулю. Если при этом учесть, что первая и последняя из этих сил действуют в направлении, обратном действию остальных двух сил, то
 (1.64)
(1.64)
|
|
Пренебрегая величиной drdx по сравнению с другими членами, получаем
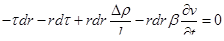 (1.65)
(1.65)
|
|
Рис.8.
Пример Вывод уравнения колебаний натянутой упругой струны на основе закона сохранения энергии.
Колебания принимаются малыми, что позволяет пренебречь увеличением длины струны и приводит к постоянству натяжения в любом сечении и в любой момент времени. Пренебрегаем трением, т. е. диссипация (рассеяние) энергии принимается равной нулю (так как приток энергии извне принимается равным нулю). Предполагаем, что начальный момент времени соответствует состоянию равновесия. Например, в начальный момент времени струна натянута, находится в горизонтальном положении и концы ее закреплены. Для того чтобы начался процесс колебания струны, необходимо ее вывести из положения равновесия, положим, начальным импульсом. Обозначим отклонение струны от ее положения равновесия через  .
.
На рис. 8 цифрами 1—1 и 2—2 обозначены сечения, в которых закреплены концы струны. Выделим на расстоянии х от начала оси х элементарный отрезок струны  между сечениями, обозначенными цифрами 3—4.
между сечениями, обозначенными цифрами 3—4.
Для определения кинетической энергии необходимо найти скорость точек этого отрезка струны. Смещение (отклонение от положения равновесия) точки 3 будет  а через интервал времени
а через интервал времени 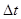 оно составит
оно составит 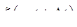 .
.
Средняя скорость этой точки равна
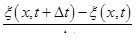 (1.66)
(1.66)
Мгновенная скорость в точке x определяется при 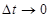 соотношением
соотношением
 .
.
Учитывая, что масса отрезка струны  , где
, где 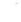 линейная плотность, получим изменение кинетической энергии элемента
линейная плотность, получим изменение кинетической энергии элемента 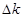 имеет вид
имеет вид
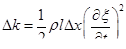 или в дифференциалах
или в дифференциалах 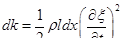 . Суммируя по длине получим
. Суммируя по длине получим
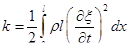 (1.67)
(1.67)
Получим аналогичным образом соотношение для потенциальной энергии
 (1.68)
(1.68)
Применяя известную из курса математики формулу длины дуги кривой , получим
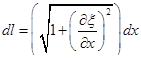 .
.
Тогда
 ,
,
или
 .
.
Используя для корня разложение в ряд Маклорена биномального выражения, и ограничиваясь квадратичными членами получим
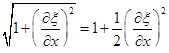
и выражение для потенциальной энергии для всей струны
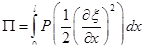 .
.
Поскольку сумма потенциальной и кинетической энергии составляет постоянную величину равную полной энергии получим  .
.
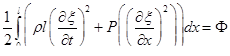 .
.
Продифференцируем по t
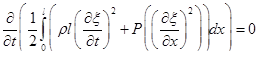
или

Продифференцируем как сложную функцию в подинтегральном выражении, тогда получим
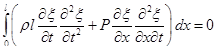 (1.74)
(1.74)
или интегрируя по частям второе слагаемое и учитывая, что концы струны жестко закреплены т.е. перемещения в начале и конце струны равны нулю

получим
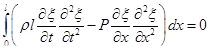 (1.75)
(1.75)
Учитывая, что выражение под знаком интеграла не отрицательно, то интеграл равен нулю в том случае, когда подынтегральная функция равняется нулю.
 (1.76)
(1.76)
Отсюда, поскольку 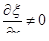 , можно разделить левую и правую части уравнения на
, можно разделить левую и правую части уравнения на 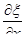 . Тогда получим
. Тогда получим
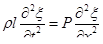 . (1.77)
. (1.77)
Это равенство представляет собой дифференциальное уравнение колебаний струны. Отметим, что здесь одно уравнение и одна неизвестная функция – поперечное перемещение струны. Натяжение струны было принято постоянным, поэтому оно исключено как неизвестное.
Пример
Рассмотрим продольное колебание трубы, которое происходит в процессе спуска-подъема бурильных труб или же в процессе непосредственного бурения. Так, например, если имеется шарошечное долото, которое в процессе бурения производит колебательное движение, то в упругих бурильных трубах возникает продольное колебание.
Способ бурения принимается турбинным, так как при роторном в бурильных трубах возникают крутильные колебания, вызванные вращением инструмента. Чтобы не усложнять вывода, трением пренебрегаем. Дифференциальное уравнение в этом случае имеет такой же вид, как и для колебания струны. Но в отличие от колебания струны при продольном колебании упругие напряжения, возникающие в каждом сечении, уже не могут быть приняты постоянными как в сечениях, так и во времени.
Дифференциальное уравнение для этого случая можно получить из уравнения движения.
В данном продольном стержне смещение происходит вдоль оси.
Обозначим через 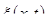 смещение вдоль оси ох (см. рис. 9).
смещение вдоль оси ох (см. рис. 9).
Скорость вдоль оси Ox

Тогда ускорение вдоль оси Ox имеет вид

Рис.10
Упругое напряжение в сечении 1—1 в момент времени t будет F ( x , t ), а в сечении 2— 2 — будет  .
.
Согласно второму закону Ньютона можно записать

или
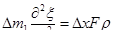 (1.78)
(1.78)
где 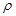 — плотность; F — площадь поперечного сечения стержня. Разделив уравнение (1.78) на Δх и перейдя к пределу при
— плотность; F — площадь поперечного сечения стержня. Разделив уравнение (1.78) на Δх и перейдя к пределу при 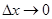 , получим
, получим
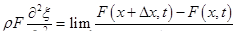 (1.79)
(1.79)
 (1.80)
(1.80)
Таким образом, имеем одно уравнение и два неизвестных 
 и F .
и F .
Данные уравнения можно получить также, исходя из закона сохранения энергии.
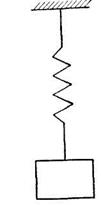
Пример Вывод уравнения колебания груза на упругой нити на основе закона сохранения энергии.
Рассмотрим колебание груза, подвешенного к упругой нити. Примем, что сила упругости пропорциональна удлинению х (рис. 10).
На рис. 10 показаны: 1 — положение равновесия, 2 — отклонение от положения равновесия, которое изменяется в зависимости от времени. Если в начальный момент времени груз находится в положении равновесия, то х = 0.
Кинетическая энергия в положении 2 равна 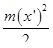 , где т —масса;
, где т —масса; 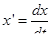 - скорость груза.
- скорость груза.
Потенциальная энергия — это энергия упругости нити. Силы упругости приняты пропорциональными х, т. е. кх совершает элементарную работу kxdx , соответствующую элементарной потенциальной энергии. В положении 2 потенциальная энергия определяется как
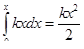 .
.
Отсюда
 , (1.81)
, (1.81)
где Ф — полная энергия в положении 2. Дифференцируя (1.81) по t , получаем
тх"х' + кхх' = 0.
При 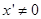
тх" + кх = 0. (1.82)
Уравнение (1.82) и есть выражение второго закона Ньютона.
Во всех приведенных случаях, как правило, число неизвестных было больше числа уравнений, за исключением одного случая — поперечного колебания струны. Однако и в последнем, как было отмечено, одно неизвестное — натяжение струны — исключили, приняв его постоянным.
Пример Продольное колебание стержня
Для продольного колебания стержня закон постоянства массы также выполняется тождественно и не дает нового уравнения. В этом случае недостает одного уравнения для вычисления упругих напряжений, которое находят экспериментально.
Для механических процессов необходимы данные о характерных свойствах рассматриваемой сплошной среды. Эти свойства описываются так называемым определяющим уравнением, которое представляет собой уравнение, описывающее механическую модель.
Ниже будут рассмотрены различные механические модели.
В связи с тем, что тепловые и диффузионные процессы приобретают все большее значение в нефтяной промышленности, будут рассмотрены недостающие уравнения при описании этих процессов. Метод моделирования широко применяется в различных отраслях промышленности, в частности в нефтяной. Учитывая это, а также необходимость расчета электрических и магнитных цепей для различных задач нефтедобычи и бурения, в специальном параграфе рассматриваем основные законы электричества и магнетизма. В заключение этой главы приведем еще одно необходимое уравнение состояния — скалярное соотношение между плотностью, давлением и температурой.
Для некоторых механических задач часто берут такое уравнение состояния, которое не содержит температуры. Процессы, подчиняющиеся таким уравнениям состояния, называются баротропными.
Однородная несжимаемая жидкость представляет частный случая баротропной жидкости.
Важным частным случаем являются изотермические процессы, при которых температура сохраняется постоянной, и адиабатические процессы, при которых отсутствует теплообмен.
Анализ размерности
Анализ размерностей, теория подобия, моделирование, а также метод аналогии различных явлений позволяют, наряду с правильной постановкой и проведением экспериментов, ускорить вычислительные и другие работы. Однако в теоретических основах бурения нефтяных и газовых скважин этот метод широко не применяется. В то же время в теоретических основах разработки нефтяных и газовых залежей эти средства сравнительно широко применяются.
Для правильной постановки экспериментов, обработки получаемых результатов и обобщений нужно проводить количественно-теоретический анализ. В этом случае уменьшается количество опытов, результаты которых выражаются в безразмерных параметрах. В гидродинамике, в частности, эти параметры определяются, как соотношение сил.
Обычно различают величины размерные и безразмерные. Примерами размерных величин являются скорость, давление, вязкость, предельное напряжение сдвига, длина, время и др.
Отношения длины к ее диаметру, сил вязкости к предельному напряжению сдвига и т. д. являются безразмерными величинами. Анализ теории размерностей позволяет в уравнениях путем перехода от размерных переменных к безразмерным уменьшить число переменных. Допустим, что дано следующее квадратное уравнение:
ax 2 + bx + c = 0,
где безразмерный х зависит от коэффициентов а, b и с, имеющих одинаковые размерности.
Если все члены уравнения разделить на с, то уравнение примет вид
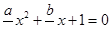
Как видно из уравнения, переменная х зависит от 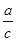 и
и 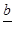 , т. е.
, т. е.
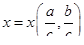 . Следовательно, запись уравнения в безразмерном виде
. Следовательно, запись уравнения в безразмерном виде
позволяет уменьшить число переменных с трех до двух. Если уравнение неизвестно или необходимо определить вид функциональной зависимости, то вместо изменения а и b изменим отношения 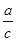 и
и 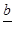 . Таким образом, не только уменьшается число переменных, но и при наименьших затратах времени и труда достигается возможность проведения эксперимента. Допустим, что для постановки эксперимента требуется изменение величин
. Таким образом, не только уменьшается число переменных, но и при наименьших затратах времени и труда достигается возможность проведения эксперимента. Допустим, что для постановки эксперимента требуется изменение величин 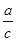 и
и 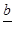 . Если во время экспериментирования величину с легко изменить, то, изменив величину с, можно изменить величины
. Если во время экспериментирования величину с легко изменить, то, изменив величину с, можно изменить величины 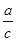 и
и 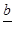 (при этом величины а и b остаются постоянными), и, наоборот, если трудно изменить величину с при экспериментировании, то, изменив величины
(при этом величины а и b остаются постоянными), и, наоборот, если трудно изменить величину с при экспериментировании, то, изменив величины 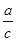 и
и 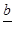 , можно изменить величины a и b . Если же
, можно изменить величины a и b . Если же
при проведении экспериментов сложно изменить величины b ис, то изменением одной из них можно достигнуть изменения отношения величин.
Физические основы связывают величины определенными зависимостями. Поэтому, если для некоторых величин будут выбраны размерности, то на основании соответствующих формул могут быть получены размерности других величин. Зависимость между физическими величинами позволяет выбрать такую основную систему размерностей, что для измерения в этой системе механических величин достаточен произвольный выбор трех размерностей.
Во многих случаях в технике единицы длины L , времени Т и силы F принимаются за основные единицы. Однако среди единиц измерения вязкость 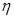 , скорость v и плотность
, скорость v и плотность 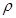 также могут быть приняты за основные. Такие величины называются величинами с независимыми размерностями (см. ниже).
также могут быть приняты за основные. Такие величины называются величинами с независимыми размерностями (см. ниже).
В настоящее время принята международная система единиц СИ, в которой размерность длины 1 м, массы — 1 кг и времени — 1 сек.
Если обозначить независимые размерности длины, времени и силы соответственно через L , Т и F , то широко применяемые в гидромеханике величины будут иметь размерности в таблице :
Таблица
| № | Название | соотношение |
| 1 | скорость | 
|
| 2 | ускорение | 
|
| 3 | угловая скорость | 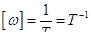
|
| 4 | вязкость | 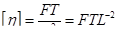
|
| 5 | Предельное напряжение сдвига | 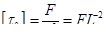
|
| 6 | давление | 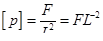
|
| 7 | плотность | 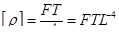
|
| 8 | Удельный вес | 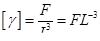
|
| 9 | масса | 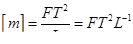
|
Если для математического описания нельзя составить дифференциальное уравнение или другую математическую зависимость, то, применяя теорию размерностей, можно описать физическое явление без уравнения, описывающего процесс. Но для этого необходимо знать поясняющие данное явление начальное и граничные условия. Применение для этих целей 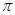 -теоремы (теоремы Букингема) позволяет выявить основные безразмерные параметры, характеризующие рассматриваемое явление.
-теоремы (теоремы Букингема) позволяет выявить основные безразмерные параметры, характеризующие рассматриваемое явление.
Предположим, что безразмерная величина а зависит от не зависящих друг от друга переменных величин а1: ..., ап
а = а(а1, а2, a 3 , . . ., ат, ат+1, . . ., ап).
Функциональная зависимость обычно записывается в виде  ; при большом количестве зависимостей
; при большом количестве зависимостей  . Знаки функции должны приниматься различными. Проще зависимости изображаются так:
. Знаки функции должны приниматься различными. Проще зависимости изображаются так: 
Допустим, что среди этих размерных величин число величин с независимыми размерностями равно т. В механике и технике их не может быть более трех. За независимые размерности принимаются длина L , время Т, сила F или же их степенная комбинация, из которой могут быть получены L , Т и F , например:
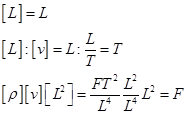
В уравнение входят n+1 размерных величин. На основании 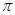 -теоремы связь между п + 1 размерными единицами может быть осуществлена п + 1 — m безразмерными параметрами, состоящими из п + 1 размерных величин.
-теоремы связь между п + 1 размерными единицами может быть осуществлена п + 1 — m безразмерными параметрами, состоящими из п + 1 размерных величин.
Тогда безразмерные параметры можно записать
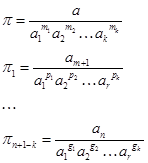
Здесь показатели т1,т2, ..., mk ; p 1 р2, ,.., pk ; g 1 g 2..., gk выбираются так, чтобы параметры 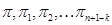 получились в безразмерном виде.
получились в безразмерном виде.
Применение 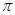 -теоремы поясним на конкретном примере. Предположим, что вместо величины
-теоремы поясним на конкретном примере. Предположим, что вместо величины 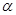 дана
дана  , а вместо величин с независимыми размерностями даны
, а вместо величин с независимыми размерностями даны 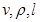 . Тогда получим
. Тогда получим
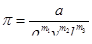
Так как в этой формуле левая часть 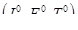 безразмерная, то и правая часть должна быть безразмерной, т. е.
безразмерная, то и правая часть должна быть безразмерной, т. е.
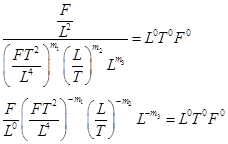
Тогда, приравнивая показатели степени при L , Т и F , получаем:

Решения этой системы трех линейных уравнений будут следующие:

Следовательно, безразмерный параметр можно представить в виде
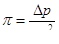
Это выражение представляет собой отношение давления и инерции и называется параметром Эйлера.
При использовании теории размерности используются физические и математические соображения.
Рассмотрим стационарное движение несжимаемой вязко-пластической жидкости в цилиндрической трубе. Перепад давления на концах трубопровода зависит от длины и диаметра трубы, структурной вязкости, предельного напряжения сдвига, плотности жидкости, а также от ускорения силы тяжести и скорости движения. При движении сжимаемой жидкости в уравнение должен войти не перепад давления, а абсолютные значения давлений, действующих на концах трубы. Для рассматриваемого случая физическое уравнение имеет вид
 , или
, или 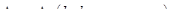 .
.
Так как число независимых равно трем, то, используя 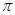 -теорему, можем вывести пять безразмерных параметров. В данном случае в качестве величин с независимыми размерностями могут быть выбраны следующие:
-теорему, можем вывести пять безразмерных параметров. В данном случае в качестве величин с независимыми размерностями могут быть выбраны следующие:  и т. д.
и т. д.
Выше было отмечено, что в каждом варианте величины с независимыми размерностями нужно выбирать так, чтобы их степенные комбинации дали бы возможность получить размерности длины L , силы F , времени Т. Теперь для принятых вариантов проверим это условие.
Так как в первом варианте давление, диаметр и скорость приняты за основные, то, комбинируя их, будем стремиться получить размерности L , F и Т.
Найдем размерность длины
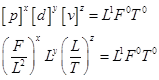
откуда 
Следовательно, 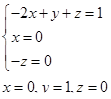
.
Таким образом, для получения размерности длины нужно принять следующую комбинацию р, d и v :
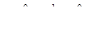 .
.
Найдем размерность силы:
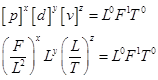 ,
,
откуда

Следовательно,
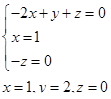 ;
;
т. е. для получения размерности силы нужно воспользоваться следующей комбинацией 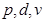 :
:
 .
.
Найдем размерность времени
 ,
,
откуда
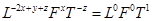
Следовательно,
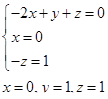 .
.
Размерность времени получим из приводимой ниже комбинации р, d и v :
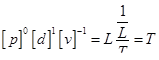
В каждом варианте комбинации этих величин выбираются так, чтобы в результате можно было бы получить безразмерный параметр. Теперь для каждого из двух вариантов выведем безразмерные параметры.
Вариант 1. Комбинации трех величин, принятых при выводе безразмерных параметров 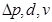 , должны быть выбраны так, чтобы можно было получить размерности остальных величин, а затем в результате деления привести полученную величину к безразмерному виду.
, должны быть выбраны так, чтобы можно было получить размерности остальных величин, а затем в результате деления привести полученную величину к безразмерному виду.
Для величины 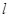 можем записать:
можем записать:

Отсюда

или

Для g имеет место соотношение
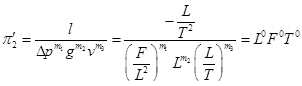
Отсюда система уравнений
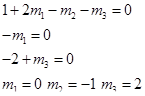
Тогда безразмерный параметр имеет вид Fr
 .
.
Аналогично для ρ получим
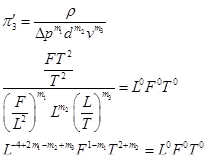
Откуда можно записать систему уравнений

Третий безразмерный параметр имеет вид

Безразмерный параметр для η имеет вид

Откуда можно записать систему уравнений
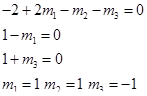
или безразмерный параметр имеет вид

Безразмерный параметр для τ0 имеет вид

Откуда можно записать систему уравнений
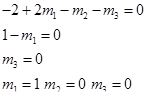
или безразмерный параметр имеет вид

| Таким образом, получим пятый безразмерный параметр в виде |
|
|
Эти критерии используются для описания стационарного движения вязко-пластических жидкостей Eu, Fr, La' и La".
Аналогично, если вывести безразмерные параметры для 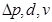 , то получим
, то получим
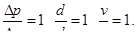
Ввиду того, что из восьми величин, входящих в уравнение, три приняты за независимые переменные, число безразмерных параметров уменьшится на число независимых переменных, т. е. получим п — т = 8—3 = 5 безразмерных параметров.
Вариант 2. Принимая размерные величины 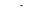 за основные и выводя из
за основные и выводя из 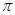 -теоремы безразмерные параметры, получаем следующие выражения:
-теоремы безразмерные параметры, получаем следующие выражения:

Сопоставим их с параметрами варианта I:
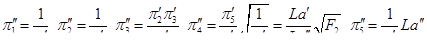
Ввиду того, что искомая величина 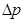 входит входит в параметр Eu, то результаты опытов представлены в виде
входит входит в параметр Eu, то результаты опытов представлены в виде

Так как величина 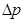 входит в параметр Eu, остальные три параметра выбираем так, чтобы там искомая величина
входит в параметр Eu, остальные три параметра выбираем так, чтобы там искомая величина 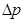 не участвовала.
не участвовала.
Уравнение можно выразить и с помощью параметра Лагранжа, в котором участвует 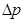 , т. е.
, т. е.

Это уравнение применимо для стационарного движения; если же движение нестационарное, необходимо принять во внимание и параметр Струхаля.
При горизонтальном положении трубы силы тяжести не оказывают влияния на движение, поэтому g во внимание не принимается.
Так как при изотермическом движении физические свойства жидкости по длине трубы не меняются, расход и сечение остаются постоянными, то потери давления, приходящиеся на единицу длины (из уравнения неразрывности), бывают разными. В этом случае характерным является 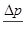 . Например, если будем знать потери давления, соответствующие 100 м длины, то можно определить потери давления на 200, 300 м и т. д. Здесь начальные и концевые участки во внимание не принимаются. Тогда перепад давления па единицу длины может быть выражен как
. Например, если будем знать потери давления, соответствующие 100 м длины, то можно определить потери давления на 200, 300 м и т. д. Здесь начальные и концевые участки во внимание не принимаются. Тогда перепад давления па единицу длины может быть выражен как
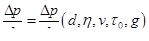 .
.
Так как определяется 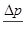 , то параметр
, то параметр 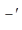 отпадает и параметр Эйлера записывается в виде
отпадает и параметр Эйлера записывается в виде
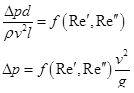
Для вязких жидкостей аналогичное уравнение, выведенное независимо друг от друга Дарси и Вейсбахом, называется уравнением Дарси — Вейсбаха.
Таким образом,
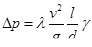
где 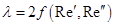 — коэффициент гидравлических сопротивлений.
— коэффициент гидравлических сопротивлений.
Рассмотрим уравнение длинной двухпроводной линии [9]. Двухпроводная линия представлена системой с равномерно распределенными утечками, индуктивностями, сопротивлениями и емкостями. Разность потенциалов U и сил тока i в сечениях х и 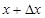 определяется на основании закона Кирхгофа, записанного для процесса, протекающего на отрезке
определяется на основании закона Кирхгофа, записанного для процесса, протекающего на отрезке 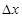 в промежуток времени
в промежуток времени 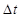 . Разность U ( x , t ) - U (х + Ах, t ) определяет разность потенциалов на индуктивностях и омических сопротивлениях
. Разность U ( x , t ) - U (х + Ах, t ) определяет разность потенциалов на индуктивностях и омических сопротивлениях
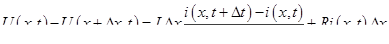
где L и R — соответственно индуктивность и омическое сопротивление на единицу длины.
Первый член правой части, характеризующий изменение э. д. с. на индуктивностях, определяется изменением силы тока во времени. Второй член — разность потенциалов, которая рассчитывается по закону Ома.
Второе уравнение — баланс силы тока, определяемый конденсатором и утечкой, т. е.
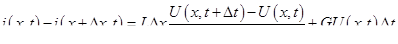
где С — емкость, приходящаяся на единицу длины; G- — проводимость на единицу длины.
Первый член правой части — сила тока, проходящего через конденсатор и характеризуемого изменением в течение времени разностью потенциалов. Второй член — сила тока — утечка, определяемая по закону Ома.
Приведенные два уравнения — конечно-разностные уравнения длинной двухпроводной линии. Переходя к пределу при  , можно получить:
, можно получить:
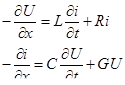
Эта система уравнения при G = 0 вполне аналогична дифференциальным уравнениям движения капельной жидкости в трубопроводе при  .
.
Рассмотрим неустановившееся движение реальной среды в горизонтальной круглой цилиндрической трубе. В этом случае одно время релаксации характеризует нестационарность вдоль оси, другое — вдоль сечения. Предполагается, что второе пренебрежимо мало по сравнению с первым. Поэтому исследуется нестационарность, развивающаяся вдоль оси трубы, т. е. рассматривается квазиодномерное движение, характеризуемое параметрами, осредненными по сечению. Предполагается, что жидкость малосжимаемая, т. е. изменение ее скорости вдоль оси мало. В сечении 1—1 (см. Рис. 9) среднее давление обозначается через р (х, t ), а в сечении 2—2 — через  .
.
Касательное напряжение обозначается через 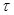 . Тогда сила трения, действующая на боковую поверхность элементарного круглого цилиндра, будет
. Тогда сила трения, действующая на боковую поверхность элементарного круглого цилиндра, будет  , где S 1 — смоченный периметр.
, где S 1 — смоченный периметр.
В уравнении движения «местная скорость» приближенно заменяется средней по сечению скоростью v , но это не влияет на конечный результат.
Сумма сил сопротивления и давления равна 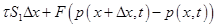 , где F — площадь поперечного сечения.
, где F — площадь поперечного сечения.
Переходя к пределу, получаем

Абсолютную величину силы инерции выразим через 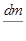 , где
, где
|
|
 — масса среды в отсеке 1—1, 2—2 трубы. Тогда в пределе.
— масса среды в отсеке 1—1, 2—2 трубы. Тогда в пределе.
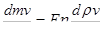
На основании принципа Д'Аламбера
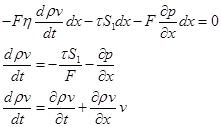
Ввиду того, что скорость мало изменяется по длине трубы, вторим членом этого равенства но сравнению с первым можно пренебречь, т.е. 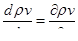
Сформулируем более полно условия, при которых можно пренебречь вторым членом но сравнению с первым. Первый член 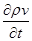 имеет порядок
имеет порядок  , второй
, второй 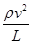 ( L — характерный размер, в данном случае длина трубопровода, Т — характерное время, в качестве которого может быть принято время релаксации). Вторым членом можно пренебречь по сравнению с первым при условии
( L — характерный размер, в данном случае длина трубопровода, Т — характерное время, в качестве которого может быть принято время релаксации). Вторым членом можно пренебречь по сравнению с первым при условии
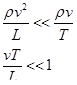
Параметр 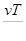 безразмерный. Оценим величину этого параметра для магистрального трубопровода:
безразмерный. Оценим величину этого параметра для магистрального трубопровода: 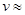 1 м/сек;
1 м/сек;  100 км.
100 км.
Если принять, что время релаксации порядка нескольких часов соответствует времени практического достижения стационарного
режима, то получим 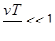 . Тогда
. Тогда

где R гидравлический радиус
Для изотермического движения принимается уравнение состояния
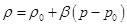
Отсюда
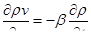
Вводя вместо 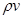 среднемассовую скорость w, можно записать
среднемассовую скорость w, можно записать
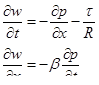
Из анализа размерностей нетрудно установить, что при ламинарном режиме 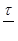 пропорционально средней скорости в первой степени,
пропорционально средней скорости в первой степени,
а при турбулентном режиме — квадрату скорости.
Необходимо еще раз отметить, что здесь мы воспользовались принципом квазистационарности, т. е. силы сопротивления определяли по формулам для стационарного режима. Принимая  , находим
, находим
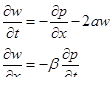
где 2а — коэффициент сопротивления.
Преобразуем систему к одномерному уравнению

Рассмотрим, как, используя соображения размерности, можно упростить уравнение. Если использовать безразмерные переменные, получим :
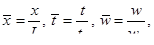
где L , t 0 и w 0 — характерные величины.
В качестве L принималась длина трубопровода. Следовательно, в
безразмерных переменных

Из условия 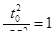 определяется
определяется  . Окончательно
. Окончательно

Если коэффициент при члене 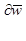 достаточно большой, то можно пренебречь силой инерции
достаточно большой, то можно пренебречь силой инерции 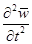 по сравнению с силой сопротивления
по сравнению с силой сопротивления 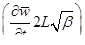 .
.
Таким образом, перепад давления расходуется только лишь на преодоление сил сопротивления. В этом случае уравнение принимает вид

Естественно, что принятое предположение оправдывается для трубопроводов очень большой длины и при движении в них жидкости очень большой вязкости. При определении пускового давления в трубопроводах и в скважине можно пренебречь силой инерции
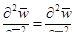
Уровень, который может быть принят как достаточно большой, определяется на основании сопоставимых расчетов. Соображения подобия позволяют, не решая уравнения, получить некоторую информацию. Например, второй закон Ньютона для частного случая потенциального силового поля [2] можно записать в виде
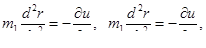
приняв 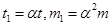 , можно получить
, можно получить 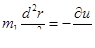
Следовательно, если уменьшить массу точки в 25 раз, то на прохождение орбиты потребуется времени в пять раз меньше.
3. МЕХАНИЧЕСКИЕ МОДЕЛИ
Механические свойства различных материалов могут быть описаны разными теоретическими схемами. Такие схемы позволяют давать качественные описания процесса деформации. Для построения замкнутой теории движения среды должна быть известна связь между кинематическим и динамическим состояниями частицы, в частности между напряжениями и деформациями, выражаемая при помощи механического уравнения состояния тела.
К простым средам относятся следующие тела: упругое, вязкое, жестко-пластическое. Механическое уравнение состояния упругого тела выражается при помощи закона Гука, который для одноосного напряженного состояния имеет вид:
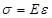 , (I.83)
, (I.83)
где  — напряжение; Е — модуль Юнга;
— напряжение; Е — модуль Юнга; 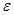 — относительная деформация.
— относительная деформация.
Механическое уравнение состояния упругого тела изображается в виде механической модели, представляющей собой пружину (рис. 11).
Механическое уравнение состояния вязкого тела для одноосного напряженного состояния выражается при помощи закона Ньютона
 . (1-84)
. (1-84)
где 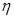 — вязкость;
— вязкость;  - — скорость деформации.
- — скорость деформации.
Вязкое тело изображается моделью, состоящей из поршня, двигающегося в цилиндре с вязкой жидкостью (рис. 12).
Жестко-пластическое тело при напряжениях ниже предела текучести ат не деформируется. В таком теле течение развивается лишь при напряжениях, удовлетворяющих условию текучести  . Модель такой среды может быть изображена в виде площадки с кулоновым трением (рис. 13).
. Модель такой среды может быть изображена в виде площадки с кулоновым трением (рис. 13).
Выше были приведены три простейшие механические модели, иллюстрирующие механические уравнения состояния вязкого, упругого и жестко-пластического тела. Комбинируя эти простые модели,
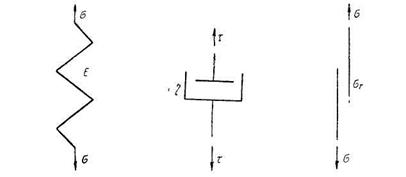
Рис. 11. . Рис. 12. Рис. 13.
можно рассматривать различные сложные среды. Так, упруго-пластическую среду можно характеризовать моделью, в которой
|
|
последовательно соединены упругий и пластический элементы (рис. 14).
Упруго-вязкая среда Фойхта характеризуется моделью, в которой параллельно соединены упругий и вязкий элементы (рис. 15).

Рис. 14. Рис. 15. Рис. 16.
Для такой среды полное напряжение будет складываться из напряжения, соответствующего упругой деформации, и напряжения, вызываемого вязким сопротивлением,
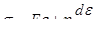 . (1.85)
. (1.85)
В состоянии покоя, т. е. при 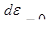 , такая среда ведет себя как упругая. При
, такая среда ведет себя как упругая. При  в среде возникает постоянное напряжение
в среде возникает постоянное напряжение 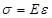 . Если при t = 0,
. Если при t = 0, 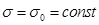 , то из (1.85) получим
, то из (1.85) получим
 . (1.86)
. (1.86)
|
|
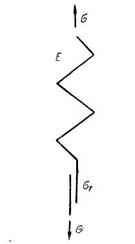
Рассмотрим теперь среду, которой соответствует модель, состоящая из последовательно соединенных упругого и вязкого элементов (рис. 16). Для такой среды Максвеллом, получен следующий закон деформации:
 (1.87)
(1.87)
где  скорость деформации;
скорость деформации; 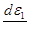 - скорость упругой деформации;
- скорость упругой деформации;
 -скорость вязкой деформации.
-скорость вязкой деформации.
Из закона Гука дифференцированием определим
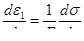 (1.88)
(1.88)
Определив  - из закона Ньютона (1.84) и подставив полученные значения
- из закона Ньютона (1.84) и подставив полученные значения 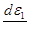 из (1.88) и (1.87), получим
из (1.88) и (1.87), получим
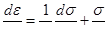 (1.89)
(1.89)
Если 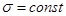 , то тело, описываемое уравнением (1.89), будет деформироваться с постоянной скоростью, т. е. течь подобно вязкой жидкости.
, то тело, описываемое уравнением (1.89), будет деформироваться с постоянной скоростью, т. е. течь подобно вязкой жидкости.
Теперь рассмотрим другой случай. Пусть в момент времени t = 0 на тело действует напряжение  и соответствующее начальное
и соответствующее начальное
относительное удлинение, равное 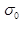 . Положим
. Положим 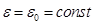 , что достигается, в частности, закреплением концов стержня. В этом случае
, что достигается, в частности, закреплением концов стержня. В этом случае 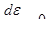 и из уравнения (1.89)
и из уравнения (1.89)
 (1.90)
(1.90)
где  время релаксации
время релаксации
Из (1.90) видно, что напряжение со временем изменяется и no-закону экспоненты при 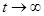
 стремится к нулю (рис. 17). Уравнение Максвелла с качественной стороны описывает так называемую релаксацию напряжения, т. е. ослабление со временем напряженного состояния при неизменной деформации. В дальнейшем уравнение Максвелла будет нами использовано для конкретного объяснения явления вытекания глин в скважину в процессе проводки скважины и дальнейшей ее эксплуатации. Находясь под нагрузкой, твердые тела (в частности, цементный камень) медленно деформируются. С повышением температуры это явление текучести тел резко возрастает.
стремится к нулю (рис. 17). Уравнение Максвелла с качественной стороны описывает так называемую релаксацию напряжения, т. е. ослабление со временем напряженного состояния при неизменной деформации. В дальнейшем уравнение Максвелла будет нами использовано для конкретного объяснения явления вытекания глин в скважину в процессе проводки скважины и дальнейшей ее эксплуатации. Находясь под нагрузкой, твердые тела (в частности, цементный камень) медленно деформируются. С повышением температуры это явление текучести тел резко возрастает.
Текучесть твердых тел при высоких температурах обладает рядом характерных свойств и называется ползучестью, или крипом. Изучение ползучести твердых тел проводится опытным путем — растяжением стержней при постоянной температуре и фиксированных нагрузках.
Отложим на оси ординат относительное удлинение, а на оси абсцисс — общее время испытания t , тогда кривая длительных испытаний будет иметь вид, показанный на рис. 48. Отрезок ОА соответствует начальной деформации 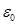 , полученной стержнем при его
, полученной стержнем при его
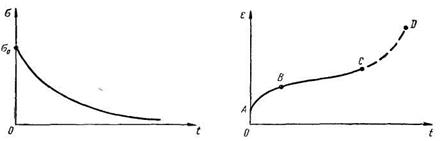
Рис. 17. Рис.18.
нагружении. Отрезок АВ характеризует убывание скорости ползучести. С приближением к точке В уменьшение скорости деформации замедляется, и на участке ВС, называемом вторым периодом ползучести, скорость деформации практически становится постоянной. Указанный период, характеризуемый минимальной скоростью ползучести, бывает обычно наиболее длительным и заканчивается разрушением тела.
Вязко-пластическое тело изображается моделью, которая состоит из вязкого элемента и площадки с кулоновым трением, соединенных параллельно (рис. 19). Уравнение деформации вязко-пластического тела Шведова — Бингама имеет следующий вид:
 при
при  ,
,
где 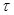 — предельное напряжение сдвига.
— предельное напряжение сдвига.
При  то тело не деформируется. Из рис. 20 видно, что для ряда тел течение наступает только после определенной нагрузки, при этом скорость течения зависит от вязкости среды.
то тело не деформируется. Из рис. 20 видно, что для ряда тел течение наступает только после определенной нагрузки, при этом скорость течения зависит от вязкости среды.
Для выражения механических свойств высокополимеров необходимо привлекать модели, состоящие из многих элементов. Обычно для таких моделей характерно большое число параметров. Авторы рассматривали двухпараметрические модели  .
.
Рассмотрим модель (рис. 21), содержащую три параметра Е1, Е2, 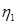 . Для такой среды закон деформации можно получить следующим образом.
. Для такой среды закон деформации можно получить следующим образом.
|
|
|
|
Рис.19. Рис.20.
Напишем закон деформации для простых элементов I, II, III:

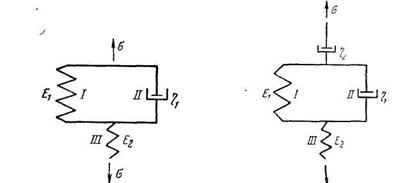
Рис. 21. Рис. 22.
а также для условий равновесия и неразрывности

Аналогично можно привести модель с четырьмя параметрами  (Рис. 22).
(Рис. 22).
4. Уравнения состояния и законы переноса
Для описания состояний макрофизических свойств тел и переноса процесса взаимодействия применяется понятие обобщенного заряда — объем, масса и т. д. Величина заряда в теле определяет его состояние, а перенос его количественно характеризует процесс взаимодействия.
Величина заряда относится к экстенсивным величинам, т. е. к величинам, распределенным по объему. Заряд может переноситься под действием обобщенного потенциала — интенсивной величины, т. е. величины, распределенной по поверхности. К обобщенным потенциалам относятся температура, давление, электрический потенциал, напряжение и т. д.
Законы переноса определяют зависимость между потоками заряда и разностью потенциалов. Закон же состояния определяет зависимость между потенциалом и зарядом. Так, например, для жидких, газообразных и твердых однородных тел заряд — это объем, обобщенные потенциалы — давление и температура, уравнение состояния — зависимость, выражающая связь между объемом, давлением и температурой. Зависимость между напряжениями и деформациями — это механическое уравнение состояния.
Если поток заряда переносится в пространстве в одном направлении, то такой перенос называется одномерным, в случае же переноса в двух направлениях — плоским, а в трех направлениях — пространственным.
Наибольшее распространение получило уравнение Менделеева — Клайперона ( pV = zRT , где р — давление, V — объем, R — газовая постоянная, Т — температура, К, z — коэффициент сжимаемости).
Безразмерный коэффициент сжимаемости зависит от безразмерного давления  и безразмерной температуры
и безразмерной температуры 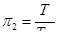 (ркр и Ткр — соответственно критическое давление и температура).
(ркр и Ткр — соответственно критическое давление и температура).
Для нефтепромысловой практики, учитывая точность расчетов, определяемую допусками, точностью исходной информации, а также точностью контрольно-измерительных приборов, коэффициент z можно принять равным единице, т. е. газ принимается идеальным. Так, например, для контроля давления наиболее совершенное средство — образцовые манометры, погрешность которых для некоторых манометров и интервалов давлений составляет +0,35% максимального давления. Если при трубопроводном транспорте газа давление в начале трубопровода близко 100 кГ/см2, то применяется манометр со шкалой 100 кГ/см2, причем погрешность будет 0,35 кГ/см2. Учет коэффициента z при сравнительно небольшой протяженности газопровода внесет уточнение не более указанной погрешности.
Приведем пример, не имеющий прямого отношения к излагаемому, по хорошо иллюстрирующий отмеченное положение. При трубопроводном транспорте воды, учитывая допуски, точность расходомеров, погрешность в определении гидравлических сопротивлений также может достигнуть нескольких процентов. Часто в инженерных исследованиях это не учитывается. Например, точность рассчитанных величин не адекватна точности контрольно-измерительных приборов. Иногда составляют эмпирические уравнения, в которых влияние отдельных факторов меньше, чем точность, с которой может быть определена функция. Придавая большое значение этому вопросу, авторы посвятили специальный параграф краткому изложению теории ошибок, в основном имея в виду их прикладное значение для нефтепромысловой механики.
Приведем уравнение состояния жидкости, которое часто применяется в нефтегазопромысловой механике для баротропной жидкости,
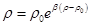
где  — плотность при давлении р0;
— плотность при давлении р0; 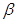 — коэффициент объемного упругого расширения жидкости.
— коэффициент объемного упругого расширения жидкости.
Данное уравнение может быть аппроксимировано линейной зависимостью
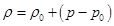
Отмеченное справедливо для так называемых малосжимаемых жидкостей. Очень часто, идеализируя уравнение, не указывают условия, при которых эта идеализация практически приемлема.
Так, в рассматриваемом случае только по коэффициенту упругого расширения жидкости не могут быть отнесены к малосжимаемым. Это зависит и от интервала изменения давления, т. е. если имеются две жидкости и у одной коэффициент 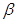 меньше, чем у другой, это не свидетельствует о возможности применения линейной аппроксимации. Необходимо обратить внимание на интервал изменения давления.
меньше, чем у другой, это не свидетельствует о возможности применения линейной аппроксимации. Необходимо обратить внимание на интервал изменения давления.
Рассмотрим критерии, которые позволяют выяснить условия, при которых следует учитывать упругость и сжимаемость жидкости. Так, например, при нестационарном движении вязкой жидкости в длинном трубопроводе, а также в пористой среде целесообразно применить понятие времени релаксации (ослабление состояния тела после прекращения воздействия, вызвавшего это состояние). Оценим порядок времени релаксации для движения в трубопроводе. Под порядком понимается порядок величины: секунды, десятки секунд, сотни секунд и т. д. Время релаксации будет зависеть от силы инерции, определяемой массой (плотностью) и вязкостью. Так как развитие профиля скоростей зависит в основном от радиуса, следовательно,
 .
.
Нетрудно видеть, что из этих четырех величин может быть составлен один безразмерный параметр.
Приведенная зависимость представляется в виде степенной комбинации, что возможно при одном безразмерном параметре
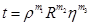 .
.
Пользуясь размерностью величин, входящих в последнее уравнение, получаем
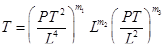
где Т, Р и L — соответственно размерности времени, силы и длины. В левой и правой части уравнения размерности должны быть одинаковые (однородность размерности). В левой части не имеется Р и L , точнее, они входят в нулевой степени. Следовательно, и в правой части Р и L должны быть в нулевой степени, Т — в первой, т. е.
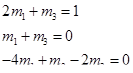 .
.
Отсюда т1 = 1; m 3 = —1; m2 = 2. Таким образом,
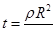
Время релаксации имеет порядок 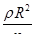
Приведем численный пример. Через 4 сек трубопровод прокачивается вязкая нефть плотностью 0,8 и вязкостью 5 спз. Тогда
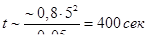
Таким образом, время релаксации порядка нескольких минут.
Если рабочий период трубопровода больше времени релаксации, то можно пренебречь упругостью жидкости и рассматривать движение как стационарное. При исследовании пускового периода трубопровода, время которого соизмеримо со временем релаксации, необходимо рассматривать нестационарное движение.
Для твердого скелета упругой пористой среды принимается следующее уравнение состояния:
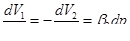
где 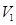 — объем норового пространства;
— объем норового пространства; 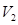 — объем жидкости; V — начальный объем;
— объем жидкости; V — начальный объем;  — коэффициент сжимаемости.
— коэффициент сжимаемости.
Строго говоря,  не коэффициент сжимаемости, так как в приведенную формулу входит изменение порового пространства, а изменение объема твердого скелета. Экспериментальные же исследования показывают, что эти величины мало отличаются.
не коэффициент сжимаемости, так как в приведенную формулу входит изменение порового пространства, а изменение объема твердого скелета. Экспериментальные же исследования показывают, что эти величины мало отличаются.
Перейдем к рассмотрению различных уравнений переноса массы (закон Дарси и Фика), тепла (закон Фурье), электрического тока (закон Ома). Подробно изложим, как экспериментальным путем установлен закон переноса массы в пористой среде — закон Дарси. Рассмотрим движение практически несжимаемой жидкости. Введем понятие фиктивной средней скорости, т. е. когда поток жидкости «размазывается» по всему сечению твердого скелета и пор. Скорости и ускорения изменяются как по величине, так и по направлению пористой среды. Ввиду большого разнообразия пор невозможно учесть скорость отдельных частиц. Принято рассматривать значения скоростей ъ некотором объеме. Практическая несжимаемость жидкости проверяется равенством расходов при входе и выходе, при этом имеется в виду равенство в пределах погрешности применяемых расходомеров. Таким образом, в данном случае заряд может быть охарактеризован
|
|
|
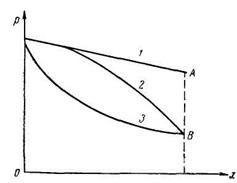
Процесс фильтрации несжимаемой жидкости характеризуется прямой линией 1. Сравним случаи фильтрации сжимаемой и несжимаемой жидкостей (сравниваются жидкости, имеющие одинаковые плотности при одинаковых объемных расходах и давлениях на входе). Объемный расход по мере удаления от начала отсчета растет для сжимаемой жидкости, в результате чего давление в конце отсчета (точка В) ниже давления несжимаемой жидкости (точка А).
Рассмотрим, по какой из кривых (2 или 3) должно произойти изменение давления. По мере удаления от начала отсчета перепад давления должен увеличиваться ввиду непрерывного увеличения расхода (кривая 2). По кривой 3 интенсивность перепада давления уменьшается.
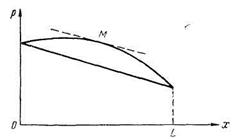
Для большей физической ясности рассмотрим другой пример, когда давление в начале и в конце отсчета для сжимаемой и несжимаемой жидкостей одинаково. По мере удаления от начала отсчета расход для сжимаемой жидкости будет расти, оставаясь меньше, чем для несжимаемой. В некоторой точке М (рис. 24) расходы несжимаемой и сжимаемой жидкостей будут одинаковы, после которой расход для сжимаемой жидкости будет больше, чем для несжимаемой. До точки М интенсивность изменения давления для сжимаемой ншдкости будет больше, чем для несжимаемой, в точке М они равны, а затем интенсивность изменения давления сжимаемой жидкости будет меньше интенсивности несжимаемой. Так как интенсивность изменения давления характеризуется производной, то в точке М касательная, проведенная к кривой, будет параллельна прямой, проведенной для сжимаемой жидкости.
Следовательно (см. рис. 23), при движении сжимаемой жидкости кривая распределения давлений обращена вогнутостью к оси абсцисс. Это относится к стационарной фильтрации, когда величины, характеризующие фильтрацию, практически неизменны во времени.
|
|
Состояние систем термодинамики характеризуется обобщенным зарядом. Если заряд находится в статическом состоянии и не изменяется во
Рис. 24.
времени, то система является стационарной, равновесной (статика). Пронизывание системы неизменным зарядом соответствует стационарно неравновесной системе (кинетика). При изменяющемся заряде, но не пронизывающем систему, система нестационарно равновесна стато-динамика;. и, наконец, для нестационарно неравновесной системы (кинето-динамика) происходит перенос заряда и одновременное изменение во времени.
Так как будем рассматривать безынерционную фильтрацию, то плотность не характеризует данный процесс. Следовательно, скорость фильтрации w определяется следующей функциональной зависимостью:
 б
б
где di — диаметры зерен, составляющих пористую среду. На основании π-теоремы можно записать
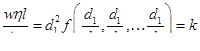
Стоящая в правой части величина к, характеризующая пористую среду и зависящая от ее состава, называется проницаемостью. Она имеет размерность квадрата длины и определяется опытным путем. На первый взгляд, приведенный закон переноса (закон Дарси) установлен лишь только на основе применения 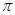 -теоремы. Но это не так.
-теоремы. Но это не так. 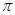 -теорема позволяет лишь экономно познать процесс. В данном случае безынерционность движения проверяется экспериментально на основе того, что зависимость между w и
-теорема позволяет лишь экономно познать процесс. В данном случае безынерционность движения проверяется экспериментально на основе того, что зависимость между w и 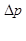 прямолинейная.
прямолинейная.
В дифференциальной форме закон Дарси может быть записан в виде
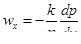 .
.
В этом случае рассматривается одномерное движение вдоль оси х. Вдоль оси давление уменьшается и 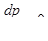 . В правой части поставлен
. В правой части поставлен
знак минус, так как скорость фильтрации, направленная вдоль оси х, положительна.
Для пространственной фильтрации в изотропной пористой среде:
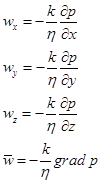 .
.
Закон Дарси может быть истолкован как линейный закон сопротивления в уравнениях движения. При исследовании стационарных движений применяется закон сопротивления, полученный для стационарных движений, т. е. применяется принцип квазистационарности. Отмеченное, вероятно, справедливо для процессов, протекающих во времени сравнительно медленно.
Время релаксации нестационарных процессов, происходящих в пористой среде в результате сжимаемости жидкости и скелета, характеризуется коэффициентом пьезопроводности 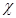 , имеющим размерность см2/сек,
, имеющим размерность см2/сек,
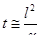
где 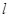 — характерный размер.
— характерный размер.
Так, для одной скважины, расположенной в пласте, на котором скважины размещены по 200-метровой сетке I может быть принято равным половине расстояния между скважинами, т. е. 100 м.
Для пласта проницаемостью 0,25 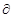 , при коэффициенте упругой емкости
, при коэффициенте упругой емкости 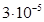 и фильтрации жидкости вязкостью 7,5 спа
и фильтрации жидкости вязкостью 7,5 спа 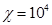 см2/сек.
см2/сек.
Тогда
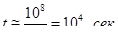
Таким образом, время релаксации будет около 3 ч,
т. е. нестационарность представляет интерес для кратковременного исследования скважин, т. е. таких исследований, время которых равно нескольким часам. Для разработки пластов, когда время исчисляется годами, нестационарность в этом случае можно не учитывать.
Для больших 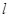 , характеризующих размер пласта, например 10 км,
, характеризующих размер пласта, например 10 км,
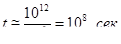
т. е. время релаксации будет около 3 лет. Для разработки такой сравнительно крупной залежи нестационарность необходимо учитывать.
Отмеченное относится и к случаям приложения нагрузок статической и динамической, для которых напряжение зависит не только от упругой деформации, но и от ее скорости. Динамические расчеты с учетом неравновесности процесса представляют большой интерес для нефтепромысловой механики, особенно для новых методов воздействия на пласт. Тем не менее они не получили должного развития, поэтому в данной книге мы рассмотрим их кратко. Заметим, что для тиксотропных, изменяющихся во времени глинистых и цементных растворов, принцип квазистационарности не применим для расчета нестационарного движения в трубах. Закон Дарси справедлив в области линейной фильтрации.
Для нелинейной фильтрации находят применение степенные законы. Обычно степенные законы записываются для одномерных случаев. Представляет некоторый интерес рассмотрение обобщения и для пространственной фильтрации. Для одномерного случая
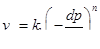 .
.
Проверим, можно ли для двухмерного случая применить аналогичные выражения
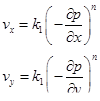 .
.
Нетрудно показать, что приведенное уравнение неинвариантно относительно поворота осей координат. При повороте координатных осей координаты и проекции скоростей на соответствующей оси меняются следующим образом:
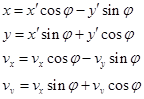 (1.91)
(1.91)
Легко заметить, что проекции градиента давления на оси х и у
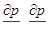 определяются по тем же формулам:
определяются по тем же формулам:
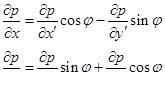
где  и проекции градиента давления на оси х' и у'. Тогда
и проекции градиента давления на оси х' и у'. Тогда
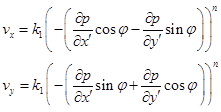 (1.92)
(1.92)
Сравнивая (1.91) с (1.92), нетрудно показать, что выполнение
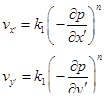
возможно лишь при п = 1.
Следовательно, записанный нелинейный закон фильтрации неинвариантен относительно поворота осей координат.
Покажем, что одной из возможных записей нелинейного закона фильтрации, обеспечивающей инвариантность относительно поворота осей координат, является следующая.
Пусть

Тогда проводя несложные преобразования получим

модуль градиента инвариантен относительно поворота осей координат. Проекций скорости в этом случае имеют вид :
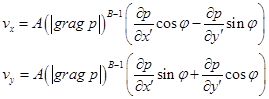
Естественно, что уравнение неразрывности, инвариантное относительно поворота осей координат, не изменяется при подстановке инвариантных величин vх и vy .
Следовательно,
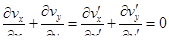
Или

В случае однопараметрической модели обобщение на пространственный случай проводится сравнительно просто, как было показано ниже. Если модель двухпараметрическая, например вязко-пластическая, т. е. характеризуется вязкостью и пластичностью — предельном напряжением сдвига, то на основании простейших одномерных течении нельзя описать уравнение для пространственного случая без применения той или иной гипотезы, которая в дальнейшем проверяется экспериментально. Так, для одномерного течения
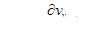
Рассмотрим возможные пути обобщения приведенного закона, когда осевая скорость есть функция двух переменных v = vx (х, у), т е. происходит движение в некруглой трубе. В этом случае имеют место два касательных напряжения  . Самое простое обобщение
. Самое простое обобщение

Покажем на одном частном примере несостоятельность такого обобщения. Рассмотрим движение в круглой цилиндрической трубе.
Для одномерного случая имеем одно касательное напряжение 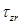 , направленное вдоль поверхности и зависящее ввиду симметрии только от
, направленное вдоль поверхности и зависящее ввиду симметрии только от  ,
,
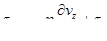
Из приведенных  невозможно получить формулу для
невозможно получить формулу для 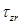 . Для возможности отмеченного перехода в общем случае перед
. Для возможности отмеченного перехода в общем случае перед 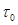 ставится коэффициент
ставится коэффициент
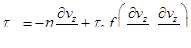 .
.
Где ,например
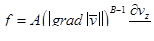
Это выражение инвариантно относительно поворота осей координат. При п = 2 получается обобщение в форме Генки — Ильюшина.
Как было отмечено, диффузионные процессы представляют большой интерес для нефтепромысловой механики. Приведем некоторые задачи, которые описываются диффузионной моделью. Это в первую очередь смешивающиеся вытеснения, которые могут быть как при использовании растворителей для увеличения нефтеотдачи, так и в случае вытеснения глинистого раствора цементным при цементировании скважин.
Диффузионные процессы происходят и в стволе газовой скважины при ее остановке. Их учет необходим для исследования сепарации газоконденсатных систем в трапах. Приведем один процесс, происходящий в глинистых пластах, для которых диффузия является определяющей. Известно, что глина имеет очень маленькую проницаемость и практически считается непроницаемой, т. е. исключается из рассмотрения как при подсчете запасов газа, так и при разработке. Ниже покажем, что диффузионный перенос газа в глинах и глинистых пластах довольно значителен. Феноменологически диффузия описывается законом Фика:
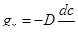
где gx — проекция на ось х скорости переноса; с — концентрация D — коэффициент диффузии.
По аналогии с законом Дарси можно записать
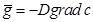
Коэффициент диффузии имеет размерность см2/сек. Нетрудно показать из анализа размерности, как это делается при определении порядка времени релаксации, что порядок диффузионного времени определяется так:
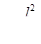
где 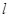 — характерный размер.
— характерный размер.
Коэффициент диффузии в пористых средах составляет 10~5 см2 /сек» Для глинистого пропластка толщиной 10 см
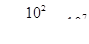 сек
сек
т.е. диффузионное время составляет 100 суток.
Для пропластка толщиной 1 см это время будет составлять одни сутки.
Таким образом, прослойки глины могут представлять опасность как источник газопроявления при проводке скважин. Кроме того, их необходимо учитывать при подсчете запасов и анализе разработки линеаризованных газовых и газоконденсатных пластов
Явление переноса тепла отмечается во всех звеньях бурения, нефтедобычи и транспорта и описывается законом Фурье
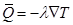
где Q — плотность теплового потока;  — коэффициент теплопроводности; Т — температура.
— коэффициент теплопроводности; Т — температура.
Это уравнение, как и все приведенные выше, относится к однородной и изотропной средам, для которых коэффициенты проницаемости, диффузии и теплопроводности одинаковы во всех направлениях (изотропность) и во всех точках (однородность).
Для нефтепромысловой механики представляет большой интерес и закон переноса электрического тока как для расчета некоторых процессов, например электрокаротажа, электроподогревателей и т.д. , так и в основном для метода электрических аналогий. Закон переноса электрического тока — закон Ома — имеет вид
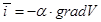 ,
,
где  — плотность электрического тока;
— плотность электрического тока; 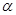 — коэффициент пропорциональной электропроводности; V — потенциал.
— коэффициент пропорциональной электропроводности; V — потенциал.
В приведенной ниже таблице нетрудно заметить аналогию между законами Дарси, Фика, Фурье и Ома.
2.4.Метод аналогий.
Среди различных явлений, встречаемых в природе, выявлено много математических аналогий. За последние десятилетия в практике применяются лабораторные исследования и проекты, основанные на электрических, магнитных, электродинамических, электромагнитных, тепловых, звуковых, оптико-механических, магнитно-оптических и других аналогиях и на теории моделирования. Электромоделирование различных физических явлений широко используется в теории фильтрации, гидравлике, гидродинамике, строительстве, теплотехнике, теории упругости, механике грунтов, теории механизмов, акустике, теории автоматического регулирования, а также в других областях науки и техники.
В современном гидротехническом строительстве при строительстве больших и сложных гидротехнических объектов требуется проводить сложные исследования по фильтрации. Теоретическое исследование этих вопросов очень сложно, а иногда и неразрешимо. Эти сложные вопросы очень легко разрешаются с помощью метода ЭГДА (электрогидродинамическая аналогия), в том числе разрешаются многие задачи, относящиеся к фильтрации нефти, газа и газированных жидкостей.
Применение метода ЭГДА при исследовании фильтрации почвенных вод под гидротехнические сооружения впервые в 1918 г. было предложено и теоретически обосновано академиком Н. Н. Павловским. Метод ЭГДА также широко используется в различных областях научных исследований.
Применение центробежного моделирования дает хорошие результаты при решении следующих задач, относящихся к статике и динамике пород: определение прочности земляных строительных откосов; определение прочности валов и других строительных фундаментов; распределение напряжений в породах и на контакте строительных поверхностей с породой; оседание зданий; фильтрация воды в породе и влияние фильтрации па породы; определение в связанных породах сил трения и сцепления и т. д. Ниже покажем два простых примера, относящихся к аналогии.
Аналогия между электрическими и механическими явлениями
В замкнутую цепь (рис. 25) включены конденсатор с емкостью С, омическое сопротивление R, катушка самоиндукции L и ключ К.
Через цепь проходит электрический ток I. Для последовательной цепи, как известно из закона Кирхгофа, разность потенциалов будет состоять из суммы разности напряжений на
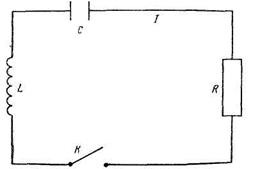
Рис.25
омическом сопротивлении, конденсаторе и катушке. Эти три составляющие рассчитываются следующим образом:
а) в результате самоиндукции разность напряжений равняется произведению коэффициента самоиндукции 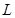 на скорость изменения тока, т. е.
на скорость изменения тока, т. е. 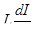 ;
;
б) разность напряжений, связанных с омическим сопротивлением, равна произведению RI (закон Ома);
в) разность напряжений на конденсаторе (по определению)
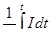 .
.
о
Таким образом, дифференциальное уравнение, описывающее явление, запишем в виде
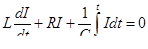
При решении этого дифференциального уравнения второго порядка для нахождения двух постоянных должны быть заданы два условия. Например, в начальный момент времени t = t 0 задаются
утопия 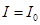 и
и 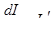 .
.
Остановимся на условиях, необходимых для решения уравнений. Если явление описывается обыкновенным дифференциальным уравнением n-го порядка, т. е. в уравнении искомая функция зависит только от одного аргумента (п — самый высокий порядок производной, входящей в уравнение, — целое число, которое может равняться единице или более), то в результате его решения должно получиться п произвольных постоянных. Для нахождения их должны быть заданы п условий. Эти условия, зависящие от характера изучаемого явления, могут быть заданы различными способами.
1. При определенном значении аргумента задается функция и ее п - 1 производные. Например, если в заданном уравнении третьего порядка искомая функция зависит от времени, то для определенного
значения времени должны быть даны функции и ее первая и вторая производные.
Такая задача называется задачей с начальными условиями, или задачей Коши.
2. При определенных значениях аргументов задаются функции и их производные. Например, если иметь дифференциальное уравнение пятого порядка, то из двух значений аргументов при одном из них даются искомая функция и ее первая и вторая производные, а при другом значении — функция и ее третья производная. Здесь в зависимости от постановки задачи возможны также различные другие варианты.
Для приведенной электрической цепи граничные условия могут быть заданы так:
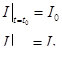
Рассмотрим механическую цепь, имеющую одну степень свободы. Напишем условие равновесия сил, действующих на пружину (рис. 26).
|
|
Рис. 26.
На пружину действуют активные силы тяжести и упругости и пассивная сила сопротивления.
Воспользовавшись принципом Д'Аламбера, условие равновесия запишем в виде
 (А)
(А)
где т — масса; h — затухание колебания; к — коэффициент жесткости; х — перемещение.
В приводимом уравнении (А) первый член по абсолютному значению представляет силу инерции, второй — силу трения, а третий — силу упругости.
Уравнение механического колебания имеет тот же вид, что и уравнение, описывающее электрическое колебание. Следовательно, в указанных уравнениях аналогичными являются параметры: х — I ,
т — L : h — R  .
.
Перейдем к безразмерным величинам следующим образом:
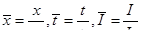
где t 0 — начальное значение аргумента; х0 и I0 — начальные значения функции. Таким образом,
 (1.93)
(1.93)
Если все члены уравнения разделить на 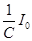 , to получим следующее уравнение с безразмерными коэффициентами:
, to получим следующее уравнение с безразмерными коэффициентами:
 (1.94)
(1.94)
|
|
Аналогично уравнение механических колебаний можно записать в безразмерном виде

Напишем начальные условия для уравнения колебаний в электрической цепи в безразмерном виде:
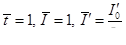
Начальные условия для уравнения механического колебание будут:
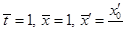
Для равенства вторых начальных условий должно быть удовлетворено следующее условие:
 (1.95)
(1.95)
Теперь, пользуясь аналогией уравнений механического и электрического колебаний, перейдем от одного уравнения к другому.
Предположим, что для механического контура т, к и h заданы. И электрическом контуре при известных 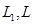 , задавшись
, задавшись 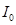 , можно найти
, можно найти 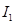 .
.
для идентичности уравнений описывающих механические и электрические колебания, необходимо
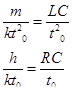 (1.96), (1.97)
(1.96), (1.97)
Тогда будут равны друг другу 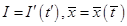 .
.
В уравнениях (1.93) и (1.94) для нахождения неизвестныхR, С, L нужно задаться одним из них. Например, задавшись значением С, можно найти R и L .
Для заданных начальных условий 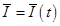 , чтобы в механической системе удовлетворить условию
, чтобы в механической системе удовлетворить условию 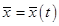 , рассмотрим выбор параметров электрического контура и начальных условий. Для этого
, рассмотрим выбор параметров электрического контура и начальных условий. Для этого 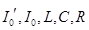 должны выбираться так, чтобы равенства (1.95) — (1.97) были удовлетворены. Например, задавшись значениями С и I'0, из этих трех уравнений можно найти I0, L и R . Выбор этих параметров зависит от места и условий опыта.
должны выбираться так, чтобы равенства (1.95) — (1.97) были удовлетворены. Например, задавшись значениями С и I'0, из этих трех уравнений можно найти I0, L и R . Выбор этих параметров зависит от места и условий опыта.
После нахождения этих параметров для установления зависимости I= I ( t ) собирается соответствующая электрическая цепь.
Гидравлическая аналогия при решении задач теплопередачи [15]
Аналитическое решение задач теплопередачи со сложными краевыми условиями и изменяющимися термическими коэффициентами (которые часто встречаются в практике) связано с большими трудностями. Применение же метода элементарных балансов связано с трудоемкими вычислительными операциями. В связи с этим созданы счетно-решающие приборы, основанные на аналогиях, облегчающих вычислительные операции. При использовании метода аналогии стремятся воспроизвести исследуемое данное явление на аналогичном явлении, которое описывается теми же математическими зависимостями, но более просто управляемом. При этом значительно облегчаются вычислительные работы.
Известны электрические модели нестационарных процессов теплопроводности (электроинтегратор Л. И. Гутенмахера); нашел применение и метод гидравлической аналогии, предложенный В. С. Лукьяновым.
Гидравлический интегратор В. С. Лукьянова основан на аналогии математических соотношений, описывающих распространение температуры в твердом теле и распределение напоров в воде, движущейся через гидравлические сопротивления при ламинарном режиме.
Основной принципиальной особенностью, определяющей устройство гидроинтегратора, является замена в гидравлическом поле равномерно распределенных параметров сосредоточенными, т. е. переход от поля к цепи с сосредоточенными параметрами. В связи с этим процесс воспроизведения непрерывного температурного поля с сосредоточенными параметрами представляет собой переход от решения дифференциальных уравнений к решению уравнения в конечных разностях.
Этот прибор состоит из основных элементов аналогии гидравлической цепи с сосредоточенными элементами сопротивлений и емкостей, а также специальных элементов, воспроизводящих выделение скрытой теплоты при изменении агрегатного состояния; устройства для задания граничных условий; приспособлений для измерения напора в узлах гидравлической цепи; устройства, обеспечивающего питание прибора водой.
Рассмотрим конкретный пример определения распределения температуры в многослойной стенке при одномерном тепловом потоке. Стенка задается размерами отдельных слоев и теплофизическими характеристиками материалов, т. е. объемными теплоемкостями ( 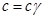 , где с — удельная теплопроводность тела;
, где с — удельная теплопроводность тела;  — объемный вес тела), и коэффициентами теплопроводности (рис. 27).
— объемный вес тела), и коэффициентами теплопроводности (рис. 27).
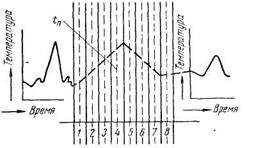
Рис. 27
Дано определенное начальное распределение температуры и произвольно выбранные воздействия температур наружных сред II тепловых потоков па поверхности стенки. Вначале составляется расчетная схема. Разбивают стенку на конечное число слоев. При этом допускается, что теплоемкость для каждого слоя сосредоточена в середине его и ограждается термическими сопротивлениями, равными половине толщины слоя.
Таким образом, расчетная схема представляет собой цепочку теплоемкостей с, разделенных между собой термическими сопротивлениями 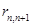 .
.
Теплоемкости крайних слоев отделены от наружной среды дополнительным термическим сопротивлением теплоотдачи с поверхности. Процесс теплообмена элементарных слоев между собой и окружающей средой определяется следующей системой уравнений:
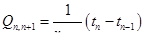 ; (1-98)
; (1-98)
 , (1-99)
, (1-99)
где  — количество тепла соответственно в слоях и,
— количество тепла соответственно в слоях и, 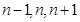 , t — температура соответствующих слоев;
, t — температура соответствующих слоев; 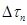 — время теплопроводности;
— время теплопроводности; 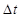 — разница температур. Гидравлическая аналогия осуществляется следующим образом. Составляется цепь из сосудов с определенными сечениями
— разница температур. Гидравлическая аналогия осуществляется следующим образом. Составляется цепь из сосудов с определенными сечениями 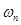 , соединенными между собой через гидравлическое сопротивление
, соединенными между собой через гидравлическое сопротивление  (рис. 28).
(рис. 28).
Число сосудов равно числу элементарных слоев. Крайние сосуды соединены с подвижными сосудами В1 и В2. Изменение уровней воды в сосудах будет определяться следующей системой уравнений:
 (1,100) (1,101)
(1,100) (1,101)
где q — расход жидкости; 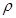 — коэффициент гидравлических сопротивлений; h — уровень жидкости в сосуде;
— коэффициент гидравлических сопротивлений; h — уровень жидкости в сосуде;  — разница уровней жидкости в сосудах.
— разница уровней жидкости в сосудах.

Рис. 28.
Расход жидкости q пропорционален разности уровней в сосудах  (аналог закона теплопроводности), а приращение содержания воды в сосуде
(аналог закона теплопроводности), а приращение содержания воды в сосуде 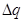 за время
за время 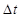 равно произведению площади сечения сосуда на приращение высоты уровня.
равно произведению площади сечения сосуда на приращение высоты уровня.
Уравнения (1.98) и (1.95) аналогичны уравнениям (1.100) и (1.101). Предположим, что цепь сосудов составлена так, что в ней величины  численно равны. Начальное распределение уровней h в соответствующем масштабе изображает начальное распределение температуры в центре элементарных слоев, а изменение уровней в подвижных сосудах происходит так же, как изменение температуры окружающих сред. Тогда уровень в сосудах будет изменяться аналогично изменению температуры в элементарных слоях. Если
численно равны. Начальное распределение уровней h в соответствующем масштабе изображает начальное распределение температуры в центре элементарных слоев, а изменение уровней в подвижных сосудах происходит так же, как изменение температуры окружающих сред. Тогда уровень в сосудах будет изменяться аналогично изменению температуры в элементарных слоях. Если 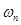 и
и 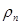 численно не равны
численно не равны 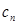 и
и 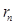 , а лишь пропорциональны им, то тепловой процесс также будет воспроизводиться на модели, по только в другом масштабе времени. Наличие такой возможности создает большие удобства, так как можно значительно ускорить воспроизведение медленных и замедлить воспроизведение быстро протекающих процессов теплообмена. В этом случае перейти от гидравлической модели к исследуемому процессу можно посредством выбора соответствующих масштабных соотношений.
, а лишь пропорциональны им, то тепловой процесс также будет воспроизводиться на модели, по только в другом масштабе времени. Наличие такой возможности создает большие удобства, так как можно значительно ускорить воспроизведение медленных и замедлить воспроизведение быстро протекающих процессов теплообмена. В этом случае перейти от гидравлической модели к исследуемому процессу можно посредством выбора соответствующих масштабных соотношений.
Если все величины, входящие в уравнения (1.98) — (1.101), выразить в безразмерных величинах, то система (1.98) и (1.99) будет подобна системе (1.100) и (1.101), так как будут равны их безразмерные множители. Отсюда получим основное выражение для масштабных соотношений.
Получаем следующие критериальные соотношения:
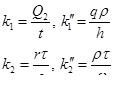
Таким образом, когда гидравлическая цепь составлена в соответствии с теплофизическими характеристиками отдельных слоев, выбирают соответствие основных величин:  и, если требуется, соответствие
и, если требуется, соответствие 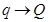 . При этом необходимым условием является равенство
. При этом необходимым условием является равенство 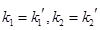 . Здесь к — безразмерные множители соответствующих физических величин; индекс
. Здесь к — безразмерные множители соответствующих физических величин; индекс  отвечает гидравлической модели, индекс
отвечает гидравлической модели, индекс 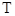 — исследуемому тепловому процессу.
— исследуемому тепловому процессу.
Пример. Допустим, что дана задача со следующими условиями. Толщина стенки 2R = 1 м, коэффициент теплопроводности бетона  = 1,667, удельная теплоемкость бетона с = 0,2, объемный вес
= 1,667, удельная теплоемкость бетона с = 0,2, объемный вес  = 200. Начальное распределение температуры задано в виде
= 200. Начальное распределение температуры задано в виде 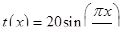 . Требуется установить распределение температур в стенке через 10 и 20 ч.
. Требуется установить распределение температур в стенке через 10 и 20 ч.

а также термическое сопротивление переходу тепла от одного слоя к другому

Для этого перейдем к составлению гидравлической модели. Ввиду симметричности температурного поля рассмотрим только половину его. Разобьем участок стенки, подлежащей исследованию (  = 0,5 м), на 10 равных по толщине слоев (n = 10). Вычислим теплоемкость одного такого слоя
= 0,5 м), на 10 равных по толщине слоев (n = 10). Вычислим теплоемкость одного такого слоя
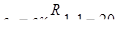
а также термическое сопротивление перехода тепла от одного слоя к другому
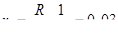
Схема разбивки поля приведена на рис. 29, схема гидравлической цепочки, тождественной по начертанию цепочке, замещающей температурное поле, на рис. 30. Крайнее сосредоточенное термическое сопротивление в два раза меньше остальных. На схеме гидравлической цепочки показаны (внизу) значения сосредоточенных сопротивлений  и гидравлических емкостей (площадей сосудов
и гидравлических емкостей (площадей сосудов  ), воспроизводящих соответствующие сосредоточенные термические величины.
), воспроизводящих соответствующие сосредоточенные термические величины.
Для масштабных соотношений принимаем следующее соответствие 20 см напора  20° С; 0,3 мин/см2 гидравлического сопротивления
20° С; 0,3 мин/см2 гидравлического сопротивления  0,03 ч°С/ ккал термического сопротивления слоя; 2 см2 площади сосуда
0,03 ч°С/ ккал термического сопротивления слоя; 2 см2 площади сосуда  20 ккал/°С теплоемкости слоя.
20 ккал/°С теплоемкости слоя.
|
|
Рис. 29. Рис. 30.
|
|
Вычислим масштаб времени 
Так как требуется установить распределение температур в стенке через 10 и 20 ч от начала теплового процесса, то первая остановка прибора должна
|
|
быть через 10 ч, а вторая через 20 ч от начала теплового процесса. Следовательно, первая остановка прибора должна быть через 10 мин, а вторая — через 20 мин после пуска. Для задания на приборе начального состояния вычисляем значения функции 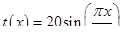
в точках х = 0,025; 0,075; 0,125; 0,475 м (рис. 31). Полученные величины будут заданы как
рис. 31
начальные напоры в сосудах гидравлической модели. Граничное условие на поверхности стенки t = 0° С будет воспроизведено на приборе подключением с левой стороны цепочки сосуда с постоянным уровнем воды в нем, соответствующем 0° С.
На правом крае цепочку следует отключить в соответствии с условием симметрии  (т. е. поток тепла во время теплового процесса равен нулю).
(т. е. поток тепла во время теплового процесса равен нулю).
На рис. 31 приведена кривая начального распределения температур и кривые, рассчитанные на приборе распределений температур через 10, 20 и 40 ч от начала процесса. Следует отметить, что отклонения нигде не превосходят 1,5 мм, т. е. 0,15° С.
На гидроинтеграторе можно решать одно-, двух- и трехмерные задачи.
Для решения одномерных задач соединяют сосуды в цепочки. При решении двухмерных задач требуется соединить цепочки из сосудов между собой посредством сопротивления в соответствии с принятой разбивкой исследуемого температурного поля на блоки. возможно также и решение трехмерных задач, но так как при этом такое число сосудов равно 100, то схема разбивки поля на отдельное блоки должна быть заранее продумана.
В приведенных выше примерах аналогии для ясности были рассмотрены простые явления. Однако этот метод применим и для исследования отдельных сложных явлений, встречающихся в различных областях техники.
Аналогия между механическими и электрическими системами
| N | механика | схема | Электрический аналог | схема | ||
| 1 | Упругое тело | P = kтрSv = RMv | 
| Двухполюсник с активным сопротивлением | U=I*R | 
|
| 2 | Вязкое тело |
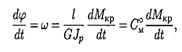
| 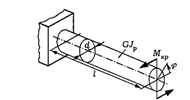
| Двухполюсник с емкостью | 
| 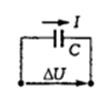
|
| 3 |
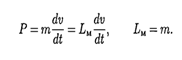

| 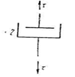
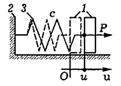
| Двухполюсник с индуктивностью | 
| 
|
Дата: 2019-05-28, просмотров: 337.