Пусть вязко – пластичная жидкость с плотностью 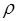 , вязкостью η и динамическим напряжением сдвига τ0 движется со скоростью
, вязкостью η и динамическим напряжением сдвига τ0 движется со скоростью  в трубопроводе с внутренним диаметром d, длиной l,произвольно расположен-ном пространстве, если в сечениях 1 и 2 давления равны соответственно Р1 и Р2
в трубопроводе с внутренним диаметром d, длиной l,произвольно расположен-ном пространстве, если в сечениях 1 и 2 давления равны соответственно Р1 и Р2
(рисунок 1.1). Сечения 1 и 2 могут представлять собой соответственно начало и конец трубопровода или любого произвольно выделенного участка.
Пространственное положение трубопровода может быть задано некоторым безразмерным параметром , например зенитным и азимутальным
углами для любой глубины. Параметр может оставаться неизменным
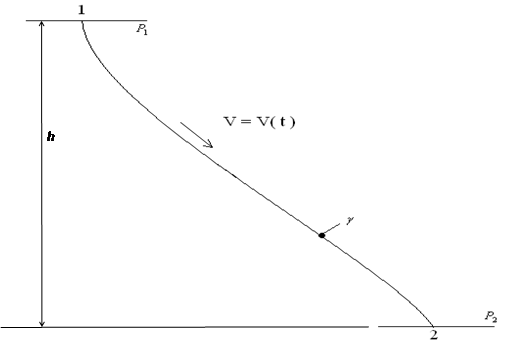 |
Рисунок 1.1 - Трубопровод с произвольным расположением в пространстве
по длине трубопровода либо изменяться по любой пространственной кривой.
Введение в рассмотрение (помимо зенитного) и азимутального угла может быть вызвано необходимостью учета Кориолисова ускорения в движущейся жидкости.
Запишем для рассматриваемого процесса следующее функциональное уравнение:
F ' (d, l, γ, t, ρ, η, τ0, V, P1, P2,) = 0. (1.38)
В этом уравнении штрих при символе функциональной зависимости означает то, что вид ее, возможно, еще не окончательный, и ее предстоит уточнить. Это обычно бывает связано, с одной стороны, со стремлением сократить число параметров, а с другой – с тем, что не все параметры сразу же удается выбрать удачно ввиду малоизученности или сложности рассматриваемого процесса.
Уточнение может быть произведено постановкой предварительных, так называемых отсеивающих, экспериментов, но чаще – путем тщательного анализа сути и содержания принятых в рассмотрение параметров. В последнем случае обычно пользуются так называемым методом последовательного развертывания и детализации параметров. Этот метод заключается в том, что некоторые сложные параметры, зависящие, в свою очередь, от других параметров (если таковые имеются), записываются в виде функций других, более простых параметров и вводятся в исходное уравнение (1.38). После этого исходное уравнение обычно становится переопределенным в том смысле, что некоторые параметры встречаются более одного раза. Далее повторяющиеся параметры исключаются, так что каждый параметр учитывается лишь один раз.
Необходимость в детализации параметров обычно бывает связана с тем, что составляющие сложного параметра различным образом влияют на исследуемый процесс, или же тогда, когда вновь вводимые параметры бывают в каких – то отношениях удобнее первоначально принятых, например, при измерениях или расчетах.
Покажем это на рассматриваемом примере.
Для задач из области гидравлики сокращение числа параметров обычно достигается заменой давлений P1 и Р2 их разностью, т.е. перепадом давления ΔP = P1 – P2. Однако это возможно не всегда. Замена давлений 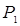 и
и 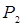 на их разность означает исключение из рассмотрения давления
на их разность означает исключение из рассмотрения давления 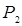 и, стало быть, уменьшение давления в гидравлической системе на эту величину. Это допустимо лишь в том случае, если нас интересует только гидродинамика процесса между сечениями 1 и 2, а величина абсолютного давления никакой роли не играет. Между тем она может интересовать нас, например, с точки зрения прочности трубопровода. Но если же по условию задачи это возможно, то дальнейшее сокращение числа параметров может быть достигнуто заменой перепада давления на градиент давления
и, стало быть, уменьшение давления в гидравлической системе на эту величину. Это допустимо лишь в том случае, если нас интересует только гидродинамика процесса между сечениями 1 и 2, а величина абсолютного давления никакой роли не играет. Между тем она может интересовать нас, например, с точки зрения прочности трубопровода. Но если же по условию задачи это возможно, то дальнейшее сокращение числа параметров может быть достигнуто заменой перепада давления на градиент давления 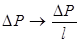 . При этом число параметров, как нетрудно заметить, сокращается сразу на две единицы.
. При этом число параметров, как нетрудно заметить, сокращается сразу на две единицы.
В общем случае давление в начале трубопровода, т.е. суммарное давление, можно записать так:
 , (1.39)
, (1.39)
где 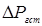 – гидростатическое давление, определяемое разностью геометрических высот расположения сечений 2 и 1;
– гидростатическое давление, определяемое разностью геометрических высот расположения сечений 2 и 1;
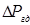 – потери давления на участке трубопровода между сечениями 1 и 2.
– потери давления на участке трубопровода между сечениями 1 и 2.
Представим (1.39) в виде
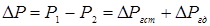
и поделим обе части этого уравнения на l . Тогда получим
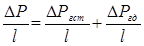 , (1.40)
, (1.40)
где члены правой части (1.40) суть градиенты соответствующих давлений.
Заметим, что в гидравлике 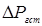 принято относить не к длине трубопровода, а к разности геометрических высот расположения его концевых участков, что называется гидравлическим уклоном.
принято относить не к длине трубопровода, а к разности геометрических высот расположения его концевых участков, что называется гидравлическим уклоном.
Так как разность геометрических высот сечений 2 и 1 в рассматриваемой задаче равна ( 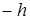 ) (сечение 2 расположено ниже сечения 1), то
) (сечение 2 расположено ниже сечения 1), то
 , и
, и
(1.40) принимает вид
 , (1.41)
, (1.41)
где 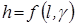 ; (1.42)
; (1.42)
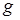 – гравитационная постоянная.
– гравитационная постоянная.
Сопоставляя полученные выражения (1.41) и (1.42) с исходным уравнением (1.38), а также с учетом того, что параметры 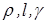 в (1.38) уже присутствуют, приходим к выводу, что 3 параметра
в (1.38) уже присутствуют, приходим к выводу, что 3 параметра  ,
, 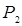 и
и  в (1.38) можно заменить на 2 параметра:
в (1.38) можно заменить на 2 параметра: 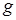 и
и 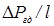 в окончательном уравнении, если абсолютное давление интереса не представляет. В противном случае
в окончательном уравнении, если абсолютное давление интереса не представляет. В противном случае 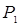 необходимо оставить.
необходимо оставить.
Здесь могут быть следующие две ситуации:
1) сечение 2 является концевым, и жидкость свободно вытекает в атмосферу. Тогда
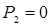 и
и 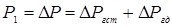 . (1.43)
. (1.43)
Наибольшее давление в системе  здесь обусловлено только разностью высот расположения сечений 2 и 1 и потерями давления на участке трубопровода между ними;
здесь обусловлено только разностью высот расположения сечений 2 и 1 и потерями давления на участке трубопровода между ними;
2) сечение 2 не является концевым, и давление в нем не равно нулю, т.е. 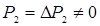 , причем
, причем 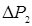 может представлять собой как сумму распределенных по длине потерь давления на участке любой протяженности за сечением 2, так и сосредоточенный перепад давления сразу же за сечением 2, или же то и другое одновременно.
может представлять собой как сумму распределенных по длине потерь давления на участке любой протяженности за сечением 2, так и сосредоточенный перепад давления сразу же за сечением 2, или же то и другое одновременно.
Пусть абсолютное значение давления Р1 представляет для нас интерес, что соответствует более общему случаю. Тогда функциональное уравнение окончательно запишется в виде
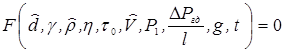 . (1.44)
. (1.44)
Размерности параметров следующие:
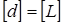 ;
; 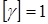 ;
;  ;
; 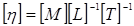 ;
; 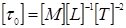 ;
;
 ;
; 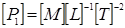 ;
;  ; [g] = [L] [T]-2; [t] = [T];
; [g] = [L] [T]-2; [t] = [T];
В (1.44) 10 параметров связаны одним уравнением связи и должны дать 7 критериев подобия, форма записи которых будет зависеть от выбора основных единиц. Теоретически число таких возможностей равно числу сочетаний из 7 элементов по 3, т.е.  . Но в действительности их будет меньше, ибо легко заметить, что некоторые тройки параметров взаимозависимы, например d , t , g; d , g , V и др. Поэтому N < 35. Из них один безразмерный параметр γ при любом выборе основных единиц сразу же дает критерий подобия.
. Но в действительности их будет меньше, ибо легко заметить, что некоторые тройки параметров взаимозависимы, например d , t , g; d , g , V и др. Поэтому N < 35. Из них один безразмерный параметр γ при любом выборе основных единиц сразу же дает критерий подобия.
Выберем в качестве основных единиц d , ρ, V (в (1.44) они выделены дугообразной черточкой наверху) и запишем функциональное уравнение в критериальной форме:
 , (1.45)
, (1.45)
где индексы при Р и 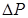 в целях простоты опущены.
в целях простоты опущены.
Обозначим:
 ;
; 
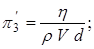
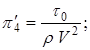
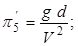
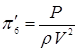 ;
; 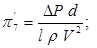
Здесь и далее критерии подобия снабжены штрихами в связи с тем, что такая форма записи, возможно, не окончательная, и они нуждаются в другой, более привычной форме записи.
Если в качестве основных единиц взять тройку параметров d , V , η, то получим
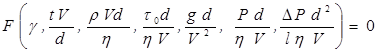 . (1.46)
. (1.46)
Здесь 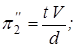


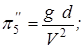
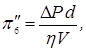
 .
.
Дата: 2019-05-28, просмотров: 340.