составленных из масштабов подобия, и их решение

Запишем полученные критерии подобия (для простоты - без критерия ):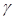

; ; ; ; .

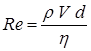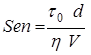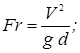
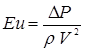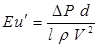Величины, относящиеся к натуре и модели, снабдим индексами н  и м. Тогда

;

;

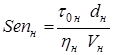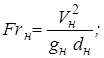
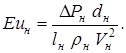
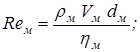
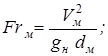
Составим отношения критериев подобия модели и натуры. Например, для критерия Рейнольдса получим

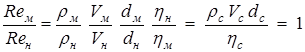,                                                    (1.48)

где отношения одноименных параметров обозначены теми же буквами с индексом с. Комплексный параметр , составленный из масштабов подобия, представляет собой индикатор подобия. Он имеет следующее определение:

Комплексы и симплексы, составленные из масштабов подобия и совпадающие по форме алгебраической записи с критериями подобия, называются индикаторами подобия.

Индикаторы подобия для остальных критериев подобия будут следующие:

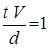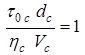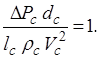; ; ;                          (1.49)

От индикаторов подобия легко перейти к системе уравнений, составленных из масштабов подобия:

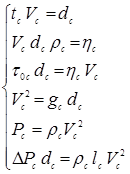                                                                                        (1.50)

Пусть выбран масштаб подобия, например, d_c = λ . Тогда

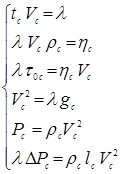                                                                                        (1.51)

Из последнего уравнения системы следует, что при наличии геометричес-кого подобия линейные (диаметральные и осевые) размеры моделируются в одном и том же масштабе. Поэтому l_c = d_c = 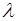, и пятое уравнение в (1.51) переходит в следующее: .

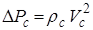Из четвертого уравнения системы имеем

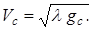                                                                                              (1.52)

Подставив его в первое уравнение, получим масштаб времени

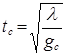
Подставив (1.52) во второе уравнение, будем иметь

.                                                                                           (1.53)

Из третьего уравнения с учетом (1.52) получим

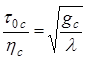.                                                                                           (1.54)

И, наконец, из (1.53) и (1.54) получаем

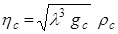и                                                                                    (1.55)

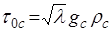.                                                                                         (1.56)

Таким образом, масштабы по структурной вязкости и пластической прочности структуры вязко - пластичной жидкости сложным образом зависят от принятого масштаба геометрического подобия и гравитационной постоянной.

При изменении плотности жидкости, как отмечалось выше, изменяется и ее вязкость, изменяется также и динамическое напряжение сдвига, и совсем непросто приготовить модельную жидкость. Поэтому желательно было бы иметь дело с одной и той же жидкостью, при которой . Но тогда из (1.55) получим , а из (1.56) 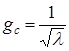, т.е. придем к явному противоречию. Более того, в земных условиях применительно к данной задаче невозможно выбрать масштаб g _с, отличный от единицы. Поэтому эта задача будет иметь единственное решение: 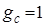, при этом  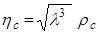и 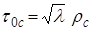, что может быть достигнуто лишь путем тщательного подбора соотношения   и   при данной плотности жидкости 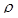, на которую никаких ограничений не накладывается.

В зависимости от плотности жидкости давление и перепад давления будут моделироваться в одном и том же масштабе 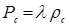 и . Отсюда хорошо видно, что обеспечение подобия характеристик жидкостей вообще и вязко – пластичных жидкостей в особенности встречает серьезные

трудности. Аналогичные трудности возникают при решении многих других

задач механики и в других областях знаний.