Критерии подобия в этом случае можно получить на основе анализа размерностей.
Измерить какую-либо величину - значит сравнить её с другой величиной той же природы, значение которой известно и принято за эталон.
Единицы измерения различных физических величин, объединенные на основе непротиворечивости друг другу, образуют систему единиц измерения.
В настоящее время применяется Международная система единиц измерения СИ (System International), принятая в начале 70-х годов прошлого столетия.
В системе СИ выбраны следующие, независимые друг от друга величины измерения: массы – кг (килограмм); длины – м (метр), времени – с (секунда); температуры – K (градусы Кельвина); силы тока – А (ампер); количества вещества – n (моль) и силы света – Y (свеча, или кандела); Они называются первичными единицами измерения. Через них выражаются все остальные единицы измерения, которые называются вторичными, или производными.
Для решения задач в области механики достаточно иметь три первичные единицы измерений: мер длины, массы и времени. В качестве эталона длины до недавнего времени служил платиновый метр, хранившийся в Парижской палате мер и весов. Эталоном массы является платиновая гиря в один килограмм, хранящийся там же. За эталон времени считали 1/86400 часть земных суток. После принятия системы СИ прототипы некоторых эталонов мер были уточнены: в настоящее время метр есть длина пути, проходимого светом в вакууме за интервал времени, равный 1/299 792 458 с;
секунда равна 9192631770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия – 133;
ампер равен силе неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводам бесконечной длины и ничтожно малой площади поперечного сечения, расположенным в вакууме на расстоянии 1м один от другого, вызвал бы на каждом участке проводника длиной в 1м силу взаимодействия, равную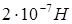 
(Ньютон);
градус Кельвина равен 1/273,16 части термодинамической температуры тройной точки воды;
моль равен количеству вещества системы, содержащей столько же
структурных элементов, сколько содержится атомов в углероде -12 массой 0,012 кг;
кандела равна силе света в заданном направлении источника, испускающего монохроматическое излучение частотой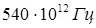 
(герц), сила излучения которого в этом направлении составляет 1/683 Вт/ср (ватт на стерадиан).
Кроме приведенных величин допускаются к использованию кратные и дольные единицы измерения, а также большое множество внесистемных единиц, нашедших широкое применение в различных отраслях народного хозяйства. Следует, однако, иметь в виду, что при выполнении вычислений в расчетных формулах рекомендуется использовать производные величины с размерностями, выраженными через первичные величины, что исключает вероятность ошибок, связанных с применением кратных или дольных единиц измерения.
Формула, указывающая зависимость единицы измерения производной величины от основных единиц измерения, называется размерностью этой величины. Например, определительным уравнением для скорости является уравнение V = dl / dt .
Принято использовать следующие символы для выражения размерностей
величин: М – масса, L – длина, Т – время, θ – градусы температуры, I – сила тока, n – количество вещества Y – сила света.
Аналогичные символы используются также для выражения производных величин. Например: F – сила, А – работа, N – мощность и т.д. Системой СИ они не регламентируются.
Символы обычно помещаются в квадратные скобки. Например, для скорости это будет выглядеть так: [V] = [L] [T]-1.
Поскольку определительное уравнение для силы согласно второму закону Ньютона есть F = m a, то [F] = [M] [L] [T]-2.
Для работы A = F S; S – длина пути, [A] = [M] [L]2 [T]-2 .
Необходимо иметь в виду, что размерность любой физической величины представляет собой произведение возведенных в какие – либо степени размерностей первичных величин.
Хотя число первичных величин в общем случае равно семи, обычно не все они одновременно используются при решении конкретных задач, причем тип используемых величин зависит от области знаний или техники, к которой относится данная задача. Так, для механической системы достаточно трех первичных величин: длины, массы, времени. Поэтому размерность любой физической величины Q в механической системе может быть выражена через размерности этих трех первичных величин следующим образом:
[Q] = [M]α [L]β [T]γ,
где пока неизвестные показатели степени α, β, γ подлежат определению.
Интересен вопрос: можно ли вместо первичных величин выбрать какие – либо иные (производные, т.е. непервичные) величины u1, u2, u3.? Если да, то когда это возможно? Такой вопрос возникает в связи с тем, что процедура получения критериев подобия заключается в освобождении от размерностей входящих в функциональное уравнение параметров путем использования размерных величин. Ясно, что если в функциональном уравнении имеются параметры, размерности которых совпадают с размерностями первичных величин, то получение критериев подобия с их использованием не составит труда. Однако такая ситуация наблюдается редко. Гораздо чаще встречаются ситуации, когда число параметров в функциональном уравнении с простейшими размерностями менее трех. Тогда– то и возникает необходимость выбора производных величин, по крайней мере, одного или двух вместо первичных.
Для ответа на этот вопрос выразим эти новые величины через старые: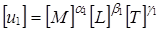 
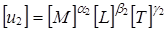(1.11)
Прологарифмировав (1.11), будем иметь:
lg [u1] = α1∙lg [M] + β1∙lg [L] + γ1∙lg [T]
lg [u2] = α2∙lg [M] + β2∙lg [L] + γ2∙ lg [T] (1.12)
lg [u3] = α3∙lg [M] + β3∙lg [L] + γ3∙lg [T],
т.е. получим систему уравнений, из которой можно найти коэффициенты при условии, что определитель, составленный из них, отличен от нуля, причем это решение будет единственное.
Составим определитель
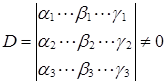(1.13)
Условие (1.13) означает также независимость величин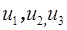 
. Тогда приходим к следующему заключению. Для получения критериев подобия вместо первичных величин можно выбрать любые три величины при условии:
1) размерности величин u1, u2, u3 являются независимыми функциями первичных размерностей [M], [L] и [T], т.е.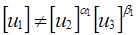 
; 
; 
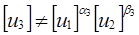при любых 
и 
;
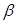2) возможно однозначное обратное преобразование, т.е.[M], [L] и [T] можно единственным образом выразить через [u1], [u2] и [u3].
Например, если взять величины L, T и F, то
[L] = [M]0 [L]1 [T]0; [T]= [M]0 [L]0 [T]1; [F] = [M]1 [L]1 [T]-2.
Тогда определитель равен
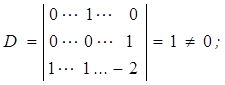
3) эти три величины должны дать в совокупности размерности всех трех первичных величин.
Выбранные таким образом три параметра называются основными параметрами.
Совершенно ясно, что эти фундаментальные положения будут справедливы для любого числа первичных величин.
Проверить самостоятельно: можно ли в качестве основных выбрать параметры: 1) F, ρ, t; 2) F, V, N,
где F – сила; ρ – плотность; t – время; V – скорость; N - мощность.
Размерности некоторых производных величин будут следующие:
1) Площадь S = l2 = > [L]2.
2) Объем Q = l3 => [L]3.
3) Момент силы M = F ∙ l => [M]∙ [L]2 ∙[T]-2.
4) Момент инерции I = m ∙ l2 => [M]∙[L]2.
5) Мощность N = A / t => [M]∙[L]2∙[T]-3.
6) Давление P = F / S =>[M]∙[L]-1[T]-2.
7) Плотность ρ = m / V => [M]∙[L]-3 .
8) Динамическая вязкость 
9) Кинематическая вязкость 
.
1.7 Вторая теорема подобия (π – теорема)
Вторая теорема основана на результатах исследований Букингема, Федермана и Афанасьевой – Эренфест. Возможность представления интеграла как функции от критериев подобия, найденных из дифференциального уравнения, была строго доказана для частного случая Букингемом, а в более общем виде как математическая теорема – Федерманом. Возможность получения критериев подобия при отсутствии дифференциального уравнения процесса на основе анализа размерностей физических величин, участвующих в этом процессе, была строго доказана в виде теоремы Афанасьевой – Эренфест.
Эта теорема является настолько важной, что ей дали специальное название π – теорема. Она позволяет получить критерии подобия и в тех случаях, когда уравнение процесса можно представить лишь виде
функциональной зависимости между параметрами системы и процесса:
y = f (x1, x2,…,xj ,…, xn -1),или
F (y, xl, x2,....,xj,....,xn - l) = 0, (1.14)
где f и F означают лишь символы зависимости.
π – теорема имеет несколько формулировок, одна из которых (основная) следующая. Всякое полное уравнение физического процесса, записанное в определенной системе единиц, может быть представлено в виде функциональной зависимости между критериями подобия, полученными из участвующих в процессе параметров.
Покажем применение 
– теоремы на известном примере с колебаниями груза массой m на пружине с жёсткостью С в вязкой среде, сила сопротивления которой пропорциональна скорости V, т.е.
F с= – k V;
на груз действует возмущающая сила F. Отклонение груза от состояния равновесия обозначим через х.
Запишем для него следующую функциональную зависимость:
x = f (m, С, t, F0, ω, k), или
F (m, С, x, t, F0, ω, k) = 0. (1.15)
Число критериев подобия всегда равно разности между числом участвующих в процессе параметров n и основных параметров r. Поскольку данная задача - из области механики, то r = 3, и эти n (семь) величин должны дать n – r (7 – 3 = 4) критерия подобия.
1.7.1. Способы получения критериев подобия на основе π – теоремы
Классический способ
Обозначая критерии подобия через π, можем записать
π = [m]z1∙ [С]z2 ∙[x]z3 [t]z4∙ [F0]z5∙ [ω]z6∙ [k]z7. (1.16)
Показатели степеней zl, z2,..., z7 должны быть определены так, чтобы размерность π была равна нулю (π в нулевой степени равно единице).
Далее вместо m, С,..., k подставляются их размерности через первичные единицы измерений:
[Pi]=[L]αi [M]βi [T]γi, (1.17)
где Pi – любой из 7 параметров.
Подставляя (1.17) в (1.16), получаем
π =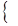 
[L]α1 [M]β1 [T]γ1 
z1∙ 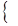[L]α2 [M]β2[T]γ2 z2 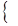[L]α7 [M]β7 [T]γ7 z7. (1.18)
Значения показателей степени z1, z2,...,z7 определяются из решения следующей системы:
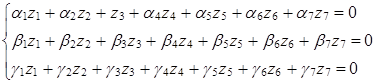(1.19)
Система (1.19 )имеет n -– r (7 – 3 = 4) независимых решения. Каждое решение должно дать один критерий подобия. Следовательно, необходимо
Таблица 1.1- Размерности физических величин
| Параметр | Показатель степени | ||
| [L] | [M] | [T] | |
| m | α1= 0 | β1 = 1 | γ1 = 0 |
| С | α2 = 0 | β2 = 1 | γ2 = – 2 |
| x | α3 = 1 | β3 = 0 | γ3 = 0 |
| t | a4 = 0 | β4 = 0 | γ4 = 1 |
| F 0 | а5 = 1 | β5 = 1 | γ5 = – 2 |
| ω | a6 = 0 | β6 = 0 | γ6 = – 1 |
| k | а7 = 0 | β7 = 1 | γ7 = – 1 |
решить систему уравнений (1.19).
Степени размерности параметров представлены выше в виде таблицы 1.1.
Тогда система (1.19) упростится и примет вид
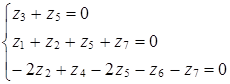(1.20)
Система (1.20) имеет 4 линейно независимых решения. При этом четыре величины zi могут принять произвольные значения, остальные три определяются из уравнений системы.
Произвол в выборе некоторых чисел zi не имеет никакого значения. Важно лишь одно – чтобы π стало безразмерной величиной. Поэтому для них выбирают наиболее простые значения, но так, чтобы уравнения системы не противоречили друг другу. Например, нельзя дать произвольное значение для z1, z2, z3 и z7 т.к. в этом случае первое и второе уравнения будут противоречить друг другу.
1 Принимаем z1 = l, z2 = z6 = z7 = 0. Тогда: z3 + z5 = 0; l + z5 = 0;
z4 - 2 z5 = 0. Отсюда получаем: z5 = - l, z3 = l, z4 = -2.
Итак, первое решение: z1 = l, z2 = 0, z3 = l, z4 = -2, z5 = -l, z6 = 0, z7 = 0.
2 Пусть z1 = 0, z2 = 1, z6 = z7 = 0.
Тогда получаем z3 + z5 =0, 1 + z5 = 0, 2 + z4 - 2z5= 0.
Отсюда получаем z5 = - l, z3 = l, z4 = 0, z6 = z7 = 0.
Поэтому второе решение будет: z1 = 0, z2 = l, z3 = l, z4 = 0, z5 = -l, z6 = 0, z7 = 0.
3 Принимаем z1 = z2 = 0, z6 = 1, z7 = 0.
Тогда z3 + z5 = 0, z5 = 0, z4 - 2z5 – l = 0.
Отсюда z5 = 0, z3 = 0, z4 = l.
Следовательно, третье решение: z1= 0, z2 = 0, z3 = 0, z4 = 1, z5 = 0, z6 = l, z7 = 0.
4 z1 = z2 = z6 = 0, z7 = l.
Тогда z3 + z5 = 0, z5 + l = 0, z4 - 2z5 - l= 0.
Отсюда z5 = - l, z3 = l, z4 = - 1.
Таким образом, получены все четыре решения, которым соответствуют четыре критерия подобия.
Из первого решения получаем критерий
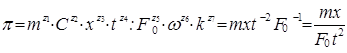. (1.21)
Из второго решения:
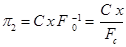. (1.22)
Из третьего решения:
. (1.23)
Из четвертого решения:
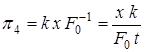. (1.24)
Дата: 2019-05-28, просмотров: 322.
