Получить критерии подобия на основе π – теоремы упрощенным способом для колебания груза с массой m на пружине с жесткостью С в вязкой среде, сила сопротивления которой пропорциональна скорости V, если на груз действует возмущающая сила F0 s in ω t; t- время.
Пусть отклонение груза от состояния равновесия равно х.
Запишем функциональную зависимость:
F (m , x , t ,С ,ω , k , F 0 ) = 0. (1.30)
Имеющиеся 7 величин должны дать 7 – 3 = 4 критерия подобия.
Выбираем основные единицы. Максимально возможное число троек (вариантов) равно: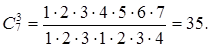 
Ясно, что перебрать все эти варианты можно, но довольно громоздко. Памятуя, что выбор основных единиц – вопрос не принципиального характера, а диктуется в большей мере лишь соображением удобства, рассмотрим лишь некоторые из вариантов, придерживаясь в то же время сформулированных выше правил.
1 Вариант. Вначале в качестве основных примем параметры m, x и t, т.е.параметры с самыми простыми размерностями, соответственно [М], [L] и [Т], символически совпадающими с первичными единицами измерения.
Ясно, что эти параметры взаимно независимы.
Размерности остальных величин следующие:
[С]=[М][Т]-2 ; ω=[Т]-1; [k]= [М][Т]-1 ; [F 0]=[M][L][T]-2.
Приводим все оставшиеся четыре параметра к безразмерному виду.
Для этого первый из них записываем в числитель, указывая, справа от него
его размерность: С => [М] [Т]-2.
Совершенно очевидно: чтобы привести к безразмерному виду, в знаменателе дроби нужно вначале записать параметр - основную единицу m в первой степени, а параметр t - в степени 2. В результате получим первый критерий подобия в виде
(1.31)
Аналогично приводим остальные параметры к безразмерному виду, что легко проследить по записи:
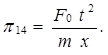(1.32)
В полученных критериях первый индекс означает номер варианта.
Сравнивая их с ранее полученными по классическому методу критериями, легко установить, что:
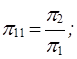
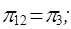
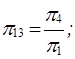
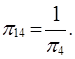
Отсюда видим, что критерии подобия по этому способу получаются весьма быстро.
2 Вариант. Примем теперь в качестве основных единиц параметры х, k и F0, т.е. параметры не с самыми простыми размерностями, что противоречит правилу 2. Ясно, что этот вариант мы рассматриваем лишь с целью показать, какие трудности могут возникать, если не придерживаться правил.
Проверяем независимость выбранных основных единиц. Так как
,
то они независимы.
Остальные четыре параметра следующие: m, t, с и 
.
Записав в числитель дроби m и справа - его размерность [М], видим, что от этой размерности можно избавиться, записав в знаменатель дроби и k, и F0. Причем часто бывает затруднительно усмотреть, что быстрее ведет к цели, а что нет или ведет ли оно к цели вообще. Пусть это будет F0. Тогда получим
.
Теперь видно, что возникла трудность с освобождением от размерности [Т]. Если теперь записать в знаменатель параметр k в степени – 2, то получим
Только теперь стало ясно, что этот путь не ведет к цели. Поэтому
приходится все начать сначала. Если в знаменатель записать k, то 
.
Для того, чтобы освободиться от Т, необходимо теперь в знаменатель записать F0 в степени минус 1/2 , т.е.
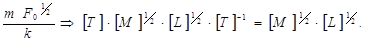
Теперь задача усложняется тем, что надо освободиться от размерности [М] и [L], причем в степени ½. Если теперь записать в знаменатель дроби k 1/2, то от [М] освободимся, но опять появится [Т ] в степени 1/2.
В то же время решение есть. Необходимо записать так:
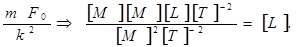
Далее, чтобы освободиться от [L], нужно в знаменатель записать х.
Тогда получаем
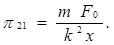(1.33)
Отметим, что это не всегда бывает очевидно.
Аналогично можно получить и остальные критерии подобия. Опуская промежуточные рассуждения и выкладки, запишем их в окончательном виде:
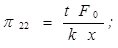
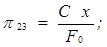
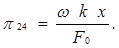(1.34)
Сопоставляя эти критерии с критериями, полученными по варианту 1, устанавливаем, что
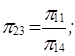
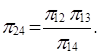
В заключение отметим, что если выбранные в качестве основных единиц параметры независимы, то критерии подобия можно получить всегда. Дело лишь в том, что их получение значительно более трудоемко.
Рассмотрим ряд задач из области гидродинамики.
Вначале рассмотрим самую простую задачу.
Пусть жидкость с плотностью ρ, вязкостью η движется равномерно со средней по сечению трубы скоростью V в горизонтально расположенной трубе с внутренним диаметром d .
Имеем
V = f ( d, ρ, η), или F ( d, ρ, η, V ) = 0. (1.35)
Их размерности следующие:
; 
, 
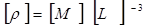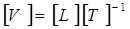и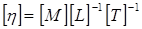 
, т.е. наиболее простую размерность имеет параметр d; размерности, включающие размерности двух первичных единиц измерения, параметры - 
и V, а наиболее сложную размерность в виде комбинации размерностей всех трех первичных единиц имеет единственный оставшийся параметр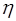 
.
В соответствии с оговоренными выше правилами выбираем в качестве основных единиц параметры d, ρ и V и приводим (1.35) к критериальному виду. Записываем в числитель дроби параметр 
, указывая справа его размерность, а в знаменатель основные параметры подставляем в следующей последовательности: вначале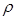 
в степени плюс единица, что позволяет освободиться от размерности 
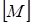, затем V в плюс первой степени, освобождаемся от размерности 
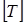и понижаем степень 
. Далее, подставляя d в плюс первой степени, освобождаемся окончательно от всех размерностей. В результате получаем критерий подобия в форме
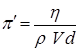. (1.36)
Это обратная величина критерия Рейнольдса, широко применяемого при решении задач гидродинамики. Поэтому приводим (1.36) к привычной форме
записи
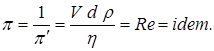(1.37)
Преимущества критериального представления процесса трудно переоценить. Первое очевидное преимущество заключается в сокращении числа параметров. Так, в только что рассмотренном примере вместо четырех параметров с различными размерностями вводится в рассмотрение лишь один комплексный параметр – критерий подобия.
Второе преимущество заключается в том, что при проведении экспериментов легко добиться гидродинамического подобия процессов, изменяя лишь один параметр, например V, тогда как изменение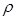 
или η связано с выбором другой жидкости, трудностями обеспечения подобия по ним , a изменение d означает выбор других труб.
Теперь рассмотрим более общий случай.
Дата: 2019-05-28, просмотров: 203.
