Критерии подобия можно получить и другим, несколько видоизмененным способом. Выбрав какие-либо 3 параметра по числу основных единиц измерения – метр, килограмм, секунда, – для которых определитель не равен нулю, можно прийти к безразмерным соотношениям.

Выберем в качестве основных единиц, например, параметры m , ω , F₀. Проверим их независимость. Их размерности следующие:

[m] = [M]¹ [L]⁰ [T]⁰, [ω] = [M]⁰ [L]⁰ [T]^-1, [F₀] = [M] [L] [T]^-2.

=

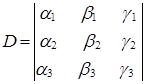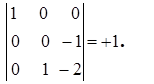
Запишем уравнение (1.16) в следующей форме:

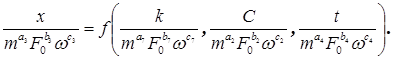                        (1.25)

В этом уравнении индексы при показателях степени соответствуют порядковому номеру параметров в уравнении (1.16).

Значения показателей степеней при a, b и с  определяют из условия, что входящие в (1.25) комплексы – безразмерные величины.

1)

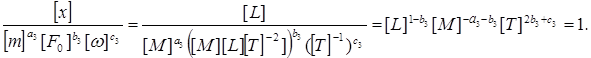
Отсюда получаем 1 - b₃ = 0; b₃=1; -a₃ - b₃=0; a₃ = -1; 2b₃ + c₃=0; c₃ = -2.

Поэтому

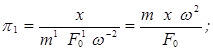                                                               (1.26)

2)

Имеем

b ₇ = 0; 1- a₇ - b₇ = 0; - 1 + 2 b₇ + с₇ = 0;

Отсюда получаем: a₇ = -1; c₇ = 1.

Следовательно

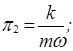                                                                                              (1.27)

3)

Имеем   b₂  = 0; 1 - a₂ - b₂ = 0; -2 + 2b₂ + c₂ = 0;

В результате получаем a₂ = 1; c₂ = 2.

Поэтому

                                                                                           (1.28)

4)  

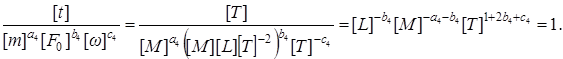
Имеем -b₄ = 0; - a₄ - b₄ = 0; 1 + 2b₄ + c₄ = 0;

Отсюда b₄ = 0; a₄= 0; c₄ = -1;

Следовательно,

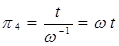.                                                                                  (1.29)

Ранее было получено

.

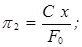
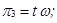
Здесь получено

      .

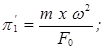
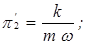
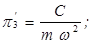
Нетрудно увидеть, что

; π ₄ ^’ = π ₃ ; .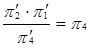

Поскольку любая комбинация критериев представляет также критерий подобия, то результат, конечно же, получился тот же, только изменилась форма их записи.

Упрощенный способ

Рассмотренные выше способы получения критериев подобия являются строгими, хотя и несложными, но довольно громоздкими, требующими времени.

Критерии подобия можно получать и более простыми способами, не требующими составления уравнений и их решения. Вся эта процедура как бы проделывается в уме, и критерии получаются сразу же.

Последовательность работ при этом следующая:

1) составляется функциональная зависимость между параметрами;

2) выбираются параметры в качестве основных. Их число должно быть равно числу первичных единиц измерения. В механике их три. Поэтому при решении задач из области механики параметры, выбранные в качестве основных, должны в совокупности дать меры массы, длины и времени;

3) указываются размерности выбранных параметров, проверяется их независимость;

4) указываются размерности всех оставшихся параметров;

5) в числитель дроби последовательно выписывается каждый из n - r оставшихся параметров, а в знаменатель - выбранные в качестве основных в соответствующих степенях так, чтобы полностью освободиться от размерности этой дроби. При выполнении этих работ следует придерживаться определенных правил. Они следующие.

1 При составлении функционального уравнения следует учитывать по возможности все параметры, которые, по мнению исследователя, могут влиять на исследуемый процесс. При этом используется, как правило, метод последовательного развертывания и детализации параметров. Если при этом окажется, что несколько более сложных параметров в конечном счете могут быть выражены через более простые параметры, то после развертывания и детализации эти более простые параметры войдут в уравнение более одного раза, т.е. повторяться. Тогда освобождаются от повторений, удерживая каждый параметр лишь один раз. Например, если у одного и того же объекта были приняты размеры поперечного сечения a и b, площадь поперечного сечения S и момент инерции I, то в конечном счете можно оставить лишь а и b , a S и I опустить, т.к. последние могут быть выражены через первые. Но возможно и наоборот: сохраняя S и I, опустить а и b . Например, при изучении продольной устойчивости балки (стержня, бурильных труб и т.д.) более важен параметр I, нежели а, b или S. С точки зрения напряженного состояния или прочности конструкции, напротив, может иметь более важное значение S. Иногда бывает необходимо брать не только I, но и более сложный параметр EI – жесткость балки на изгиб. Какие параметры оставить, а от которых необходимо или желательно освободиться, зависит от характера конкретной задачи.

К сожалению, π – теорема не дает ответа на этот вопрос, оставляя поле деятельности для опыта и интуиции исследователя, а также для проб и ошибок.

2 В качестве основных следует выбирать параметры, размерности которых совпадают с размерностями первичных единиц измерения, т.е. имеющие символы [М], [L] и [Т]. Таковыми могут быть масса объекта m, его линейные d, поверхностные S или пространственные V размеры (где d - диаметр, S - площадь, V- объем), а также временная характеристика (например, угловая скорость, частота или период колебаний). Далее идут производные параметры с размерностями в виде комбинаций двух первичных размерностей. Ими могут быть скорость, ускорение, плотность и т.д. Наиболее сложную размерность будут иметь производные параметры, размерности которых представляют собой комбинации всех трех первичных размерностей. Среди них часто встречаются такие параметры, как сила, момент силы, давление, напряжение, вязкость и т.д.

Наиболее легко и просто освободиться от размерностей, когда в качестве основных удается выбрать параметры с самыми простыми размерностями, совпадающими с размерностями первичных величин. Если этого делать не удается, то приходится выбирать параметры с более сложными размерностями. Непременным условием при этом является то, чтобы, во-первых, они в совокупности содержали размерности всех трех первичных величин и, во-

вторых чтобы они были независимы между собой.

Если в качестве основных выбраны параметры с самыми простыми размерностями ([М], [L] и [Т]), то для получения критериев подобия в числитель дроби последовательно записываются все n – r  параметры, а в знаменатель – основные параметры с соответствующими показателями степеней.

В случае, если в качестве основных выбраны параметры с размерностями различной сложности (например, один – в виде одной размерности в какой-либо степени, другой – в виде комбинации двух размерностей, а третий – в виде комбинации всех трех размерностей), то в знаменатель дроби они подставляются в следующей последовательности :

1) если i – й параметр из n – r  оставшихся имеет размерность лишь одной меры измерения, то в знаменатель дроби подставляется тот основной параметр, возведенный в соответствующую степень (целую или дробную), размерность которой совпадает с размерностью i - го параметра;

2) если i - й параметр из n – r параметров по размерности не совпадает c размерностью ни одной из основных единиц, то в знаменатель дроби на каждом этапе подставляют тот параметр, возведенный в соответствующую степень, в размерности которого присутствует элемент размерности i – гo параметра, а этот элемент в размерности других основных единиц отсутствует;

3) наиболее простой параметр следует использовать в последнюю очередь.

Следует отметить, что указанные правила, кажущиеся сложными в формулировках, на самом деле просты при их практическом использовании.

Однако при выборе основных параметров иногда приходится отказаться от некоторых из сформулированных выше правил. Чаще это бывает связано с характером решаемой задачи, стремлением получить уже хорошо известные критерии подобия и т.д.

Покажем вышеизложенное на конкретных (в том числе вышерас-смотренных) примерах.