а) 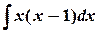 ; б)
; б) 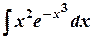 .
.
2) Вычислить определенный интеграл: 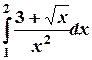
3) Найти общее решение дифференциального уравнения 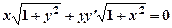 .
.
4) Найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами у // + 16у=0.
5) Написать первые три члена ряда и проверить необходимый признак сходимости для заданного числового ряда 
6) В вазе стоят 8 белых, 7 розовых и 5 красных гвоздик. Наугад берут 4 цветка. Найти вероятность, что все взятые гвоздики красные.
7) Вероятность того, что клиент банка не вернет заем в период экономического роста, равна 0,04, а в период экономического кризиса – 0,13. Предположим, что вероятность того, что начнется период экономического роста, равна 0,65. Зная, что клиент банка не вернул полученный кредит, найти вероятность того, что наблюдается экономический кризис.
8) Задан закон распределения дискретной случайной величины.
| X | 11 | 14 | 17 | 20 | 23 |
| p | 0,2 | 0,3 | 0,25 | 0,15 | 0,1 |
Найти математическое ожидание, дисперсию и с.к.о.
9) Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие нестандартно, равна 0,1. Найти вероятность того, что среди трех проверенных изделий окажется не более одного нестандартного.
10) Зная математическое ожидание т = 11 и среднее квадратичное отклонение s = 4 нормально распределенной случайной величины Х, найти вероятность того, что а) Х примет значение из интервала (13; 23), б) выполнится неравенство |Х – т| < 6.
Вариант 6.
1) Вычислить неопределенные интегралы а)  ; б)
; б) 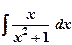 .
.
2) Вычислить определенный интеграл: 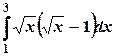 .
.
3) Найти общее решение дифференциального уравнения
y / = ex +у .
4) Найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами
у // - 2у /+2у=0.
5) Написать первые три члена ряда и проверить необходимый признак сходимости для заданного числового ряда 
6) Ребенок играет с буквами разрезной азбуки А, Г, И, К, Н. Найти вероятность того, что при случайном расположении букв в ряд он получит слово «КНИГА».
7) Международная компания обсуждает возможности инвестиций в некоторое государство с неустойчивой политической ситуацией. Менеджеры оценивают вероятность успеха в 0,55, если преобладающая политическая ситуация будет благоприятной; в 0,30, если политическая ситуация будет нейтральной; в 0,10, если политическая ситуация в течение года будет неблагоприятной. Предполагается, что вероятности благоприятной, нейтральной и неблагоприятной политических ситуаций соответственно равны: 0,60, 0,20 и 0,20. Чему равна вероятность успеха инвестиций?
8) Задан закон распределения дискретной случайной величины.
| X | 12 | 14 | 16 | 18 | 20 |
| p | 0,2 | 0,3 | 0,25 | 0,15 | 0,1 |
Найти математическое ожидание, дисперсию и с.к.о.
9) Вероятность того, что в течение гарантийного срока телевизор потребует ремонта, равна 0,2. Найти вероятность того, что в течение гарантийного срока из 6 телевизоров не более одного потребуют ремонта.
10) Зная математическое ожидание т = 10 и среднее квадратичное отклонение s = 8 нормально распределенной случайной величины Х, найти вероятность того, что а) Х примет значение из интервала (14; 18), б) выполнится неравенство |Х – т| < 2.
Вариант 7.
1) Вычислить неопределенные интегралы:
а) 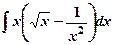 ; б)
; б) 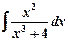 .
.
2) Вычислить определенный интеграл: 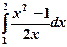
3) Найти общее решение дифференциального уравнения
ey (1+x2) dy – 2x (1+ ey) dx = 0.
4)Найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами
у // + 3у / = 0.
5) Написать первые три члена ряда и проверить необходимый признак сходимости для заданного числового ряда 
6) Из полной колоды карт (52 листа) вынимают сразу четыре карты. Найти вероятность того, что все эти карты будут разных мастей.
7) Два кирпичных завода поставляют одну и ту же марку кирпича на стройку. Первый завод поставляет каждый день 3000 кирпичей, второй – 5000 кирпичей. Известно, что 80% продукции первого завода и 96% продукции второго завода является стандартной. Найти вероятность того, что наугад выбранный из ежедневной поставки кирпич окажется нестандартным?
8) Задан закон распределения дискретной случайной величины.
| X | 1 | 4 | 7 | 10 | 13 |
| p | 0,2 | 0,3 | 0,25 | 0,15 | 0,1 |
Найти математическое ожидание, дисперсию и с.к.о.
9) Вероятность быть принятым на работу в некоторую фирму равна 0,8. Найти вероятность того, что из трех человек, пришедших на собеседование, только двое будут приняты на работу.
10) Зная математическое ожидание т = 9 и среднее квадратичное отклонение s = 3 нормально распределенной случайной величины Х, найти вероятность того, что а) Х примет значение из интервала (9; 18), б) выполнится неравенство |Х – т| < 6.
Вариант 8.
1) Вычислить неопределенные интегралы:
а)  ; б)
; б) 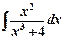 .
.
2) Вычислить определенный интеграл:  ;
;
3) Найти общее решение дифференциального уравнения
ey (1+x2) dy – 2x (1+ ey) dx = 0.
4)Найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами
у // + 3у / = 0.
5) Написать первые три члена ряда и проверить необходимый признак сходимости для заданного числового ряда 
6) Два стрелка сделали по одному выстрелу по мишени. Вероятность попадания для одного из стрелков равна 0,6. Для другого – 0,7. Найти вероятность того, что хотя бы один из стрелков попадет в мишень.
7) При слиянии акционерного капитала двух фирм аналитики фирмы, получающей контрольный пакет акций, полагают, что сделка принесет успех с вероятностью, равной 0,65, если председатель совета директоров поглощаемой фирмы выйдет в отставку; если он откажется, то вероятность успеха будет равна 0,30. Предполагается, что вероятность ухода в отставку председателя составляет 0,70. Чему равна вероятность успеха сделки?
8) Задан закон распределения дискретной случайной величины.
| X | 4 | 6 | 8 | 10 | 12 |
| p | 0,2 | 0,3 | 0,25 | 0,15 | 0,1 |
Найти математическое ожидание, дисперсию и с.к.о.
9) Вероятность попадания в цель при одном выстреле равна 0,2. Сделано 10 выстрелов. Найти вероятность хотя бы одного попадания в цель.
10) Зная математическое ожидание т = 8 и среднее квадратичное отклонение s = 4 нормально распределенной случайной величины Х, найти вероятность того, что а) Х примет значение из интервала (8; 12), б) выполнится неравенство |Х – т| < 8.
Вариант 9.
1) Вычислить неопределенные интегралы: а) 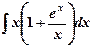 ; б)
; б)  .
.
2)Вычислить определенный интеграл: 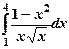 .
.
3) Найти общее решение дифференциального уравнения
(xy2+x) dx + (y– x2y) dy = 0.
4)Найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами у // + у / – 2 y = 0.
5) Написать первые три члена ряда и проверить необходимый признак сходимости для заданного числового ряда 
6) Вероятность, что при нажиме стартера мотор машины заработает, равна примерно 5/6. Найти вероятность того, что мотор включится только при повторном нажиме стартера.
7) Проведя предварительные исследования, нефтеразведчики полагают, что вероятность наличия нефти на проверяемом участке равна 0,4. На завершающем этапе разведки проводится сейсмический тест, который имеет определенную степень надежности: если на проверяемом участке есть нефть, то тест укажет на ее наличие в 85% случаев; если нефти нет, то в 10% случаев тест может ошибочно указать ее присутствие. Сейсмический тест указал на присутствие нефти. Чему равна вероятность того, что запасы нефти на данном участке существуют реально?
8) Задан закон распределения дискретной случайной величины.
| X | – 1 | 2 | 5 | 8 | 11 |
| p | 0,2 | 0,3 | 0,25 | 0,15 | 0,1 |
Найти математическое ожидание, дисперсию и с.к.о.
9) В ящике лежат несколько тысяч одинаковых предохранителей. Половина из них изготовлена первым заводом, остальные – вторым заводом. Наудачу вынули пять предохранителей. Найти вероятность того, что среди них более двух изготовлено первым заводом.
10) Зная математическое ожидание т = 7 и среднее квадратичное отклонение s = 2 нормально распределенной случайной величины Х, найти вероятность того, что а) Х примет значение из интервала (6; 10), б) выполнится неравенство |Х – т| < 4.
Вариант 10.
1) Вычислить неопределенные интегралы а) 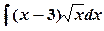 ; б)
; б) 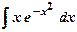 .
.
2) Вычислить определенный интеграл 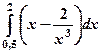 ;
;
3) Найти общее решение дифференциального уравнения (2 y +1) x dx + (1+ x 2 ) dy = 0.
4)Найти общее решение линейного однородного дифференциального
уравнения с постоянными коэффициентами у // - 2у / = 0.
5) Написать первые три члена ряда и проверить необходимый признак сходимости для заданного числового ряда 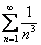
6) Охотник выстрелил три раза по удаляющейся цели. Вероятность попадания в нее в начале стрельбы равна 0,8, а после каждого выстрела уменьшается на 0,1. Найти вероятность того, что он промахнется все три раза.
7) Исследованиями психологов установлено, что мужчины и женщины по-разному реагируют на некоторые жизненные обстоятельства. Результаты исследований показали, что позитивно реагируют на изучаемый круг ситуаций 70% женщин и только 60% мужчин. 15 женщин и 5 мужчин заполнили анкету, в которой отразили свое отношение к предлагаемым ситуациям. Случайно извлеченная анкета содержит негативную реакцию. Чему равна вероятность того, что ее заполнял мужчина?
8) Задан закон распределения дискретной случайной величины.
| X | – 1 | 1 | 3 | 5 | 7 |
| p | 0,2 | 0,3 | 0,25 | 0,15 | 0,1 |
Найти математическое ожидание, дисперсию и с.к.о.
9) Вероятность того, что проверяемое изделие нестандартно, равна 0,1. Найти вероятность того, что из трех проверенных изделий только одно нестандартное.
10) Зная математическое ожидание т = 6 и среднее квадратичное отклонение s = 2 нормально распределенной случайной величины Х, найти вероятность того, что а) Х примет значение из интервала (4; 12), б) выполнится неравенство |Х – т| < 4.
Дата: 2019-05-28, просмотров: 578.