1.1. Определитель 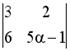 называется определителем
называется определителем
a. первого порядка
b. второго порядка
c. третьего порядка
d. четвертого порядка
1.2. Уравнение  описывает линию с названием
описывает линию с названием
a. гипербола
b. парабола
c. окружность
d. эллипс
1.3. Функция 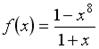 имеет
имеет
a. Одну точку разрыва
b. Две точку разрыва
c. Не имеет точек разрыва
1.4. Произведение данных матриц 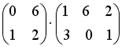 имеет вид матрицы размера
имеет вид матрицы размера
a. 2х2
b. 2х3
c. 3х2
d. 3х3
1.5. Частная производная функции  по переменной
по переменной 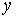 содержит
содержит
a. sin3y
b. siny
c. cos3y
d. cosy
Выбрать Все правильные ответы (больше одного)
1.6. Определитель 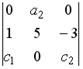 вычисляется
вычисляется
a. по правилу треугольников
b. разложением по первой строке
c. разложением по столбцу
d. по правилу параллелограмма
1.7. Значение предела 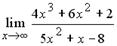 может быть получено
может быть получено
a. вынесением высшей степени в числителе и знаменателе
b. при помощи первого замечательного предела
c. при помощи второго замечательного предела
d. по правилу Лопиталя
1.8. График функции 
a. пересекает ось Х
b. не пересекает ось Х
c. ветви параболы направлены вверх
d. ветви параболы направлены вниз
1.9. При решении системы линейных уравнений с квадратной матрицей коэффициентов 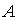 нельзя применять формулы Крамера, если
нельзя применять формулы Крамера, если
a. определитель матрицы 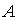 равен нулю
равен нулю
b. строки матрицы 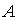 линейно независимы
линейно независимы
c. матрица имеет нулевую строку
d. столбцы матрицы 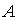 линейно зависимы
линейно зависимы
Заполнить пропуски
1.10. Параболой называется множество всех точек плоскости, для которых расстояние от данной точки, называемой фокусом ______ до данной прямой, называемой директрисой и не проходящей через фокус
a. больше расстояния
b. меньше расстояния
c. не равно расстоянию
d. равно расстоянию
Блок 2 – Проверка умений
2.1.Укажите соответствие между кривыми второго порядка и их уравнениями:
1. 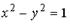
| a. окружность |
2. 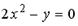
| b. парабола |
3. 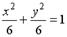
| c. эллипс |
4. 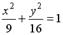
| d. гипербола |
2.2. Вычислить вторую производную для функции 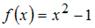
2.3. В экономических задачах часто информация обрабатывается в виде таблиц. Для заданных матриц  и
и 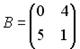 выполнить операцию сложения матриц А+В.
выполнить операцию сложения матриц А+В.
2.4. Пользуясь математической моделью представления информации о распределении и использовании продукции в рамках межотраслевого баланса в макроэкономике X = AX + Y, запишите формулу для нахождения конечного продукта 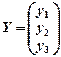 для каждой из трех отраслей
для каждой из трех отраслей
2.5. Укажите соответствие между видом асимптоты и ее уравнением
| 1. y=2 | a. Горизонтальная асимптота |
| 2. x=3 | b. Наклонная асимптота |
| 3. y=2x+2 | c. Вертикальная асимптота |
Блок 3 – Проверка навыков
Время выполнения задания – 30 мин.
3.1. Математический инструментарий процесса выбора потребителя записывается при помощи функций нескольких переменных. Выполнить следующие задания в рамках модели выбора потребителя.
Функция полезности для потребителя двух товаров имеет вид 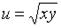 .
.
Записать и изобразить графически бюджетное множество, отражающее покупательные возможности потребителя этих двух товаров, если цена на товар 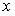 равна 5, на товар
равна 5, на товар 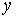 равна 20, доход потребителя равен 200.
равна 20, доход потребителя равен 200.
Найти максимум данной функции полезности при заданном ограничении.
Типовое контрольное задание 2 семестр
Блок 1 – Проверка знаний
Выберите ОДИН вариант ответа
1.1.Закончить утверждение. Ряд называется сходящимся, если
a. Последовательность его частичных сумм имеет конечный или бесконечный предел
b. Предел общего члена ряда равен нулю
c. Последовательность его частичных сумм имеет конечный предел
d. Предел модуля общего члена равен нулю
e. Последовательность его частичных сумм является бесконечно большой
1.2.Дан сходящийся ряд. При отбрасывании нескольких его нулевых членов
a. Ряд остается сходящимся и его сумма не изменяется
b. Ряд остается сходящимся и его сумма изменяется
c. Ряд станет расходящимся
d. Ряд остается сходящимся и его сумма обязательно уменьшится
e. Не зная членов ряда ничего нельзя сказать о сходимости или расходимости нового ряда.
1.3 Неопределенным интегралом называется
a. Совокупность всех производных
b. Совокупность всех первообразных
c. Первообразная функция
1.4 Игральная кость бросается один раз. Тогда вероятность того, что число очков, выпавших на верхней грани, будет больше трех, равна …
a. 
b. 
c. 
d. 1
e.
1.5.Если основная гипотеза имеет вид  : a=10, то конкурирующей может быть гипотеза
: a=10, то конкурирующей может быть гипотеза
a.  : a
: a 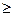 10
10
b.  : a
: a 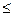 10
10
c.  : a
: a  10
10
d.  : a
: a 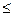 20
20
1.6 Дан закон распределения вероятностей дискретной случайной величины  : : 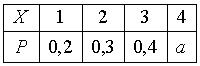 Тогда значение Тогда значение 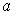 равно
a. -0,7
b. 0,2
c. 0,1
d. 0,7 равно
a. -0,7
b. 0,2
c. 0,1
d. 0,7
|
Выбрать ВСЕ правильные ответы (больше одного)
1.7. 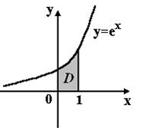
a. При вычислении интеграла по формуле Ньютона-Лейбница, пределы интегрирования равны[0;1]
b. Интеграл вычисляется методом замены переменной
c. Интеграл вычисляется по частям
d. Интеграл вычисляется по таблице
e. Интеграл больше нуля
1.8. Дифференциальное уравнение 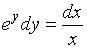
a. первого порядка
b. линейное
c. не линейное
d. с разделяющимися переменными
e. с разделенными переменными
1.9. Среди перечисленных дифференциальных уравнений уравнениями первого порядка являются:
a. 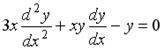
b. 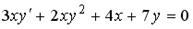
c. 
d. 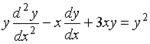
1.10.Из данных рядов выбрать сходящиеся:
a. 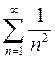
b. 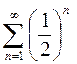
c. 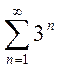
d. 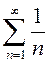
Блок 2 – Проверка умений
2.1. Установить соответствие между левой и правой частью формул таблицы интегралов
1. 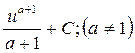
| a. 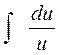
|
2. 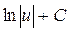
| b. 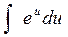
|
3. 
| c. 
|
2.2. Установить соответствие между приведенными дифференциальными уравнениями первого порядка и их типами
1. 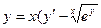
| a. с разделяющими переменными |
2. 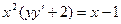
| b. линейное |
3. 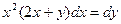
| c. однородное |
2.3. Найти соответствие между числовыми рядами и утверждениями
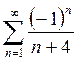
| Общий член ряда не стремится к нулю |

| Знакочередующийся ряд |
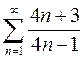
| Гармонический ряд |
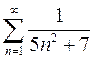
| Сходящийся ряд |
2.4. В результате наблюдений некоторой величины в одних условиях (без систематических ошибок) получены следующие результаты: 12, 14, 16, 18. Найти выборочную несмещенную оценку математического ожидания
2.5. Интервальная оценка математического ожидания нормально распределенного количественного признака X имеет вид (а;25). Найти левую границу доверительного интервала, если выборочная средняя равна 
Блок 3 – Проверка навыков
Дата: 2019-05-28, просмотров: 786.