Вариант 1.
Вычислить интегралы:
1) Вычислить неопределенные интегралы: а) 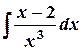 ; б)
; б) 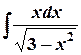
2) Вычислить определенный интеграл 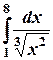 ;
;
3). Найти общее решение дифференциального уравнения
y / (1+ ex ) y = ex .
4) Найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами
у // - 2у /+у=0.
5) Написать первые три члена ряда и проверить необходимый признак сходимости для заданного числового ряда 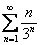
6) Из полного набора домино наугад взяли одну кость. Найти вероятность того, что сумма очков на ней равна 4.
7) Судоходная компания организует средиземноморские круизы в течение летнего времени и проводит несколько круизов в сезон. Чтобы получить прибыль, важно, чтобы все каюты зафрахтованного под круизы корабля были полностью заняты туристами. Эксперт по туризму, нанятый компанией, предсказывает, что корабль будет полон в течение сезона с вероятностью 0,92, если доллар не подорожает по отношению к рублю, и с вероятностью 0,75, если доллар подорожает. По оценкам экономистов, вероятность того, что в течение сезона доллар подорожает по отношению к рублю, равна 0,23. Чему равна вероятность того, что билеты на все круизы будут проданы.
8) Задан закон распределения дискретной случайной величины.
| X | – 4 | – 1 | 2 | 5 | 8 |
| p | 0,2 | 0,3 | 0,25 | 0,15 | 0,1 |
Найти математическое ожидание, дисперсию и с.к.о.
9) Вероятность появления события А при одном испытании равна 0,1. Найти вероятность того, что при трех независимых испытаниях оно появится хотя бы один раз.
10) Зная математическое ожидание т = 15 и среднее квадратичное отклонение s = 2 нормально распределенной случайной величины Х, найти вероятность того, что а) Х примет значение из интервала (9; 19),
б) выполнится неравенство |Х – т| < 3.
Вариант 2.
1) Вычислить неопределенные интегралы:
а)  ; б); в)
; б); в) 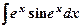 .
.
2) Вычислить определенный интеграл 
а)
3) Найти общее решение дифференциального уравнения
(1+у2) d х + xy d у = 0.
4) Найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами
у // – 4у=0.
5) Написать первые три члена ряда и проверить необходимый признак сходимости для заданного числового ряда 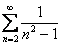
6) При наборе телефонного номера абонент забыл три последние цифры и набрал их наугад, помня только, что эти цифры разные. Найти вероятность того, что номер набран правильно.
7) Два автомата производят одинаковые детали, которые поступают на общий конвейер. Производительность первого автомата вдвое больше производительности второго. Первый автомат производит в среднем 60% деталей отличного качества, а второй – 84% деталей отличного качества. Наудачу взятая с конвейера деталь оказалась отличного качества. Найти вероятность того, что эта деталь изготовлена первым автоматом.
8) Задан закон распределения дискретной случайной величины.
| X | 19 | 21 | 23 | 25 | 27 |
| p | 0,2 | 0,3 | 0,25 | 0,15 | 0,1 |
Найти математическое ожидание, дисперсию и с.к.о.
9) Найти вероятность того, что событие А произойдет не менее двух раз в 4 независимых испытаниях, если вероятность наступления события А в одном испытании равна 0,6.
10) Зная математическое ожидание т = 14 и среднее квадратичное отклонение s = 4 нормально распределенной случайной величины Х, найти вероятность того, что а) Х примет значение из интервала (10; 20), б) выполнится неравенство |Х – т| < 4.
Вариант 3.
1) Вычислить неопределенные интегралы: а) 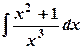 ; б)
; б) 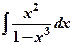 .
.
2) Вычислить определенный интеграл 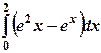
3) Найти общее решение дифференциального уравнения
(1+ x ) y d х + x (1 – y ) d у = 0.
4) Найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами у //+3у /+2у =0.
5) Написать первые три члена ряда и проверить необходимый признак сходимости для заданного числового ряда 
6) В общежитии живут 30 первокурсников, 35 второкурсников, 20 третьекурсников и 15 студентов четвертого курса. Какова вероятность того, что два случайно встреченных студента окажутся с первого курса?
7) Экономист-аналитик условно подразделяет экономическую ситуацию в стране на «хорошую», «посредственную» и «плохую» и оценивает их вероятности для данного момента времени в 0,15; 0,70 и 0,15 соответственно. Некоторый индекс экономического состояния возрастает с вероятностью 0,60, когда ситуация «хорошая»; с вероятностью 0,30, когда ситуация «посредственная», и с вероятностью 0,10, когда ситуация «плохая». Найти вероятность возрастания этого индекса.
8) Задан закон распределения дискретной случайной величины.
| X | 9 | 12 | 15 | 18 | 21 |
| p | 0,2 | 0,3 | 0,25 | 0,15 | 0,1 |
Найти математическое ожидание, дисперсию и с.к.о.
9) В ящике имеется по одинаковому числу деталей, изготовленных заводами №1 и №2. Найти вероятность того, что среди пяти наудачу отобранных деталей менее двух изготовлены на заводе №1.
10). Зная математическое ожидание т = 13 и среднее квадратичное отклонение s = 4 нормально распределенной случайной величины Х, найти вероятность того, что а) Х примет значение из интервала (11; 21), б) выполнится неравенство |Х – т| < 8.
Вариант 4.
1) Вычислить неопределенные интегралы:
а) 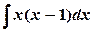 ; б)
; б)  .
.
2) Вычислить определенный интеграл: 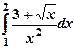 .
.
3) Найти общее решение дифференциального уравнения
 .
.
4) Найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами
у // + 16у=0.
5) Написать первые три члена ряда и проверить необходимый признак сходимости для заданного числового ряда 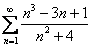
6) Собрание, на котором присутствует 15 человек, в том числе 5 женщин, выбирает делегацию из 3-х человек. Считая, что каждый из присутствующих с одинаковой вероятностью может быть избран, найти
Вероятность того, что в состав делегации войдут две женщины и один мужчина.
7) Из числа авиалиний некоторого аэропорта 60% – местные, 30% – по СНГ и 10% – международные. Среди пассажиров местных авиалиний 50% путешествуют по делам, связанным с бизнесом, на линиях СНГ таких пассажиров 60%, на международных – 90%. Из прибывших в аэропорт пассажиров случайно выбирается один. Чему равна вероятность того, что он бизнесмен?
8) Задан закон распределения дискретной случайной величины.
| X | 0 | 2 | 4 | 6 | 8 |
| p | 0,2 | 0,3 | 0,25 | 0,15 | 0,1 |
Найти математическое ожидание, дисперсию и с.к.о.
9) Вероятность выигрыша по одному билету лотереи равна 0,1. Куплено 4 билета. Найти вероятность того, что выиграет не более одного билета.
10) Зная математическое ожидание т = 12 и среднее квадратичное отклонение s = 5 нормально распределенной случайной величины Х, найти вероятность того, что а) Х примет значение из интервала (12; 22), б) выполнится неравенство |Х – т| < 10.
Вариант 5.
Дата: 2019-05-28, просмотров: 497.