1. Посчитать определитель 4го порядка всеми способами (через миноры).
2. Найти обратную матрицу и выполнить проверку.
3. Решить систему линейных уравнений с квадратной матрицей коэффициентов:
a. Метод определителей (Формулы Крамера)
b. Матричный метод
c. Метод Гаусса
d. Метод Жордана-Гаусса.
4. Решить систему с прямоугольной матрицей коэффициентов (по выбору, углубленный уровень):
a. Найти общее решение, задать его параметрически
b. Найти все базисные решения этой системы.
РГР2 Пределы и непрерывность функций.
Варианты заданий для расчетной работы определяются по порядковому номеру в списке. РГР содержит два задания: на вычисление пределов и на построение графика
1. Найти пределы функций алгебраическими приемами, не пользуясь правилом Лопиталя. (Задачи а и б обязательны для всех. Задачи в и г - на оценку 4 или 5)
1.1. а)  ; б)
; б)  ;
;
в)  ; г)
; г) 
1.2. а)  ; б)
; б) 
в)  ; г)
; г) 
1.3. а);  б)
б) 
в)  ; г)
; г) 
1.4. а)  ; б)
; б) 
в)  ; г)
; г) 
1.5. а)  ; б)
; б) 
в)  ; г)
; г) 
1.6. а)  ; б)
; б) 
в)  ; г)
; г) 
1.7. а)  ; б)
; б) 
в)  ; г)
; г) 
1.8. а)  ; б)
; б) 
в)  ; г)
; г) 
1.9. а)  ; б)
; б) 
в)  ; г)
; г) 
1.10. а)  ; б)
; б) 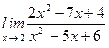
в)  ; г)
; г) 
1.11. а)  ; б)
; б) 
в)  ; г)
; г) 
1.12. а)  ; б)
; б) 
в)  ; г)
; г) 
1.13. а)  ; б)
; б) 
в)  ; г)
; г) 
1.14. а)  ; б)
; б) 
в)  ; г)
; г) 
1.15. а)  ; б)
; б) 
в)  ; г)
; г) 
1.16. а)  ; б)
; б) 
в)  ; г)
; г) 
1.17. а)  ; б)
; б) 
в)  ; г)
; г) 
1.18. а)  ; б)
; б) 
в)  ; г)
; г) 
1.19. а)  ; б)
; б) 
в)  ; г)
; г) 
1.20. а)  ; б)
; б) 
в)  ; г)
; г) 
1.21 а)  ; б)
; б) 
в)  ; г)
; г) 
1.22. а)  ; б)
; б) 
в)  ; г)
; г) 
1.23. а)  ; б)
; б) 
в)  ; г)
; г) 
1.24. а)  ; б)
; б) 
в)  ; г)
; г) 
1.25. а)  ; б)
; б) 
в)  ; г)
; г) 
2.Исследовать данные функции на непрерывность. Функция состоит из нескольких ветвей. Описать ее с точки зрения непрерывности и указать тип разрыва, если он есть. Построить график.
2.1.  ; 2.2.
; 2.2. 
2.3.  ; 2.4.
; 2.4. 
2.5.  ; 2.6.
; 2.6. 
2.7.  ; 2.8.
; 2.8. 
2.9.  ; 2.10.
; 2.10. 
2.11.  ; 2.12.
; 2.12. 
2.13.  ; 2.14.
; 2.14. 
2.15.  ; 2.16.
; 2.16. 
2.17.  ; 2.18.
; 2.18. 
2.19.  ; 2.20.
; 2.20. 
2.21.  2.22.
2.22. 
2.23.  ; 2.24.
; 2.24. 
2.25.  ;
;
Семестр
РГР1 Методы интегрирования
а) вычислить заданный интеграл аналитически, применяя методы интегрирования и таблицу интегралов;
б) вычислить интеграл приближенным методом по формуле трапеций, разбивая отрезок интегрирования на 10 равных частей, а затем на 20 частей (обязательное задание). Сделать графическую иллюстрацию.
Варианты заданий
1) 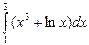 ; 2)
; 2) 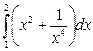 ; 3)
; 3) 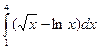 ;
;
4)  ; 5)
; 5)  ; 6)
; 6) 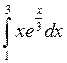 ;
;
7) 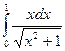 ; 8)
; 8)  ; 9)
; 9) 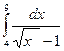 ;
;
10)  ; 11)
; 11) 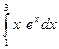 ; 12)
; 12)  ;
;
13) 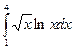 ; 14)
; 14) 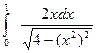 ; 15)
; 15) 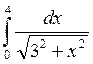 ;
;
16) 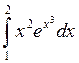 ; 17)
; 17) 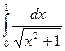 ; 18)
; 18) 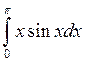 ;
;
19)  ; 20)
; 20)  ; 21)
; 21)  ;
;
22) 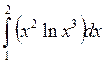 ; 23)
; 23)  ; 24)
; 24) 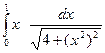 ;
;
25) 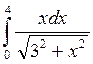 ;
;
РГР2 Элементы теории вероятностей
Варианты заданий для расчетной работы определяются по порядковому номеру студента в списке группы. Буквой V обозначен номер варианта.
Задание к задачам № 1.1 -1.4
1. Переписать текст задачи, заменяя все параметры их значениями для решаемого варианта.
2. Определить испытания и элементарные события.
3. Определить исследуемое событие А и другие события.
4. Установить, какие формулы следует использовать для вычислений и выполнить последние. Вычисления произвести, по возможности, точно.
Задача 1.1. В урне содержится К черных и Н белых шаров. Случайным образом вынимают М шаров. Найти вероятность того, что среди них имеется:
а) Р белых шаров; б) меньше, чем Р, белых шаров;в) хотя бы один белый шар.
Значения параметров К, Н, М и Р по вариантам приведены в табл. 1.
Таблица 1.
| Вариант | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| К | 5 | 5 | 6 | 6 | 7 | 4 | 8 | 6 | 4 | 5 | 7 | 8 | 6 | 4 | 8 | 5 |
| Н | 6 | 6 | 5 | 5 | 4 | 5 | 6 | 7 | 7 | 6 | 4 | 6 | 5 | 6 | 6 | 6 |
| М | 4 | 5 | 4 | 5 | 4 | 4 | 5 | 4 | 4 | 5 | 4 | 4 | 4 | 4 | 5 | 5 |
| Р | 2 | 3 | 2 | 3 | 2 | 2 | 3 | 4 | 2 | 3 | 2 | 3 | 3 | 3 | 2 | 4 |
|
| ||||||||||||||||
| Вариант | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
| К | 7 | 5 | 6 | 5 | 6 | 6 | 6 | 8 | 6 | 5 | 6 | 5 | 6 | 6 | 4 | |
| Н | 4 | 7 | 5 | 7 | 7 | 8 | 5 | 6 | 7 | 7 | 7 | 7 | 8 | 7 | 7 | |
| М | 5 | 4 | 5 | 5 | 5 | 5 | 5 | 5 | 4 | 4 | 6 | 5 | 5 | 5 | 4 | |
| Р | 3 | 3 | 2 | 4 | 3 | 4 | 4 | 3 | 3 | 2 | 3 | 3 | 3 | 2 | 2 | |
Задача 1.2. Устройство состоит из трех независимых элементов, работающих в течение времени Т безотказно соответственно с вероятностями  ,
, 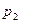 и
и 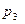 . Найти вероятность того, что за время Т выйдет из строя: а) только один элемент; б) хотя бы один элемент.
. Найти вероятность того, что за время Т выйдет из строя: а) только один элемент; б) хотя бы один элемент.
Значения параметров вычислить по следующим формулам:
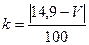 ;
;

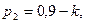
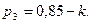
Задача 1.3. В пирамиде стоят R винтовок, из них L, с оптическим прицелом. Стрелок, стреляя из винтовки с оптическим прицелом, может поразить мишень с вероятностью 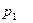 , а, стреляя из винтовки без оптического прицела, — с вероятностью
, а, стреляя из винтовки без оптического прицела, — с вероятностью 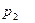 . Найти вероятность того, что стрелок поразит мишень, стреляя из случайно взятой винтовки.
. Найти вероятность того, что стрелок поразит мишень, стреляя из случайно взятой винтовки.
Значения параметров вычислить по следующим формулам:


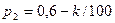
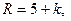
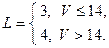
Задача 1.4. В монтажном цехе к устройству присоединяется электродвигатель. Электродвигатели поставляются тремя заводами-изготовителями. На складе имеются электродвигатели этих заводов соответственно в количестве  штук, которые могут безотказно работать до конца гарантийного срока с вероятностями соответственно
штук, которые могут безотказно работать до конца гарантийного срока с вероятностями соответственно 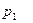 ,
, 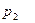 и
и 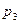 . Рабочий берет случайно один электродвигатель и монтирует его к устройству. Найти вероятности того, что смонтированный и работающий безотказно до конца гарантийного срока электродвигатель поставлен соответственно первым, вторым или третьим заводом-изготовителем.
. Рабочий берет случайно один электродвигатель и монтирует его к устройству. Найти вероятности того, что смонтированный и работающий безотказно до конца гарантийного срока электродвигатель поставлен соответственно первым, вторым или третьим заводом-изготовителем.
Значения параметров вычислить по следующим формулам:

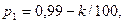
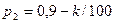

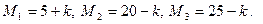
Задание к задачам 1.5 – 1.6.
1) Переписать текст задачи, заменяя все параметры их значениями для решаемого варианта. Определить исходные данные и результаты.
2) Определить подходящие формулы вычисления и выполнить вычисления при помощи микрокалькулятора и таблиц. Построить графики.
Задача 1.5. В каждом из п независимых испытаний событие А происходит с постоянной вероятностью р. Вычислить все вероятности 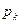 ,
,  , где k — частота события А.
, где k — частота события А.
Построить график вероятностей 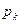 . Найти наивероятнейшую частоту.
. Найти наивероятнейшую частоту.
Значения параметров п и р вычислить по следующим формулам:
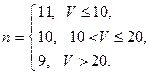

Задача 1.6. В каждом из п независимых испытаний событие А происходит с постоянной вероятностью р. Найти вероятность того, что событие А происходит: а) точно G раз; б) точно L раз; в) меньше чем М и больше чем F раз; г) меньше чем R раз.
Значения параметров п, р, G , L , М, F и R вычислить по следующим формулам:

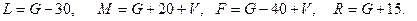
Дата: 2019-05-28, просмотров: 399.