МАТЕМАТИКА
Учебно-методическое пособие
Самара 2017
| УДК 51 | |
| ББК 22.1 | |
|
| |
|
| |
| Математика. Учебно-методическое пособие /Составитель Коваленко Т.Д. – Самара: Университет «МИР», 2017. – 43 с. | |
|
| |
|
| |
| Методическое пособие по дисциплине «Математика» включает содержание тематических разделов дисциплины, материалы для текущего контроля, пример оценочных материалов для промежуточной аттестации. | |
| Методическое пособие предназначено для студентов, обучающихся по направлению «Менеджмент», профили «Маркетинг» и «Менеджмент организации». | |
| Составитель: | Коваленко Татьяна Дмитриевна |
| к.т.н., доцент | |
| Рецензент: | Горбунова Оксана Александровна |
| к.э.н., доцент | |
| Печатается по решению Учебно-методического совета АНО ВО Университета «МИР» | |
| © АНО ВО Университет «МИР», 2017 | |
| © Составление: Коваленко Т.Д., 2017 | |
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ .. 4
СОДЕРЖАНИЕ ТЕМАТИЧЕСКИХ РАЗДЕЛОВ ДИСЦИПЛИНЫ ... 4
ПЕРЕЧЕНЬ УЧЕБНО-МЕТОДИЧЕСКОГО И ИНФОРМАЦИОННОГО ОБЕСПЕЧЕНИЯ ДИСЦИПЛИНЫ ... 6
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ПРЕПОДАВАТЕЛЯ .. 6
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ СТУДЕНТОВ .. 9
ФОНД ОЦЕНОЧНЫХ СРЕДСТВ (для проведения экзамена) 10
Материалы для текущего контроля .. 17
Образцы контрольных работ очной формы обучения . 17
Семестр . 17
КР1. Линейная алгебра и элементы аналитической геометрии . 17
КР2. Применение производных . 18
Семестр . 18
КР1. Интегралы, дифференциальные уравнения . 18
КР2. Основы теории вероятностей . 19
Оценочные средства для внеаудиторной работы в виде расчетно-графических работ . 21
Семестр . 21
РГР1
РГР2
Семестр . 25
РГР1 . 25
РГР2 26
Варианты заданий контрольной работы для заочной формы обучения . 28
Контрольная работа №1 первый семестр . 28
Контрольная работа №2 второй семестр . 35
ВВЕДЕНИЕ
Цель курса: приобретение твердых навыков решения математических задач, математического моделирования, освоение методологии математического мышления. Формирование логического мышления, навыков математического исследования прикладных вопросов, самостоятельной постановки математических задач и анализа разработанных моделей и поиска оптимальных решений актуальных практических задач, самостоятельного изучения литературы по математике.
Задачи курса:
- развитие математической культуры для количественного анализа социально-экономических процессов;
- формирование навыков самостоятельной работы, необходимых при изучении специальных дисциплин и дальнейшей практической деятельности;
- овладение необходимым математическим аппаратом, помогающим анализировать, моделировать и решать прикладные управленческие задачи;
- выработка навыков применения аналитических и численных методов решения стандартных задач, лежащих в основе математических моделей социально-экономических процессов;
- развитие аналитических способностей и навыков самостоятельного количественного анализа для успешного изучения специальных дисциплин.
СОДЕРЖАНИЕ ТЕМАТИЧЕСКИХ РАЗДЕЛОВ ДИСЦИПЛИНЫ
| Наименование раздела | Содержание раздела |
| Введение в дисциплину | Применение понятий и категорий и методов математики для получения и обработки информации в соответствии с поставленной задачей. Количественное описание процессов с использованием числовых множеств и таблиц. Качественное описание процессов с использованием функций и критериальных значений в виде неравенств. |
| Основные алгебраические структуры линейной алгебры. Матрицы и определители. | Матрица как инструмент табличного представления и обработки деловой информации. Матрицы, линейные операции над матрицами, умножение матриц. Квадратные матрицы, их определители. Схемы вычисления определителей второго и третьего порядков. Миноры и алгебраические дополнения элементов определителя. Теоремы о разложении определителя по элементам строк (столбцов). Понятие о ранге матрицы. Обратная матрица, ее вычисление. |
| Системы линейных алгебраических уравнений | Системы линейных алгебраических уравнений (СЛАУ), различные формы их записи. Понятие решения СЛАУ, совместные, несовместные, определенные, неопределенные СЛАУ. Правило Крамера для решения СЛАУ. Матричный метод решения СЛАУ. Примеры задач экономического содержания, приводящих к решению СЛАУ. Элементарные преобразования, сохраняющие равносильность. Метод Жордана-Гаусса (полного исключения неизвестных) для решения СЛАУ. Примеры. Общее, частные и базисные решения СЛАУ. Однородные линейные системы. Системы с прямоугольной матрицей коэффициентов. Геометрический смысл линейных уравнений и неравенств. |
| Элементы аналитической геометрии. | Вектор на плоскости и в пространстве. Разложение вектора на составляющие в декартовом базисе. Длина вектора. Линейные операции над векторами. Скалярное произведение векторов. Приложения скалярного произведения. Условие коллинеарности и ортогональности векторов. Применение векторов в экономических исследованиях. Векторное и смешанное произведения векторов. Общее уравнение плоскости и канонические уравнения прямой в трехмерном пространстве, их частные случаи. Взаимное положение в пространстве. Канонические линии второго порядка |
| Введение в анализ. Функция как основной вид математической модели. Пределы и непрерывность | Числовые множества, числовая ось, окрестность точки. Определение функции, способы ее задания. Основные элементарные функции, их свойства и графики (обзор). Применение функции в качестве инструмента обработки информации об экономических данных. Определение предела функции в точке и на бесконечности. Бесконечно-малые и бесконечно-большие функции, их свойства и взаимная связь. Основные теоремы о пределах. Виды неопределенностей и способы их раскрытия. Непрерывность функции в точке. Точки разрыва, их виды. Теоремы о непрерывных функциях, непрерывность элементарных функций. Свойства функций, непрерывных на отрезке |
| Дифференциальное исчисление функции одной действительной переменной | Понятие производной, ее геометрический, механический и экономический смысл. Дифференциал функции, его геометрический смысл. Связь непрерывности и дифференцируемости функции. Формулы дифференцирования основных элементарных функций. Правила дифференцирования суммы, разности, произведения, частного и суперпозиции функций. Производные высших порядков. Правило Лопиталя. Признаки монотонности функции. Понятие экстремумов, необходимые и достаточные условия экстремумов. Правило исследования функции на экстремум. Признаки выпуклости и вогнутости функции, условия перегиба. П Асимптоты функции, их виды и нахождение. Общая схема полного исследования функции. Анализ графиков функций. Глобальные экстремумы, правило их нахождения. Приложения производной в экономических задачах |
| Функции нескольких переменных | Понятие ФНП, область определения ФНП. На примере функции 2х переменных. Определение частных производных первого порядка. Дифференциал (полная производная) функции нескольких переменных. Производная вдоль вектора и по направлению. Градиент и его свойства. Частные производные и дифференциалы высших порядков. Формула Тейлора для функции нескольких переменных (без доказательства). Определение локальных экстремумов функций нескольких переменных. Необходимое условие экстремума. Достаточное условие экстремума. Условный экстремум. |
| Неопределенный интеграл. Определенный интеграл. Несобственные интегралы | Первообразная функция. Неопределенный интеграл, его свойства. Таблица интегралов. Существование неопределенного интеграла. Интегрирование в элементарных функциях. Методы интегрирования: непосредственное, замена переменной, интегрирование по частям. Интегрирование некоторых классов функции: рациональных дробей. Определенный интеграл как предел интегральной суммы, его основные свойства. Формула Ньютона-Лейбница для вычисления определенного интеграла. Методы интегрирования заменой переменной и по частям в определенном интеграле. Приложения интеграла к вычислению площадей плоских фигур. Использование определенного интеграла в экономике. Несобственные интегралы с бесконечными пределами интегрирования. |
| Простейшие типы дифференциальных уравнений. Основные понятия и применение числовых рядов | Понятие дифференциального уравнения и его решения. Дифференциальное уравнение первого порядка, его общее, частное и особое решения, их геометрический смысл. Задача Коши, теорема о существовании и единственности ее решения. Дифференциальные уравнения с разделяющимися переменными. Линейные дифференциальные уравнения первого порядка. Примеры решения дифференциальных уравнений из области экономики. Понятие числового ряда, сходимость, простейшие признаки сходимости. |
| Теория вероятностей как инструмент обработки информации в соответствии с поставленной задачей | Основные понятия теории вероятностей, случайные события и операции над ними. Классическое, геометрическое, статистическое определения вероятности. Теоремы сложения и умножения вероятностей.Условная вероятность. Полная группа событий. Формулы полной вероятности и Байеса. Схема независимых испытаний Бернулли. Обобщение схемы Бернулли, формула Пуассона, локальная и интегральная теоремы Муавра-Лапласа. Случайные величины и законы распределения. Дискретные и непрерывные случайные величины. Числовые характеристики случайных величин, их свойства. Особая роль математического ожидания и дисперсии при обработке и анализе деловой информации и экономических данных и его свойства. Законы распределения часто применимые в экономике. Особая роль нормального закона, кривая ошибок Гаусса, функция распределения. Функция Лапласа. Двумерные случайные величины. Корреляция и регрессия. |
| Элементы математической статистики | Математическая статистика. Основные понятия и задачи математической статистики. Генеральная совокупность, выборка. Эмпирическая функция распределения. Точечные оценки параметров распределений, их свойства: состоятельность, несмещённость, эффективность. Интервальные оценки, доверительная вероятность. Статистические гипотезы. Проверка статистических гипотез. Примеры критериев проверки параметрических гипотез. |
ПЕРЕЧЕНЬ УЧЕБНО-МЕТОДИЧЕСКОГО И ИНФОРМАЦИОННОГО ОБЕСПЕЧЕНИЯ ДИСЦИПЛИНЫ
Учебная литература, в том числе:
Основная:
1. Высшая математика для экономистов : учебник / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман ; под ред. Н.Ш. Кремера. - 3-е изд. - Москва : Юнити-Дана, 2015. - 482 с. : граф. - («Золотой фонд российских учебников»). - ISBN 978-5-238-00991-9 ; То же [Электронный ресурс]. - URL: http://biblioclub.ru/index.php?page=book&id=114541
2. Краткий курс высшей математики : учебник / К.В. Балдин, Ф.К. Балдин, В.И. Джеффаль и др. ; под общ. ред. К.В. Балдина. - 2-е изд. - Москва : Издательско-торговая корпорация «Дашков и К°», 2017. - 512 с. : табл., граф., схем., ил. - Библиогр. в кн. - ISBN 978-5-394-02103-9 ; То же [Электронный ресурс]. - URL: http://biblioclub.ru/index.php?page=book&id=450751
3. Кузнецов, Б.Т. Математика : учебник / Б.Т. Кузнецов. - 2-е изд., перераб. и доп. - Москва : Юнити-Дана, 2015. - 719 с. : ил., табл., граф. - (Высшее профессиональное образование: Экономика и управление). - Библиогр. в кн. - ISBN 5-238-00754-Х ; То же [Электронный ресурс]. - URL: http://biblioclub.ru/index.php?page=book&id=114717
4. Никонова, Н.В. Краткий курс алгебры и геометрии: примеры, задачи, тесты : учебное пособие / Н.В. Никонова, Н.Н. Газизова, Г.А. Никонова ; Министерство образования и науки России, Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Казанский национальный исследовательский технологический университет». - Казань : Издательство КНИТУ, 2014. - 100 с. : ил. - Библиогр. в кн. - ISBN 978-5-7882-1711-6 ; То же [Электронный ресурс]. - URL: http://biblioclub.ru/index.php?page=book&id=428767
5. Яновский, А.А. Дифференциальное исчисление функции одной переменной : учебное пособие / А.А. Яновский ; Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Ставропольский государственный аграрный университет. - Ставрополь : Ставропольский государственный аграрный университет, 2015. - 50 с. : табл., граф. - Библиогр. в кн. ; То же [Электронный ресурс]. - URL: http://biblioclub.ru/index.php?page=book&id=438875
Дополнительная:
1. Маталыцкий, М.А. Теория вероятностей и математическая статистика : учебник / М.А. Маталыцкий, Г.А. Хацкевич. - Минск : Вышэйшая школа, 2017. - 592 с. - Библиогр. в кн. - ISBN 978-985-06-2855-8 ; То же [Электронный ресурс]. - URL: http://biblioclub.ru/index.php?page=book&id=477424
2. Никонова, Н.В. Краткий курс алгебры и геометрии: примеры, задачи, тесты : учебное пособие / Н.В. Никонова, Н.Н. Газизова, Г.А. Никонова ; Министерство образования и науки России, Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Казанский национальный исследовательский технологический университет». - Казань : Издательство КНИТУ, 2014. - 100 с. : ил. - Библиогр. в кн. - ISBN 978-5-7882-1711-6 ; То же [Электронный ресурс]. - URL: http://biblioclub.ru/index.php?page=book&id=428767
3. Новосельцева, М.А. Теория вероятностей и математическая статистика : учебное пособие / М.А. Новосельцева ; Министерство образования и науки Российской Федерации, Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Кемеровский государственный университет», Кафедра автоматизации исследований и технической кибернетики. - Кемерово : Кемеровский государственный университет, 2014. - 104 с. : ил. - Библиогр. в кн. - ISBN 978-5-8353-1764-6 ; То же [Электронный ресурс]. - URL: http://biblioclub.ru/index.php?page=book&id=278497
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ СТУДЕНТОВ
Для успешного освоения дисциплины студенты должны посещать лекционные занятия, готовиться и активно участвовать в практических занятиях, самостоятельно работать с рекомендованной литературой. Изучение дисциплины целесообразно начать со знакомства с программой курса, чтобы четко представить себе объем и основные проблемы курса. Прочитав соответствующий раздел программы, и установив круг тем, подлежащих изучению, можно переходить к работе с конспектами лекций и учебником. Конспект лекций должен содержать краткое изложение основных вопросов курса. В лекциях преподаватель, как правило, выделяет выводы, содержащиеся в новейших исследованиях, разногласия ученых, обосновывает наиболее убедительную точку зрения. Необходимо записывать методические советы преподавателя, названия рекомендуемых им изданий. Не нужно стремиться к дословной записи лекций. Для того чтобы выделить главное в лекции и правильно ее законспектировать, полезно заранее просмотреть уже пройденный лекционный материал, для более полного и эффективного восприятия новой информации в контексте уже имеющихся знаний, приготовить вопросы лектору. Прочитав свой конспект лекций, следует обратиться к материалу учебника.
Обращение к ранее изученному материалу не только помогает восстановить в памяти известные положения, выводы, но и приводит разрозненные знания в систему, углубляет и расширяет их. Каждый возврат к пройденному материалу позволяет найти в нем что-то новое, переосмыслить его с иных позиций, определить для него наиболее подходящее место в уже имеющейся системе знаний. Неоднократное обращение к пройденному материалу является наиболее рациональной формой приобретения и закрепления знаний. Очень полезным в практике самостоятельной работы является предварительное ознакомление с учебным материалом. Даже краткое, беглое знакомство с материалом очередной лекции дает многое. Студенты получают общее представление о ее содержании и структуре, о главных и второстепенных вопросах, о терминах и определениях. Все это облегчает работу на лекции и делает ее целеустремленной.
Работа с литературой
При изучении дисциплины студенты должны серьезно подойти к исследованию основной и дополнительной литературы. Данное требование особенно важно для подготовки к практическим занятиям.
Особое внимание студентам следует обратить на соответствующие статьи из научных журналов. Данные периодические издания представлены в читальном зале Университета. Для поиска научной литературы по дисциплине студентам также следует использовать каталог Электронной научной библиотеки: eLIBRARY.RU, ЭБС «Университетская библиотека Online».
При подготовке к практическому занятию студенты имеют возможность воспользоваться консультациями преподавателя. Качество учебной работы студентов определяется текущим контролем. Студент имеет право ознакомиться с ним.
Методические рекомендации по самостоятельной работе студентов
Цель самостоятельной работы - подготовка современного компетентного специалиста и формирование способностей и навыков к непрерывному самообразованию и профессиональному совершенствованию.
Реализация поставленной цели предполагает решение следующих задач:
- качественное освоение теоретического материала по изучаемой дисциплине, углубление и расширение теоретических знаний с целью их применения на уровне межпредметных связей;
- систематизация и закрепление полученных теоретических знаний и практических навыков;
- формирование умений по поиску и использованию нормативной, правовой, справочной и специальной литературы, а также других источников информации;
- развитие познавательных способностей и активности, творческой инициативы, самостоятельности, ответственности и организованности;
- формирование самостоятельности мышления, способностей к саморазвитию, самообразованию, самосовершенствованию и самореализации;
- развитие научно-исследовательских навыков;
- формирование умения решать практические задачи (в профессиональной деятельности), используя приобретенные знания, способности и навыки.
Самостоятельная работа является неотъемлемой частью образовательного процесса.
Самостоятельная работа предполагает инициативу самого обучающегося в процессе сбора и усвоения информации, приобретения новых знаний, умений и навыков и ответственность его за планирование, реализацию и оценку результатов учебной деятельности. Процесс освоения знаний при самостоятельной работе не обособлен от других форм обучения.
Самостоятельная работа должна:
- быть выполнена индивидуально (или являться частью коллективной работы). В случае, когда самостоятельная работа подготовлена в порядке выполнения группового задания, в работе делается соответствующая оговорка;
- представлять собой законченную разработку (этап разработки), в которой анализируются актуальные проблемы по определенной теме и ее отдельных аспектов;
- отражать необходимую и достаточную компетентность автора;
- иметь учебную, научную и/или практическую направленность;
- быть оформлена структурно и в логической последовательности: титульный лист, оглавление, основная часть, заключение, выводы, список литературы, приложения;
- содержать краткие и четкие формулировки, убедительную аргументацию, доказательность и обоснованность выводов;
- соответствовать этическим нормам (правила цитирования и парафраз; ссылки на использованные библиографические источники; исключение плагиата, дублирования собственного текста и использования чужих работ).
ФОНД ОЦЕНОЧНЫХ СРЕДСТВ (для проведения экзамена)
Типовое контрольное задание 1 семестр
Блок 1 – Проверка знаний
Заполнить пропуски
1.10. Параболой называется множество всех точек плоскости, для которых расстояние от данной точки, называемой фокусом ______ до данной прямой, называемой директрисой и не проходящей через фокус
a. больше расстояния
b. меньше расстояния
c. не равно расстоянию
d. равно расстоянию
Блок 2 – Проверка умений
2.1.Укажите соответствие между кривыми второго порядка и их уравнениями:
1. 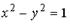
| a. окружность |
2. 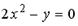
| b. парабола |
3. 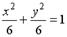
| c. эллипс |
4. 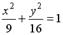
| d. гипербола |
2.2. Вычислить вторую производную для функции 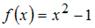
2.3. В экономических задачах часто информация обрабатывается в виде таблиц. Для заданных матриц  и
и 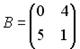 выполнить операцию сложения матриц А+В.
выполнить операцию сложения матриц А+В.
2.4. Пользуясь математической моделью представления информации о распределении и использовании продукции в рамках межотраслевого баланса в макроэкономике X = AX + Y, запишите формулу для нахождения конечного продукта 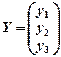 для каждой из трех отраслей
для каждой из трех отраслей
2.5. Укажите соответствие между видом асимптоты и ее уравнением
| 1. y=2 | a. Горизонтальная асимптота |
| 2. x=3 | b. Наклонная асимптота |
| 3. y=2x+2 | c. Вертикальная асимптота |
Блок 3 – Проверка навыков
Время выполнения задания – 30 мин.
3.1. Математический инструментарий процесса выбора потребителя записывается при помощи функций нескольких переменных. Выполнить следующие задания в рамках модели выбора потребителя.
Функция полезности для потребителя двух товаров имеет вид 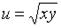 .
.
Записать и изобразить графически бюджетное множество, отражающее покупательные возможности потребителя этих двух товаров, если цена на товар 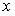 равна 5, на товар
равна 5, на товар 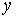 равна 20, доход потребителя равен 200.
равна 20, доход потребителя равен 200.
Найти максимум данной функции полезности при заданном ограничении.
Типовое контрольное задание 2 семестр
Блок 1 – Проверка знаний
Выберите ОДИН вариант ответа
1.1.Закончить утверждение. Ряд называется сходящимся, если
a. Последовательность его частичных сумм имеет конечный или бесконечный предел
b. Предел общего члена ряда равен нулю
c. Последовательность его частичных сумм имеет конечный предел
d. Предел модуля общего члена равен нулю
e. Последовательность его частичных сумм является бесконечно большой
1.2.Дан сходящийся ряд. При отбрасывании нескольких его нулевых членов
a. Ряд остается сходящимся и его сумма не изменяется
b. Ряд остается сходящимся и его сумма изменяется
c. Ряд станет расходящимся
d. Ряд остается сходящимся и его сумма обязательно уменьшится
e. Не зная членов ряда ничего нельзя сказать о сходимости или расходимости нового ряда.
1.3 Неопределенным интегралом называется
a. Совокупность всех производных
b. Совокупность всех первообразных
c. Первообразная функция
1.4 Игральная кость бросается один раз. Тогда вероятность того, что число очков, выпавших на верхней грани, будет больше трех, равна …
a. 
b. 
c. 
d. 1
e.
1.5.Если основная гипотеза имеет вид  : a=10, то конкурирующей может быть гипотеза
: a=10, то конкурирующей может быть гипотеза
a.  : a
: a 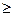 10
10
b.  : a
: a 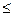 10
10
c.  : a
: a  10
10
d.  : a
: a 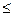 20
20
1.6 Дан закон распределения вероятностей дискретной случайной величины  : : 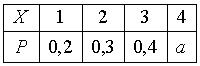 Тогда значение Тогда значение 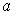 равно
a. -0,7
b. 0,2
c. 0,1
d. 0,7 равно
a. -0,7
b. 0,2
c. 0,1
d. 0,7
|
Выбрать ВСЕ правильные ответы (больше одного)
1.7. 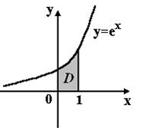
a. При вычислении интеграла по формуле Ньютона-Лейбница, пределы интегрирования равны[0;1]
b. Интеграл вычисляется методом замены переменной
c. Интеграл вычисляется по частям
d. Интеграл вычисляется по таблице
e. Интеграл больше нуля
1.8. Дифференциальное уравнение 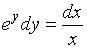
a. первого порядка
b. линейное
c. не линейное
d. с разделяющимися переменными
e. с разделенными переменными
1.9. Среди перечисленных дифференциальных уравнений уравнениями первого порядка являются:
a. 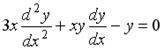
b. 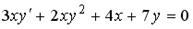
c. 
d. 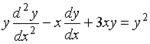
1.10.Из данных рядов выбрать сходящиеся:
a. 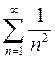
b. 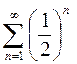
c. 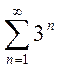
d. 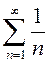
Блок 2 – Проверка умений
2.1. Установить соответствие между левой и правой частью формул таблицы интегралов
1. 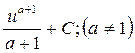
| a. 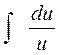
|
2. 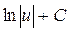
| b. 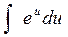
|
3. 
| c. 
|
2.2. Установить соответствие между приведенными дифференциальными уравнениями первого порядка и их типами
1. 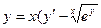
| a. с разделяющими переменными |
2. 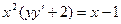
| b. линейное |
3. 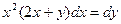
| c. однородное |
2.3. Найти соответствие между числовыми рядами и утверждениями
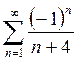
| Общий член ряда не стремится к нулю |

| Знакочередующийся ряд |
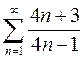
| Гармонический ряд |
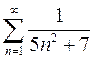
| Сходящийся ряд |
2.4. В результате наблюдений некоторой величины в одних условиях (без систематических ошибок) получены следующие результаты: 12, 14, 16, 18. Найти выборочную несмещенную оценку математического ожидания
2.5. Интервальная оценка математического ожидания нормально распределенного количественного признака X имеет вид (а;25). Найти левую границу доверительного интервала, если выборочная средняя равна 
Блок 3 – Проверка навыков
Семестр
КР2. Применение производных
1. Для функции 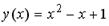 в точке
в точке 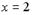 задано приращение аргумента
задано приращение аргумента  Найти соответствующее приращение функции
Найти соответствующее приращение функции 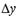
2. Найти все точки экстремума и точки перегиба для функции у=2х3+3х2–4
3. а. Вычислить производную сложной функции 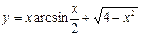
b. Вычислить значение третьей производной функции  в точке х=е.
в точке х=е.
4. Найти и выразить производную неявно заданной функции 
5. Вычислить предел по правилу Лопиталя 
Семестр
Семестр
Семестр
РГР1 Методы интегрирования
а) вычислить заданный интеграл аналитически, применяя методы интегрирования и таблицу интегралов;
б) вычислить интеграл приближенным методом по формуле трапеций, разбивая отрезок интегрирования на 10 равных частей, а затем на 20 частей (обязательное задание). Сделать графическую иллюстрацию.
Варианты заданий
1) 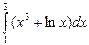 ; 2)
; 2) 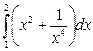 ; 3)
; 3) 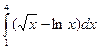 ;
;
4)  ; 5)
; 5)  ; 6)
; 6) 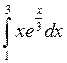 ;
;
7) 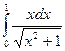 ; 8)
; 8)  ; 9)
; 9) 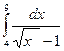 ;
;
10)  ; 11)
; 11) 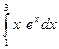 ; 12)
; 12)  ;
;
13) 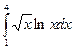 ; 14)
; 14) 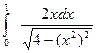 ; 15)
; 15) 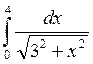 ;
;
16) 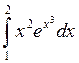 ; 17)
; 17) 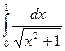 ; 18)
; 18) 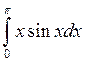 ;
;
19)  ; 20)
; 20)  ; 21)
; 21)  ;
;
22) 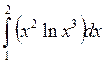 ; 23)
; 23)  ; 24)
; 24) 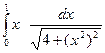 ;
;
25) 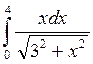 ;
;
Задание к задачам № 1.1 -1.4
1. Переписать текст задачи, заменяя все параметры их значениями для решаемого варианта.
2. Определить испытания и элементарные события.
3. Определить исследуемое событие А и другие события.
4. Установить, какие формулы следует использовать для вычислений и выполнить последние. Вычисления произвести, по возможности, точно.
Задача 1.1. В урне содержится К черных и Н белых шаров. Случайным образом вынимают М шаров. Найти вероятность того, что среди них имеется:
а) Р белых шаров; б) меньше, чем Р, белых шаров;в) хотя бы один белый шар.
Значения параметров К, Н, М и Р по вариантам приведены в табл. 1.
Таблица 1.
| Вариант | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| К | 5 | 5 | 6 | 6 | 7 | 4 | 8 | 6 | 4 | 5 | 7 | 8 | 6 | 4 | 8 | 5 |
| Н | 6 | 6 | 5 | 5 | 4 | 5 | 6 | 7 | 7 | 6 | 4 | 6 | 5 | 6 | 6 | 6 |
| М | 4 | 5 | 4 | 5 | 4 | 4 | 5 | 4 | 4 | 5 | 4 | 4 | 4 | 4 | 5 | 5 |
| Р | 2 | 3 | 2 | 3 | 2 | 2 | 3 | 4 | 2 | 3 | 2 | 3 | 3 | 3 | 2 | 4 |
|
| ||||||||||||||||
| Вариант | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
| К | 7 | 5 | 6 | 5 | 6 | 6 | 6 | 8 | 6 | 5 | 6 | 5 | 6 | 6 | 4 | |
| Н | 4 | 7 | 5 | 7 | 7 | 8 | 5 | 6 | 7 | 7 | 7 | 7 | 8 | 7 | 7 | |
| М | 5 | 4 | 5 | 5 | 5 | 5 | 5 | 5 | 4 | 4 | 6 | 5 | 5 | 5 | 4 | |
| Р | 3 | 3 | 2 | 4 | 3 | 4 | 4 | 3 | 3 | 2 | 3 | 3 | 3 | 2 | 2 | |
Задача 1.2. Устройство состоит из трех независимых элементов, работающих в течение времени Т безотказно соответственно с вероятностями  ,
, 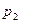 и
и 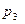 . Найти вероятность того, что за время Т выйдет из строя: а) только один элемент; б) хотя бы один элемент.
. Найти вероятность того, что за время Т выйдет из строя: а) только один элемент; б) хотя бы один элемент.
Значения параметров вычислить по следующим формулам:
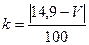 ;
;

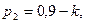
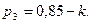
Задача 1.3. В пирамиде стоят R винтовок, из них L, с оптическим прицелом. Стрелок, стреляя из винтовки с оптическим прицелом, может поразить мишень с вероятностью 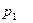 , а, стреляя из винтовки без оптического прицела, — с вероятностью
, а, стреляя из винтовки без оптического прицела, — с вероятностью 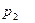 . Найти вероятность того, что стрелок поразит мишень, стреляя из случайно взятой винтовки.
. Найти вероятность того, что стрелок поразит мишень, стреляя из случайно взятой винтовки.
Значения параметров вычислить по следующим формулам:


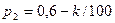
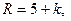
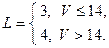
Задача 1.4. В монтажном цехе к устройству присоединяется электродвигатель. Электродвигатели поставляются тремя заводами-изготовителями. На складе имеются электродвигатели этих заводов соответственно в количестве  штук, которые могут безотказно работать до конца гарантийного срока с вероятностями соответственно
штук, которые могут безотказно работать до конца гарантийного срока с вероятностями соответственно 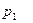 ,
, 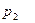 и
и 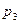 . Рабочий берет случайно один электродвигатель и монтирует его к устройству. Найти вероятности того, что смонтированный и работающий безотказно до конца гарантийного срока электродвигатель поставлен соответственно первым, вторым или третьим заводом-изготовителем.
. Рабочий берет случайно один электродвигатель и монтирует его к устройству. Найти вероятности того, что смонтированный и работающий безотказно до конца гарантийного срока электродвигатель поставлен соответственно первым, вторым или третьим заводом-изготовителем.
Значения параметров вычислить по следующим формулам:

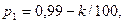
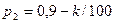

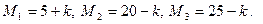
Задание к задачам 1.5 – 1.6.
1) Переписать текст задачи, заменяя все параметры их значениями для решаемого варианта. Определить исходные данные и результаты.
2) Определить подходящие формулы вычисления и выполнить вычисления при помощи микрокалькулятора и таблиц. Построить графики.
Задача 1.5. В каждом из п независимых испытаний событие А происходит с постоянной вероятностью р. Вычислить все вероятности 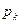 ,
,  , где k — частота события А.
, где k — частота события А.
Построить график вероятностей 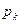 . Найти наивероятнейшую частоту.
. Найти наивероятнейшую частоту.
Значения параметров п и р вычислить по следующим формулам:
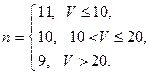

Задача 1.6. В каждом из п независимых испытаний событие А происходит с постоянной вероятностью р. Найти вероятность того, что событие А происходит: а) точно G раз; б) точно L раз; в) меньше чем М и больше чем F раз; г) меньше чем R раз.
Значения параметров п, р, G , L , М, F и R вычислить по следующим формулам:

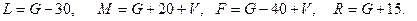
Варианты заданий контрольной работы для заочной формы обучения
Вариант 1.
1) Решить систему уравнений по формулам определителей Крамера. Сделать проверку.
x + 2 y + 3 z = 9 ,
2 x + 3 y + z = 4 ,
3 x – y – 2 z = 1 .
2) Записать матричное уравнение в виде системы линейных уравнений и решить методом Гаусса. Сделать проверку.
(х1 х2 х3)  = (0 0 0).
= (0 0 0).
3) Пользуясь геометрическим смыслом системы линейных неравенств, построить бюджетное множество, отражающее покупательные возможности потребителя двух товаров по цене 75 и 50 руб., если на их приобретение можно израсходовать не более 3000 руб. и второго товара требуется не менее 15 единиц.
4) Вычислить определитель, составленный из координат векторов и выяснить, какая из систем векторов линейно независима. Разложить по ней вектор р = (3; 2; 1):
а) а1 = (1; 3; 0); а2 = (1; -1; 2); а3 = (1/2; 3; -3/4);
б) b 1 = (2; 1; 0); b 2 = (3; 0; -1); b 3 = (0; 3; 4).
5) Вычислить пределы:
а) 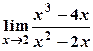 ; б)
; б) 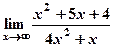 .
.
6) Найти производную функции (y/x) и вычислить ее значение при x = 1:
а) y = x2 lnx ; б) 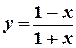 ; в) x 3 + xy + y 2 =3 .
; в) x 3 + xy + y 2 =3 .
7) Исследовать функцию у =2х3+3х2–1 и построить ее график.
8) Изобразить на плоскости xOy область определения функции двух переменных 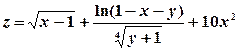 .
.
9) Найти  , если
, если 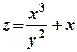 .
.
10) Найти стационарные точки и исследовать на экстремум функцию
z = x 2 – xy + y 2 + 9 x – 6 y + 20 .
Вариант 2.
1) Решить систему уравнений. Сделать проверку.
x + 3 y + 2 z = 4 ,
3 x + 2 y + z = 9 ,
2 x – y – 3 z = 1 .
2) Записать в виде системы линейных уравнений и решить эту систему методом Гаусса. Сделать проверку.
(х1 х2 х3) 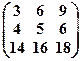 = (0 0 0).
= (0 0 0).
3) Построить бюджетное множество, отражающее покупательные возможности потребителя двух товаров по цене 175 и 70 руб., если на их приобретение можно израсходовать не более 3500 руб. а первого товара имеется не более 15 единиц.
4) Вычислить определители, составленные из координат векторов и выяснить, какая из систем векторов линейно независима. Разложить по ней вектор р = (5,5; 3; 1):
а) а1 = (2; 2; 0); а2 = (1; -1; 2); а3 = (1; 3; -2);
б) b 1 = (2; 1; 0); b 2 = (3; 0; -1); b 3 = (0; 2; 3).
5) Вычислить пределы:
а)  ; б)
; б)  .
.
6) Найти производную функции (y/x) и вычислить ее значение при x = 1:
а) y = x 3 e - x, б)  ; в) x 2 +3 y 2 =4.
; в) x 2 +3 y 2 =4.
7) Исследовать функцию у =0,5х4 – 4х2 и построить ее график.
8) Изобразить на плоскости xOy область определения функции двух переменных 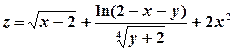 .
.
9) Найти 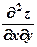 , если
, если  .
.
10) Найти стационарные точки и исследовать на экстремум функцию
z = 4 x – x 2 + 5 y – y 2 – xy .
8) Вычислить интегралы:
а) 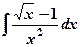 ; б)
; б) 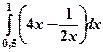 ; в)
; в)  .
.
9) Найти общее решение дифференциального уравнения
(1+у2) d х + xy d у = 0.
10) Найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами
у // – 4у=0.
Вариант 3.
1) Решить систему уравнений. Сделать проверку.
2 x + 3 y + z = 1 ,
3 x + y + 2 z = 9 ,
x – 2 y – 3 z = 4 .
2) Записать в виде системы линейных уравнений и решить эту систему методом Гаусса. Сделать проверку.
(х1 х2 х3) 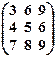 = (0 0 0).
= (0 0 0).
3) Построить бюджетное множество, отражающее покупательные возможности потребителя двух товаров по цене 120 и 80 руб., если на их приобретение можно израсходовать не более 5000 руб. и второго товара требуется не менее 40 единиц.
4) Выяснить, какая из систем векторов линейно независима, и разложить по ней вектор р = (6,75; 4; 1):
а) а1 = (3; 4; 0); а2 = (1; -1; 2); а3 = (1,5; 3; -6/7)
б) b 1 = (2; 1; 0); b 2 = (3; 0; -1); b 3 = (0; 4; 5).
5) Вычислить пределы:
а) 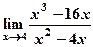 ; б)
; б) 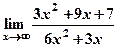 .
.
6) Найти производную функции (y/x) и вычислить ее значение при x = –1:
а) 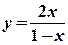 ; б) y = ex ( x +3); в) y ln (2+ x )+ y 2 =4.
; б) y = ex ( x +3); в) y ln (2+ x )+ y 2 =4.
7) Исследовать функцию у = х3/3 – х2/2 – 2х+3 и построить ее график.
8) Изобразить на плоскости xOy область определения функции двух переменных 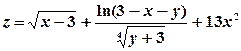 .
.
9) Найти  , если
, если 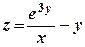 .
.
10) Найти стационарные точки и исследовать на экстремум функцию
z = 2 xy – 4 x – 2 y .
Вариант 4.
1) Решить систему уравнений. Сделать проверку.
3 x + 2 y + z = 1 ,
2 x + y + 3 z = 4 ,
x – 3 y – 2 z = 9 .
2) Записать в виде системы линейных уравнений и решить эту систему методом Гаусса. Сделать проверку.
(х1 х2 х3) 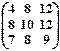 = (0 0 0).
= (0 0 0).
3) Построить бюджетное множество, отражающее покупательные возможности потребителя двух товаров по цене 200 и 160 руб., если на их приобретение можно израсходовать не более 4000 руб. а первого товара имеется не более 12 единиц.
4) Выяснить, какая из систем векторов линейно независима, и разложить по ней вектор р = (8,3; 5; 1):
а) а1 = (4; 10; 0); а2 = (1; -1; 2); а3 = (2; 3; 8/7);
б) b 1 = (2; 1; 0); b 2 = (3; 0; -1); b 3 = (0; 10; 11).
5) Вычислить пределы:
а) 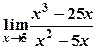 ; б)
; б) 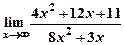
6) Найти производную функции (y/x) и вычислить ее значение при x = 1:
а) 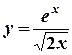 ; б) y = (1+ x ) lnx ; в) x 2 – xy – 2 y 2 = 0 .
; б) y = (1+ x ) lnx ; в) x 2 – xy – 2 y 2 = 0 .
7) Исследовать функцию у =х3 – 3х2 + 2 и построить ее график.
8) Изобразить на плоскости xOy область определения функции двух переменных 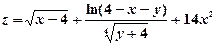 .
.
9) Найти  , если
, если  .
.
10) Найти стационарные точки и исследовать на экстремум функцию
z = 3 x + 6 y – x 2 – xy – y 2.
Вариант 5.
1) Решить систему уравнений. Сделать проверку.
3 x + y + 2 z = 4 ,
x + 2 y + 3 z = 1 ,
2 x – 3 y – z = 9 .
2) Записать в виде системы линейных уравнений и решить эту систему методом Гаусса. Сделать проверку.
(х1 х2 х3) 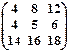 = (0 0 0).
= (0 0 0).
3) Построить бюджетное множество, отражающее покупательные возможности потребителя двух товаров по цене 40 и 90 руб., если на их приобретение можно израсходовать не более 2500 руб. и второго товара требуется не менее 10 единиц.
4) Выяснить, какая из систем векторов линейно независима, и разложить по ней вектор р = (10,6; 6; 1):
а) а1 = (5; 5; 0); а2 = (1; -1; 2); а3 = (2,5; 3; -0,5);
б) b 1 = (2; 1; 0); b 2 = (3; 0; -1); b 3 = (0; 5; 6) .
5) Вычислить пределы:
а)  ; б)
; б) 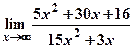 .
.
6) Найти производную функции (y/x) и вычислить ее значение при x = 0,5:
а) y = ln (1- x 2 ); б) 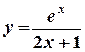 ; в) (1 – 2 x ) y 3 + y = 1 .
; в) (1 – 2 x ) y 3 + y = 1 .
7) Исследовать функцию у = 15х2 – 2х3 – 36х и построить ее график.
8) Изобразить на плоскости xOy область определения функции двух переменных 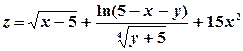 .
.
9) Найти 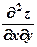 , если
, если  .
.
10) Найти стационарные точки и исследовать на экстремум функцию
z = x 2 + y 2 – 2 x – 2 y + 8 .
Вариант 6.
1) Решить систему уравнений. Сделать проверку.
2 x + y + 3 z = 9 ,
x + 3 y + 2 z = 1 ,
3 x – 2 y – z = 4 .
2) Записать в виде системы линейных уравнений и решить эту систему методом Гаусса. Сделать проверку.
(х1 х2 х3) 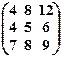 = (0 0 0).
= (0 0 0).
3) Построить бюджетное множество, отражающее покупательные возможности потребителя двух товаров по цене 135 и 165 руб., если на их приобретение можно израсходовать не более 3000 руб. а первого товара имеется не более 10 единиц.
4) Выяснить, какая из систем векторов линейно независима, и разложить по ней вектор р = (13; 7; 1):
а) а1 = (6; 3; 0); а2 = (1; -1; 2); а3 = (3; 3; -2);
б) b 1 = (2; 1; 0); b 2 = (3; 0; -1); b 3 = (0; 3; 4).
5) Вычислить пределы: а)  ; б)
; б) 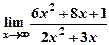 .
.
6) Найти производную функции (y/x) и вычислить ее значение при x = 0:
а) 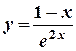 ; б)
; б) 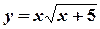 ; в) y 2 ln (1+ x )+2 y +2=0 .
; в) y 2 ln (1+ x )+2 y +2=0 .
7) Исследовать функцию у = 0,25х2(х+3) – 5 и построить ее график.
8) Изобразить на плоскости xOy область определения функции двух переменных 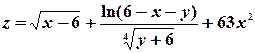 .
.
9) Найти 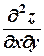 , если
, если 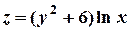 .
.
10) Найти стационарные точки и исследовать на экстремум функцию z = x 2 + xy + y 2 – 3 x – 6 y .
Вариант 7.
1) Решить систему уравнений. Сделать проверку.
4 x + y + 5 z = 25 ,
x + 5 y + 4 z = 1 ,
5 x – 4 y – z = 16 .
2) Записать в виде системы линейных уравнений и решить эту систему методом Гаусса. Сделать проверку.
(х1 х2 х3) 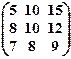 = (0 0 0).
= (0 0 0).
3) Построить бюджетное множество, отражающее покупательные возможности потребителя двух товаров по цене 65 и 95 руб., если на их приобретение можно израсходовать не более 4300 руб. и второго товара требуется не менее 15 единиц.
4) Выяснить, какая из систем векторов линейно независима, и разложить по ней вектор р = (15,5; 8; 1):
а) а1 = (7; 2; 0); а2 = (1; -1; 2); а3 = (3,5; 3; -28/9);
б) b 1 = (2; 1; 0); b 2 = (3; 0; -1); b 3 = (0; 2; 3)..
5) Вычислить пределы:
а)  ; б)
; б) 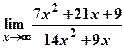 .
.
6) Найти производную функции (y/x) и вычислить ее значение при x = 1:
а) y = (1–2х)5 ; б) 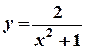 ; в) y +(1+ y 2 ) lnx =1 .
; в) y +(1+ y 2 ) lnx =1 .
7) Исследовать функцию у =х3 – 3х и построить ее график.
8) Изобразить на плоскости xOy область определения функции двух переменных 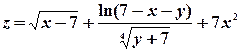 .
.
9) Найти 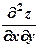 , если
, если 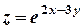 .
.
10) Найти стационарные точки и исследовать на экстремум функцию
z = x – x 2 + y 2 + 2 y .
Вариант 8.
1) Решить систему уравнений. Сделать проверку.
4 x + 5 y + z = 1 ,
5 x + y + 4 z = 25 ,
x – 4 y – 5 z = 16 .
2) Записать в виде системы линейных уравнений и решить эту систему методом Гаусса. Сделать проверку.
(х1 х2 х3)  = (0 0 0).
= (0 0 0).
3) Построить бюджетное множество, отражающее покупательные возможности потребителя двух товаров по цене 40 и 70 руб., если на их приобретение можно израсходовать не более 4500 руб. а первого товара имеется не более 30 единиц.
4) Выяснить, какая из систем векторов линейно независима, и разложить по ней вектор р = (16,75; 9; 1):
а) а1 = (8; 4; 0); а2 = (1; -1; 2); а3 = (4; 3; -4/3);
б) b 1 = (2; 1; 0); b 2 = (3; 0; -1); b 3 = (0; 4; 5).
.
5) Вычислить пределы:
а) 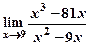 ; б)
; б) 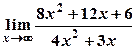 .
.
6) Найти производную функции (y/x) и вычислить ее значение при x = 0:
а) y = (3х2-6 x )ех ; б)  ; в) 2 x 2 + xy 2 + y = 0 .
; в) 2 x 2 + xy 2 + y = 0 .
7) Исследовать функцию у = 12х – х3 и построить ее график.
8) Изобразить на плоскости xOy область определения функции двух переменных  .
.
9) Найти 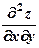 , если
, если 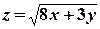 .
.
10) Найти стационарные точки и исследовать на экстремум функцию
z = x 2 + xy + y 2 – 6 x – 9 y .
Вариант 9.
1) Решить систему уравнений. Сделать проверку.
4 x + 3 y + 2 z = 4 ,
3 x + 2 y + 4 z = 9 ,
2 x – 4 y – 3 z = 16 .
2) Записать в виде системы линейных уравнений и решить эту систему методом Гаусса. Сделать проверку.
(х1 х2 х3) 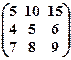 = (0 0 0).
= (0 0 0).
3) Построить бюджетное множество, отражающее покупательные возможности потребителя двух товаров по цене 150 и 90 руб., если на их приобретение можно израсходовать не более 5100 руб. и второго товара требуется не менее 15 единиц.
4) Выяснить, какая из систем векторов линейно независима, и разложить по ней вектор р = (18,3; 10; 1):
а) а1 = (9; 10; 0); а2 = (1; -1; 2); а3 = (4,5; 3; 36/19);
б) b 1 = (2; 1; 0); b 2 = (3; 0; -1); b 3 = (0; 10; 11)..
5) Вычислить пределы:
а) 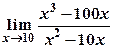 ; б)
; б) 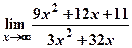 .
.
6) Найти производную функции (y/x) и вычислить ее значение при x = 1:
а) y = ln (7х – 3) ; б) 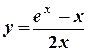 ; в)
; в) 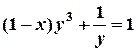 .
.
7) Исследовать функцию у = х(х2 – 3)+4 и построить ее график.
8) Изобразить на плоскости xOy область определения функции двух переменных 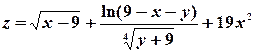 .
.
9) Найти  , если
, если 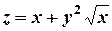 .
.
10) Найти стационарные точки и исследовать на экстремум функцию
z = 0,5 x 2 + 2 xy + 0,5 y 2 – 4 x – 5 y .
Вариант 10.
1) Решить систему уравнений. Сделать проверку.
2 x + 4 y + 5 z = 25 ,
4 x + 5 y + 2 z = 16 ,
5 x – 2 y – 4 z = 4 .
2) Записать в виде системы линейных уравнений и решить эту систему методом Гаусса. Сделать проверку.
(х1 х2 х3) 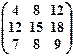 = (0 0 0).
= (0 0 0).
3) Построить бюджетное множество, отражающее покупательные возможности потребителя двух товаров по цене 105 и 70 руб., если на их приобретение можно израсходовать не более 4200 руб. а первого товара имеется не более 20 единиц.
4) Выяснить, какая из систем векторов линейно независима, и разложить по ней вектор р = (20,6; 11; 1):
а) а1 = (10; 5; 0); а2 = (1; -1; 2); а3 = (5; 3; -2/3);
б) b 1 = (2; 1; 0); b 2 = (3; 0; -1); b 3 = (0; 5; 6).
5) Вычислить пределы:
а) 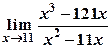 ; б)
; б) 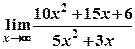 .
.
6) Найти производную функции (y/x) и вычислить ее значение при x = – 1:
а) y = ln (х2 – 4х) ; б)  ; в)
; в)  .
.
7) Исследовать функцию у =3х – х3 – 2 и построить ее график.
8) Изобразить на плоскости xOy область определения функции двух переменных  .
.
9) Найти  , если
, если 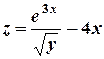 .
.
10) Найти стационарные точки и исследовать на экстремум функцию
z = 2 xy – 3 x 2 – 2 y 2 + 10 .
Вариант 1.
Вычислить интегралы:
1) Вычислить неопределенные интегралы: а) 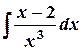 ; б)
; б) 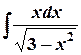
2) Вычислить определенный интеграл 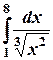 ;
;
3). Найти общее решение дифференциального уравнения
y / (1+ ex ) y = ex .
4) Найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами
у // - 2у /+у=0.
5) Написать первые три члена ряда и проверить необходимый признак сходимости для заданного числового ряда 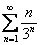
6) Из полного набора домино наугад взяли одну кость. Найти вероятность того, что сумма очков на ней равна 4.
7) Судоходная компания организует средиземноморские круизы в течение летнего времени и проводит несколько круизов в сезон. Чтобы получить прибыль, важно, чтобы все каюты зафрахтованного под круизы корабля были полностью заняты туристами. Эксперт по туризму, нанятый компанией, предсказывает, что корабль будет полон в течение сезона с вероятностью 0,92, если доллар не подорожает по отношению к рублю, и с вероятностью 0,75, если доллар подорожает. По оценкам экономистов, вероятность того, что в течение сезона доллар подорожает по отношению к рублю, равна 0,23. Чему равна вероятность того, что билеты на все круизы будут проданы.
8) Задан закон распределения дискретной случайной величины.
| X | – 4 | – 1 | 2 | 5 | 8 |
| p | 0,2 | 0,3 | 0,25 | 0,15 | 0,1 |
Найти математическое ожидание, дисперсию и с.к.о.
9) Вероятность появления события А при одном испытании равна 0,1. Найти вероятность того, что при трех независимых испытаниях оно появится хотя бы один раз.
10) Зная математическое ожидание т = 15 и среднее квадратичное отклонение s = 2 нормально распределенной случайной величины Х, найти вероятность того, что а) Х примет значение из интервала (9; 19),
б) выполнится неравенство |Х – т| < 3.
Вариант 2.
1) Вычислить неопределенные интегралы:
а)  ; б); в)
; б); в) 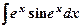 .
.
2) Вычислить определенный интеграл 
а)
3) Найти общее решение дифференциального уравнения
(1+у2) d х + xy d у = 0.
4) Найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами
у // – 4у=0.
5) Написать первые три члена ряда и проверить необходимый признак сходимости для заданного числового ряда 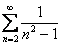
6) При наборе телефонного номера абонент забыл три последние цифры и набрал их наугад, помня только, что эти цифры разные. Найти вероятность того, что номер набран правильно.
7) Два автомата производят одинаковые детали, которые поступают на общий конвейер. Производительность первого автомата вдвое больше производительности второго. Первый автомат производит в среднем 60% деталей отличного качества, а второй – 84% деталей отличного качества. Наудачу взятая с конвейера деталь оказалась отличного качества. Найти вероятность того, что эта деталь изготовлена первым автоматом.
8) Задан закон распределения дискретной случайной величины.
| X | 19 | 21 | 23 | 25 | 27 |
| p | 0,2 | 0,3 | 0,25 | 0,15 | 0,1 |
Найти математическое ожидание, дисперсию и с.к.о.
9) Найти вероятность того, что событие А произойдет не менее двух раз в 4 независимых испытаниях, если вероятность наступления события А в одном испытании равна 0,6.
10) Зная математическое ожидание т = 14 и среднее квадратичное отклонение s = 4 нормально распределенной случайной величины Х, найти вероятность того, что а) Х примет значение из интервала (10; 20), б) выполнится неравенство |Х – т| < 4.
Вариант 3.
1) Вычислить неопределенные интегралы: а) 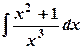 ; б)
; б) 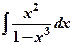 .
.
2) Вычислить определенный интеграл 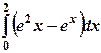
3) Найти общее решение дифференциального уравнения
(1+ x ) y d х + x (1 – y ) d у = 0.
4) Найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами у //+3у /+2у =0.
5) Написать первые три члена ряда и проверить необходимый признак сходимости для заданного числового ряда 
6) В общежитии живут 30 первокурсников, 35 второкурсников, 20 третьекурсников и 15 студентов четвертого курса. Какова вероятность того, что два случайно встреченных студента окажутся с первого курса?
7) Экономист-аналитик условно подразделяет экономическую ситуацию в стране на «хорошую», «посредственную» и «плохую» и оценивает их вероятности для данного момента времени в 0,15; 0,70 и 0,15 соответственно. Некоторый индекс экономического состояния возрастает с вероятностью 0,60, когда ситуация «хорошая»; с вероятностью 0,30, когда ситуация «посредственная», и с вероятностью 0,10, когда ситуация «плохая». Найти вероятность возрастания этого индекса.
8) Задан закон распределения дискретной случайной величины.
| X | 9 | 12 | 15 | 18 | 21 |
| p | 0,2 | 0,3 | 0,25 | 0,15 | 0,1 |
Найти математическое ожидание, дисперсию и с.к.о.
9) В ящике имеется по одинаковому числу деталей, изготовленных заводами №1 и №2. Найти вероятность того, что среди пяти наудачу отобранных деталей менее двух изготовлены на заводе №1.
10). Зная математическое ожидание т = 13 и среднее квадратичное отклонение s = 4 нормально распределенной случайной величины Х, найти вероятность того, что а) Х примет значение из интервала (11; 21), б) выполнится неравенство |Х – т| < 8.
Вариант 4.
1) Вычислить неопределенные интегралы:
а) 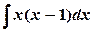 ; б)
; б)  .
.
2) Вычислить определенный интеграл: 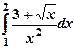 .
.
3) Найти общее решение дифференциального уравнения
 .
.
4) Найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами
у // + 16у=0.
5) Написать первые три члена ряда и проверить необходимый признак сходимости для заданного числового ряда 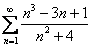
6) Собрание, на котором присутствует 15 человек, в том числе 5 женщин, выбирает делегацию из 3-х человек. Считая, что каждый из присутствующих с одинаковой вероятностью может быть избран, найти
Вероятность того, что в состав делегации войдут две женщины и один мужчина.
7) Из числа авиалиний некоторого аэропорта 60% – местные, 30% – по СНГ и 10% – международные. Среди пассажиров местных авиалиний 50% путешествуют по делам, связанным с бизнесом, на линиях СНГ таких пассажиров 60%, на международных – 90%. Из прибывших в аэропорт пассажиров случайно выбирается один. Чему равна вероятность того, что он бизнесмен?
8) Задан закон распределения дискретной случайной величины.
| X | 0 | 2 | 4 | 6 | 8 |
| p | 0,2 | 0,3 | 0,25 | 0,15 | 0,1 |
Найти математическое ожидание, дисперсию и с.к.о.
9) Вероятность выигрыша по одному билету лотереи равна 0,1. Куплено 4 билета. Найти вероятность того, что выиграет не более одного билета.
10) Зная математическое ожидание т = 12 и среднее квадратичное отклонение s = 5 нормально распределенной случайной величины Х, найти вероятность того, что а) Х примет значение из интервала (12; 22), б) выполнится неравенство |Х – т| < 10.
Вариант 5.
Вариант 6.
1) Вычислить неопределенные интегралы а)  ; б)
; б) 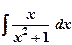 .
.
2) Вычислить определенный интеграл: 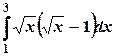 .
.
3) Найти общее решение дифференциального уравнения
y / = ex +у .
4) Найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами
у // - 2у /+2у=0.
5) Написать первые три члена ряда и проверить необходимый признак сходимости для заданного числового ряда 
6) Ребенок играет с буквами разрезной азбуки А, Г, И, К, Н. Найти вероятность того, что при случайном расположении букв в ряд он получит слово «КНИГА».
7) Международная компания обсуждает возможности инвестиций в некоторое государство с неустойчивой политической ситуацией. Менеджеры оценивают вероятность успеха в 0,55, если преобладающая политическая ситуация будет благоприятной; в 0,30, если политическая ситуация будет нейтральной; в 0,10, если политическая ситуация в течение года будет неблагоприятной. Предполагается, что вероятности благоприятной, нейтральной и неблагоприятной политических ситуаций соответственно равны: 0,60, 0,20 и 0,20. Чему равна вероятность успеха инвестиций?
8) Задан закон распределения дискретной случайной величины.
| X | 12 | 14 | 16 | 18 | 20 |
| p | 0,2 | 0,3 | 0,25 | 0,15 | 0,1 |
Найти математическое ожидание, дисперсию и с.к.о.
9) Вероятность того, что в течение гарантийного срока телевизор потребует ремонта, равна 0,2. Найти вероятность того, что в течение гарантийного срока из 6 телевизоров не более одного потребуют ремонта.
10) Зная математическое ожидание т = 10 и среднее квадратичное отклонение s = 8 нормально распределенной случайной величины Х, найти вероятность того, что а) Х примет значение из интервала (14; 18), б) выполнится неравенство |Х – т| < 2.
Вариант 7.
1) Вычислить неопределенные интегралы:
а) 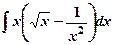 ; б)
; б) 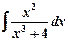 .
.
2) Вычислить определенный интеграл: 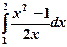
3) Найти общее решение дифференциального уравнения
ey (1+x2) dy – 2x (1+ ey) dx = 0.
4)Найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами
у // + 3у / = 0.
5) Написать первые три члена ряда и проверить необходимый признак сходимости для заданного числового ряда 
6) Из полной колоды карт (52 листа) вынимают сразу четыре карты. Найти вероятность того, что все эти карты будут разных мастей.
7) Два кирпичных завода поставляют одну и ту же марку кирпича на стройку. Первый завод поставляет каждый день 3000 кирпичей, второй – 5000 кирпичей. Известно, что 80% продукции первого завода и 96% продукции второго завода является стандартной. Найти вероятность того, что наугад выбранный из ежедневной поставки кирпич окажется нестандартным?
8) Задан закон распределения дискретной случайной величины.
| X | 1 | 4 | 7 | 10 | 13 |
| p | 0,2 | 0,3 | 0,25 | 0,15 | 0,1 |
Найти математическое ожидание, дисперсию и с.к.о.
9) Вероятность быть принятым на работу в некоторую фирму равна 0,8. Найти вероятность того, что из трех человек, пришедших на собеседование, только двое будут приняты на работу.
10) Зная математическое ожидание т = 9 и среднее квадратичное отклонение s = 3 нормально распределенной случайной величины Х, найти вероятность того, что а) Х примет значение из интервала (9; 18), б) выполнится неравенство |Х – т| < 6.
Вариант 8.
1) Вычислить неопределенные интегралы:
а)  ; б)
; б) 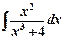 .
.
2) Вычислить определенный интеграл:  ;
;
3) Найти общее решение дифференциального уравнения
ey (1+x2) dy – 2x (1+ ey) dx = 0.
4)Найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами
у // + 3у / = 0.
5) Написать первые три члена ряда и проверить необходимый признак сходимости для заданного числового ряда 
6) Два стрелка сделали по одному выстрелу по мишени. Вероятность попадания для одного из стрелков равна 0,6. Для другого – 0,7. Найти вероятность того, что хотя бы один из стрелков попадет в мишень.
7) При слиянии акционерного капитала двух фирм аналитики фирмы, получающей контрольный пакет акций, полагают, что сделка принесет успех с вероятностью, равной 0,65, если председатель совета директоров поглощаемой фирмы выйдет в отставку; если он откажется, то вероятность успеха будет равна 0,30. Предполагается, что вероятность ухода в отставку председателя составляет 0,70. Чему равна вероятность успеха сделки?
8) Задан закон распределения дискретной случайной величины.
| X | 4 | 6 | 8 | 10 | 12 |
| p | 0,2 | 0,3 | 0,25 | 0,15 | 0,1 |
Найти математическое ожидание, дисперсию и с.к.о.
9) Вероятность попадания в цель при одном выстреле равна 0,2. Сделано 10 выстрелов. Найти вероятность хотя бы одного попадания в цель.
10) Зная математическое ожидание т = 8 и среднее квадратичное отклонение s = 4 нормально распределенной случайной величины Х, найти вероятность того, что а) Х примет значение из интервала (8; 12), б) выполнится неравенство |Х – т| < 8.
Вариант 9.
1) Вычислить неопределенные интегралы: а) 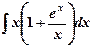 ; б)
; б)  .
.
2)Вычислить определенный интеграл: 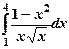 .
.
3) Найти общее решение дифференциального уравнения
(xy2+x) dx + (y– x2y) dy = 0.
4)Найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами у // + у / – 2 y = 0.
5) Написать первые три члена ряда и проверить необходимый признак сходимости для заданного числового ряда 
6) Вероятность, что при нажиме стартера мотор машины заработает, равна примерно 5/6. Найти вероятность того, что мотор включится только при повторном нажиме стартера.
7) Проведя предварительные исследования, нефтеразведчики полагают, что вероятность наличия нефти на проверяемом участке равна 0,4. На завершающем этапе разведки проводится сейсмический тест, который имеет определенную степень надежности: если на проверяемом участке есть нефть, то тест укажет на ее наличие в 85% случаев; если нефти нет, то в 10% случаев тест может ошибочно указать ее присутствие. Сейсмический тест указал на присутствие нефти. Чему равна вероятность того, что запасы нефти на данном участке существуют реально?
8) Задан закон распределения дискретной случайной величины.
| X | – 1 | 2 | 5 | 8 | 11 |
| p | 0,2 | 0,3 | 0,25 | 0,15 | 0,1 |
Найти математическое ожидание, дисперсию и с.к.о.
9) В ящике лежат несколько тысяч одинаковых предохранителей. Половина из них изготовлена первым заводом, остальные – вторым заводом. Наудачу вынули пять предохранителей. Найти вероятность того, что среди них более двух изготовлено первым заводом.
10) Зная математическое ожидание т = 7 и среднее квадратичное отклонение s = 2 нормально распределенной случайной величины Х, найти вероятность того, что а) Х примет значение из интервала (6; 10), б) выполнится неравенство |Х – т| < 4.
Вариант 10.
1) Вычислить неопределенные интегралы а) 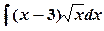 ; б)
; б) 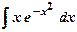 .
.
2) Вычислить определенный интеграл 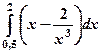 ;
;
3) Найти общее решение дифференциального уравнения (2 y +1) x dx + (1+ x 2 ) dy = 0.
4)Найти общее решение линейного однородного дифференциального
уравнения с постоянными коэффициентами у // - 2у / = 0.
5) Написать первые три члена ряда и проверить необходимый признак сходимости для заданного числового ряда 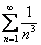
6) Охотник выстрелил три раза по удаляющейся цели. Вероятность попадания в нее в начале стрельбы равна 0,8, а после каждого выстрела уменьшается на 0,1. Найти вероятность того, что он промахнется все три раза.
7) Исследованиями психологов установлено, что мужчины и женщины по-разному реагируют на некоторые жизненные обстоятельства. Результаты исследований показали, что позитивно реагируют на изучаемый круг ситуаций 70% женщин и только 60% мужчин. 15 женщин и 5 мужчин заполнили анкету, в которой отразили свое отношение к предлагаемым ситуациям. Случайно извлеченная анкета содержит негативную реакцию. Чему равна вероятность того, что ее заполнял мужчина?
8) Задан закон распределения дискретной случайной величины.
| X | – 1 | 1 | 3 | 5 | 7 |
| p | 0,2 | 0,3 | 0,25 | 0,15 | 0,1 |
Найти математическое ожидание, дисперсию и с.к.о.
9) Вероятность того, что проверяемое изделие нестандартно, равна 0,1. Найти вероятность того, что из трех проверенных изделий только одно нестандартное.
10) Зная математическое ожидание т = 6 и среднее квадратичное отклонение s = 2 нормально распределенной случайной величины Х, найти вероятность того, что а) Х примет значение из интервала (4; 12), б) выполнится неравенство |Х – т| < 4.
МАТЕМАТИКА
Учебно-методическое пособие
Самара 2017
| УДК 51 | |
| ББК 22.1 | |
|
| |
|
| |
| Математика. Учебно-методическое пособие /Составитель Коваленко Т.Д. – Самара: Университет «МИР», 2017. – 43 с. | |
|
| |
|
| |
| Методическое пособие по дисциплине «Математика» включает содержание тематических разделов дисциплины, материалы для текущего контроля, пример оценочных материалов для промежуточной аттестации. | |
| Методическое пособие предназначено для студентов, обучающихся по направлению «Менеджмент», профили «Маркетинг» и «Менеджмент организации». | |
| Составитель: | Коваленко Татьяна Дмитриевна |
| к.т.н., доцент | |
| Рецензент: | Горбунова Оксана Александровна |
| к.э.н., доцент | |
| Печатается по решению Учебно-методического совета АНО ВО Университета «МИР» | |
| © АНО ВО Университет «МИР», 2017 | |
| © Составление: Коваленко Т.Д., 2017 | |
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ .. 4
СОДЕРЖАНИЕ ТЕМАТИЧЕСКИХ РАЗДЕЛОВ ДИСЦИПЛИНЫ ... 4
ПЕРЕЧЕНЬ УЧЕБНО-МЕТОДИЧЕСКОГО И ИНФОРМАЦИОННОГО ОБЕСПЕЧЕНИЯ ДИСЦИПЛИНЫ ... 6
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ПРЕПОДАВАТЕЛЯ .. 6
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ СТУДЕНТОВ .. 9
ФОНД ОЦЕНОЧНЫХ СРЕДСТВ (для проведения экзамена) 10
Дата: 2019-05-28, просмотров: 482.