| Критерии | Максимальное количество баллов |
| При выполнении заданий приводятся верные основные теоретические положения и формулы | 3 баллов |
| Правильно выполнены расчеты | 3 баллов |
| Правильно построены графики | 3 баллов |
| Оформление соответствует образцу | 1 баллов |
| Итого Верно выполненное задание | 10 баллов |
Расчетно-графическая работа оценивается по 10 балльной шкале, баллы переводятся в оценки успеваемости следующим образом:
• 0-4 баллов – «2»;
• 5-6 баллов – «3».
• 7-8 баллов – «4».
• 9-10 баллов – «5».
Варианты заданий контрольной работы для заочной формы обучения
Контрольная работа №1 первый семестр
Вариант 1.
1) Решить систему уравнений по формулам определителей Крамера. Сделать проверку.
x + 2 y + 3 z = 9 ,
2 x + 3 y + z = 4 ,
3 x – y – 2 z = 1 .
2) Записать матричное уравнение в виде системы линейных уравнений и решить методом Гаусса. Сделать проверку.
(х1 х2 х3) 
= (0 0 0).
3) Пользуясь геометрическим смыслом системы линейных неравенств, построить бюджетное множество, отражающее покупательные возможности потребителя двух товаров по цене 75 и 50 руб., если на их приобретение можно израсходовать не более 3000 руб. и второго товара требуется не менее 15 единиц.
4) Вычислить определитель, составленный из координат векторов и выяснить, какая из систем векторов линейно независима. Разложить по ней вектор р = (3; 2; 1):
а) а1 = (1; 3; 0); а2 = (1; -1; 2); а3 = (1/2; 3; -3/4);
б) b 1 = (2; 1; 0); b 2 = (3; 0; -1); b 3 = (0; 3; 4).
5) Вычислить пределы:
а)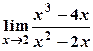 
; б)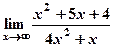 
.
6) Найти производную функции (y/x) и вычислить ее значение при x = 1:
а) y = x2 lnx ; б)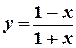 
; в) x 3 + xy + y 2 =3 .
7) Исследовать функцию у =2х3+3х2–1 и построить ее график.
8) Изобразить на плоскости xOy область определения функции двух переменных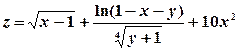 
.
9) Найти 
, если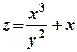 
.
10) Найти стационарные точки и исследовать на экстремум функцию
z = x 2 – xy + y 2 + 9 x – 6 y + 20 .
Вариант 2.
1) Решить систему уравнений. Сделать проверку.
x + 3 y + 2 z = 4 ,
3 x + 2 y + z = 9 ,
2 x – y – 3 z = 1 .
2) Записать в виде системы линейных уравнений и решить эту систему методом Гаусса. Сделать проверку.
(х1 х2 х3)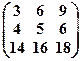 
= (0 0 0).
3) Построить бюджетное множество, отражающее покупательные возможности потребителя двух товаров по цене 175 и 70 руб., если на их приобретение можно израсходовать не более 3500 руб. а первого товара имеется не более 15 единиц.
4) Вычислить определители, составленные из координат векторов и выяснить, какая из систем векторов линейно независима. Разложить по ней вектор р = (5,5; 3; 1):
а) а1 = (2; 2; 0); а2 = (1; -1; 2); а3 = (1; 3; -2);
б) b 1 = (2; 1; 0); b 2 = (3; 0; -1); b 3 = (0; 2; 3).
5) Вычислить пределы:
а) 
; б) 
.
6) Найти производную функции (y/x) и вычислить ее значение при x = 1:
а) y = x 3 e - x, б) 
; в) x 2 +3 y 2 =4.
7) Исследовать функцию у =0,5х4 – 4х2 и построить ее график.
8) Изобразить на плоскости xOy область определения функции двух переменных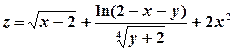 
.
9) Найти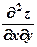 
, если 
.
10) Найти стационарные точки и исследовать на экстремум функцию
z = 4 x – x 2 + 5 y – y 2 – xy .
8) Вычислить интегралы:
а)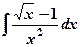 
; б) 
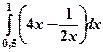; в) 
.
9) Найти общее решение дифференциального уравнения
(1+у2) d х + xy d у = 0.
10) Найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами
у // – 4у=0.
Вариант 3.
1) Решить систему уравнений. Сделать проверку.
2 x + 3 y + z = 1 ,
3 x + y + 2 z = 9 ,
x – 2 y – 3 z = 4 .
2) Записать в виде системы линейных уравнений и решить эту систему методом Гаусса. Сделать проверку.
(х1 х2 х3)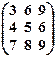 
= (0 0 0).
3) Построить бюджетное множество, отражающее покупательные возможности потребителя двух товаров по цене 120 и 80 руб., если на их приобретение можно израсходовать не более 5000 руб. и второго товара требуется не менее 40 единиц.
4) Выяснить, какая из систем векторов линейно независима, и разложить по ней вектор р = (6,75; 4; 1):
а) а1 = (3; 4; 0); а2 = (1; -1; 2); а3 = (1,5; 3; -6/7)
б) b 1 = (2; 1; 0); b 2 = (3; 0; -1); b 3 = (0; 4; 5).
5) Вычислить пределы:
а)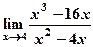 
; б)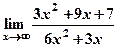 
.
6) Найти производную функции (y/x) и вычислить ее значение при x = –1:
а)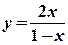 
; б) y = ex ( x +3); в) y ln (2+ x )+ y 2 =4.
7) Исследовать функцию у = х3/3 – х2/2 – 2х+3 и построить ее график.
8) Изобразить на плоскости xOy область определения функции двух переменных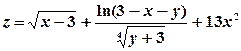 
.
9) Найти 
, если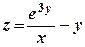 
.
10) Найти стационарные точки и исследовать на экстремум функцию
z = 2 xy – 4 x – 2 y .
Вариант 4.
1) Решить систему уравнений. Сделать проверку.
3 x + 2 y + z = 1 ,
2 x + y + 3 z = 4 ,
x – 3 y – 2 z = 9 .
2) Записать в виде системы линейных уравнений и решить эту систему методом Гаусса. Сделать проверку.
(х1 х2 х3)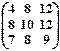 
= (0 0 0).
3) Построить бюджетное множество, отражающее покупательные возможности потребителя двух товаров по цене 200 и 160 руб., если на их приобретение можно израсходовать не более 4000 руб. а первого товара имеется не более 12 единиц.
4) Выяснить, какая из систем векторов линейно независима, и разложить по ней вектор р = (8,3; 5; 1):
а) а1 = (4; 10; 0); а2 = (1; -1; 2); а3 = (2; 3; 8/7);
б) b 1 = (2; 1; 0); b 2 = (3; 0; -1); b 3 = (0; 10; 11).
5) Вычислить пределы:
а)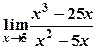 
; б)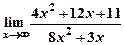 
6) Найти производную функции (y/x) и вычислить ее значение при x = 1:
а)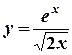 
; б) y = (1+ x ) lnx ; в) x 2 – xy – 2 y 2 = 0 .
7) Исследовать функцию у =х3 – 3х2 + 2 и построить ее график.
8) Изобразить на плоскости xOy область определения функции двух переменных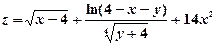 
.
9) Найти 
, если 
.
10) Найти стационарные точки и исследовать на экстремум функцию
z = 3 x + 6 y – x 2 – xy – y 2.
Вариант 5.
1) Решить систему уравнений. Сделать проверку.
3 x + y + 2 z = 4 ,
x + 2 y + 3 z = 1 ,
2 x – 3 y – z = 9 .
2) Записать в виде системы линейных уравнений и решить эту систему методом Гаусса. Сделать проверку.
(х1 х2 х3) 
= (0 0 0).
3) Построить бюджетное множество, отражающее покупательные возможности потребителя двух товаров по цене 40 и 90 руб., если на их приобретение можно израсходовать не более 2500 руб. и второго товара требуется не менее 10 единиц.
4) Выяснить, какая из систем векторов линейно независима, и разложить по ней вектор р = (10,6; 6; 1):
а) а1 = (5; 5; 0); а2 = (1; -1; 2); а3 = (2,5; 3; -0,5);
б) b 1 = (2; 1; 0); b 2 = (3; 0; -1); b 3 = (0; 5; 6) .
5) Вычислить пределы:
а) 
; б)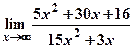 
.
6) Найти производную функции (y/x) и вычислить ее значение при x = 0,5:
а) y = ln (1- x 2 ); б)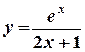 
; в) (1 – 2 x ) y 3 + y = 1 .
7) Исследовать функцию у = 15х2 – 2х3 – 36х и построить ее график.
8) Изобразить на плоскости xOy область определения функции двух переменных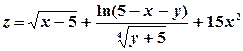 
.
9) Найти 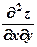, если 
.
10) Найти стационарные точки и исследовать на экстремум функцию
z = x 2 + y 2 – 2 x – 2 y + 8 .
Вариант 6.
1) Решить систему уравнений. Сделать проверку.
2 x + y + 3 z = 9 ,
x + 3 y + 2 z = 1 ,
3 x – 2 y – z = 4 .
2) Записать в виде системы линейных уравнений и решить эту систему методом Гаусса. Сделать проверку.
(х1 х2 х3)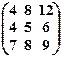 
= (0 0 0).
3) Построить бюджетное множество, отражающее покупательные возможности потребителя двух товаров по цене 135 и 165 руб., если на их приобретение можно израсходовать не более 3000 руб. а первого товара имеется не более 10 единиц.
4) Выяснить, какая из систем векторов линейно независима, и разложить по ней вектор р = (13; 7; 1):
а) а1 = (6; 3; 0); а2 = (1; -1; 2); а3 = (3; 3; -2);
б) b 1 = (2; 1; 0); b 2 = (3; 0; -1); b 3 = (0; 3; 4).
5) Вычислить пределы: а) 
; б)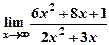 
.
6) Найти производную функции (y/x) и вычислить ее значение при x = 0:
а)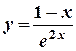 
; б)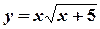 
; в) y 2 ln (1+ x )+2 y +2=0 .
7) Исследовать функцию у = 0,25х2(х+3) – 5 и построить ее график.
8) Изобразить на плоскости xOy область определения функции двух переменных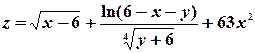 
.
9) Найти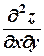 
, если 
.
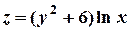10) Найти стационарные точки и исследовать на экстремум функцию z = x 2 + xy + y 2 – 3 x – 6 y .
Вариант 7.
1) Решить систему уравнений. Сделать проверку.
4 x + y + 5 z = 25 ,
x + 5 y + 4 z = 1 ,
5 x – 4 y – z = 16 .
2) Записать в виде системы линейных уравнений и решить эту систему методом Гаусса. Сделать проверку.
(х1 х2 х3)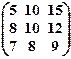 
= (0 0 0).
3) Построить бюджетное множество, отражающее покупательные возможности потребителя двух товаров по цене 65 и 95 руб., если на их приобретение можно израсходовать не более 4300 руб. и второго товара требуется не менее 15 единиц.
4) Выяснить, какая из систем векторов линейно независима, и разложить по ней вектор р = (15,5; 8; 1):
а) а1 = (7; 2; 0); а2 = (1; -1; 2); а3 = (3,5; 3; -28/9);
б) b 1 = (2; 1; 0); b 2 = (3; 0; -1); b 3 = (0; 2; 3)..
5) Вычислить пределы:
а) 
; б)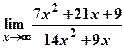 
.
6) Найти производную функции (y/x) и вычислить ее значение при x = 1:
а) y = (1–2х)5 ; б)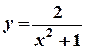 
; в) y +(1+ y 2 ) lnx =1 .
7) Исследовать функцию у =х3 – 3х и построить ее график.
8) Изобразить на плоскости xOy область определения функции двух переменных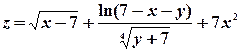 
.
9) Найти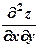 
, если 
.
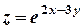10) Найти стационарные точки и исследовать на экстремум функцию
z = x – x 2 + y 2 + 2 y .
Вариант 8.
1) Решить систему уравнений. Сделать проверку.
4 x + 5 y + z = 1 ,
5 x + y + 4 z = 25 ,
x – 4 y – 5 z = 16 .
2) Записать в виде системы линейных уравнений и решить эту систему методом Гаусса. Сделать проверку.
(х1 х2 х3) 
= (0 0 0).
3) Построить бюджетное множество, отражающее покупательные возможности потребителя двух товаров по цене 40 и 70 руб., если на их приобретение можно израсходовать не более 4500 руб. а первого товара имеется не более 30 единиц.
4) Выяснить, какая из систем векторов линейно независима, и разложить по ней вектор р = (16,75; 9; 1):
а) а1 = (8; 4; 0); а2 = (1; -1; 2); а3 = (4; 3; -4/3);
б) b 1 = (2; 1; 0); b 2 = (3; 0; -1); b 3 = (0; 4; 5).
.
5) Вычислить пределы:
а)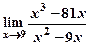 
; б)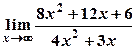 
.
6) Найти производную функции (y/x) и вычислить ее значение при x = 0:
а) y = (3х2-6 x )ех ; б) 
; в) 2 x 2 + xy 2 + y = 0 .
7) Исследовать функцию у = 12х – х3 и построить ее график.
8) Изобразить на плоскости xOy область определения функции двух переменных 
.
9) Найти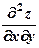 
, если 
.
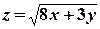10) Найти стационарные точки и исследовать на экстремум функцию
z = x 2 + xy + y 2 – 6 x – 9 y .
Вариант 9.
1) Решить систему уравнений. Сделать проверку.
4 x + 3 y + 2 z = 4 ,
3 x + 2 y + 4 z = 9 ,
2 x – 4 y – 3 z = 16 .
2) Записать в виде системы линейных уравнений и решить эту систему методом Гаусса. Сделать проверку.
(х1 х2 х3)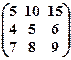 
= (0 0 0).
3) Построить бюджетное множество, отражающее покупательные возможности потребителя двух товаров по цене 150 и 90 руб., если на их приобретение можно израсходовать не более 5100 руб. и второго товара требуется не менее 15 единиц.
4) Выяснить, какая из систем векторов линейно независима, и разложить по ней вектор р = (18,3; 10; 1):
а) а1 = (9; 10; 0); а2 = (1; -1; 2); а3 = (4,5; 3; 36/19);
б) b 1 = (2; 1; 0); b 2 = (3; 0; -1); b 3 = (0; 10; 11)..
5) Вычислить пределы:
а)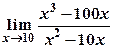 
; б)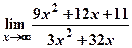 
.
6) Найти производную функции (y/x) и вычислить ее значение при x = 1:
а) y = ln (7х – 3) ; б)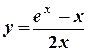 
; в) 
.
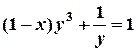7) Исследовать функцию у = х(х2 – 3)+4 и построить ее график.
8) Изобразить на плоскости xOy область определения функции двух переменных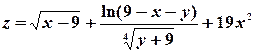 
.
9) Найти 
, если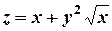 
.
10) Найти стационарные точки и исследовать на экстремум функцию
z = 0,5 x 2 + 2 xy + 0,5 y 2 – 4 x – 5 y .
Вариант 10.
1) Решить систему уравнений. Сделать проверку.
2 x + 4 y + 5 z = 25 ,
4 x + 5 y + 2 z = 16 ,
5 x – 2 y – 4 z = 4 .
2) Записать в виде системы линейных уравнений и решить эту систему методом Гаусса. Сделать проверку.
(х1 х2 х3)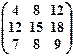 
= (0 0 0).
3) Построить бюджетное множество, отражающее покупательные возможности потребителя двух товаров по цене 105 и 70 руб., если на их приобретение можно израсходовать не более 4200 руб. а первого товара имеется не более 20 единиц.
4) Выяснить, какая из систем векторов линейно независима, и разложить по ней вектор р = (20,6; 11; 1):
а) а1 = (10; 5; 0); а2 = (1; -1; 2); а3 = (5; 3; -2/3);
б) b 1 = (2; 1; 0); b 2 = (3; 0; -1); b 3 = (0; 5; 6).
5) Вычислить пределы:
а)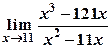 
; б)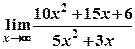 
.
6) Найти производную функции (y/x) и вычислить ее значение при x = – 1:
а) y = ln (х2 – 4х) ; б) 
; в) 
.
7) Исследовать функцию у =3х – х3 – 2 и построить ее график.
8) Изобразить на плоскости xOy область определения функции двух переменных 
.
9) Найти 
, если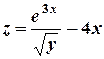 
.
10) Найти стационарные точки и исследовать на экстремум функцию
z = 2 xy – 3 x 2 – 2 y 2 + 10 .
Дата: 2019-05-28, просмотров: 449.
