Термодинамические системы - макроскопические объекты (тела и поля), которые могут обмениваться энергией как друг с другом, так и с внешней средой.
Термодинамическими параметрами или параметрами состояния системы являются физические величины, служащие для описания состояния термодинамической системы (давление, объем, масса, объем и температура).
Равновесным состоянием (состоянием термодинами ческого равновесия) называется состояние системы, не изменяющееся с течением времени.
Во всех частях термодинамической системы, находящейся в состоянии термодинамического равновесия, температура одинакова. При соприкосногвении двух тел с различной температурой происходит теплопередача от тела с большей температурой к телу с меньшей температурой.
Термодинамическим процессом называется изменение состояния термодинамической системы, происходящее при изменении какого-либо из внешних параметров системы.
Изопроцессами[11] называются термодинамические процессы, происходящие в системе с постоянной массой при каком-либо одном постоянном параметре состояния (давлении, объеме, температуре).
Изотермический (изотермный) процесс происходит при постоянной температуре (Т =const). Для данной массы газа: 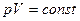 или
или 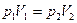 .
.
Изохорический (изохорный) процесс происходит при постоянном объеме ( V = const). Для данной массы газа: 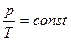 или
или 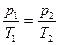 .
.
Изобарический (изобарный) процесс протекает при постоянном давлении (p=const). Для данной массы газа: 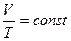 или
или 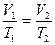 .
.
Адиабатным (адиабатическим) процессом называется термодинамический процесс, который происходит в системе без теплообмена с внешними телами ( 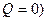 .
.
|
|
|
|
Уравнением состояния называется зависимость равновесного давления р в системе от объема и температуры: p = f ( V , T ):
| Термодинамика | Статистическая физика |
Уравнение состояния в термодинамике получается опытным путем.
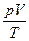 = const или = const или 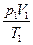 = = 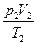 - уравнение Клапейрона[12]: для данной массы идеального газа отношение произведения численных значений давления и объема к абсолютной температуре есть величина постоянная - уравнение Клапейрона[12]: для данной массы идеального газа отношение произведения численных значений давления и объема к абсолютной температуре есть величина постоянная
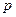 - давление, [Па];
V - объем, [ м3];
Т - абсолютная температура, [К] (Кельвин[13])
или - давление, [Па];
V - объем, [ м3];
Т - абсолютная температура, [К] (Кельвин[13])
или 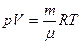 - уравнение Менделеева [14]-Клапейрона, где - уравнение Менделеева [14]-Клапейрона, где
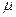 - молярная масса, [кг/моль];
m – масса газа, [кг]; - молярная масса, [кг/моль];
m – масса газа, [кг];
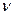 - количество вещества, [моль];
R = 8,31 Дж/(моль∙ К) – универсальная газовая постоянная; рассчитывается исходя из того, что при нормальных условиях (T=273,15 К, р=1,0132∙105 Па=1 атм=760 мм рт. ст.) моль любого газа имеет объем - количество вещества, [моль];
R = 8,31 Дж/(моль∙ К) – универсальная газовая постоянная; рассчитывается исходя из того, что при нормальных условиях (T=273,15 К, р=1,0132∙105 Па=1 атм=760 мм рт. ст.) моль любого газа имеет объем 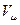 = 22,4 ∙10-3 м3 R= = 22,4 ∙10-3 м3 R= 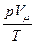 = 8,31 Дж/(моль∙ К) = 8,31 Дж/(моль∙ К)
| Уравнение состояния выводится теоретически
 , ,
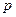 - давление, [Па] (Паскаль); - давление, [Па] (Паскаль);
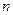 - концентрация молекул, [м-3];
k = 1,38×10-23 Дж/К - постоянная Больцмана[15] физическая величина, равная отношению универсальной газовой постоянной к постоянной Авогадро, т. е. - концентрация молекул, [м-3];
k = 1,38×10-23 Дж/К - постоянная Больцмана[15] физическая величина, равная отношению универсальной газовой постоянной к постоянной Авогадро, т. е.
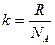 , k = 1,38×10-23 Дж/К. , k = 1,38×10-23 Дж/К.
|
2.1.Какой газ называется идеальным?
2.2.Какое выражение называется уравнением состояния идеального газа?
2.3.Определите число атомов в 1 кг водорода и массу одного атома водорода. [6,02∙1026; 1,5∙10-27кг]
2.4.Сколько молекул содержится в 1 см3 воды? [3,3∙1019]
2.5.Оцените объем одной молекулы воды и ее линейные размеры. [3∙10-29 м 3; 3∙10-10 м]
2.6.Определите плотность воздуха при нормальных условиях. Какая часть объема воздуха приходится на сами молекулы, если молекула воздуха имеет объем 3∙10-29 м 3? [1,28 кг/м3; 8∙10-4]
2.7.В сосуде объемом 15 л содержится 1,8∙1024 молекул газа при температуре 300 К. Определите давление газа, считая его идеальным. [500 кПа]
2.8.При нагревании идеального газа на 1 К при постоянном давлении объем его увеличился на 1/350 первоначального объема. Найдите начальную температуру газа [350 К]
2.9.В баллоне вместимостью 25 л находится водород при температуре 290 К. После того как часть водорода израсходовали, давление в баллоне понизилось на 0,4 МПа. Определите массу m израсходованного водорода. [8,3 г]
2.10. В сосуде вместимостью 5 л находится 0,2 моля газа. Определите, какой это газ, если его плотность равна 1,12 кг/м3. [азот]
2.11.В сосуде находится смесь 10 г углекислого газа и 15 г азота. Найдите плотность этой смеси при температуре 27°С и давлении 1,5∙105 Па [1,98 кг/м3]
2.12.В закрытом сосуде вместимостью 20 л при температуре 300 К находятся водород массой 6 г и гелий массой 12 г. Определите: 1)давление, 2) молярную массу газовой смеси.[0,75 МПа; 3∙10-3 кг/моль ]
2.13. Определите молярную массу смеси кислорода массой 25 г и азота массой 75 г. [28,9∙10-3 кг/моль]
Дата: 2019-04-23, просмотров: 269.
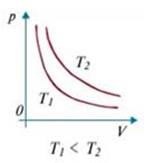 Изотерма
Изотерма
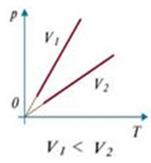 Изохора
Изохора
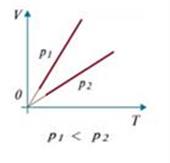 Изобара
Изобара
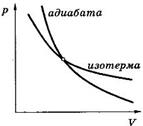 Адиабата и изотерма
Адиабата и изотерма