
Дифференцируя по времени линейную скорость:
 или
или  .
.
Каждая материальная точка вращающегося тела движется по окружности, при этом возникает нормальное (центростремительное) ускорение, направленное по радиусу вращения к центру (оси) вращения:
 = ω2 r.
= ω2 r.
1.1.Какая величина называется[1]:
а) средней скоростью движения,
б) средней путевой скоростью движения,
в) мгновенной скоростью движения,
г) ускорением,
д) угловой скоростью,
е) угловым ускорением?
1.2.Как связаны линейные и угловые кинематические параметры?
1.3.Частица из состояния покоя начала двигаться по дуге окружности радиуса с постоянным угловым ускорением. Чему равно отношение нормального ускорения к тангенциальному через одну секунду поле начала наблюдения?
1.4.Движение материальной точки в плоскости xy записывается уравнениями: x = ct 2 ; y = bt 2, где с и b – положительные постоянные. Найдите: 1) уравнение траектории точки y ( x ), 2) закон изменения радиус-вектора и модуля радиус-вектора, 3) закон изменения скорости и модуля скорости точки в зависимости от времени, 4) закон изменения ускорения тела. [1)y = bx / c; 2) 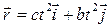 ;
; 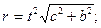 3)
3)  ;
;  4)
4)  ;
; 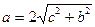 ]
]
1.5.Закон движения материальной точки имеет вид: х=А+ Bt + Ct 2 + Dt 3 ,где А=2 м, В=3 м/ c, C=0,14 м/с2, D = 0,01 м/с3. Через сколько времени после начала движения ускорение тела будет равно 1 м/с2? [12 с]
1.6.Две материальные точки движутся согласно уравнениям: х1=А1+ B 1 t + C 1 t 2 + + D 1 t 3 и х2 = А2+ B 2 t + C 2 t 2 + D 2 t 3 , где А 1=2 м; В 1=4 м/c; C 1=4 м/с2; D 1=-3 м/с3; А 2=2м; В 2=2 м/ c; C 2=-2 м/с2; D 2=1 м/с3. В какой момент времени ускорения этих точек будут одинаковы? [0,5 с]
1.7.По прямой линии движутся две материальные точки согласно уравнениям: x 1 = А1+ B 1 t + C 1 t 2 и x 2 = А2 + B 2 t + C 2 t 2, где А1 = 10 м; B 1=1м/с; C 1= 2 м/с2; А2=3 м; В2=2 м/с; С2 = 0,2 м/с2. В какой момент времени скорости этих точек будут одинаковы? Найдите ускорения точек в момент времени t=3 с.
1.8.Частица движется так, что радиус-вектор зависит от времени по закону:  , где с=3 м/с и b=1 м/с2,
, где с=3 м/с и b=1 м/с2,  и
и  - орты осей x и у. Найдите: 1) уравнение траектории точки; 2) модуль ее скорости; 3) модуль ускорения в момент времени t = 2 с. [1)
- орты осей x и у. Найдите: 1) уравнение траектории точки; 2) модуль ее скорости; 3) модуль ускорения в момент времени t = 2 с. [1)  ; 2)
; 2)  ; 3) 2 м/с2]
; 3) 2 м/с2]
1.9. Закон движения материальной точки, движущейся вдоль прямой, имеет вид х= bt – ct 2 , где b =40 м/с; с=4 м/с2. Найдите время и путь точки до полной остановки. [5 с ]
1.10.Частица движется в плоскости ху из точки x = y =0 со скоростью  , где А и В – положительные постоянные. Найдите: 1) зависимость координат точки от времени х( t ) и у( t ), 2) уравнение траектории частицы. [1)x =А t; y = Bt; 2) у = Bx / A]
, где А и В – положительные постоянные. Найдите: 1) зависимость координат точки от времени х( t ) и у( t ), 2) уравнение траектории частицы. [1)x =А t; y = Bt; 2) у = Bx / A]
1.11.Частица начинает движение из начала координат с ускорением, меняющимся по закону 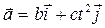 , где b и c -положительные постоянные. Определите уравнение траектории частицы.
, где b и c -положительные постоянные. Определите уравнение траектории частицы.
1.12.Точка движется, замедляясь по прямой, с ускорением, модуль которого зависит от скорости по закону  , где b = 1
, где b = 1  . B начальный момент времени скорость точки
. B начальный момент времени скорость точки  0 = 9 м/с. Сколько времени будет двигаться точка до полной остановки? Чему будет равен пройденный путь?
0 = 9 м/с. Сколько времени будет двигаться точка до полной остановки? Чему будет равен пройденный путь?
1.13.Колесо радиусом 0,1 м вращается так, что зависимость угла поворота радиуса колеса от времени дается уравнением 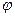 = А+ Bt + Ct 3 , где А = 4 рад; В=2 рад/с; С=1 рад/с3. Для точки, лежащей на ободе колеса, найдите через 3 с после начала движения: 1) угловую скорость; 2) линейную скорость; 3) угловое ускорение; 4) нормальное ускорение; 5) тангенциальное ускорение; 6) полное ускорение. 7) определите угол, который образует вектор полного ускорения с радиусом колеса. [1) 29 рад/ c; 2) 2,9 рад/с; 3) 18 рад/ c 2; 4) 84,1 м/ c 2; 5) 1,8 м/ c 2; 6) 84,12 м/ c 2; 7) 1,22˚]
= А+ Bt + Ct 3 , где А = 4 рад; В=2 рад/с; С=1 рад/с3. Для точки, лежащей на ободе колеса, найдите через 3 с после начала движения: 1) угловую скорость; 2) линейную скорость; 3) угловое ускорение; 4) нормальное ускорение; 5) тангенциальное ускорение; 6) полное ускорение. 7) определите угол, который образует вектор полного ускорения с радиусом колеса. [1) 29 рад/ c; 2) 2,9 рад/с; 3) 18 рад/ c 2; 4) 84,1 м/ c 2; 5) 1,8 м/ c 2; 6) 84,12 м/ c 2; 7) 1,22˚]
1.14.Материальная точка вращается вокруг неподвижной оси по закону  =А+ + Bt + Ct 3, где А=10 рад, В=20 рад/с; С=-2 рад/с3. Радиус окружности, на котором вращается точка, равен 0,1 м. Определите полное ускорение точки в момент времени t=1 с.
=А+ + Bt + Ct 3, где А=10 рад, В=20 рад/с; С=-2 рад/с3. Радиус окружности, на котором вращается точка, равен 0,1 м. Определите полное ускорение точки в момент времени t=1 с.
1.15.Точка находится на ободе колеса радиусом 0,5 м, вращающегося согласно уравнению 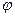 =Bt + Ct 3, где В=2 рад/с, С=0,2 рад/с3. Найдите полное ускорение точки в момент времени t = 3 c.
=Bt + Ct 3, где В=2 рад/с, С=0,2 рад/с3. Найдите полное ускорение точки в момент времени t = 3 c.
1.16.Тело вращается вокруг неподвижной оси Z так, что угол его поворота меняется в зависимости от времени по закону 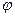 =2π( at–bt2/2), где а и b - положительные постоянные. Найдите: 1) момент времени t , в который тело останавливается; 2) число оборотов N тела до остановки.[1) t = a / b ;2) N = a 2 /2 b].
=2π( at–bt2/2), где а и b - положительные постоянные. Найдите: 1) момент времени t , в который тело останавливается; 2) число оборотов N тела до остановки.[1) t = a / b ;2) N = a 2 /2 b].
1.17.Колесо радиусом 10 см вращается с постоянным угловым ускорением 3,14рад/с2. Найдите для точек на ободе колеса к концу первой секунды после начала движения: 1) угловую скорость, 2) линейную скорость, 3) тангенциальное ускорение, 4) нормальное ускорение, 5) полное ускорение, 6) угол между направлением полного ускорения и радиусом колеса. [1) 3,14 рад/с; 2)0,314 м/с; 3) 0,314 м/с2; 4) 0,986 м/с2; 5) 1,03 м/с2; 6)17˚46'].
1.18.Нормальное ускорение точки, движущейся по окружности радиусом 4 м, задается уравнением а n=А+Bt+Ct 2 (А=1 м/с2, В=6 м/с2, С=9 м/с2). Определите: 1) тангенциальное ускорение точки; 2) путь, пройденный точкой за 5 с после начала движения; 3) полное ускорение через 1 с после начала наблюдения.
1.19.Точка вращается с угловой скоростью  , где А= 0,5 рад/с2; В=0,06 рад/с3. Найдите модули угловой скорости и углового ускорения в момент времени t=10 c.
, где А= 0,5 рад/с2; В=0,06 рад/с3. Найдите модули угловой скорости и углового ускорения в момент времени t=10 c.
1.20.Точка начинает вращаться вокруг неподвижной оси с угловым ускорением  = kt , где k = 4 рад/с3. Определите угловую скорость точки в момент времени t = 2 с.
= kt , где k = 4 рад/с3. Определите угловую скорость точки в момент времени t = 2 с.
1.21. Материальная точка начинает двигаться по окружности радиусом 12,5 см с постоянным тангенциальным ускорением 0,5 см/с2. Определите: 1) момент времени, при котором вектор полного ускорения образует с вектором скорости угол 45˚; 2)путь, пройденный за это время движущейся точкой. [1)5 с;2)6,25с м]
1.22.Точка движется по окружности длиной 1,57 м с линейной скоростью 10 см/с. Полное ускорение точки 0,05 м/с2. Чему равно ее тангенциальное ускорение? Найдите угол между векторами полного и тангенциального ускорений. [0,03 м/с2; 53°].
1.23.Точка движется по плоскости так, что ее тангенциальное ускорение не изменяется и равно aτ= 4 м/с2, а нормальное ускорение зависит от времени по закону an=bt 4, где b=2 м/с6. Найдите радиус кривизны траектории в момент времени t=2 с, если в момент начала наблюдения точка покоилась.
1.24.Точка движется по окружности радиусом 4 м так, что в каждый момент времени ее нормальное и тангенциальное ускорений равны по модулю. В начальный момент времени t=0 скорость точки равна 0,2 м/с. Найдите скорость точки в момент времени t=10 с.
1.25. Закон движения точки, лежащей на ободе колеса, катящегося равномерно по горизонтальному пути (оси ОX ), имеет вид: x =А(ω t – sinωt ); y =(1- cos ωt ), где A=5 м. Найдите путь, пройденный точкой за время  .
.
1.26.Ось с двумя дисками, расположенными на расстоянии 0,5 м друг от друга, вращается с частотой 1600 об/мин. Пуля, летящая вдоль оси, пробивает оба диска; при этом отверстие от пули во втором диске смещено относительно отверстия в первом диске на угол 12°. Найдите скорость пули. [400 м/с]
1.27.Найдите радиус вращающегося колеса, если известно, что линейная скорость точки, лежащей на ободе, в 2,5 раза больше линейной скорости точки, лежащей на 5 см ближе к оси колеса. [8,33 см]
1.28.Колесо, вращаясь равноускоренно, достигло угловой скорости 20 рад/с через 10 оборотов после начала вращения. Найти угловое ускорение колеса. [3,2 рад/с2]
1.29.Колесо, вращаясь равноускоренно, через 1 мин после начала вращения, приобретает частоту 720 об/мин. Найдите угловое ускорение колеса и число оборотов колеса за эту минуту. [1,26 рад/с2; 360 об]
1.30.Колесо, вращаясь равнозамедленно, при торможении уменьшило свою частоту за 1 мин с 300 об/мин до 180 об/мин. Найдите угловое ускорение колеса и число оборотов, сделанных им за это время. [0,21 рад/с2; 240 об]
РАЗДЕЛ 2. ДИНАМИКА
Основные формулы
| Динамика материальной точки и поступательного движения твердых тел | Динамика вращательного движения твердых тел |
Сила 
| Момент силы  ; ; 
|
Импульс 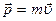
| Момент импульса 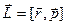 ; ; 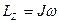
|
| Масса m | Момент инерции  ; ; 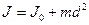
|
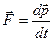
| 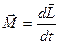
|
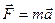
| 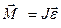 ; ; 
|
Силы природы
| всемирного тяготения | тяжести | упругости | трения (скольжения) |
| F = Gm 1 m 2/r2 | 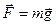
| Fx = -kx | F тр = m N |
Центр масс: 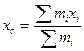
Дата: 2019-04-23, просмотров: 347.