| материальной точки | твердого тела | сплошного цилиндра (диска) | Полого цилиндра | однородного шара | однородного стержня |
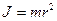
| 
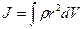
| 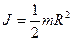
| 
|  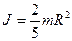
| 
|
Динамика материальной точки
|
Инерция - это свойство тела сохранять свою скорость движения неизменной (и по величине, и по направлению), когда на тело не действуют никакие силы.
Чтобы изменить скорость движения тела, на него необходимо подействовать с некоторой силой. Инертность - это свойство тел сопротивляться изменению их скорости.
Масса – это мера инертности тела (обозначается m, единицы [кг]).
Сила - физическая величина, являющаяся мерой механического взаимодействия тел. Сила считается заданной, если известны ее численное значение, направление и точка приложения.
Второй закон Ньютона: Второй закон Ньютона: ускорение, которое получает тело, прямо пропорционально равнодействующей всех приложенных к нему сил и обратно пропорционально его массе:
 .
.
|
 .
.
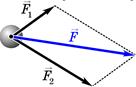
Равнодействующая сила – это сила, которая производит на тело такое же действие, как несколько одновременно действующих сил.
Второй закон Ньютона можно записать в другой форме: 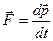 . Значит, сила действия на тело равна изменению импульса тела.
. Значит, сила действия на тело равна изменению импульса тела.
|
противопо ложные стороны, т. е.

Динамика твердого тела
|
 .
.
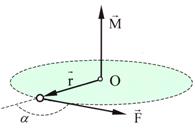
Момент силы характеризует способность силы вращать тело вокруг точки О.
 ; M = Frsina=Fl ,[Нм].
; M = Frsina=Fl ,[Нм].
где a - угол между векторами,
l = r sina - плечо силы - длина перпендикуляра, опущенного из точки О на линию действия силы.
|
Моментом импульса материальной точки относительно неподвижной точки О называется векторное произведение:
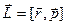 , L = rpsin a ., [
, L = rpsin a ., [  ].
].
Момент импульса характеризует возможность совершать вращательное движение.
Направление момента силы определяется правилом правого винта. Частица обладает моментом импульса независимо от формы траектории, по которой она движется.
Моментом импульса системы относительно неподвижной оси называется величина, равная проекции на эту ось вектора 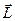 момента импульса системы относительно какой-либо точки, принадлежащей оси.
момента импульса системы относительно какой-либо точки, принадлежащей оси.
 .
.
|
 , [кг∙м2].
, [кг∙м2].
Момент инерции является мерой инертности тела при вращательном движении. Тело обладает моментом инерции независимо от того вращается оно или нет.
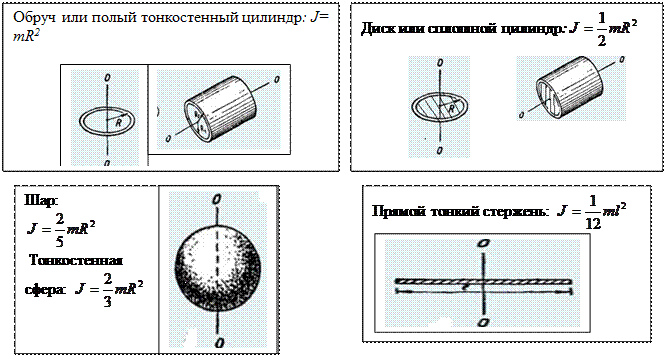
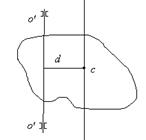
Момент инерции относительно других осей вращения . Теорема Штейнера (теорема о переносе осей инерции):
|
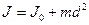 .
.
Основное уравнение динамики вращательного движения:
 .
.
Связь между моментом импульса и моментом инерции:
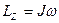 .
.
1.31.Какая величина называется[3]:
а) силой,
б) импульсом,
в) массой,
г) моментом силы относительно неподвижной точки и относительно оси,
д) моментом импульса относительно неподвижной точки и относительно оси,
е) моментом инерции?
1.32.Сформулируйте теорему Штейнера.
1.33. Напишите основное уравнение динамики поступательного движения.
1.34.Напишите основное уравнение динамики вращательного движения.
1.35.Как связаны момент силы, момент импульса и момент инерции?
1.36.Тело массой 2 кг движется прямолинейно по закону s=А-Bt +С t 2 - Dt 3 (С=2м/с2, D=0,4 м/с3). Определите силу, действующую на тело в конце первой секунды движения. [3,2 Н]
1.37.К нити подвешен груз массой 500 г. Определите силу натяжения нити, если нить с грузом: 1) поднимать с ускорением 2 м/с2; 2) опускать с ускорением 2м/с2. [1)5,9 Н; 2) 3,9 Н]
1.38. Тело массой m движется в плоскости xy по закону x=Acosωt, y = Bsinωt, где А, В и ω – некоторые постоянные. Определите модуль силы, действующей на это тело.[  ]
]
1.39. Частица массой m движется под действием силы F = F0cosωt, где F0 и ω – некоторые постоянные. Найдите зависимость радиус-вектора от времени, если в начальные момент времени r(0)=0 и 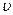 (0) =0. [
(0) =0. [  ]
]
1.40.Два груза (m1 =500 г и т2 = 700 г) связаны невесомой нитью и лежат на гладкой горизонтальной поверхности. К грузу т1 приложена горизонтально направленная сила 6 Н. Пренебрегая трением, определите: 1) ускорение грузов; 2) силу натяжения нити [1) 5 м/с2; 2) 3,5 Н]
1.41.Самолет, летящий со скоростью 360 км/ч, описывает вертикальную петлю Нестерова радиусом 360 м. Определите силу, прижимающую летчика массой 80 кг к сиденью: 1) в нижней точке этой петли, 2) в верхней точке этой петли. [1) 3 кН; 2) 1,44 кН]
1.42.Самолет летит в горизонтальном направлении с ускорением 20 м/с2. Какова перегрузка* пассажира, находящегося в самолете? [2,27]
1.43. К потолку вагона, движущегося в горизонтальном направлении с ускорением 9,81 м/с2, подвешен на нити шарик массой 200 г. Определите: 1)силу натяжения нити, 2) угол отклонения нити от вертикали. [1)2,77 Н; 2) 45˚]
1.44. Определите положение центра масс системы, состоящей из четырех шаров, массы которых равны соответственно m, 2m, 3m и 4m, в следующих случаях: 1) шары расположены на одной прямой; 2) шары расположены в вершинах квадрата; 3) шары расположены по четырем смежным вершинам куба. Во всех случаях расстояние между соседними шарами равно 15 см. [1) 30cм; 2) 7,5 см, 4,5 см; 3) 1,5 см, 4,5 см, 3 см]
1.45.Определите момент инерции тонкого однородного стержня длиной 50 см и массой 360 г относительно оси: 1) перпендикулярной стержню,проходящей через его центр; 2) проходящей через конец стержня; 3) проходящей через точку, отстоящую от конца стержня на 1/6 его длины. [1) 7,5∙10-3 кг∙м2; 2) 3∙10-2 кг∙м2; 3)1,75∙10-2 кг∙м2]
1.46. Четыре маленьких шарика одинаковой массы, жестко закрепленные невесомыми стержнями, образуют квадрат. Найдите отношение моментов инерции системы, если ось вращения совпадает со стороной квадрата J1 или с его диагональю J2.
1.47.Два шара радиусом r1 = r2 = 5 см закреплены на концах тонкого стержня, вес которого значительно меньше веса шаров. Расстояние между центрами шаров 0,5 м . Масса каждого шара 1 кг . Найдите: 1)момент инерции этой системы относительно оси, проходящей через середину стержня перпендикулярно его длине; 2) момент инерции этой системы относительно той же оси, считая шары материальными точками, массы которых сосредоточены в их центрах. [1) 63,5∙10-3 кг∙м2 ; 2) 62,5∙10-3 кг∙м2 ]
1.48.К ободу однородного диска радиусом 0,2 м приложена постоянная касательная сила 98,l Н. При вращении на диск действует момент сил трения 5 Н∙м. Найдите массу диска, если известно, что диск вращается с постоянным угловым ускорением 100 рад/с2.[7,3 кг]
1.49.Шар радиусом 10 см и массой 5 кг вращается вокруг оси симметрии согласно уравнению φ=А+ Bt 2 + Ct 3 (В=2 рад/с2,C=-0,5 рад/с3). Определите момент сил при t = 3 с [- 0,1 Н∙м].
1.50.Однородный диск радиусом 0,2 м и массой 5 кг вращается вокруг оси, проходящей через его центр. Зависимость угловой скорости вращения диска от времени дается уравнением ω= A + Bt , где В=8 рад/с2. Найдите величину касательной силы, приложенной к ободу диска. Трением пренебречь.
1.51.К ободу колеса, имеющего форму диска, радиусом 0,5 м и массой 50 кг приложена касательная сила в 100 Н. Найдите: 1) угловое ускорение колеса, 2) через сколько времени после начала действия силы колесо будет иметь скорость, соответствующую 100 об/с?
1.52.На барабан массой 9 кг намотан шнур, к концу которого привязан груз массой 2 кг . Найдите ускорение груза. Барабан считать однородным цилиндром. Трением пренебречь.[3 м/с2]
1.53. Две гири массой 2 кг и 1 кг соединены нитью и перекинуты через блок массой 1 кг . Найдите: 1) ускорение, с которым движутся гири; 2) натяжения нитей, к которым подвешены гири. Блок считать однородным диском. Трением пренебречь.[1)2,8 м/ c 2; 2)14 Н; 12,6 Н]
РАЗДЕЛ 3. ЗАКОНЫ СОХРАНЕНИЯ
Основные формулы
| Поступательное движение | Вращательное движение |
Закон сохранения

 = const,
= const, 
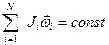
Работа

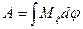
Мощность 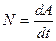 ; <N> =
; <N> = 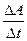
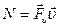

Кинетическая энергия
 ;
; 
 ;
; 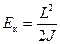
Eк=  +
+ 
 Потенциальная энергия: Ep(x,y,z) = -Aконс*.
Потенциальная энергия: Ep(x,y,z) = -Aконс*.  **
**
| в однородном поле сил тяжести | деформированной пружины |
| Ep=mgh | Ep =kx2/2 |
Теорема о кинетической энергии: А = ΔEк. Теорема о потенциальной энергии: А = - Δ Ep
Полная энергия: E =Eк + Ep
| Величина | Единица | ||
| Обозначение | Наименование | ||

| импульс материальной точки | кг∙м/с | кг∙м/с |
| m | масса | кг | кг |
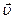
| скорость | м/с | м/с |

| сила | Н (ньютон) | кг∙м/с2 |

| ускорение | м/с2 | м/с2 |
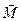
| момент силы относительно неподвижной точки | Н∙м | кг∙м2/с2 |

| момент силы относительно оси z | Н∙м | кг∙м2/с2 |
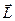
| момент импульса материальной точки относительно неподвижной точки | кг∙м2/с | кг∙м2/с |
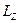
| момент импульса твердого тела относительно неподвижной точки | кг∙м2/с | кг∙м2/с |
| J | момент инерции | кг∙м2 | кг∙м2 |
| ω | угловая скорость | рад/с | рад/с |
| r | расстояние от точки до оси | м | м |
| ε | угловое ускорение | рад/с2 | рад/с2 |
| d | расстояние от центра тяжести тела до оси вращения | м | м |
| R | радиус | м | м |
| l | длина стержня | м | м |

| ускорение свободного падения | м/с2 | м/с2 |
| k | жесткость | Н/м | кг/ с2 |
| х | абсолютная деформация | м | м |
| μ | коэффициент трения | ||
| N | сила нормального давления | Н (ньютон) | кг∙м/с2 |
| А | механическая работа | Дж (джоуль) | кг∙м2/ с2 |
| E к | кинетическая энергия | Дж (джоуль) | кг∙м2/ с2 |
| N | мощность | Вт (ватт) | кг∙м2/ с3 |
| <N> | средняя мощность | Вт (ватт) | кг∙м2/ с3 |
| Ep | потенциальная энергия | Дж (джоуль) | кг∙м2/ с2 |
| Е | полная энергия | Дж (джоуль) | кг∙м2/ с2 |
G = 6,67×10–11 Н∙м2/кг2 – гравитационная постоянная.
Для замкнутых[4] систем остаются постоянными (сохраняются) три физические величины: энергия, импульс и момент импульса. Соответственно имеются три закона сохранения: закон сохранения энергии, закон сохранения импульса и закон сохранения момента импульса. Эти законы тесно связаны со свойствами времени и пространства.
|
Закон сохранения импульса: импульс замкнутой системы не изменяется с течением времени:
 , следовательно,
, следовательно,  =
=  ,
,  =
= 
|
1. Если сумма внешних сил равна нулю.
2. В некоторых процессах (например, при ударе или выстреле) импульсы частей системы претерпевают большие изменения за сравнительно короткие промежутки времени.
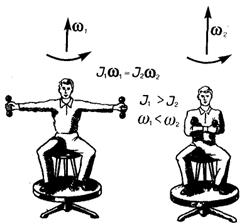
Закон сохранения момента импульса: момент импульса замкнутой системы не изменяется с течением времени:
 = const,
= const, 
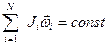 .
.
Дата: 2019-04-23, просмотров: 325.