Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Механической работой называют работу силы над телом, в результате действия которой тело перемещается.

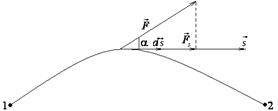
Элементарной работой силы на малом перемещении называется скалярная величина 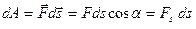, [Дж[5]].

Если 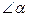 - острый, то A>0;

если 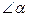 - тупой, то A<0;

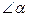если кратен 90˚, то А=0.

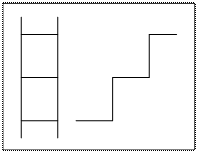
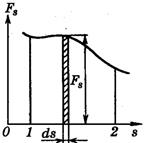
Работу, совершаемую на пути можно определить по площади фигуры под графиком силы.

Работа силы на пути равна:

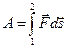, следовательно, если сила не изменяется, то A = Fs cos a .

При вращательном движении твердого тела .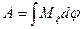

Мощность – физическая величина, показывающая работу, совершаемую в единицу времени 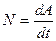, [Вт[6]].

Следовательно:

1)средняя мощность <N> = ;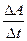

2)учитывая, что 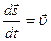, получим: 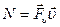, то есть мощность равна скалярному произ­ведению силы на скорость точки приложения силы.

3)Мощность при вращении твердого тела: 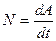= 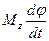, но т.к. направления оси z и ω совпадают, то N = .

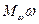В технике иногда применяется единица мощности, именуемая лошадиной силой (л. с.) и равная 736 Вт.

 

Консервативные и диссипативные силы

Консервативными силами называются:

1) силы, работа которых не зависит от пути, по кото­рому двигалась частица, а зависит лишь от началь­ного и конечного положений частицы; 2)работа консервативных сил на любом замкнутом пути равна нулю.

Диссипативные силы – силы:

1) суммарная работа которых при любых перемещениях замкнутой системы всегда отрицательна (сила трения скольжения, сила сопротивления движению),

2) зависят от взаимного расположения тел и от их относительных скоростей.

Механическая энергия

 - это энергия, связанная с движением объекта или его положением, способность совершать механическую работу.

Механическая энергия описывает сумму потенциальной и кинетической энергий.

Кинетическая энергия тела (от греческого слова kinema - движение)  – это энергия его механического движения: E_к= 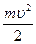 или .

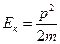Кинетическая энергия вращающегося тела:

E_к = 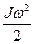 или .

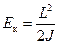Кинетическая энергия катящегося вращающегося твердого тела

E_к= + .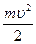

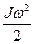Теорема о кинетической энергии: изменение кинетической энергии равно работе результирующей всех сил: Δ E _к =А или А = Δ E _к.

Потенциальная энергия (от латинского potentia - возможность)– это энергия взаимодействия тел или частей одного и того же тела.

Поясняющий рисунок

Потенциальная энергия тела, поднятого над нулевым уровнем:

E_p = mgh    

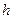 - высота, [м];                                                

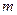 - масса, [кг];

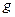 - ускорение свободного падения, [ ].      

Поясняющий рисунок

Потенциальная энергия деформированной пружины:

 

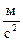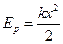
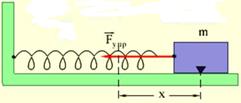
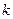 – жесткость, ;

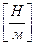 x – абсолютная деформация тела, [м].

Теорема о потенциальной энергии: работа консервативных сил равна убыли потенциальной энергии: А = - Δ E_p .

Потенциальная энергия может быть как положительной, так и отрицательной.

Закон сохранения полной механической энергии : полная механическая энер­гия частицы, движущейся в поле консервативных сил, остается постоянной.

Е _{p 1} + Е _{k 1} = Е_р2+Е _{k 2} .

При наличии диссипативных сил полная меха­ническая энергия системы не сохраняется. При их наличии сил трения и сил сопротивления среды полная механическая энергия системы уменьшается, переходя во внутреннюю энергию тел, что приводит к их нагреванию. Такой процесс называется дисси­пацией энергии (латинское слово «диссипация» означает «рассеяние»).

 

1.54.Конькобежец массой 70 кг, стоя на коньках на льду, бросает в горизонтальном направлении камень массой 3 кг со скоростью 8 м/с. Найдите, на какое рас­стояние откатится при этом конькобежец, если известно, что коэффициент трения коньков о лед равен 0,02.

1.55.Тело массой 3 кг движется со скоростью 3 м/с и нагоняет второе тело массой 3 кг , движущееся со скоростью 1 м/сек. Найдите скорости тел после столкновения, если: 1) удар был неупругий, 2) удар был упругий. Тела движутся по одной прямой. Удар - цен­тральный. Каково должно быть соотношение между мас­сами тел предыдущей задачи, чтобы при упругом ударе первое тело после удара остановилось?[1) 1,8 м/ c, 0,6 м/с; 2) 0,6 м/с, 2,6 м/с; 1/3]

1.56.Тело массой 3 кг движется со скоростью 4 м/с и ударяется о неподвижное тело такой же массы. Считая удар центральным и неупругим, найдите количе­ство тепла, выделившееся при ударе.[12 Дж]

1.57. Два шара подвешены на параллельных нитях одинаковой длины так, что они соприкасаются. Масса первого шара 0,2 кг , масса второго 100 г . Первый шар отклоняют так, что его центр тяжести поднимается на высоту 4,5 см , и отпускают. На какую высоту подни­мутся шары после соударения, если:                 1) удар упругий, 2) удар неупругий?[1) 5 мм; 8 см; 2) 2 см]

1.58.Диск массой 2 кг и радиусом 10 см катится без скольжения по горизон-тальной плоскости со скоростью 4 м/с. Найдите кинетическую энергию диска.

1.59.Шар диаметром 6 см катится без скольжения по горизонтальной плос-кости, делая 4 об/с. Масса шара 0,25 кг . Найдите кинетическую энергию шара.

1.60.Шар массой 1 кг и радиусом 10 см , катящийся без скольже­ния, ударяется о стенку и откатывается от нее. Скорость шара до удара о стенку 10 см/с, после удара 8 см/с. Найдите количество тепла Q, выделившееся при ударе.

1.61.Диск массой 1 кг и диаметром 60 см вращается вокруг оси, проходящей через центр перпендикулярно его плоскости, делая 20 об/с. Какую работу надо совершить, чтобы остановить диск? [355 Дж]

1.62.Кинетическая энергия вала, вращающегося с постоянной скоростью, соответствующей 5 об/с, равна 60 Дж. Найдите момент импульса этого вала.

1.63.Найдите линейные ускорения движения центров тяжести: 1) шара, 2) диска и 3) обруча, скатывающихся без скольжения с наклонной плоскости. Угол наклона плоскости равен 30°, начальная скорость всех тел равна нулю.               [1) 3,5 м/с²; 2) 3,27 м/с²; 3) 2,44 м/с²]

1.64.Колесо, вращаясь равнозамедленно при тормо­жении, уменьшило за 1 мин скорость вращения от 300 до 180 об/мин. Момент инерции колеса равен 2 кг∙м². Найдите: 1) угловое ускорение колеса, 2) тормозящий момент, 3) работу торможения, 4) число оборотов, сделанных колесом за эту минуту.

1.65.Маховое колесо начинает вращаться с постоянным угловым ускорением 0,5 рад/с² и через 15 с после начала движения приобретает момент импульса,  равный 73,5 кг∙м²/с. Найдите кинетическую энергию колеса через 20 с после начала вращения. [490 Дж]

1.66.Мальчик катит обруч по горизонтальной доро­ге со скоростью 7,2 км/ч . На какое расстояние может вкатится обруч на горку за счет его кинетической энер­гии? Уклон горки равен 10 м на каждые 100 м пути, если момент инерции обруча равен 2 кг∙м².

1.67.Платформа в виде сплошного диска радиусом 1,5 м и массой 180 кг вращается около вертикальной оси с частотой 10 об/мин. В центре платформы стоит человек массой 60 кг. Какую линейную скорость относительно пола помещения будет иметь человек, если он перейдет на край платформы? [1 м/с]

1.68.Человек, стоящий на скамье Жуковского, держит в руках стержень длиной 2,5 м и массой 8 кг, расположенный верти­кально вдоль оси вращения скамейки. Эта система (скамья и человек) обладает моментом инерции 10 кг∙м² и вращается с частотой 12 об/мин. Определите частоту вращения системы, если стер­жень повернуть в горизонтальное положение. [8,5 об/мин]

1.69.Платформа, имеющая форму сплошного однородного дис­ка, может вращаться по инерции вокруг неподвижной вертикальной оси. На краю платформы стоит человек, масса которого в 3 раза меньше массы платформы. Определите, как и во сколько раз изменит­ся угловая скорость вращения платформы, если человек перейдет ближе к центру на расстояние, равное половине радиуса платформы. [Возрастет в 1,43 раза].