равна сумме кинетических энергий его молекул (так как потенциальная энергия взаимодействия молекул идеального газа равна нулю) 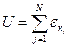 .
.
Закон равномерного распределения энергии по степеням свободы: на каждую степень свободы молекулы в среднем приходится одинаковая кинетическая энергия, равная
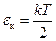 ,
,
Числом степеней свободы механической системы называется количество независимых величин, с помощью которых может быть задано положение молекулы в пространстве.
В механике определяется поступательное, вращательное и колебательные движения.
1)Одноатомная молекула газа движется только поступательно, поэтому: i =3.
2)Двухатомная молекула газа с жесткой связью может двигаться не только поступательно (i п =3), но и совершать вращательные движение вокруг осей О1-О1 и О2-О2 (i вр =2). Следовательно,
i = i п + i вр =3+2=5.
3)Трех атомная молекула газа (многоатомная молекула) имеет i =6 степеней свободы.

Внутренняя энергия многоатомного газа 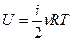

Покажем это. Внутренняя энергия идеального газа представляет собой кинетическую энергию всех видов движения его частиц
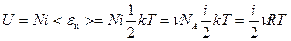 .
.
Теплоемкости газов 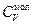 =
= 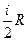 - молярная теплоемкость газа при постоянном объеме.
- молярная теплоемкость газа при постоянном объеме.
и 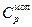 =
= 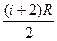 - молярная теплоемкость газа при постоянном давлении.
- молярная теплоемкость газа при постоянном давлении.
Покажем это. Молекулы газа имеют i степеней свободы, и 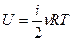 . Исходя из Iзакона термодинамики
. Исходя из Iзакона термодинамики 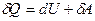 , для изохорного процесса
, для изохорного процесса 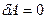 ,
, 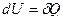 , т.е.
, т.е. 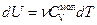 . Для одного моля
. Для одного моля 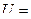
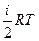 .
. 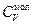 =
= 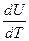 =
= 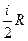 . Согласно формуле Майера
. Согласно формуле Майера 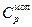 =
= 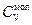 +
+ 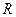 =
= 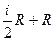 =
= 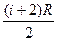 .
.
Закон распределения молекул идеального газа по скоростям (закон распределения Максвелла)
определяет, какое число dN молекул однородного одноатомного идеального газа из общего числа N его молекул в единице объема имеет при данной температуре скорости, заключенные в интервале от 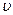 до
до 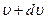 .
.
Закон применим для газов в состоянии термодинамического равновесия.
Распределение молекул такого газа по скоростям является стационарным.
|
Функция распределения Максвелла может быть представлена в виде:
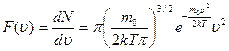
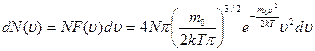
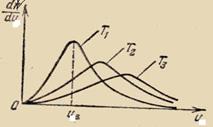
Из кривых распределения молекул по скоростям при различных температурах Т1<Т2<Т3 видно, что
с повышением температуры наиболее вероятная скорость молекул возрастает, а доля молекул, обладающих этой скоростью, уменьшается.
Для функции Максвелла выполняется соотношение: 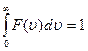 .
.
|
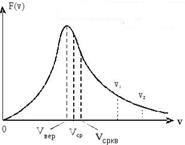
Наиболее вероятная скорость: 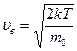 . Наиболее вероятной будет скорость, отвечающая максимуму
. Наиболее вероятной будет скорость, отвечающая максимуму 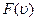 . Ее значение находят, приравняв производную
. Ее значение находят, приравняв производную 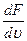 .
.
Средняя квадратичная скорость молекул: 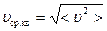 =
= 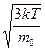 .
.
Средняя арифметическая скорость: 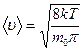 .
.
Дата: 2019-04-23, просмотров: 270.