Определение чисел зубьев:
1) Суммарное число зубьев ZΣ:
ZΣ = 2·aW· cos β / m ,(2.38)
где β – угол наклона линии зуба.
Величина ZΣ округляется до ближайшего целого числа.
2) Число зубьев шестерни Z1 :
Z1 = ZΣ / (u + 1).(2.39)
3) Число зубьев колеса Z2:
Z2 = ZΣ – Z1.(2.40)
4) Окружная скорость колёс v, м/с:
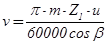.(2.41)
5) Уточнённое передаточное число u 21:
u 21 = Z2 /Z1.(2.42)
6) Ширина шестерни b2, мм:
b2 = 1,1 b2.(2.43)
7) Межосевое расстояние, мм:
aW = 0,5·m(Z1 + Z2) + (Х1 + X2 – Δy)m ,(2.44)
где Х1 , X2 – коэффициенты смещения (Х1 = X2=0 [2]); Δy – коэффициент уравнительного смещения (Δy = 0 [2]).
8) Угол наклона линии зуба для прямозубых колёс β = 0.
9) Делительные диаметры d, мм:
d = m · z / cos β.(2.45)
10) Диаметр вершин d a, мм:
d a = d + (2 + 2x– 2Δy)m.(2.46)
11) Диаметр впадин d f , мм:
d f = d – (2,5 – 2x)m.(2.47)
12) Окружная толщина зубьев по делительной окружности St, мм:
St = (π/(2cos β) + 2x·tgα)m.(2.48)
13) Угол зацепления αW:
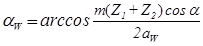,(2.49)
где α – угол профиля (α = 20˚).
14) Торцевой коэффициент перекрытия εα:
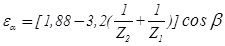.(2.50)
15) Коэффициент суммарной длины контактных линий Zε:
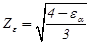.(2.51)
16) Угол наклона линии зуба по основной окружности βв:
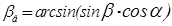.(2.52)
17) Коэффициенты формы сопряжённых поверхностей зубьев в полосе зацепления Zн:
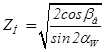.(2.53)
18) Рабочее контактное напряжение σн, мПа:
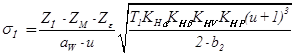,(2.53)
где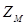 
- коэффициент, учитывающий механические свойства материалов сопрягаемых поверхностей ( 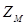= 275) [14].
19) Отклонение рабочего контактного напряжения от допускаемого ∆σн, %:
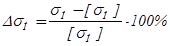.(2.54)
20) Окружное усилие Ft, H:
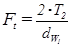,(2.55)
где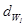 
- начальный диаметр колеса, мм.
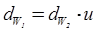,(2.56)
где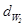 
- начальный диаметр шестерни, мм.
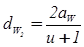.(2.57)
21) Радиальное усилие Fy, H:
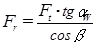. (2.58)
22) Осевое усилие Fa, H:
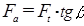.(2.59)
23) Коэффициент перекрытия зубьев Yε :
Yε=1.
24) Коэффициент наклона зубьев Yβ :
Yβ=1.
25) Рабочее изгибное напряжение зубьев шестерни σF2, мПа:
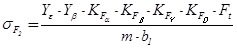.(2.60)
26) Рабочее изгибное напряжение колеса σF1, мПа:
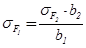.(2.61)
27) Максимальное контактное напряжение σн max, мПа:
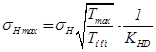.(2.62)
28) Максимальное изгибное напряжение σF max, мПа:
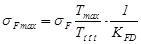.(2.63)
Значения рассчитываемых величин представлены на распечатках результатов расчёта, сделанного на ЭBM (программа ДМ-1).
2.3.3 Результаты расчёта зубчатой передачи, выданные ЭВМ
2.3.4 Анализ результатов расчёта зубчатой передачи
Геометрические параметры округляем до сотых долей миллиметра.
По допускаемым и рабочим напряжениям делаем вывод, что прочность достаточна.
Усилие в зацеплении округляем с точностью до целых.
Уточнённый расчёт валов и выбор подшипников
Данный расчёт даёт более достоверные результаты, чем ориентировочный расчёт.
В этом разделе исходными данными являются: силы, действующие на колесо шестерни, расстояния между линиями действия всех сил, диаметры колёс.
Для наглядного представления изобразим аксонометрическую схему нагружения валов (рисунок 2.9).
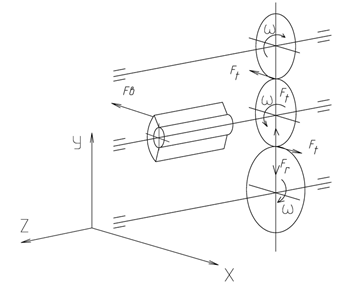
Рисунок 2.9 – Схема нагружения валов
Расчёт дебалансного вала
Для уточнённого расчёта выполним эскизную компоновку элементов вала (рисунок 2.10).
Предварительно назначаем подшипник по ГОСТ 5720 – 75: № 1608 с d=40 мм, D =90 мм, B =33 мм [2].
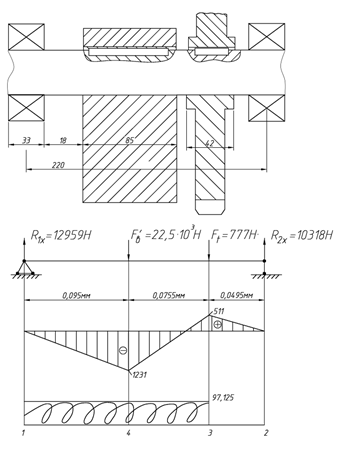
Рисунок 2.10 – Эскизная компановка элементов вала
На вал действуют две силы в направлении X (рисунок 2.10, б) F’в , Ft и крутящий момент T.
Составим уравнения суммы моментов относительно точек 1 и 2, найдём реакции в этих точках.
ΣM1=0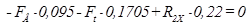 
;
.
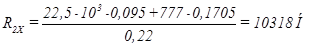ΣM2=0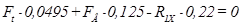 
;
.
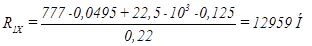Находим изгибающий момент в т. 1, 2, 3 ,4 (Рисунок 2.10, в):
;
;
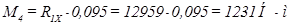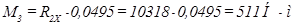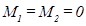
Максимальный изгибающий момент в т.4 под дебалансом.
Приведённый момент:
,(2.64)
где α – коэффициент учитывающий соответствие центров касательного и нормального напряжения (α = 0,75 [4]); T – крутящий момент, Н·м.
T =Ft·d/2 ,(2.65)
где d – делительный диаметр шестерни (d = 0,25 м);
T =777·0,25/2=91,125 Н·м.
.
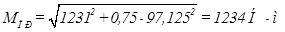Диаметр вала по формуле:
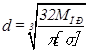,(2.66)
.
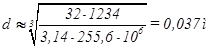Окончательно принимается диаметр вала d = 0,04 м.
Выбор подшипников
Ранее принятый подшипник (см. п.2.4.1) проверяем на динамическую грузоподъёмность:
Стабл. >Cрасч,(2.67)
где Стабл. – динамическая грузоподъёмность взятая из таблицы [3], (Стабл. = 44,9 кН); Cрасч. – динамическая грузоподъёмность полученная методом расчёта, кН.
Cрасч. = L1/P·P,(2.68)
где p – показатель степени (для шарикоподшипников p = 3 [2]); L – номинальный ресурс подшипников, млн. об.; P – эквивалентная нагрузка, Н.
L = Ln·60·nII /106,(2.69)
где Ln – номинальный ресурс в часах (примем Ln=125 ч)
L = 150·60·1800/106=16,2 млн.об.
Эквивалентная нагрузка, Н:
P = R·V·Kδ·KТ , (2.70)
где R – радиальная нагрузка, Н (R = 12959 Н); V – коэффициент вращения (V=1,[2] стр. 359) Kδ – коэффициент, учитывающий нагрузки (Kδ =1,35,[2] стр. 362 ); KТ – температурный коэффициент (KТ =1 [2]).
P = 12959·1·1,35·1=17494,65 H.
Срасч.=16,21/3·17494,65=44266,67 H.
Условие (2.67) выполняется. Окончательно принимаем для дебалансного вала шарикоподшипник радиальный сферический двухрядный (по ГОСТ 5720 – 75) [2]:
№ 1608 С=44,9 мм; d=40 мм; D=90 мм; B=33 мм.
Дата: 2019-05-28, просмотров: 230.
