Для дебалансного возбудителя рассчитывается требуемая вынуждающая сила FВ и, соответственно, конструкция дебалансов, обеспечивающих колебания виброплиты, с заданной амплитудой.
При вращении дебалансов с угловой частотой ω и амплитудой Sa суммарная вынуждающая сила составит:
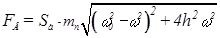, (2.10)
где mn – приведенная масса колеблющихся элементов, кг; ωo – частота свободных колебаний плиты с учётом жёсткости балласта, с-1; h – коэффициент демпфирования, с-1.
Находим mn:
mn = an ·m, (2.11)
где m –масса корпуса плиты с вибровозбудтелем, кг (m = 400 кг); aп – коэффициент приведения (aп=1,15 [1]).
mn = 1,15·400=460 кг.
Находим ωo:
,(2.12)
где Cр – приведенный коэффициент жёсткости рессорной подвески (принят Cр = 1·106 Н/м); Cб – приведенный коэффициент жёсткости балласта, Н/м.
Cб = Cуд ·Z ·a · l , (2.13)
где Z – заглубление под шпалу, м (Z=0,1 м); a – толщина клина, м (a=0,1 м); l – длина клина, м (l=1,35 м); Cуд – удельный коэффициент жёсткости балласта, Н/м4 , принимается по графику, при:
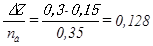(Cуд= 3·107 Н/м4 [1]).
Cб = 3·107 ·0,1·0,1·1,35 = 40,5 ·104 Н/м .
Тогда:
.
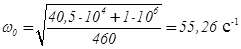Далее находится h:
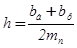, (2.14)
где bб , bр – соответственно коэффициент сопротивлений балласта и рессор, Н·с/м (принят bр = 5·103 Н·с/м [1]).
bб = bуд·Z ·a · l, (2.15)
где bуд – удельный коэффициент вязкостных сопротивлений, Н·с/м4, принимается по графику [1], при :
bуд = 12 · 104 Н·с/м4.
bб = 12·104·0,1·0,1·1,35 = 1,62·103 Н·с/м .
Тогда:
.
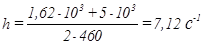В итоге по формуле (2.10) получили:
.
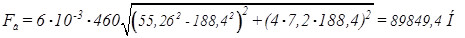Принята FВ = 90 кН.
По найденной FВ и принятой компоновке вибровозбудителя найдём вынуждающую силу одного дебаланса FВ’:
FВ’ = FВ / n,(2.16)
где n – принятое число дебалансов (n=4).
FВ’ = 90 / 4 = 22,5 кН .
Предварительно назначается расчётная длина вала дебаланса (рисунок 2.4) равная lв = 0,22.
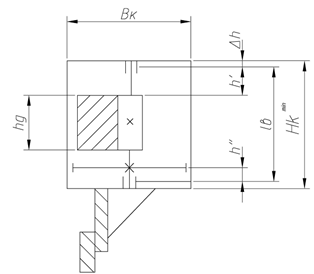
Рисунок 2.4 – Схема дебаланса
Для нахождения диаметра вала строится эпюра изгибающего момента. Для этого находятся реакции в точках опоры (рисунок 2.5)
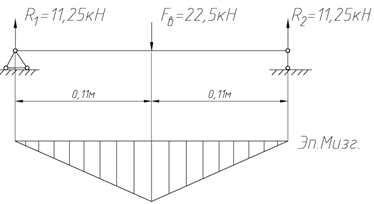
Рисунок 2.5 –Эпюра изгибающего момента
Максимальный изгибающий момент равен:
Mmax = R1 · 0,11 =11,25 · 0,11 =1,24 кН · м .
Прочность вала:
,(2.17)
где W – момент сопротивления при изгибе, м3 ; (для круглого сечения 
); [σ] – допускаемое напряжение, МПа .
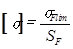,(2.18)
где σFlim – предел длительной выносливости, МПа; SF – коэффициент безопасности (для Ст 45 - SF = 1,75 , [2] стр. 90).
Для стали 45 :
σFlim =1,8 НВ,(2.19)
где НВ – твёрдость стали (для стали 45 HB = 248,5 , источник [2] стр.426).
Допускаемое напряжение равно:
[σ] = (1,8·248,5)/1,75 =255,6 МПа.
Находится диаметр вала по формуле:
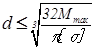;(2.20)
.
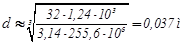Принят d = 40 мм ([2] стр. 296)
Компоновка дебалансов
Неуравновешенные части дебалансов в сечении имеют форму кругового сектора. Значение r0 (расстояние от оси вращения до центра тяжести дебаланса) зависит от угла сектора φ0 внешнего Rв и внутреннего rв радиусов дебаланса (рисунок 2.6).
Угол φ0 по рекомендациям [1] назначается 120˚. Радиус Rв предварительно определяется выражением:
Rв = 0,5· ВК – δД – bК, (2.21)
где δД – зазор между дебалансом и стенкой корпуса, м (δД = 0,045 м); bК – толщина корпуса виброплиты, м (bК = 0,01 м).
Rв = 0,5·0,35 – 0,02 – 0,01 = 0,12 м.
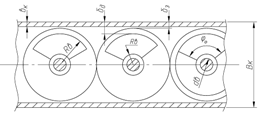
Рисунок 2.6 – Схема компоновки дебалансов
Расстояние от оси вращения до центра тяжести дебаланса:
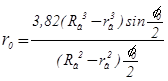.(2.22)
Внутренний радиус дебаланса:
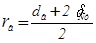,(2.23)
где δст – ширина ступицы, м (принимается конструктивно δст=0,02 м)
.
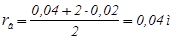Тогда
.
При требуемых силе Fв’ , частоте ω и установленном r0 определяется масса неуравновешенной части дебаланса:
;(2.24)
.
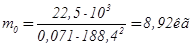Площадь дебаланса, м2 :
;(2.25)
.
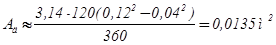Длина дебаланса, м:
,(2.26)
где ρ – плотность металла, кг/м3 (ρ =7800 кг/м3).
.
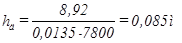Дата: 2019-05-28, просмотров: 187.
