Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Означення. Під кутом 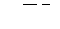 між двома векторами  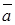і 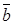 будемо розуміти кут, на який необхідно повернути вектор  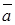 у додатньому напрямку (проти ходу годинної стрілки) до збігу з напрямком вектора  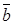 (див. рис. 4.1).

 

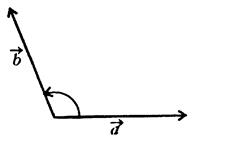
Рис. 4.1 До визначення кута між двома векторами

 

Нехай для визначеності, що 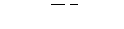. З означення і властивостей функції  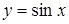випливає, що

 

.

 

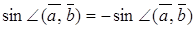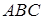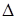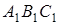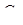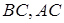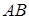Розглянемо два трикутники: (позначимо його через ) і , вершини  і  якого лежать на прямих  і  відповідно; позначимо трикутник  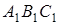через 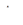. Зрозуміло, що вектори 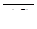і 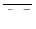  коллінеарні; також коллінеарні й вектори 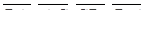. Введемо для коллінеарних векторів  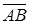і 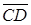 величину 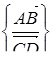, яка дорівнює відношенню довжин векторів  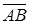і 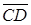, взятому зі знаком “+” , якщо вектори  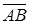і 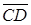  співнаправлені, і зі знаком “–“ у супротивному випадку.

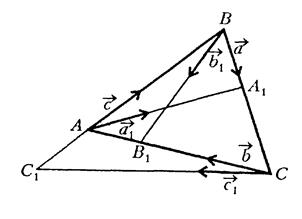
Рис. 4.2

 

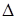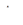Визначимо для трикутників  і  величину :

 

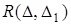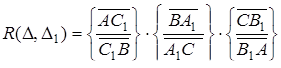                       (4.1)

 

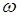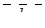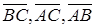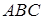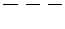Нехай далі  – трійка векторів , які коллінеарні векторам  (сторонам трикутника )  – трійка векторів , які коллінеарні векторам 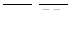і 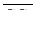. Визначимо для  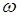і  величину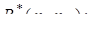

 

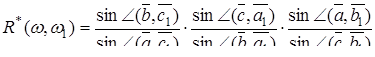              (4.2)

Лема. 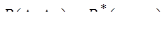                                         (4.3)

Доведення. Спочатку перевіримо, що 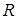 та 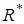 одного знака. Легко переконатися, що зміна напрямку одного з векторів 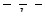,  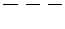не змінить величини 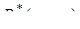, тому можна обрати напрямок кожного з них певним чином; наприклад, можна вважати вектори 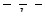,  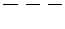такими, що збігаються за напрямком з векторами , 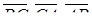, 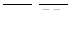і 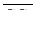 (див. рис. 4.2) .

У цьому випадку кожний з трьох дробів, що входять у вираз 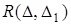 має той самий знак, що і відповідний дріб, який входить у вираз .

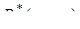Наприклад, дроби

 

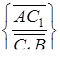 і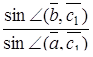

 

будуть додатними, якщо точка 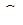 розташована між точками  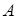і 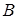, і від’ємними супротивному випадку (див. рис. 4.2, 4.3).

 

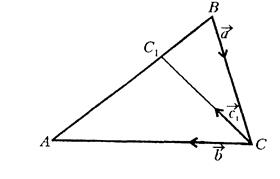
Рис. 4.3

 

Залишилось довести, що 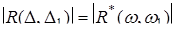. Маємо

 

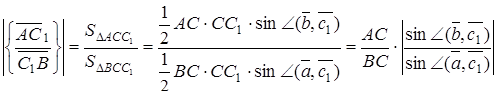
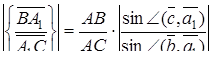
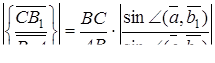
Перемножуючи ці три рівності, одержимо, що 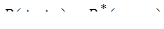. Лема доведена.

Далі буде необхідна рівність, що безпосередньо випливає з означення :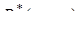

 

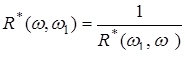.                                (4.4)

 

Сформулюємо тепер теореми Чеви та Менелая.

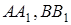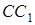Теорема Чеви. Для того, щоб прямі  і  перетиналися в одній точці, необхідно і достатньо, щоб виконувалась рівність

 

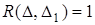                                              (4.5)

 

або еквівалентна рівність 

 

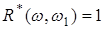                                   (4.5^/)

Теорема Менелая. Для того, щоб точки  лежали на одній прямій, необхідно і достатньо, щоб виконувалась рівність

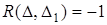                                       (4.6)

 

або еквівалентна рівність

 

                                    (4.6^/)

 

Доведення теореми Чеви.

Необхідність. Нехай прямі 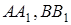,  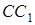перетинаються в одній точці. Доведемо, що виконуються умови (4.5) і (4.5^/).

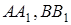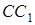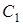Якщо прямі  і  перетинаються в одній точці, то або всі три точки  і  лежать на сторонах трикутника 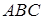, або одна з точок лежить на стороні трикутника, а дві інші – на продовженнях відповідних сторін.

У першому випадку всі дроби, що входять у вираз 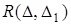, додатні, а в другому випадку один із трьох дробів, що входить у вираз 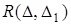, додатний, а два інші – від’ємні, так що знову вираз 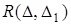(а отже, і  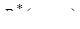– див. лему) більше нуля.

Доведемо, що 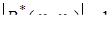 (оскільки >0, то з цього буде випливати, що  дорівнює одиниці).

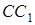Позначимо точку перетину прямих  і  через 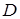(рис. 4.4а).

 

а)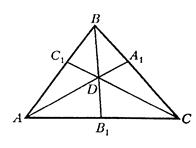

б)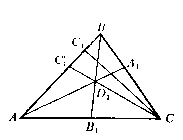

Рис. 4.4

 

Застосовуючи теорему синусів, одержимо

 

,

 

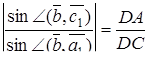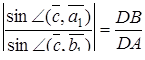
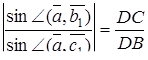
Перемножуючи ці рівності, знаходимо 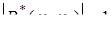, тим самим необхідність доведена.

Достатність. Доведення достатності проведемо методом від супротивного.

Припустимо, що 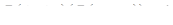, але прям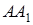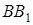і  ,  і 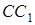 не проходять через одну крапку (див. рис. 4.4б).

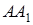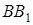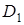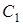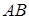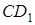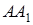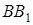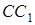Позначимо точку перетину прямих   і  через  , а через  – точку перетину прямих  і . Оскільки прямі  ,  і  перетинаються в одній точці, то

 

 

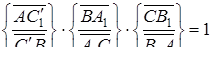
Але за умовою

 

,

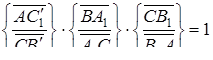звідки 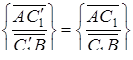. Так як і точка  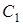і точка  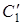 лежать на прямій 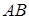, то з цього випливає, що точки  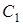та 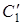 збігаються.

Теорема Чеви доведена.

 

Доведення теореми Менелая

Необхідність. Відомо, що точки  і 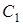 лежать на одній прямій. Необхідно довести рівності (4.6) та (4. ).

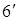Якщо точки  і 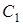 лежать на одній прямій, то або усі вони знаходяться на продовженнях  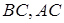і 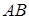 сторін трикутника 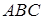, або ж дві з точок  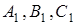знаходяться на відповідних ним сторонах, а третя – на продовженні.

В обох випадках вираження 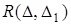 буде від’ємним. Доведемо тепер, що якщо точки  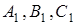– на одній прямій, то  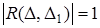(оскільки 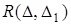<0, з цього буде випливати, що ).

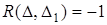Проведемо через точку 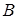 пряму, паралельну 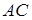, і позначимо точку її перетину з прямою  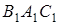через 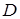 (див. рис. 4.5).

 

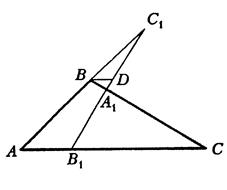
Рис. 4.5

 

Використовуючи подібність, одержимо

 

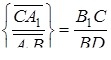
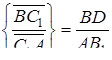
Додавши рівність 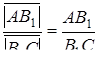 і перемноживши всі три рівності, одержимо, що 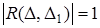. Необхідність умов теореми Менелая доведена.

Достатність. Доведення достатності умов (4.6) і (4. ) теореми Менелая проводиться аналогічно доведенню достатності умов (4.5) і (4. ) теореми Чеви.

Теорема доведена.

ВИСНОВКИ