Задача 1.1 У трикутнику 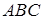 медіана
медіана 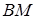 ділить відрізок
ділить відрізок 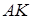 (точка
(точка 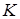 належить стороні
належить стороні 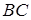 ) у відношенні 5:3 , починаючи від вершини
) у відношенні 5:3 , починаючи від вершини 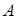 . У якому відношенні відрізок
. У якому відношенні відрізок 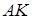 ділить медіану
ділить медіану 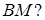
Розв’язок.
1-й спосіб
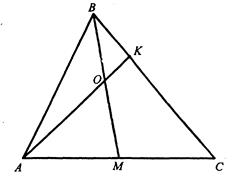 |
Нехай
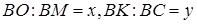
Введемо вектори 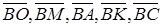 .
.
Розкладемо вектор 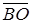 за неколінеарними векторами
за неколінеарними векторами 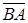 і
і 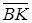 :
:
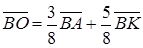
Оскільки 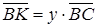 , то
, то
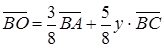 ,
,
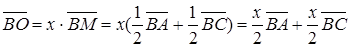 .
.
Виходячи з єдиності розкладу вектора 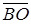 за неколінеарними векторами
за неколінеарними векторами 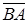 і
і 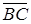 , маємо:
, маємо:
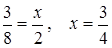 ,
, 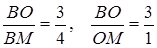
Відповідь 3 : 1.
2-й спосіб
Запишемо теорему Менелая для трикутника 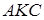 і прямої
і прямої 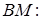
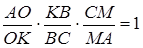
Виходячи з умови, маємо :
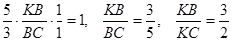
Запишемо теорему Менелая для трикутника 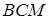 і прямої
і прямої 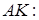
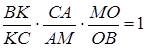
Тоді
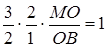
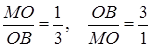
Відповідь: 3 : 1.
Задача 1.2 У трикутнику 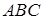 відрізок
відрізок 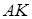 (
( 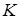 належить стороні
належить стороні 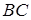 ) ділить медіану
) ділить медіану 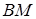 у відношенні 3:4, починаючи від вершини
у відношенні 3:4, починаючи від вершини 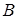 . У якому відношенні точка
. У якому відношенні точка 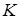 ділить сторону
ділить сторону 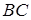
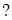
Розв’язок.
 |
1-й спосіб
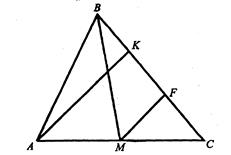
Проведемо 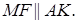
За умовою 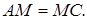 За теоремою Фалеса
За теоремою Фалеса 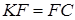 . Нехай
. Нехай 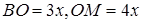 , тоді
, тоді
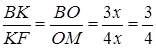
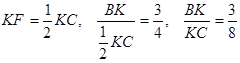
Відповідь: 3:8.
2-й спосіб
Запишемо теорему Менелая для трикутника 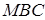 і прямої
і прямої 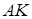 :
:
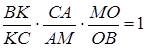
Тоді 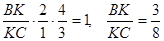 .
.
Відповідь: 3 : 8 .
Задача 1.3 Сторони трикутника 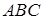 поділено точками
поділено точками 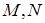 і
і 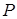 так, що
так, що
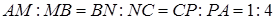 .
.
Знайти відношення площі трикутника, обмеженого прямими 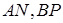 і
і 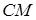 , до площі трикутника
, до площі трикутника 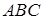 .
.
Розв’язок.
1-й спосіб
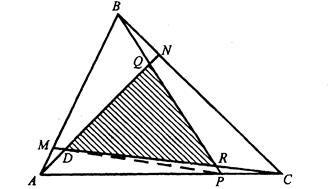 |
Нехай
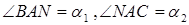 .
.
Використовуємо теорему синусів для трикутника 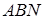 :
:
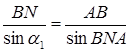 (1.3.1)
(1.3.1)
З трикутника 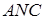 :
:
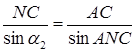 .
.
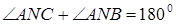 , тому
, тому 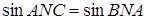
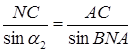 (1.3.2)
(1.3.2)
Поділимо почленно рівність (1.3.1) на рівність (1.3.2):
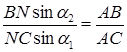
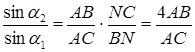
З 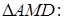
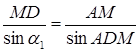 (1.3.3)
(1.3.3)
З 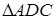 :
: 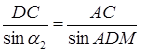 (1.3.4)
(1.3.4)
Поділимо почленно рівність (1.3.3) на рівність (1.3.4):
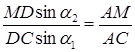 ,
, 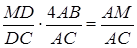
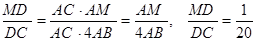 (*)
(*)
Нехай 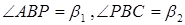 .
.
З 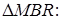
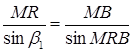 (1.3.5)
(1.3.5)
З 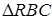 :
: 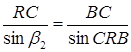 (1.3.6)
(1.3.6)
Поділимо почленно рівність (1.3.5) на рівність (1.3.6)
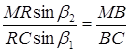
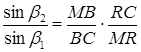
З 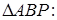
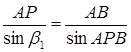 (1.3.7)
(1.3.7)
З 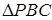 :
: 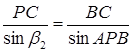 (1.3.8)
(1.3.8)
Поділимо почленно рівність (1.3.7) на рівність (1.3.8):
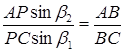 ,
, 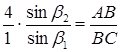
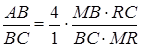 ,
, 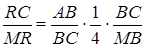
Оскільки 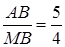 , то
, то
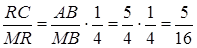
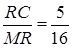 (**)
(**)
Використовуючи співвідношення (*) і (**), запишемо:
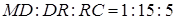 .
.
Аналогічно одержимо
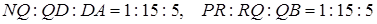 .
.
Використовуючи властивості площ, маємо:
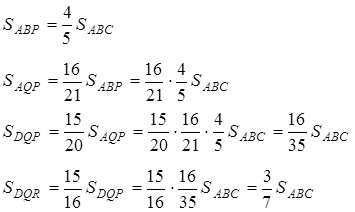
Відповідь: 3:7.
2-й спосіб
Запишемо теорему Менелая для трикутника 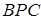 і прямої
і прямої 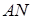 :
:
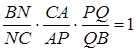
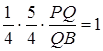
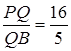 (1.3.9)
(1.3.9)
Запишемо теорему Менелая для трикутника 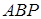 і прямої
і прямої 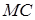 :
:
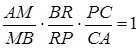
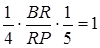
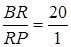 (1.3.10)
(1.3.10)
Використовуючи (1.3.9) і (1.3.10) дістанемо:
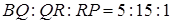
Аналогічно
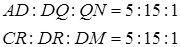
А далі розв’язуємо, як в 1-му способі.
Відповідь: 3 : 7.
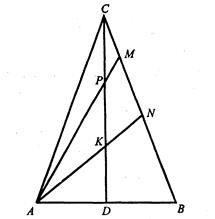
Задача 1.4 Висота 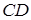 рівнобедреного трикутника
рівнобедреного трикутника 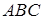 з основою
з основою 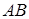 поділена на три рівні частини. Через точку
поділена на три рівні частини. Через точку 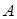 та точки поділу проведено прямі, які ділять бічну сторону, що дорівнює
та точки поділу проведено прямі, які ділять бічну сторону, що дорівнює 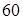 см, на три відрізки. Знайти ці відрізки.
см, на три відрізки. Знайти ці відрізки.
Розв’язок.
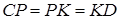
Запишемо теорему Менелая для трикутника 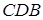 і прямої
і прямої 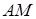 :
:
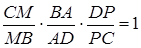 ,
,
 |
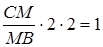 ,
, 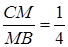
Звідси 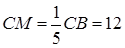 см ,
см , 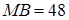 см.
см.
Запишемо теорему Менелая для трикутника 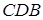 і прямої
і прямої 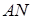 :
:
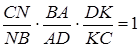
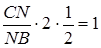 ,
, 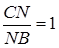
Звідси 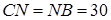 см,
см, 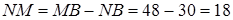 (см)
(см)
Відповідь: 12 см, 18 см, 30 см.
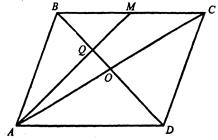
Задача 1.5 Через середину 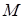 сторони
сторони 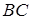 паралелограма
паралелограма 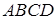 , площа якого дорівнює 1, і вершину
, площа якого дорівнює 1, і вершину 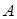 проведено пряму, яка перетинає діагональ
проведено пряму, яка перетинає діагональ 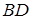 у точці
у точці 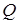 . Знайти площу чотирикутника
. Знайти площу чотирикутника 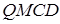 .
.
Розв’язок.
Запишемо теорему Менелая для трикутника  і прямої
і прямої 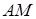 :
:
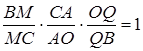 ,
,
 |
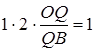 ,
, 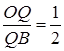
Оскільки площі трикутників з рівними висотами відносяться як основи, то
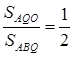
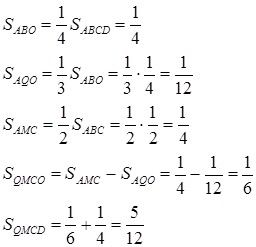
Відповідь: 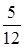
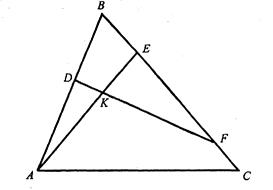
Задача 1.6. У трикутнику 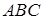 на стороні
на стороні 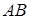 взято точку
взято точку 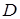 , а на стороні
, а на стороні 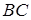 точки
точки 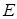 і
і 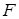 так , що
так , що 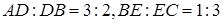 і
і 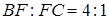 . У якому відношенні пряма
. У якому відношенні пряма 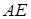 ділить відрізок
ділить відрізок 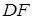 .
.
Розв’язок.
За умовою 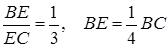 .
.
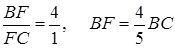 .
.
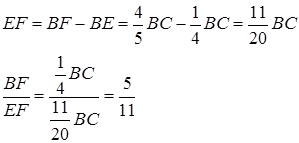
 |
Запишемо теорему Менелая для трикутника 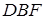 і прямої
і прямої 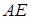 :
:
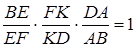 ,
,
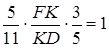 ,
,
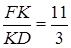 .
.
Відповідь: 11 : 3.
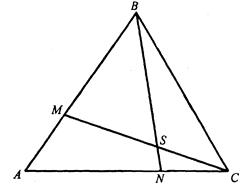
Задача 1.7 На сторонах 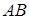 і
і 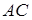 трикутника
трикутника 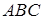 дано відповідно точки
дано відповідно точки 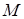 і
і 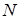 такі , що
такі , що 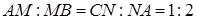 .У якому відношенні точка
.У якому відношенні точка 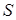 перетину відрізків
перетину відрізків 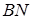 і
і 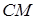 ділить кожен з цих відрізків ?
ділить кожен з цих відрізків ?
Розв’язок.
Запишемо теорему Менелая для трикутника 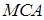 і прямої
і прямої  :
:
 |
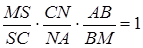 .
.
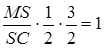 ,
, 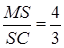
Запишемо теорему Менелая для трикутника 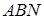 і прямої
і прямої 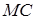 :
:
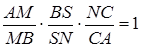 ,
,
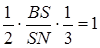 ,
, 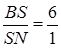
Відповідь: 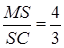 ,
, 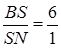 .
.
Задача 1.8 Ортоцентр 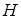 трикутника
трикутника 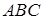 (ортоцентр – точка перетину висот) ділить висоту навпіл. Довести , що
(ортоцентр – точка перетину висот) ділить висоту навпіл. Довести , що 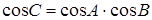 , де
, де 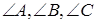 – кути трикутника.
– кути трикутника.
Доведення.
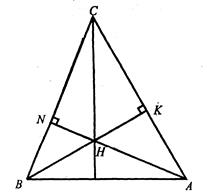 |
Нехай
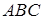 - даний трикутник,
- даний трикутник, 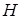 - його ортоцентр,
- його ортоцентр, 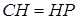 .
.
Запишемо теорему Менелая для трикутника 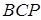 і прямої
і прямої 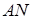 :
:
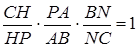
Виходячи з умови 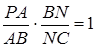 .
.
З 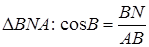 .
.
З 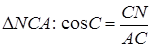 .
.
З 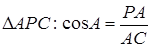 .
.
Підставимо знайдені залежності в теорему Менелая:
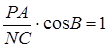 ,
,
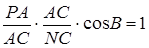 ,
,
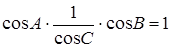
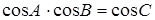 ,
,
що і треба було довести.
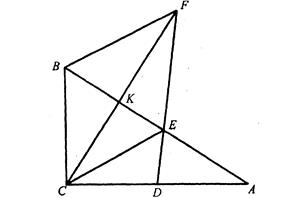
Задача 1.9 З вершини 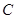 прямого кута трикутника
прямого кута трикутника 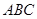 проведено висоту
проведено висоту 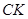 , а в трикутнику
, а в трикутнику 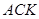 проведено бісектрису
проведено бісектрису  . Пряма, що проходить через точку
. Пряма, що проходить через точку 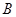 паралельно
паралельно  , перетинає
, перетинає 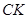 у точці
у точці 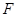 . Довести, що пряма
. Довести, що пряма 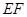 ділить відрізок
ділить відрізок 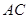 навпіл.
навпіл.
 |
Розв’язок.
Нехай 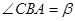 , тоді
, тоді 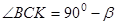 ,
, 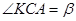 .
.
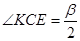 (
(  - бісектриса).
- бісектриса).
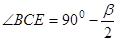
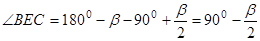 .
.
Тому 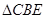 - рівнобедрений,
- рівнобедрений, 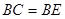 .
.
Запишемо теорему Менелая для трикутника 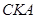 і прямої
і прямої 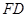 :
:
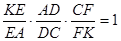
Трикутники 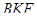 і
і 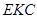 подібні,
подібні,
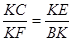 .
.
Тоді
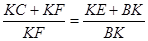
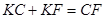
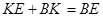
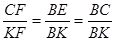 (1.9.1)
(1.9.1)
З подібності трикутників 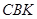 і
і 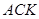 запишемо:
запишемо:
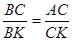 (1.9.2)
(1.9.2)
З трикутника 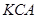 за властивістю бісектриси:
за властивістю бісектриси:
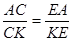 (1.9.3)
(1.9.3)
Порівнюючи співвідношення (1.9.1), (1.9.2), (1.9.3) маємо:
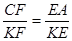
Підставимо знайдений результат у теорему Менелая :
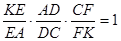 ,
, 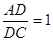
Тобто 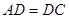 , що і треба було довести.
, що і треба було довести.
Задачі для самостійної роботи
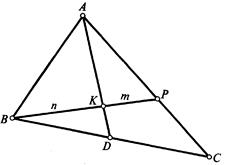
Задача 1.10 Нехай 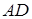 – медіана трикутника
– медіана трикутника 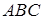 . На
. На 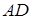 взята точка
взята точка 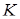 так, що
так, що 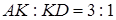 . В якому співвідношенні пряма
. В якому співвідношенні пряма 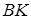 ділить площу трикутника
ділить площу трикутника  ?
?
 |
Розв’язок.
Відношення площ трикутників 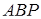 та
та 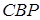 дорівнює відношенню відрізків
дорівнює відношенню відрізків 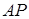 та
та 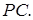 Застосовуючи теорему Менелая до трикутника ACD та прямої BP, маємо
Застосовуючи теорему Менелая до трикутника ACD та прямої BP, маємо
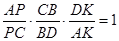 ,
,
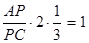 ,
, 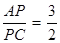 .
.
Відповідь: AP:PC=3:2.
Задача 1.11 Три кола різних радіусів розташовані на площині так, що жодне з них не лежить повністю в колі, яке обмежено іншим колом. Кожній парі кіл поставимо у відповідність точку перетину зовнішніх подвійних дотичних. Довести, що одержані три точки лежать на одній прямій.
Доведення.
Нехай радіуси кіл з центрами 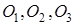 рівні
рівні 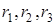 відповідно . Тоді
відповідно . Тоді
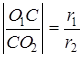 ,
,
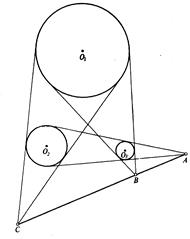 |
так як кіла з центрами
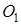 и
и 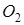 гомотетичні відповідно точки С, а відношення радіусів
гомотетичні відповідно точки С, а відношення радіусів 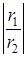 - коефіцієнт гомотетіі.
- коефіцієнт гомотетіі.
Аналогічно 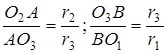 .
.
Таким чином , 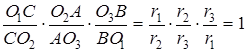 .
.
З теореми оберненої до теореми Менелая маємо, що точки А,В,С лежать на одній прямій.
Задача 1.12 В 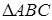 бісектриса
бісектриса 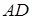 поділяє
поділяє 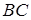 в відношенні 2:1. В якому відношенні медіана
в відношенні 2:1. В якому відношенні медіана 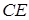 поділяє цю бісектрису ?
поділяє цю бісектрису ?
Розв’язок .
Застосовуємо теорему Менелая до трикутника 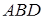 та прямої
та прямої 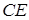
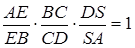 .
.
Так як 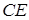 – медіана, то
– медіана, то 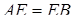 , звідси
, звідси
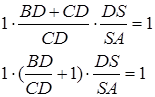
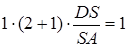
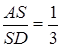
Відповідь: 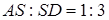 .
.
Задача 1.13 В правильном трикутнику 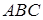 зі стороною
зі стороною 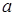 точка
точка 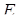 –середина
–середина 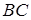 ,
, 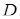 – середина
– середина 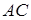 ,
, 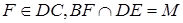 ,
, 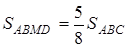 . Знайти
. Знайти 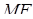 .
.
 |
Розв’язок.
Площа правильного трикутника дорівнює 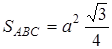 .
.
Розглянемо трапецію 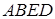
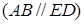 ,
, 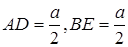 . Знайдемо висоту
. Знайдемо висоту 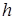 цієї трапеції:
цієї трапеції:
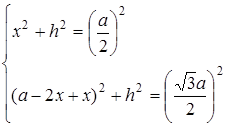
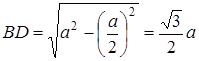
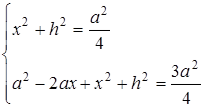

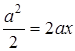
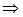
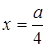
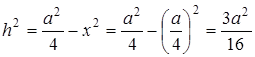
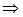
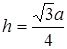
Оскільки 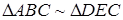 , то
, то 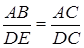 , звідки
, звідки 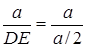
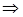
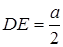 .
.
За умовою 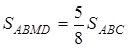 , де
, де 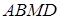 – трапеція з висотою
– трапеція з висотою 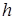 , тоді
, тоді
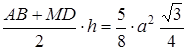
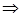
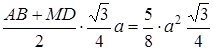
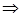
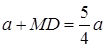
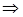
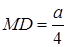
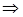
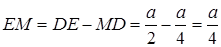 .
.
Застосовуємо теорему Менелая до трикутника 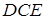 та прямої
та прямої 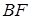 :
:
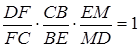
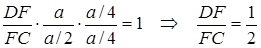 .
.
Застосовуємо теорему Менелая до трикутника  та прямої
та прямої 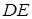 :
:
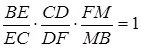
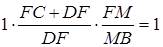
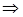
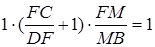
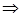
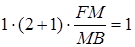
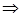
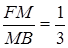 .
.
Оскільки 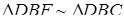 , то
, то 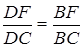 , звідки
, звідки 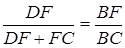
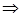
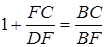
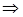
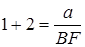
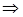
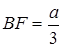 .
.
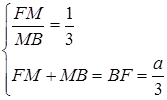
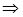
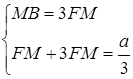
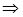
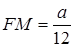 .
.
Відповідь: 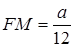
Задача 1.14 Дан паралелограм 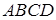 . Точка
. Точка 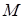 поділяє відрізок
поділяє відрізок 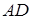 в відношені
в відношені 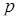 , а точка
, а точка 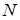 поділяє відрізок
поділяє відрізок 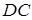 в відношенні
в відношенні 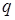 . Прямі
. Прямі 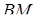 та
та 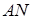 перетинаються в точці
перетинаються в точці 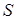 . Обчислити відношення
. Обчислити відношення 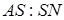 .
.
Розв’язок.
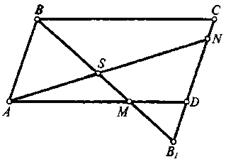
Застосуємо теорему Менелая до трикутника 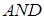 та прямої
та прямої 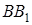 :
:
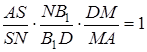
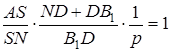
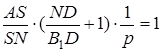 (*)
(*)
Оскільки 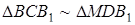 , то
, то
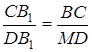
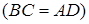
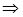
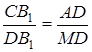
Так як 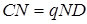
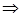
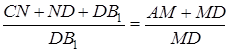
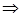
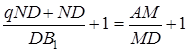

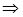
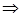
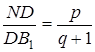 .
.
Підставляємо 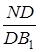 в (*):
в (*): 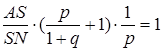
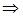
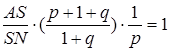 .
.
Відповідь: 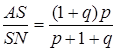 .
.
Задача 1.15 Коло 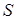 дотикається кола
дотикається кола 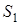 та кола
та кола 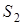 в точках
в точках 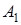 і
і 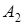 . Довести, що пряма
. Довести, що пряма 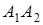 проходить через точку перетину загальних зовнішніх або загальних внутрішніх дотичних до кіл
проходить через точку перетину загальних зовнішніх або загальних внутрішніх дотичних до кіл 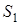 та
та 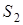 .
.
Доведення.
Нехай 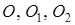 – центри кіл
– центри кіл 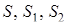 ;
; 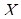 - точка перетину прямих
- точка перетину прямих 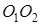 і
і 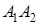 . Застосовуючи теорему Менелая до трикутника
. Застосовуючи теорему Менелая до трикутника 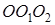 і точок
і точок 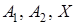 , знаходимо
, знаходимо 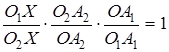 ,
,
отже, 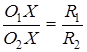 ,
,
де 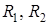 – радіуси кіл
– радіуси кіл 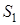 і
і 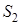 відповідно. Отже,
відповідно. Отже, 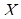 – точка перетину загальних зовнішніх або загальних внутрішніх дотичних до кіл
– точка перетину загальних зовнішніх або загальних внутрішніх дотичних до кіл 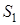 і
і 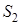 .
.
Задача 1.16 а) Серединний перпендикуляр до бісектриси 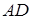 трикутника
трикутника 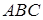 перетинає пряму
перетинає пряму 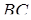 в точці
в точці 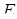 . Довести, що
. Довести, що 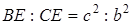 .
.
б) Довести, що точки перетину серединних перпендикулярів до бісектрис трикутників і продовжень відповідних сторін лежать на одній прямій.
Доведення.
а) Нехай для визначеності 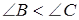 .
.
Тоді 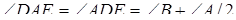 , звідки
, звідки 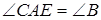 .
.
Так як 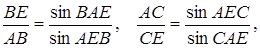 то
то
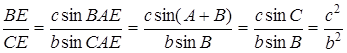 .
.
б) В задачі а) точка 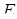 лежить на продовженні сторони
лежить на продовженні сторони 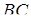 , так як
, так як
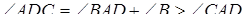 .
.
Тому, використовуючи результат задачі а) і теорему Менелая, одержуємо необхідне.
Задача 1. 1 7 На сторонах 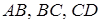 чотирикутника
чотирикутника 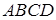 (або на їхніх продовженнях) взяті точки
(або на їхніх продовженнях) взяті точки 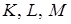 . Прямі
. Прямі 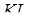 і
і 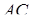 перетинаються в точці
перетинаються в точці 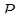 , прямі
, прямі 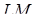 і
і 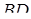 - в точці
- в точці 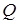 . Довести, що точка перетину прямих
. Довести, що точка перетину прямих 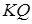 і
і 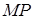 лежить на прямій
лежить на прямій 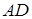 .
.
Доведення.
Нехай 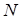 - точка перетинання прямих
- точка перетинання прямих 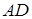 і
і 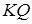 ,
, 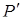 - точка перетинання прямих
- точка перетинання прямих 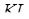 і
і 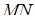 . Застосовуючи теорем Дезарга до трикутників
. Застосовуючи теорем Дезарга до трикутників 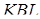 і
і 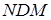 , одержуємо, що точки
, одержуємо, що точки 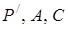 лежать на одній прямій. Виходить,
лежать на одній прямій. Виходить, 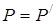 .
.
Задача 1.18 Задан чотирикутник 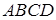 . Продовження його сторін
. Продовження його сторін 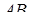 та
та 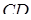 перетинаються в точці
перетинаються в точці 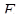 , продовження сторін
, продовження сторін 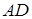 та
та 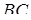 перетинаються в точці
перетинаються в точці 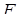 . Довести, що середини відрізків
. Довести, що середини відрізків 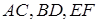 лежать на одній прямій.
лежать на одній прямій.
Доведення.
Нехай 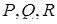 – середини відрізків
– середини відрізків 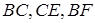 , а точки
, а точки 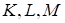 – середини
– середини 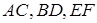 . Точка
. Точка 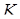 лежить на прямій
лежить на прямій 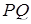 , точка
, точка 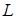 – на прямій
– на прямій 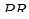 , точка
, точка 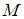 – на прямій
– на прямій 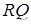 . Достатньо довести, що
. Достатньо довести, що
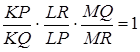 .
.
Але
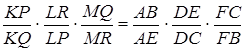 ,
,
а останній добуток дорівнює 1 згідно з теоремою Менелая для трикутника 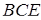 та прямої
та прямої 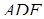 .
.
Задача 1.19 Пряма Сімсона. Нехай 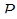 – точка кола, описаного навколо трикутника
– точка кола, описаного навколо трикутника 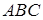 , а точки
, а точки 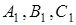 – основи перпендикулярів, опущених з точки
– основи перпендикулярів, опущених з точки 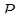 на прямі
на прямі 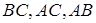 . Довести, що точки
. Довести, що точки 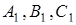 лежать на одній прямій.
лежать на одній прямій.
Доведення.
Нехай 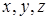 – відстані від точки
– відстані від точки 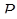 , яка взята на дузі
, яка взята на дузі 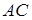 описаного кола, до вершин
описаного кола, до вершин 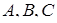 відповідно, а
відповідно, а 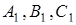 – проекції точки
– проекції точки 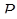 на прямі
на прямі 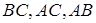 . Нехай також
. Нехай також 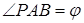 ,
, 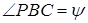 ,
, 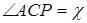 . Тоді орієнтовані відрізки з точністю до знаку такі:
. Тоді орієнтовані відрізки з точністю до знаку такі:
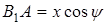 ,
, 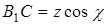 ,
, 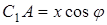 ,
, 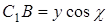 ,
,
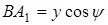 ,
, 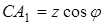 .
.
Записуючи їх відношення, приписуючи ним потрібні знаки, та перемножуючи, одержимо рівність
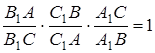 .
.
Звідси й випливає, що точки 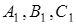 лежать на одній прямій.
лежать на одній прямій.
Задача 1.20 На сторонах 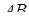 та
та 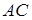 трикутника
трикутника 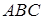 взято точки
взято точки 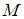 та
та 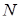 такі, що
такі, що 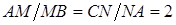 . Відрізки
. Відрізки 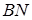 та
та 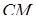 перетинаються в точці
перетинаються в точці 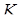 . Знайти відношення відрізків
. Знайти відношення відрізків 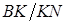 .
.
Розв’язок.
Застосуємо теорему Менелая до трикутника 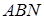 та січної
та січної 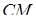 . Одержимо
. Одержимо
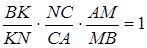 ,
,
оскільки 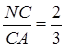 , а
, а 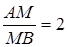 , то
, то 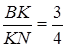 .
.
Відповідь: 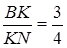 .
.
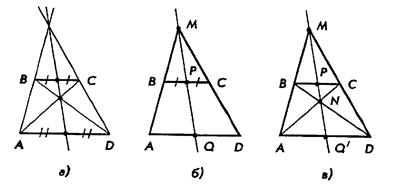
Задача 1. 21 Довести, що пряма, яка проходить через середини основ трапеції, проходить через точку перетину її діагоналей та точку перетину прямих, які містять бокові сторони (див. рис. а).
Доведення.
1 спосіб.
Нехай 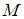 - точка перетину прямих, що містять бокові сторони
- точка перетину прямих, що містять бокові сторони 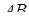 і
і 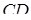 трапеції
трапеції 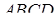 ,
, 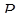 - середина основи
- середина основи 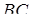 ,
, 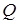 – точка перетину прямої
– точка перетину прямої 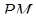 з основою
з основою 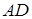 (див. рис. б). Доведемо, що
(див. рис. б). Доведемо, що 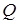 – середина відрізку
– середина відрізку 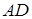 , тобто точка
, тобто точка 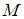 лежить на прямій, яка проходить через середини основ трапеції.
лежить на прямій, яка проходить через середини основ трапеції.
Оскільки трикутник 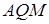 подібний до трикутника
подібний до трикутника 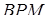 за першою ознакою подібності трикутників (
за першою ознакою подібності трикутників ( 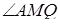 – спільний,
– спільний, 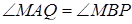 ), то відношення
), то відношення
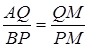 . Аналогічно, трикутник
. Аналогічно, трикутник 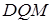 подібний до трикутника
подібний до трикутника  , тому
, тому 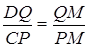 . З цих рівностей одержуємо, що
. З цих рівностей одержуємо, що 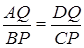 . Так як
. Так як 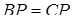 , то
, то 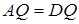 , тобто
, тобто 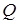 – середина основи
– середина основи 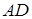 .
.
Позначимо через 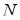 точку перетину діагоналей
точку перетину діагоналей 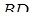 і
і 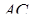 , а через
, а через 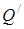 – точку перетину прямих
– точку перетину прямих 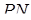 і
і 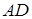 (див. рис. в). Аналогічно до попереднього, використовуючи подібність: трикутник
(див. рис. в). Аналогічно до попереднього, використовуючи подібність: трикутник 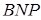 подібний до трикутника
подібний до трикутника 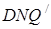 і трикутник
і трикутник 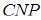 подібний до трикутника
подібний до трикутника 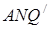 , доводиться, що
, доводиться, що 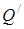 – середина основи
– середина основи 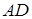 . Тобто точка
. Тобто точка 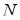 лежить на прямій, що проходить через середини основ трапеції.
лежить на прямій, що проходить через середини основ трапеції.
2 спосіб.
Нехай 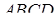 задана трапеція з основами
задана трапеція з основами 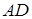 і
і 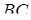 . Застосуємо теорему Менелая до трикутника
. Застосуємо теорему Менелая до трикутника 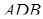 і трьом точкам
і трьом точкам 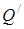 (середина основи
(середина основи 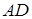 ),
), 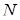 (точка перетину діагоналей
(точка перетину діагоналей 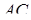 і
і 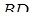 ),
), 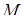 (точка перетину прямих
(точка перетину прямих 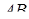 і
і 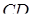 ) (див. рис. в).
) (див. рис. в).
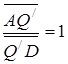 ,
, 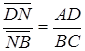 ,
, 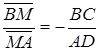 ,
,
так як трикутник 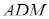 подібний до трикутника
подібний до трикутника 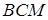 . Звідси випливає, що
. Звідси випливає, що
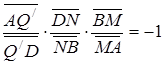 ,
,
тому точки 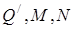 лежать на одній прямій. Аналогічно доводиться, що середина
лежать на одній прямій. Аналогічно доводиться, що середина 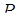 відрізка
відрізка 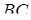 лежить на прямій
лежить на прямій 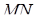 .
.
Задача 1.22 Через точку 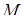 перетину діагоналей чотирикутника проведена січна. Відрізок цієї січної, що замкнений між однією парою протилежних сторін чотирикутника, поділяється точкою
перетину діагоналей чотирикутника проведена січна. Відрізок цієї січної, що замкнений між однією парою протилежних сторін чотирикутника, поділяється точкою 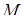 навпіл. Довести, що відрізок січної, що замкнений між продовженнями іншої пари протилежних сторін чотирикутника поділяється точкою
навпіл. Довести, що відрізок січної, що замкнений між продовженнями іншої пари протилежних сторін чотирикутника поділяється точкою 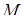 також навпіл.
також навпіл.
Доведення.
Нехай січна 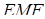 зустрічає сторони
зустрічає сторони 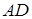 і
і 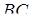 чотирикутника
чотирикутника 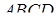 в точках
в точках 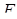 і
і 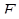 , а продовження сторін
, а продовження сторін 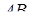 і
і 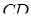 – в точках
– в точках 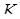 і
і 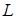 . Тоді скориставшись теоремою Менелая для трикутників
. Тоді скориставшись теоремою Менелая для трикутників 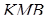 і
і 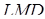 , які перетинаються прямими
, які перетинаються прямими  і
і 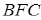 , одержуємо, що
, одержуємо, що
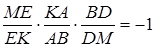 і
і 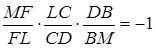 .
.
Тоді
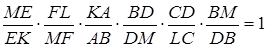 .
.
Але за умовою 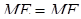 , і для чотирикутника
, і для чотирикутника 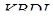 і січної
і січної 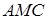 згідно з теоремою Менелая маємо
згідно з теоремою Менелая маємо
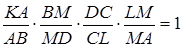 .
.
Отже, 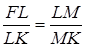 або
або 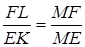 . Звідси
. Звідси 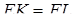 і
і 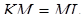 .
.
РОЗДІЛ 2
Дата: 2019-05-28, просмотров: 325.