В одній точці перетинаються
1) медіани трикутника;
2) висоти трикутника;
3) бісектриси трикутника;
4) відрізки, що з’єднують вершини трикутника з точками дотику вписаного кола (точка Жергонна);
5) відрізки, що з’єднують вершини трикутника з точками дотику відповідних вневписаних кіл (точка Нагеля);
(Вневписане коло трикутника – це коло, що дотикається однієї сторони трикутника та продовженн двох інших його сторін. Для кожного трикутника існує точно три вневписаних кола. Центром вневписаного кола, яке дотикається сторони АВ , є точка перетину бісектрис зовнішніх кутів А та В.)
6) відрізки, що з’єднують вершини трикутника з вершинами правильних трикутників, побудованих на його протилежних сторонах у зовнішню сторону (точка Торричеллі).
Доведення.
1) Оскільки 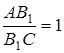 ,
, 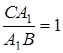 ,
, 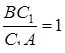 , то
, то 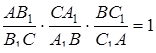 , отже медіани трикутника перетинаються в одній точці.
, отже медіани трикутника перетинаються в одній точці.
2) Розглянемо випадок, коли трикутник  гострокутний.
гострокутний.
Маємо 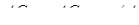 ,
, 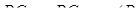 ,
, 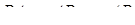 ,
, 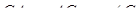 ,
, 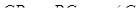 ,
, 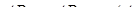 .
.
Звідси випливає
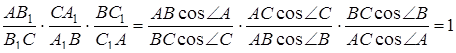
Якщо трикутник  тупокутний, то дві висоти цього трикутника не є чевіанами. У випадку, коли точно один з відрізків
тупокутний, то дві висоти цього трикутника не є чевіанами. У випадку, коли точно один з відрізків 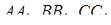 є чевіаною, а інші з’єднують вершини з точками продовжень протилежних сторін, при цьому ці відрізки не паралельні, твердження теореми Чеви також виконується. Залишається повторити проведені вище обчислення для тупокутного трикутника.
є чевіаною, а інші з’єднують вершини з точками продовжень протилежних сторін, при цьому ці відрізки не паралельні, твердження теореми Чеви також виконується. Залишається повторити проведені вище обчислення для тупокутного трикутника.
3) З властивості бісектрис випливають наступні рівності:
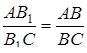 ,
, 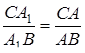 ,
, 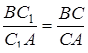 .
.
Перемножуючи відповідно ліві та праві частини цих рівностей, одержуємо умову теореми Чеви.
4) З властивостей дотичних, проведених з однієї точки до кола маємо:
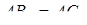 ,
, 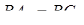 ,
, 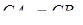 .
.
Звідси випливає рівність з теореми Чеви: 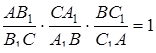 .
.
5)
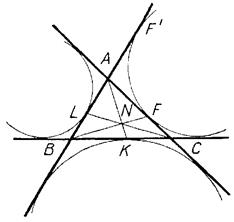
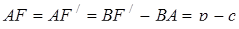 , де
, де 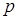 - півпериметр трикутника
- півпериметр трикутника 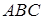 ,
,
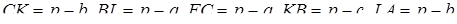 ,
,
Отже, 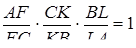 .
.
Це і означає, що прямі 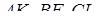 перетинаються в одній точці.
перетинаються в одній точці.
6) Нехай 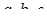 – сторони трикутника
– сторони трикутника 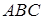 . Нехай
. Нехай 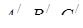 – вершини правильних трикутників, побудованих на сторонах
– вершини правильних трикутників, побудованих на сторонах 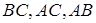 відповідно, а
відповідно, а 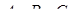 – точки перетину відрізків
– точки перетину відрізків 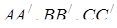 з відповідними сторонами або їх продовженнями. Зазначимо, що
з відповідними сторонами або їх продовженнями. Зазначимо, що
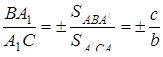 ,
,
при цьому знак “мінус” береться в тому випадку, коли точка 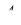 лежить зовні відрізка
лежить зовні відрізка 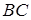 . Аналогічно розписуються відношення для точок
. Аналогічно розписуються відношення для точок 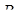 та
та 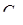 . Після перемноження маємо
. Після перемноження маємо 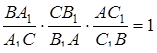 . Наслідки доведено.
. Наслідки доведено.
Іноді теорему Чеви зручно використовувати, вводячи замість відношень відрізків відношення синусів деяких кутів.
Теорема Чеви в формі синусів. Нехай на сторонах 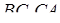 і
і 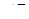 трикутника
трикутника 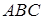 взяті точки
взяті точки 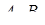 ,
, 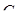 . Прямі
. Прямі 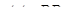 і
і 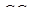 проходять через одну точку або паралельні тоді і тільки тоді, коли
проходять через одну точку або паралельні тоді і тільки тоді, коли
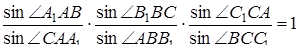 . (3.3)
. (3.3)
Доведення.
Ми повинні переписати “в синусах” теорему Чеви. Запишемо її у формі (3.2):
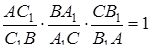 .
.
Доведемо цю теорему для випадку, коли точки  і
і  лежать на сторонах трикутника. Випадки іншого розташування точок вимагають несуттєвих змін міркувань.
лежать на сторонах трикутника. Випадки іншого розташування точок вимагають несуттєвих змін міркувань.
Нехай  .
.
Інші позначення зрозумілі з рисунка 3.3.
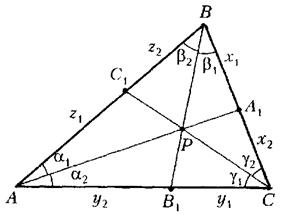
Рис. 3.3 До доведення теорими Чеви у формі синусів
Застосовуючи теорему синусів до трикутників 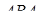 і
і 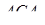 , маємо
, маємо
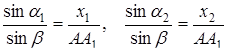
Або
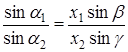
Аналогічно, застосовуючи теорему синусів до трикутників 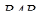 і
і 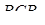 , маємо
, маємо
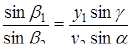 ,
,
і до трикутників 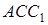 і
і 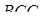 :
:
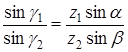 .
.
Перемножуючи записані співвідношення, знаходимо
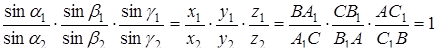
Отже, умова нашої теореми рівносильна умові звичайної теореми Чеви.
Теорема доведена.
При доведенні теореми ми не застосовували відношень орієнтованих відрізків. В загальному випадку необхідно розглянути не тільки орієнтовані відрізки, але й орієнтовані кути, припускаючи, наприклад, що 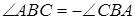 і т.п.
і т.п.
Далі наведемо мало відому стереометричну теорему Чеви для довільного тетраедра.
Т еорема Чеви для тетраедра. Нехай 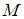 – точка всередині тетраедра
– точка всередині тетраедра 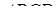 ,
, 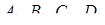 – точки перетину площин
– точки перетину площин 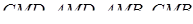 з ребрами
з ребрами 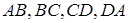 відповідно (див. рис. 3.4). Тоді
відповідно (див. рис. 3.4). Тоді
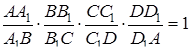 (3.4)
(3.4)
І навпаки, якщо для точок 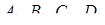 , що лежать на відповідних ребрах, виконується співвідношення (3.4), то площини
, що лежать на відповідних ребрах, виконується співвідношення (3.4), то площини 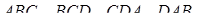 проходять через одну точку.
проходять через одну точку.
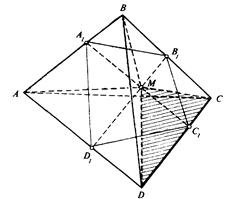
Рис. 3.4 До формуліровки теореми Чеви для тетраедра
Доведення необхідності легко одержати, якщо помітити, що точки 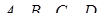 (див. рис. 3.4) лежать в одній площині (це площина, що проходить через прямі
(див. рис. 3.4) лежать в одній площині (це площина, що проходить через прямі 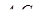 та
та 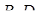 , які перетинаються в точці
, які перетинаються в точці 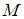 ), і застосувати теорему Менелая.
), і застосувати теорему Менелая.
Обернена теорема доводиться так само, як і обернена теорема Менелая в просторі: необхідно провести площину через точки 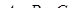 і довести, що ця площина перетне ребро
і довести, що ця площина перетне ребро 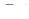 в точці
в точці 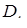 .
.
Дата: 2019-05-28, просмотров: 347.