Досить ефективно при розв’язанні деяких задач застосовується мало відома стереометрична теорема Менелая для довільного тетраедра.
Теорема Менелая для тетраедра. У довільному тетраедрі 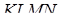 точки
точки 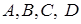 належать ребрам
належать ребрам 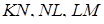 і
і 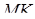 відповідно (див. рис. 2.1). Для того, щоб точки
відповідно (див. рис. 2.1). Для того, щоб точки 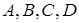 належали однієї площині, необхідно і достатньо, щоб виконувалось співвідношення
належали однієї площині, необхідно і достатньо, щоб виконувалось співвідношення
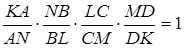 (2.1)
(2.1)
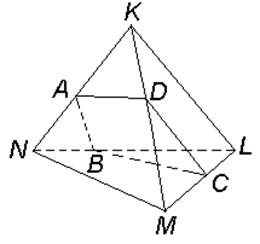
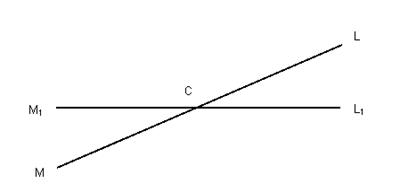
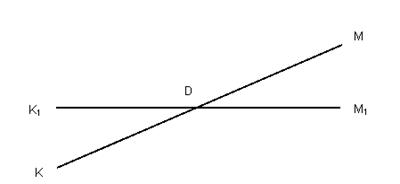
Рис 2.1 До формулювання теореми Менелая для довільного тетраедра
Доведення. Необхідність. Нехай чотирикутник 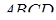 – перетин даного тетраедра деякою площиною
– перетин даного тетраедра деякою площиною  . Проведемо
. Проведемо 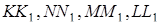 – перпендикуляри до площи-ни
– перпендикуляри до площи-ни  . Розглянемо «фрагмент» – перетин ребра
. Розглянемо «фрагмент» – перетин ребра 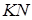 площиною
площиною  (див. рис. 2.2).
(див. рис. 2.2).
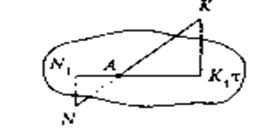
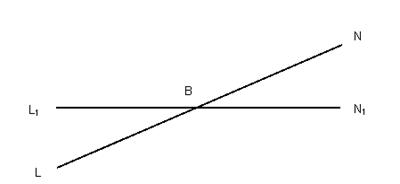
Рис 2.2 До доведення теореми Менелая
Трикутники 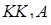 та
та 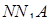 подібні, тому
подібні, тому 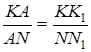 .
.
Трикутники 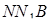 та
та 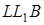 подібні, тому
подібні, тому 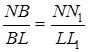 .
.
Трикутники 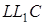 та
та 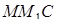 подібні, тому
подібні, тому 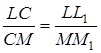 .
.
Трикутники 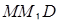 та
та 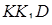 подібні, тому
подібні, тому 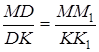 .
.
Перемножуючи знайдені пропорції, приходимо до рівності:
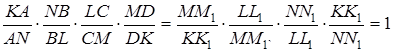 .
.
Достатність. Припустимо, що виконується співвідношення (2.1), але точки 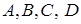 не лежать в одній площині. Проведемо через точки
не лежать в одній площині. Проведемо через точки 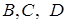 площину
площину 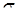 , що перетинає ребро
, що перетинає ребро 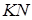 в деякій точці
в деякій точці 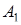 , відмінної від
, відмінної від 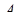 . Тому
. Тому 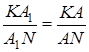 ,
,
отже, співвідношення (2.1) для точок 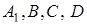 виконуватися не буде. Оскільки ми прийшли до протиріччя з вихідною умовою (не виконується рівність (2.1)), то наше припущення невірне й площина
виконуватися не буде. Оскільки ми прийшли до протиріччя з вихідною умовою (не виконується рівність (2.1)), то наше припущення невірне й площина 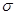 пройде через точку
пройде через точку 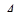 .
.
Теорема доведена.
Наведемо застосування цієї теореми до розв’язання стереометричних задач.
Задача 2.1 У тетраедрі 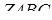 точки
точки 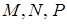 належать ребрам
належать ребрам 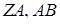 і
і 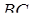 відповідно (див. рис. 2.3), причому
відповідно (див. рис. 2.3), причому 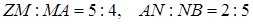 і
і 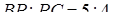 . Через точки
. Через точки 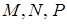 проведена площина
проведена площина  . У якому відношенні ця площина поділяє об’єм тетраедра?
. У якому відношенні ця площина поділяє об’єм тетраедра?
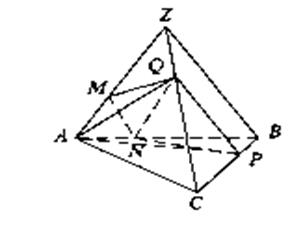
Рис. 2.3 До задачі 2.1
Розв’язок. Нехай площина 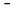 перетинає ребро
перетинає ребро 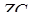 в точці
в точці 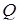 . Чотирикутник
. Чотирикутник 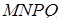 – переріз даного тетраедра площиною
– переріз даного тетраедра площиною 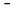 . Визначимо, у якому відношенні точка
. Визначимо, у якому відношенні точка 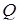 поділяє ребро
поділяє ребро 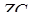 . На підставі співвідношення (2.1) та умови задачі маємо
. На підставі співвідношення (2.1) та умови задачі маємо
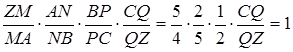 ,
,
звідки 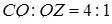 .
.
У багатограннику 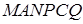 проведемо переріз через ребро
проведемо переріз через ребро 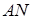 і вершину
і вершину 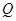 . Цей переріз розбиває розглянутий багатогранник на трикутну піраміду
. Цей переріз розбиває розглянутий багатогранник на трикутну піраміду 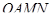 і чотирикутну піраміду
і чотирикутну піраміду 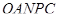 , яка діагональним перерізом
, яка діагональним перерізом 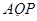 розбивається на дві трикутні піраміди:
розбивається на дві трикутні піраміди: 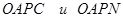 .
.
Нехай 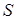 – площа грані
– площа грані 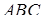 ,
, 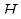 – довжина висоти тетраедра, проведена з вершини
– довжина висоти тетраедра, проведена з вершини 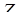 ,
, 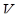 – об’єм даного тетраедра. Визначимо об’єми трьох отриманих вище трикутних пірамід. Для піраміди
– об’єм даного тетраедра. Визначимо об’єми трьох отриманих вище трикутних пірамід. Для піраміди 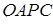 :
:
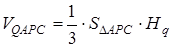
де 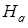 – довжина висоти трикутної піраміди
– довжина висоти трикутної піраміди 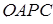 , проведена з вершини
, проведена з вершини 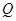 на площину грані
на площину грані 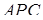 (
( 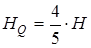 ). Тоді
). Тоді
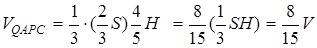
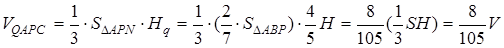
Нехай далі 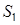 – площа грані
– площа грані 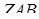 ,
, 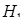 – довжина висоти даного тетраедра, проведена з вершини
– довжина висоти даного тетраедра, проведена з вершини 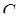 на площину грані
на площину грані 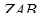 . Тоді
. Тоді
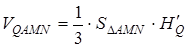
де 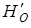 – довжина перпендикуляра, проведеного з вершини
– довжина перпендикуляра, проведеного з вершини 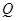 на площину грані
на площину грані 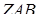 (
( 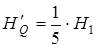 ) і
) і
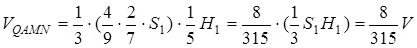
Знайдемо тепер об’єм багатогранника 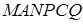 :
:
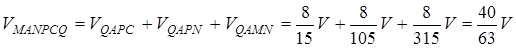
Отже, 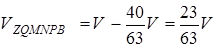 .
.
У такий спосіб шукане відношення дорівнює 23:40.
Відповідь: 23:40.
Задача 2.2. Об’єм тетраедра 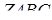 дорівнює 5. Через середини ребер
дорівнює 5. Через середини ребер 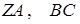 проведена площина, яка перетинає ребро
проведена площина, яка перетинає ребро 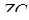 в точці
в точці 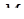 . При цьому відношення довжини відрізка
. При цьому відношення довжини відрізка 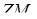 до довжини відрізка
до довжини відрізка 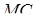 дорівнює
дорівнює 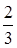 . Знайдіть площу перерізу тетраедра зазначеною площиною, якщо відстань до неї від вершини
. Знайдіть площу перерізу тетраедра зазначеною площиною, якщо відстань до неї від вершини 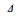 дорівнює 1.
дорівнює 1.
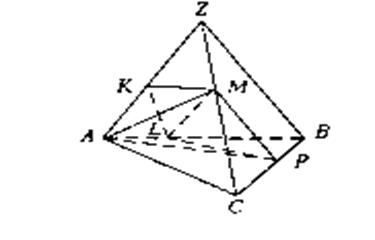
Рис. 2.4 До задачі 2.2
Розв’язок.
Нехай 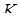 і
і 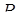 – середини ребер
– середини ребер 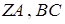 відповідно і
відповідно і 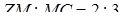 .
.
Чотирикутник 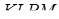 – заданий за умовою переріз. На підставі теореми Менелая
– заданий за умовою переріз. На підставі теореми Менелая
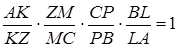 ,
,
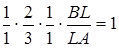 ,
,
звідки 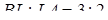 .
.
З'єднаємо точки 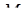 і
і 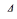 ,
, 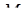 і
і 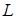 ,
, 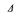 і
і 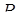 .
.
Нехай 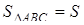 і довжина висоти тетраедра, проведена з вершини
і довжина висоти тетраедра, проведена з вершини 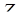 На рисунку не наведено), дорівнює
На рисунку не наведено), дорівнює 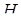 . Згідно з умовою задачі
. Згідно з умовою задачі 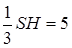 . Висота піраміди
. Висота піраміди 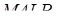 , проведена з вершини
, проведена з вершини 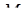 дорівнює
дорівнює 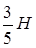 .
.
Знайдемо тепер об’єм піраміди 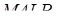 :
:
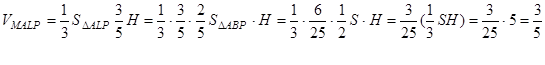
Далі нехай 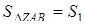 і довжина висоти тетраедра, проведена з вершини
і довжина висоти тетраедра, проведена з вершини 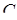 на грань
на грань 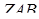 дорівнює
дорівнює 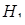 . Тоді об’єм піраміди
. Тоді об’єм піраміди 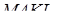 дорівнює
дорівнює
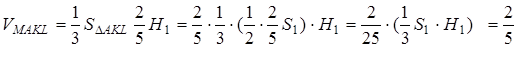
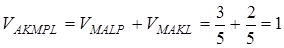 .
.
З іншої сторони (враховуючи, що відстань від вершини 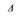 до площини перерізу за умовою задачі дорівнює 1), маємо
до площини перерізу за умовою задачі дорівнює 1), маємо
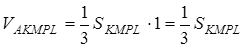
Отже, 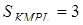 .
.
Відповідь: 3.
Задача 2.3 В піраміді 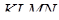 проведений переріз
проведений переріз 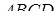 так, що точка
так, що точка 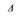 лежить на ребрі
лежить на ребрі 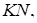 точка
точка 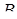 – на ребрі
– на ребрі 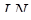 , точка
, точка 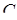 – на ребрі
– на ребрі 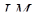 , точка
, точка 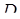 – на ребрі
– на ребрі 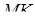 . Відомо, що
. Відомо, що 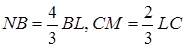 ,
, 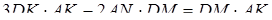 .
.
Знайти відношення об’ємів частин, на які площина 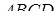 поділяє піраміду.
поділяє піраміду.
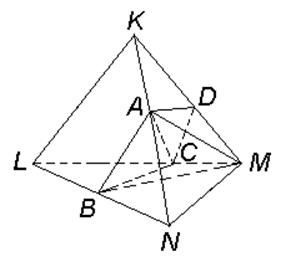
Рис 2.5 До задачі 2.3
Розв’язок.
З умови задачі безпосередньо випливає, що
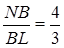 (2.3.1)
(2.3.1)
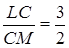 (2.3.2)
(2.3.2)
Нехай 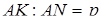 ,
, 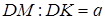 .
.
Згідно з теоремою Менелая маємо
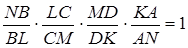
Враховуючи (2.3.1) і (2.3.2) й прийняті вище позначення одержуємо
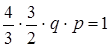 ,
,
звідки 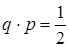 (2.3.3)
(2.3.3)
Розділивши обидві частини останньої рівності з умови задачі на 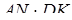 , одержуємо
, одержуємо
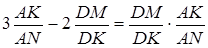
або
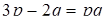 (2.3.4)
(2.3.4)
З (2.3.3) і (2.3.4) складаємо систему
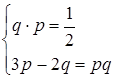
Розв’язуємо цю систему:
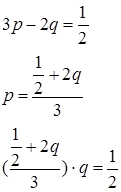
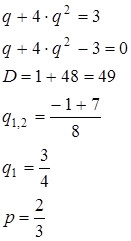
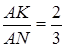 і
і 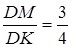
Розбиваємо багатогранник 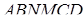 на три трикутні піраміди:
на три трикутні піраміди: 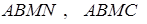 ,
, 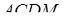 .
.
Нехай 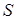 – площа трикутника
– площа трикутника 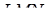 ,
, 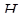 – довжина висоти даної піраміди, проведена з вершини
– довжина висоти даної піраміди, проведена з вершини 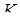 ,
, 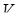 – об’єм даної піраміди,
– об’єм даної піраміди, 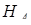 – довжина висоти піраміди
– довжина висоти піраміди 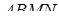 , проведена з вершини
, проведена з вершини 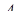 . Тоді маємо
. Тоді маємо
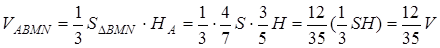
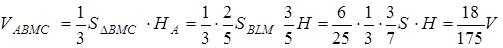
Нехай 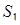 – площа грані
– площа грані 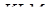 ,
, 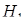 – довжина висоти даної піраміди, проведена з вершини
– довжина висоти даної піраміди, проведена з вершини 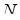 на площину грані
на площину грані 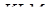 ,
, 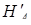 – довжина перпендикуляра, опущеного з точки
– довжина перпендикуляра, опущеного з точки 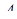 на площину грані
на площину грані 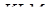 . Тоді маємо
. Тоді маємо
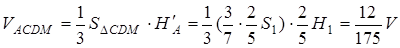
Знайдемо об’єм багатогранника 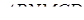 :
:
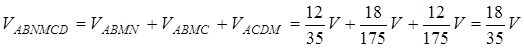
Отже, 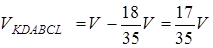 .
.
Таким чином, шукане відношення дорівнює 17:18.
Відповідь: 17:18.
Задача 2.4 Задана піраміда 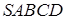 , основа якої має форму опуклого чотирикутни-ка
, основа якої має форму опуклого чотирикутни-ка 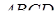 зі взаємно перпендикулярними діагоналями
зі взаємно перпендикулярними діагоналями 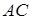 і
і 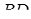 . Основа перпендикуляра, опущеного з вершини
. Основа перпендикуляра, опущеного з вершини 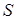 на основу піраміди, збігається з точкою
на основу піраміди, збігається з точкою 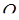 – перетином діагоналей
– перетином діагоналей 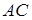 і
і 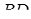 . Довести, що основи перпендикулярів, опущених із точки
. Довести, що основи перпендикулярів, опущених із точки 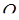 на бічні грані піраміди, лежать на одному колі.
на бічні грані піраміди, лежать на одному колі.
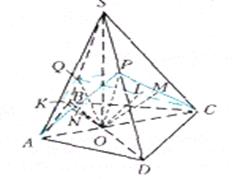
Рис. 2.6 До задачі 2.4
Розв’язок.
Нехай 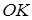 – перпендикуляр до площини
– перпендикуляр до площини 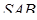 ,
, 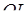 – перпендикуляр до площини
– перпендикуляр до площини  ,
, 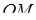 – перпендикуляр до площини
– перпендикуляр до площини 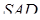 . Покажемо, наприклад, що точка
. Покажемо, наприклад, що точка 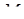 – ортоцентр грані
– ортоцентр грані 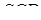 . В площині грані
. В площині грані 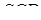 проведемо промінь
проведемо промінь 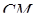 до перетину з ребром
до перетину з ребром 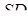 в точці
в точці 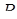 . Згідно з умовою,
. Згідно з умовою, 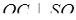 і
і 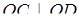 . Тому
. Тому 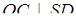 .
.
Згідно з теоремою про три перпендикуляри ( 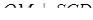 ,
, 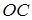 – похила,
– похила, 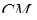 –її проекція на
–її проекція на 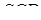 ) маємо, що
) маємо, що 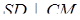 . Аналогічно доводиться, що
. Аналогічно доводиться, що 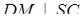 . Отже, точка
. Отже, точка 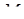 – ортоцентр грані
– ортоцентр грані 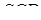 .
.
Аналогічно доводиться, що точки 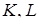 і
і 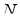 також є ортоцентрами відповідних граней.
також є ортоцентрами відповідних граней.
З'єднаємо точки 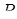 і
і 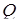 . Згідно з теоремою про три перпендикуляри
. Згідно з теоремою про три перпендикуляри 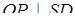 . З'єднаємо точки
. З'єднаємо точки 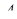 і
і 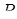 . Згідно з теоремою про три перпендикуляри
. Згідно з теоремою про три перпендикуляри 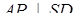 .
.
Оскільки з точки 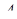 в грані
в грані 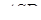 на
на 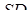 можна провести тільки один перпендикуляр, то відрізок
можна провести тільки один перпендикуляр, то відрізок 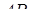 пройде через точку
пройде через точку 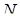 . Отже, висоти, проведені в гранях
. Отже, висоти, проведені в гранях 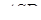 і
і 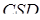 з вершин
з вершин 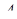 і
і 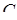 на ребро
на ребро 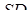 , проходять через точки
, проходять через точки 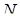 і
і 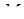 відповідно і перетинають ребро
відповідно і перетинають ребро 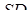 в точці
в точці 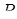 .
.
Аналогічно доводиться, що висоти граней 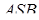 і
і 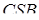 , проведені з вершин
, проведені з вершин 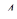 і
і 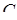 на ребро
на ребро 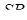 , проходять через точки
, проходять через точки 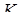 і
і 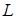 відповідно і попадають в ту саму точку
відповідно і попадають в ту саму точку 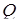 на ребрі
на ребрі 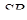 .
.
Розглянемо трикутник 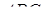 , у якому
, у якому 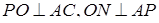 і
і 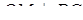 (див. рис 2.7)
(див. рис 2.7)
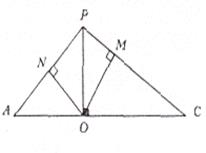
Рис 2.7
Нехай 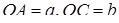 і
і 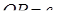 . Тоді
. Тоді 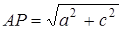 і
і 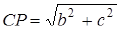 .
.
З 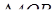 :
:
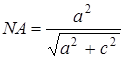 ;
; 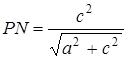 ;
; 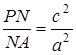 .
.
З 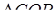 :
:
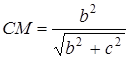 ;
; 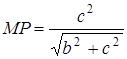 ;
; 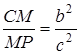 .
.
Аналогічно розглянемо 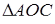 , нехай
, нехай 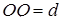 (див. рис. 2.8).
(див. рис. 2.8).
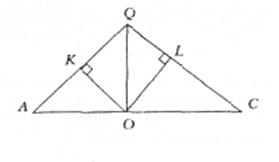
Рис 2.8
З 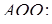
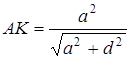 ;
; 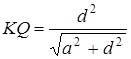 ;
; 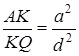
З 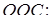
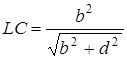 ;
; 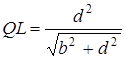 ;
; 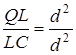
Точки 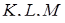 і
і 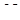 належать відповідно ребрам
належать відповідно ребрам 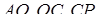 і
і 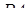 тетраедра
тетраедра 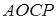 . Розглянемо добуток
. Розглянемо добуток
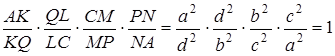
З того, що розглянутий добуток дорівнює 1, випливає, що точки 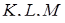 і
і 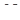 належать однієї площини (назвемо неї
належать однієї площини (назвемо неї 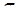 ). Побудуємо на
). Побудуємо на 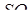 , як на діаметрі сферу (на рисунку не наведено). Оскільки
, як на діаметрі сферу (на рисунку не наведено). Оскільки 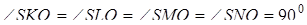 , то вершини цих кутів лежать на побудованій сфері. А так як точки
, то вершини цих кутів лежать на побудованій сфері. А так як точки 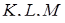 і
і 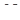 належать також площині
належать також площині 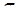 , то ці точки лежать на перетині площини
, то ці точки лежать на перетині площини 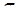 зі сферою тобто на колі.
зі сферою тобто на колі.
Задачі для самостійної роботи
Задача 2.5 В тетраедрі 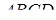 через середини
через середини  та
та 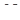 ребер
ребер 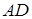 та
та 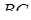 проведена площина, яка перетинає ребра
проведена площина, яка перетинає ребра 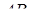 та
та 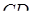 відповідно в точках
відповідно в точках 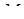 та
та 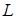 . Площа чотирикутника
. Площа чотирикутника 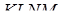 дорівнює 16, а відношення довжини відрізка
дорівнює 16, а відношення довжини відрізка 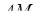 до довжини відрізка
до довжини відрізка 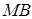 дорівнює 0,5. Обчислити відстань від вершини
дорівнює 0,5. Обчислити відстань від вершини 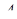 до площини
до площини 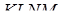 , якщо об’єм багатогранника
, якщо об’єм багатогранника  дорівнює 8.
дорівнює 8.
Розв’язок.
Дата: 2019-05-28, просмотров: 366.