1.1 Орієнтовані відрізки
Нехай на прямій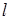 
задані відрізки 
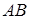та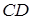 
. Розглянемо вектори 
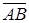та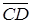 
(див. рис. 1). Зі шкільного курсу геометрії відомо, що існує таке число 
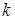, що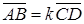 
. Якщо 
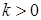, то вектори називають однаково спрямованими, а якщо 
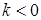, то говорять , що вектори протилежно спрямовані (див. рис. 1.1а та 1.1б відповідно).
а) б)
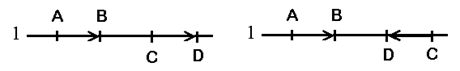
Рис. 1.1
При цьому відрізки 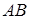та 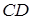ми будемо називати однаково спрямованими, якщо 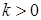і протилежно спрямованими, якщо 
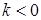. Саме число 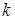будемо називати відношенням орієнтованих відрізків 
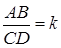(при 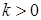це відношення є просто відношенням довжин відрізків, а при 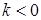– відношенням довжин, взяте зі знаком мінус).
В подальшому всі відношення виду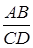 
будемо розуміти як відношення орієнтованих відрізків.
Якщо відрізки 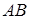і лежать не на одній прямій, а на паралельних прямих, то також можна говорити про однаково і протилежно орієнтовані відрізки і їхні відношення (див. рис. 1.2).
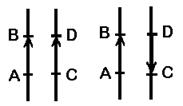
Рис. 1.2
 |
Наприклад, нехай
і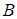 
– точки площини, а 
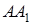і 
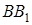– перпендикуляри, опущені з цих точок на деяку пряму 
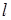(див. рис. 1.3).
Рис. 1.3
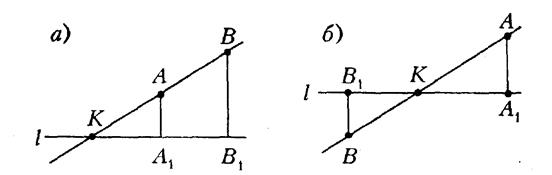
Тоді, якщо точки 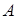і 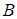лежать по одну сторону від прямої 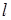, то відрізк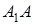и 
й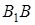 
орієнтовані однаково (див. рис. 1.3а), а якщо по різні сторони – протилежно (див. рис. 1.3б), при цьому в обох випадках 
.
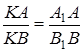Зазначемо такі важливі властивості відношень:
1) 
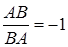2) 
.
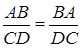Нехай тепер на прямій 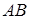задана ще третя точка – 
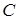. На рисунку 1.4 показано, якими можуть бути відношення 
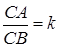в залежності від положення точки 
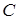на прямій 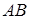. Так, якщо 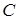лежить на відрізку 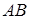, то 
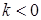; якщо точка 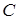лежить ліворуч від точки 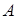, то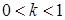 
; якщо точка 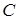лежить праворуч від точки 
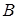, то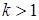 
.
Отже, задаючи відношення орієнтованих відрізків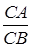 
ми однозначно визначаємо положення точки 
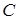на прямій .
 |
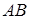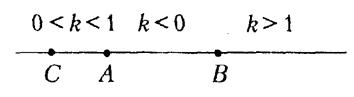Рис. 1.4
Зауваження. Точки 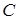, для якої 
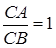, не має на прямій 
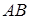(можна приєднати до прямої нескінчено удалену точку 
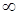і вважати, що саме для неї 
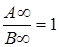). Слід зазначити, що просте відношення довжин відрізків 
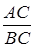неоднозначно задає точку 
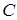на прямій 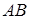– таких точок, як правило, дві (за виключенням середини відрізка 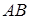, для якої 
).
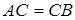Теорема Менелая
Теорема Менелая дійшла до нас в арабському перекладі книги «Сферика» грецького математика та астронома Менелая Олександрійського (І-ІІ століття нашої ери). Теорема Менелая дозволяє в деяких випадках знаходити відношення відрізків, а також доводити належність трьох точок одній прямій.
Теорема Менелая. Нехай задано трикутник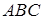 
і три точки 
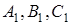на прямих 
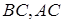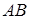і відповідно. Точки 
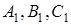лежать на одній прямій тоді і тільки тоді, коли
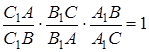(1.1)
Зауваження. Іноді добуток відношень в теоремі Менелая записують так:
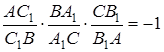
Тут всі відношення, що перемножуються – це відношення орієнтованих відрізків .
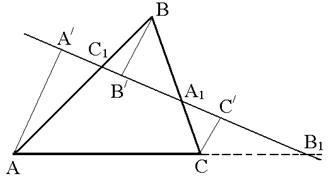
Рис. 1.5
Доведення.
Необхідність. Нехай пряма 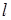перетинає прямі 
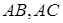та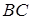 
в точках 
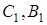і 
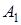відповідно (див. рис. 1.5) і 
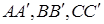– перпендикуляри, які опущено з точок 
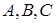на пряму 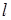. Як було доведено раніше,
.
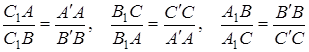Перемножаючи записані відношення, маємо
.
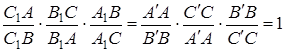Достатність. Проведемо пряму 
. Ми повинні довести, що ця пряма перетинає 
в точці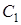 
. Насамперед доведемо, що 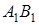дійсно перетинає 
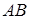. Припустимо, що 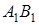паралельна 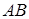(див. рис. 1.6). Але тоді
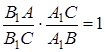
Звідси та з рівності (1.1) випливає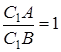 
, що неможливо.
Нехай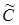 
– точка перетину прямих 
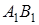та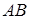 
. По вже доведеному
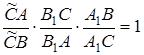
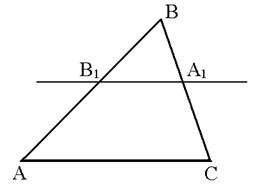
Рис. 1.6
Порівнюючи з умовою, одержуємо, що
.
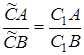Оскільки мова йде про відношення орієнтованих відрізків, то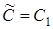 
, що потрібно було довести довести. Отже, теорема Менелая повністю доведена.
Зауваження 1. При розв’язанні конкретних обчислювальних задач, якщо відомо, що точки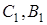 
і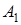 
лежать на одній прямій, можна не турбуватися про запис відношень орієнтованих відрізків в формулі (1.1), а обмежитися відношеннями їх довжин.
Зауваження 2. Якщо замінити в (1.1) орієнтовані відношення відношеннями довжин, обернена теорема перестає бути вірною, тобто точки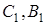 
і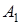 
, для яких виконується (1.1), не повинні лежати на одній прямій.
Наприклад, нехай точки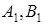 
взяті на сторонах 
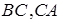трикутника 
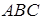так, що 
, 
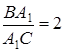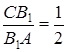і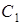 
– середина сторони 
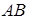, тоді
,
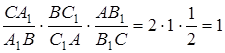але точки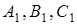 
не лежать на одній прямій.
Дата: 2019-05-28, просмотров: 285.
