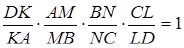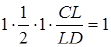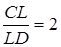Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

 

,

 

, .

 

Знайдемо об’єм :

 

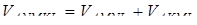
Знаходимо 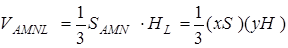, де 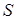 - площа ,  - висота 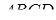 проведена з вершини ,  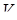- об’єм .

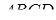Знаходимо висоту :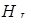        

 

        

   

 

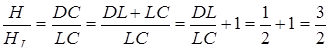
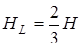
Знаходимо площу .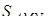

 

,

,  

 

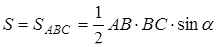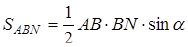
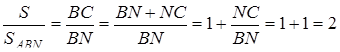
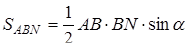Тоді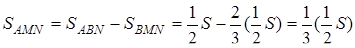          

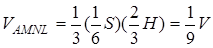
Знайдемо об’єм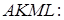

 

 ,

 

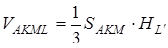де 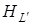 - висота, проведена з вершини  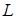до ,  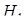- висота проведена з вершини  до .

Знаходимо висоту :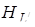

 

 

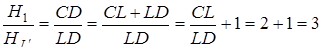
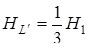
Знаходимо площу .

 

,       

 

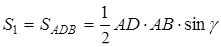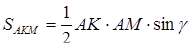
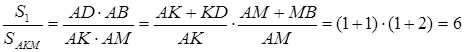
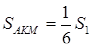
Тоді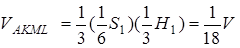              

Отже,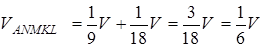   

Тоді     

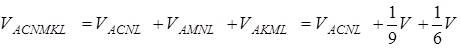
Залишилось знайти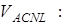

 

,

 

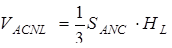де .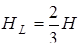

 

Знайдемо площу .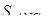

 

,

 

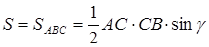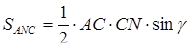
Тоді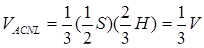     

Отже

 

 

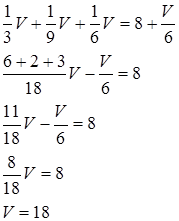
Знаходимо відстань від вершини  до площини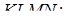

 

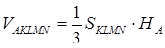
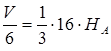
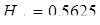
Відповідь: .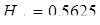

 

Задача 2.6 В тетраедрі 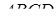 проведено переріз  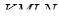так, що точка  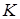лежить на ребрі 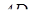, точка  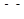– на ребрі 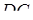, точка  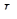– на ребрі 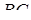, точка  - на ребрі . Переріз 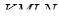 ділить піраміду на дві частини. Знайти відношення об’ємів цих частин, якщо відомі наступні співвідношення між довжинами відрізків 

 

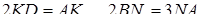 та .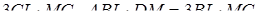

 

Розв’язок.

Нам треба знайти .

Нехай 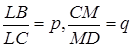, відомо .

 

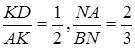Згідно з теоремою Менелая для тетраедра

 

,

, .

 

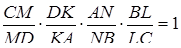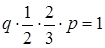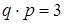З умови задачі маємо

 

 

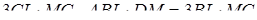
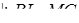
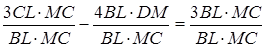
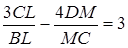
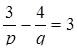
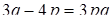
Складаємо систему :

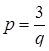
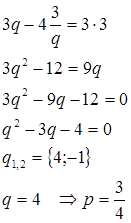
Отже, .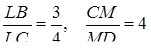

 

Розбиваємо багатогранник  на три трикутні піраміди:

.

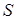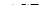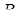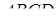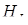Знайдемо об’єм піраміди . Нехай  – площа трикутника ,  – довжина висоти даної піраміди, проведена з вершини ,  – об’єм піраміди ,  –довжина висоти піраміди .

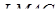Тоді 

 

 

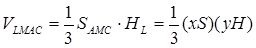
Знайдемо  та .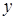

 

,

 

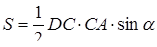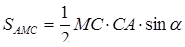
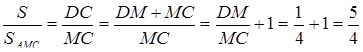
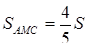
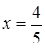
Знайдемо висоту

 

:

  

 

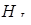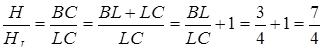
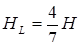
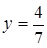
Отже,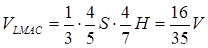                      

 

Знайдемо об’єм піраміди :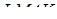

 

 

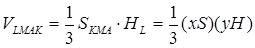
Відомо, що 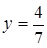. Знайдемо .

 

,  

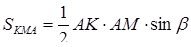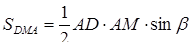
Відомо, що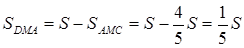

 

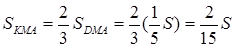
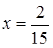
Отже,

 

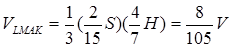
Знайдемо об’єм піраміди . Нехай 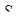 - площа грані ,  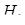– довжина висоти даної піраміди проведена з вершини  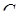 на площину грані ,  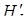–довжина перпендикуляра, опущеного з точки  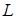на площину грані .

Тоді

 

 

Знайдемо 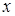 та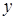   

,    

  

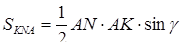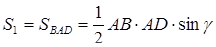
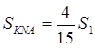
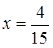
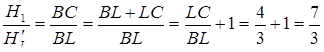
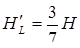
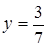
Отже,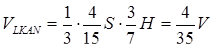             

 

Об’єм багатогранника

 

.

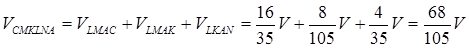Отже, .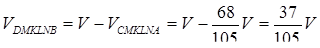

Остаточно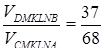

 

Відповідь: 37:68.

 

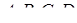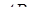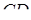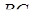Задача 2.7 Точки   не належать одній площині. Відрізки   і  поділені точками та   так, що , а відрізки  і 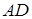 поділені точками  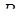та 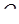 так, що 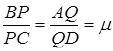. Довести, що точки  та 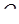 належать одній площині.

 

Доведення.

Розглянемо добуток 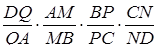. Підставляємо відомі відношення з умови

 

 

Це і є необхідна й достатня умова належності точок  та 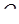 одній площині.

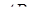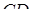Задача 2.8 Площина, яка проходить через середини  та  ребер  та  тетраедра 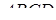, перетинає ребро  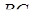в точці 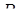, а ребро  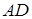 – в точці 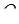. Довести, що .

 

Доведення.

За умовою задачі 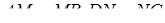. Згідно з теоремою Менелая для тетраедра

 

, .

 

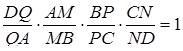
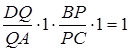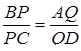Задача 2.9 Сфера дотикається сторін 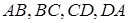 просторового чотирикутника в точках  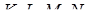відповідно. Довести, що точки  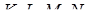лежать в одній площині.

Доведення.

З рівності відрізків дотичних випливає, що

 

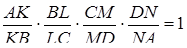
Проведемо площину через точки 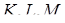. Нехай вона перетинає  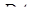в точці 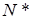. Тоді

 

.

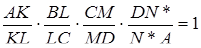Знаходимо, що , але тоді 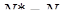. Отже, точки  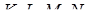лежать в одній площині.

РОЗДІЛ 3

ТЕОРЕМ И ЧЕВИ ДЛЯ ТРИКУТНИКА ТА ТЕТРАЕДРА.

ТЕОРЕМА ЧЕВИ В ФОРМІ СИНУСІВ