Міністерство освіти і науки України
Дніпропетровський національний університет
Механіко-математичний факультет
Кафедра математичного аналізу
ДИПЛОМНА РОБОТА БАКАЛАВРА
ТЕОРЕМИ ЧЕВИ І МЕНЕЛАЯ ТА ЇХ ЗАСТОСУВАННЯ
Виконавець Керівник роботи
студентка групи ММ-01-1 к.ф.-м.н., доцент
Бондаренко Н.С. Поляков О.В.
Допускається до захисту
Завідувач кафедрою Рецензент
доктор фіз.-мат. наук, професор к.ф.-м.н., доцент
Бабенко В.Ф. Великін В.Л.
м. Дніпропетровськ
2006 р.
РЕФЕРАТ
Дипломна робота містить 87 стор., 54 рис., 20 джерел.
Об ’ єктом дослідження є теореми Чеви та Менелая на площині та в просторі.
Мета роботи – вивчення теорем Чеви та Менелая на площині та в просторі, доведення нетривіальних наслідків цих теорем та розв’язання задач двома способами: традиційним і за допомогою теорем Чеви та Менелая.
Одержані висновки та їх новизна – теорема Менелая дозволяє знаходити відношення відрізків, а також доводити належність трьох точок одній прямій. Теореми Чеви та їх наслідки використовується при розв’язуванні задач про трійки прямих, що проходять через одну точку, а також при доведенні теорем про перетин трійок прямих в одній точці. Розглянуто аналоги теорем Чеви та Менелая в просторі. В дипломній роботі розв’язано 50 задач.
Результати досліджень можуть бути застосовані при викладанні теми “Теореми Чеви та Менелая” в математичних класах середніх шкіл, гімназіях та ліцеях, при позакласній роботі з учнями (на заняттях математичних гуртків, при проведенні математичних олімпіад, для індивідуальної роботи з найбільш здатними учнями).
Перелік ключових слів: ТЕОРЕМА ЧЕВИ, ТЕОРЕМА МЕНЕЛАЯ, ТРИКУТНИК, ТЕТРАЕДР, ТОЧКА, ПРЯМА, СІЧНА, ВІДРІЗОК.
ANNOTATION
This degree thesis of the 5th year student (DNU, Faculty of Mechanics and Mathematics, Department of Mathematical Analysis) deals with Cheva’s and Menelay’s theorems. The work is interesting for the students and post-graduates students of mathematical specialties.
Bibliography: 20.
ЗМІСТ
ВСТУП
РОЗДІЛ 1. Теорема Менелая для трикутника
1.1 Орієнтовані відрізки
1.2 Теорема Менелая
1.3 Теореми Дезарга, Паппа, Паскаля, Гаусса
1.4 Застосування теореми Менелая для розв’язання задач
РОЗДІЛ 2. Теорема Менелая для тетраедра
РОЗДІЛ 3. Теореми Чеви для трикутника та тетраедра. Теорема Чеви в формі синусів
3.1 Теореми Чеви для трикутника, тетраедра, в формі синусів
3.2 Застосування теорем Чеви для розв’язання задач
РОЗДІЛ 4. Теореми Чеви та Менелая на площині
ВИСНОВКИ
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ
ВСТУП
Геометрія починається з трикутника. Якщо взяти шкільний підручник з геометрії, то ми побачимо, що перші змістовні теореми стосуються саме трикутника. Все попереднє – лише аксіоми, означення або найпростіші з них наслідки. На початку свого виникнення планіметрія була “геометрією трикутника”. “Геометрія трикутника” може пишатися теоремами, які носять ім’я Ейлера, Торрічеллі, Лейбниця. На рубежі 19-20 століть завдяки великій кількості робіт, присвячених трикутнику, був створений цілий новий розділ планіметрії – “Нова геометрія трикутника”. Багато з цих робіт зараз виглядають малоцікавими, недосконалими; термінологія, яка використовувалась в них майже забута й зустрічається тільки в енциклопедіях. Але деякі теореми “Нової геометрії” продовжують жити й досі. Двом таким теоремам – Чеви та Менелая – присвячена дипломна робота.
Теореми Чеви та Менелая можна назвати “двоїстими” теоремами: вони схоже формулюються й доводяться, вони взаємозамінюються при розв’язанні задач. Теореми Чеви та Менелая корисні у випадках, коли необхідно “з’ясувати відношення” між точками та прямими, – наприклад, довести, що будь-які три прямі перетинаються в одній точці, три точки лежать на одній прямій та ін.
Теореми Чеви та Менелая не входять в основний курс шкільної геометрії, між тим вони прості, цікаві й застосовуються при розв’язанні досить складних задач.
Дипломна робота присвячена розробці методики викладання теми “Теореми Чеви та Менелая та їх застосування”.
Робота складається із вступу, 4 розділів, висновків та списку використаної літератури. Кожен розділ побудовано за такою структурою. На початку розділу наводиться необхідний теоретичний матеріал, потім викладено задачі з докладним розв’язанням, а наприкінці наведено задачі для самостійної роботи з розв’язанням та відповідями.
В першому розділі роботи “Теорема Менелая для трикутника” сформульовано й доведено теорему Менелая для трикутника, наведено нетривіальні приклади використання теореми Менелая (доведено теореми Дезарга, Паппа, Паскаля, Гаусса), продемонстровано ефективність використання теореми на приклади розв’язання задач двома способами: традиційним і за допомогою теореми Менелая.
В другому розділі “Теорема Менелая для тетраедра” сформульовано й доведено аналог теореми Менелая в просторі, наведено приклади розв’язання складних стереометричних задач.
В третьому розділі “Теореми Чеви для трикутника та тетраедра. Теорема Чеви в формі синусів” сформульовані теореми Чеви та наслідки з них, наведено розв’язані задачі.
В четвертому розділі “Теореми Чеви та Менелая для площини” наведено інший підхід до формулювання теорем Чеви та Менелая.
Всього в роботі розв’язано 50 задач.
Дипломна робота може бути використана викладачами ліцеїв та гімназій при викладанні спеціальних курсів, а також при підготовці учнів до олімпіад з математики.
РОЗДІЛ 1
Рис. 1.3
Тоді, якщо точки 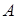 і
і 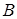 лежать по одну сторону від прямої
лежать по одну сторону від прямої 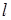 , то відрізки
, то відрізки 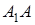 й
й 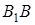 орієнтовані однаково (див. рис. 1.3а), а якщо по різні сторони – протилежно (див. рис. 1.3б), при цьому в обох випадках
орієнтовані однаково (див. рис. 1.3а), а якщо по різні сторони – протилежно (див. рис. 1.3б), при цьому в обох випадках 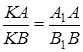 .
.
Зазначемо такі важливі властивості відношень:
1) 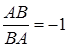 2)
2) 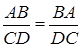 .
.
Нехай тепер на прямій 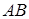 задана ще третя точка –
задана ще третя точка – 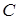 . На рисунку 1.4 показано, якими можуть бути відношення
. На рисунку 1.4 показано, якими можуть бути відношення 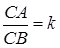 в залежності від положення точки
в залежності від положення точки  на прямій
на прямій 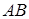 . Так, якщо
. Так, якщо 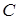 лежить на відрізку
лежить на відрізку 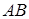 , то
, то 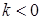 ; якщо точка
; якщо точка  лежить ліворуч від точки
лежить ліворуч від точки 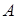 , то
, то 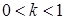 ; якщо точка
; якщо точка 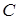 лежить праворуч від точки
лежить праворуч від точки 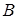 , то
, то 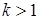 .
.
Отже, задаючи відношення орієнтованих відрізків 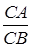 ми однозначно визначаємо положення точки
ми однозначно визначаємо положення точки 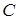 на прямій
на прямій 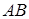 .
.
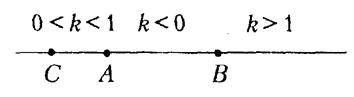 |
Рис. 1.4
Зауваження. Точки 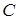 , для якої
, для якої 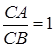 , не має на прямій
, не має на прямій 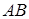 (можна приєднати до прямої нескінчено удалену точку
(можна приєднати до прямої нескінчено удалену точку 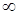 і вважати, що саме для неї
і вважати, що саме для неї 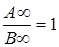 ). Слід зазначити, що просте відношення довжин відрізків
). Слід зазначити, що просте відношення довжин відрізків  неоднозначно задає точку
неоднозначно задає точку 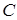 на прямій
на прямій 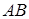 – таких точок, як правило, дві (за виключенням середини відрізка
– таких точок, як правило, дві (за виключенням середини відрізка 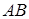 , для якої
, для якої 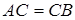 ).
).
Теорема Менелая
Теорема Менелая дійшла до нас в арабському перекладі книги «Сферика» грецького математика та астронома Менелая Олександрійського (І-ІІ століття нашої ери). Теорема Менелая дозволяє в деяких випадках знаходити відношення відрізків, а також доводити належність трьох точок одній прямій.
Теорема Менелая. Нехай задано трикутник  і три точки
і три точки  на прямих
на прямих  і
і 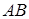 відповідно. Точки
відповідно. Точки 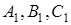 лежать на одній прямій тоді і тільки тоді, коли
лежать на одній прямій тоді і тільки тоді, коли
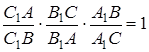 (1.1)
(1.1)
Зауваження. Іноді добуток відношень в теоремі Менелая записують так:
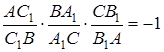
Тут всі відношення, що перемножуються – це відношення орієнтованих відрізків .

Рис. 1.5
Доведення.
Необхідність. Нехай пряма 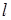 перетинає прямі
перетинає прямі 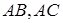 та
та 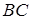 в точках
в точках 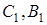 і
і  відповідно (див. рис. 1.5) і
відповідно (див. рис. 1.5) і 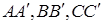 – перпендикуляри, які опущено з точок
– перпендикуляри, які опущено з точок  на пряму
на пряму  . Як було доведено раніше,
. Як було доведено раніше,
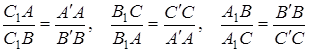 .
.
Перемножаючи записані відношення, маємо
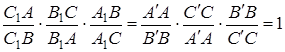 .
.
Достатність. Проведемо пряму 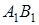 . Ми повинні довести, що ця пряма перетинає
. Ми повинні довести, що ця пряма перетинає 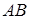 в точці
в точці 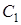 . Насамперед доведемо, що
. Насамперед доведемо, що 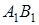 дійсно перетинає
дійсно перетинає 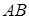 . Припустимо, що
. Припустимо, що 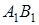 паралельна
паралельна 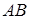 (див. рис. 1.6). Але тоді
(див. рис. 1.6). Але тоді
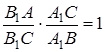
Звідси та з рівності (1.1) випливає 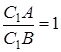 , що неможливо.
, що неможливо.
Нехай 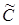 – точка перетину прямих
– точка перетину прямих 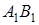 та
та 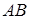 . По вже доведеному
. По вже доведеному
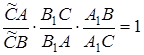
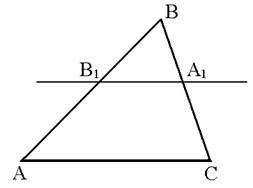
Рис. 1.6
Порівнюючи з умовою, одержуємо, що
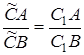 .
.
Оскільки мова йде про відношення орієнтованих відрізків, то 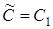 , що потрібно було довести довести. Отже, теорема Менелая повністю доведена.
, що потрібно було довести довести. Отже, теорема Менелая повністю доведена.
Зауваження 1. При розв’язанні конкретних обчислювальних задач, якщо відомо, що точки  і
і  лежать на одній прямій, можна не турбуватися про запис відношень орієнтованих відрізків в формулі (1.1), а обмежитися відношеннями їх довжин.
лежать на одній прямій, можна не турбуватися про запис відношень орієнтованих відрізків в формулі (1.1), а обмежитися відношеннями їх довжин.
Зауваження 2. Якщо замінити в (1.1) орієнтовані відношення відношеннями довжин, обернена теорема перестає бути вірною, тобто точки  і
і  , для яких виконується (1.1), не повинні лежати на одній прямій.
, для яких виконується (1.1), не повинні лежати на одній прямій.
Наприклад, нехай точки 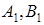 взяті на сторонах
взяті на сторонах 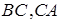 трикутника
трикутника 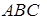 так, що
так, що 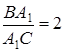 ,
, 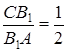 і
і 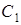 – середина сторони
– середина сторони 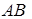 , тоді
, тоді
 ,
,
але точки 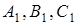 не лежать на одній прямій.
не лежать на одній прямій.
Доведення.
З теореми Менелая для трикутника 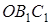 та прямої
та прямої 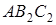 (точка
(точка 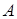 лежить на
лежить на 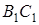 ,
, 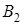 – на
– на 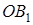 ,
,  – на
– на  ) випливає, що
) випливає, що

Аналогічно, з трикутників 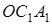 та
та 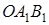 , які перетинаються прямими
, які перетинаються прямими 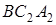 та
та 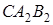 відповідно, маємо
відповідно, маємо
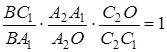 ,
, 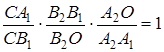
Перемножуючи виписані рівності, після скорочення одержуємо
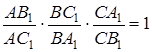
Але точки  лежать на сторонах або продовженнях сторін трикутника
лежать на сторонах або продовженнях сторін трикутника  і згідно з теоремою Менелая лежать на одній прямій.
і згідно з теоремою Менелая лежать на одній прямій.
Теорема доведена.
Наступна теорема була доведена в другій половині ІІІ століття древнегрецьким математиком Паппом Александрійським.
Теорема Паппа. На одній з прямих, що перетинаються взяті точки  , на іншій – точки
, на іншій – точки  (див. рис. 8а). Прямі
(див. рис. 8а). Прямі 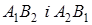 ,
, 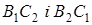 ,
, 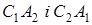 перетинаються в точках
перетинаються в точках 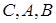 відповідно. Тоді точки
відповідно. Тоді точки  лежать на одній прямій.
лежать на одній прямій.
Доведення.
Розглянемо трикутник 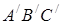 , де
, де 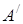 – точка перетину прямих
– точка перетину прямих 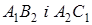 ,
, 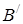 – точка перетину прямих
– точка перетину прямих  ,
, 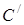 – точка перетину прямих
– точка перетину прямих 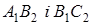 (див. рис. 8б). Точки
(див. рис. 8б). Точки 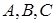 лежать на прямих
лежать на прямих 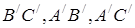 відповідно.
відповідно.
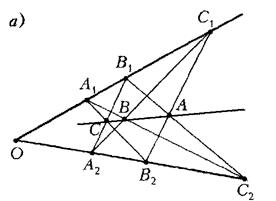
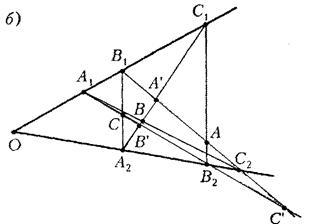
Рис. 1.8
Запишемо теорему Менелая для трикутника 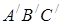 та п’яти прямих
та п’яти прямих 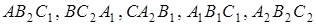 , які перетинають сторони (або їх продовження) цього трикутника. Маємо
, які перетинають сторони (або їх продовження) цього трикутника. Маємо
 та пряма
та пряма  :
: 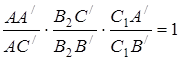 ,
,
 та пряма
та пряма 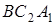 :
: 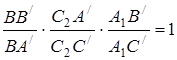 ,
,
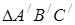 та пряма
та пряма 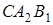 :
:  ,
,
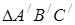 та пряма
та пряма 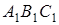 :
: 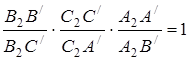 ,
,
 та пряма
та пряма 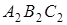 :
: 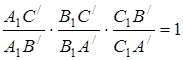 .
.
Перемножуючи одержані рівності, знаходимо
 ,
,
отже, точки 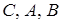 лежать на одній прямій. Теорема доведена.
лежать на одній прямій. Теорема доведена.
Теорема Паскаля. Нехай шестикутник 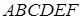 вписано в коло. Тоді точки перетину його протилежних сторін лежать на одній прямій.
вписано в коло. Тоді точки перетину його протилежних сторін лежать на одній прямій.
Доведення.
Нехай 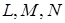 – точки перетину прямих
– точки перетину прямих 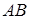 і
і 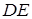 ,
, 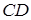 і
і 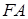 ,
, 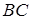 і
і  відповідно, а
відповідно, а  – точки перетину прямих
– точки перетину прямих 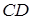 і
і  ,
, 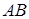 і
і  ,
, 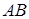 і
і 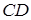 відповідно (див. рис. 1.9). Необхідно довести, що
відповідно (див. рис. 1.9). Необхідно довести, що 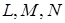 лежать на одній прямій.
лежать на одній прямій.
Застосуємо теорему Менелая до трикутника 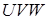 та прямої
та прямої 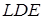 :
:
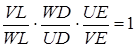 .
.
Застосуємо теорему Менелая до трикутника 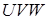 та прямої
та прямої 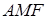 :
:
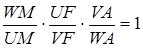 .
.
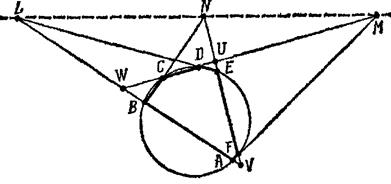
Рис. 1.9
Застосуємо теорему Менелая до трикутника  та прямої
та прямої  :
:
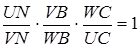 .
.
Перемножуючи ці рівності, маємо
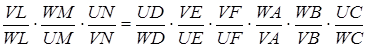
Використаємо властивості відрізків січних:
 ,
,  ,
, 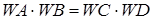 .
.
Звідси маємо
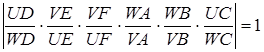 ,
,
а оскільки знак кожного з шести співмножників від’ємний, то
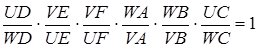 ,
,
тому
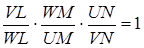 ,
,
отже точки  лежать на одній прямій.
лежать на одній прямій.
Теорема доведена.
Теорема Гаусса. Середина відрізка, що з’єднує точки перетину продовжень протилежних сторін чотирикутника, лежить на прямій, що проходить через середини діагоналей чотирикутника.
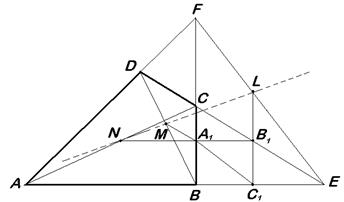
Рис. 1.10
Доведення
Нехай протилежні сторони чотирикутника  перетинаються в точках
перетинаються в точках 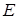 та
та 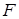 (див. рис. 1.10). необхідно довести, що середина
(див. рис. 1.10). необхідно довести, що середина 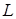 відрізка
відрізка  , середини
, середини 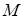 та
та 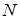 діагоналей
діагоналей 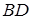 і
і 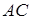 чотирикутника
чотирикутника  лежать на одній прямій.
лежать на одній прямій.
Через точки 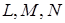 проведемо прямі, паралельні сторонам трикутника
проведемо прямі, паралельні сторонам трикутника 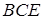 :
: 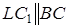 ,
,  ,
,  .
.
Згідно з теоремою Фалеса ці прямі перетинають сторони 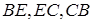 трикутника
трикутника  в їх серединах
в їх серединах 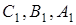 . Таким чином, точки
. Таким чином, точки 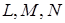 лежать на продовженнях сторін трикутника
лежать на продовженнях сторін трикутника 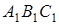 , сторони якого є середніми лініями трикутника
, сторони якого є середніми лініями трикутника 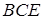 . Для того, щоб довести, що точки
. Для того, щоб довести, що точки 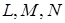 лежать на одній прямій, достатньо довести співвідношення
лежать на одній прямій, достатньо довести співвідношення
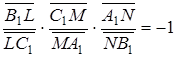 .
.
В силу властивості середньої лінії трикутника
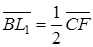 ,
, 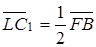 .
.
Отже, 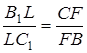 . Аналогічно знаходимо
. Аналогічно знаходимо 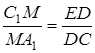 ,
, 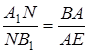 . Тоді добуток
. Тоді добуток 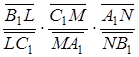 дорівнює
дорівнює 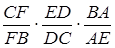 . А цей добуток дорівнює –1 згідно з теоремою Менелая, яка застосовується до
. А цей добуток дорівнює –1 згідно з теоремою Менелая, яка застосовується до 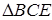 та прямої
та прямої 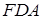 . Теорема доведена.
. Теорема доведена.
РОЗДІЛ 2
РОЗДІЛ 3
Доведення.
Необхідність. Нехай через деяку точку 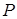 проходять три прямі як показано на рисунку 3.1. Застосуємо теорему Менелая до трикутника
проходять три прямі як показано на рисунку 3.1. Застосуємо теорему Менелая до трикутника 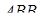 , який перетинає пряма
, який перетинає пряма 
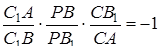 .
.
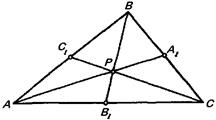
Рис. 3.1 До формуліровки теореми Чеви
Аналогічно з трикутника  згідно з теоремою Менелая маємо
згідно з теоремою Менелая маємо
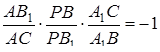 .
.
Розділимо перше співвідношення на друге
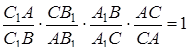
Залишилося помітити, що
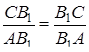 і
і 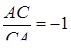
Необхідність доведена для випадку прямих, що перетинаються.
Якщо ж прямі 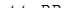 і
і  паралельні (див. рис. 3.2), то згідно з теоремою Фалеса маємо
паралельні (див. рис. 3.2), то згідно з теоремою Фалеса маємо
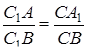 ,
,
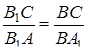 .
.
Перемножуючи пропорції, одержимо
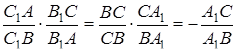
тобто
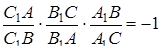 .
.
Необхідність доведена в повному обсязі.
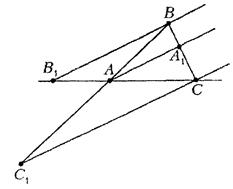
Рис. 3.2 До доведення теореми Чеви
Достатність. Нехай для точок  і
і  на прямих
на прямих  і
і 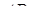 виконується співвідношення (3.1), а прямі
виконується співвідношення (3.1), а прямі 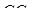 і
і 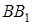 перетинаються в точці
перетинаються в точці 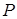 . Пряма
. Пряма 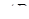 перетинає прямую
перетинає прямую 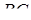 в деякій точці
в деякій точці 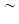 . По вже доведеному
. По вже доведеному
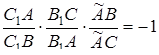 .
.
Звідси й зі співвідношення (3.1) випливає 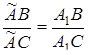 , що означає збіг точок
, що означає збіг точок 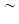 і
і  .
.
Якщо ж прямі  і
і 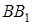 паралельні, то з (3.1) випливає, що і пряма
паралельні, то з (3.1) випливає, що і пряма 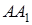 буде їм паралельна. Теорема доведена.
буде їм паралельна. Теорема доведена.
Доведення.
1) Оскільки 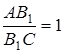 ,
, 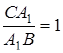 ,
, 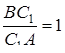 , то
, то  , отже медіани трикутника перетинаються в одній точці.
, отже медіани трикутника перетинаються в одній точці.
2) Розглянемо випадок, коли трикутник  гострокутний.
гострокутний.
Маємо 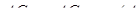 ,
, 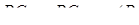 ,
, 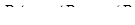 ,
, 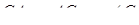 ,
, 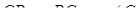 ,
, 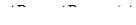 .
.
Звідси випливає
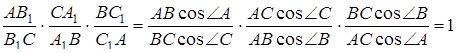
Якщо трикутник  тупокутний, то дві висоти цього трикутника не є чевіанами. У випадку, коли точно один з відрізків
тупокутний, то дві висоти цього трикутника не є чевіанами. У випадку, коли точно один з відрізків 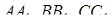 є чевіаною, а інші з’єднують вершини з точками продовжень протилежних сторін, при цьому ці відрізки не паралельні, твердження теореми Чеви також виконується. Залишається повторити проведені вище обчислення для тупокутного трикутника.
є чевіаною, а інші з’єднують вершини з точками продовжень протилежних сторін, при цьому ці відрізки не паралельні, твердження теореми Чеви також виконується. Залишається повторити проведені вище обчислення для тупокутного трикутника.
3) З властивості бісектрис випливають наступні рівності:
 ,
, 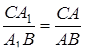 ,
, 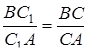 .
.
Перемножуючи відповідно ліві та праві частини цих рівностей, одержуємо умову теореми Чеви.
4) З властивостей дотичних, проведених з однієї точки до кола маємо:
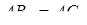 ,
, 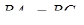 ,
,  .
.
Звідси випливає рівність з теореми Чеви:  .
.
5)
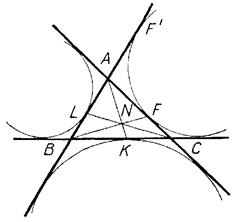
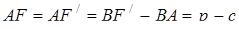 , де
, де 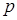 - півпериметр трикутника
- півпериметр трикутника  ,
,
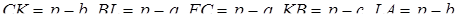 ,
,
Отже,  .
.
Це і означає, що прямі  перетинаються в одній точці.
перетинаються в одній точці.
6) Нехай  – сторони трикутника
– сторони трикутника 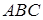 . Нехай
. Нехай 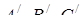 – вершини правильних трикутників, побудованих на сторонах
– вершини правильних трикутників, побудованих на сторонах 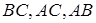 відповідно, а
відповідно, а 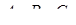 – точки перетину відрізків
– точки перетину відрізків 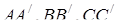 з відповідними сторонами або їх продовженнями. Зазначимо, що
з відповідними сторонами або їх продовженнями. Зазначимо, що
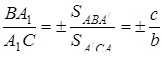 ,
,
при цьому знак “мінус” береться в тому випадку, коли точка 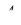 лежить зовні відрізка
лежить зовні відрізка 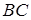 . Аналогічно розписуються відношення для точок
. Аналогічно розписуються відношення для точок 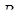 та
та 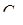 . Після перемноження маємо
. Після перемноження маємо 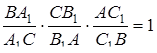 . Наслідки доведено.
. Наслідки доведено.
Іноді теорему Чеви зручно використовувати, вводячи замість відношень відрізків відношення синусів деяких кутів.
Теорема Чеви в формі синусів. Нехай на сторонах  і
і  трикутника
трикутника 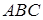 взяті точки
взяті точки 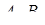 ,
, 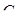 . Прямі
. Прямі  і
і 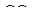 проходять через одну точку або паралельні тоді і тільки тоді, коли
проходять через одну точку або паралельні тоді і тільки тоді, коли
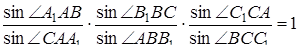 . (3.3)
. (3.3)
Доведення.
Ми повинні переписати “в синусах” теорему Чеви. Запишемо її у формі (3.2):
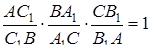 .
.
Доведемо цю теорему для випадку, коли точки 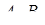 і
і  лежать на сторонах трикутника. Випадки іншого розташування точок вимагають несуттєвих змін міркувань.
лежать на сторонах трикутника. Випадки іншого розташування точок вимагають несуттєвих змін міркувань.
Нехай  .
.
Інші позначення зрозумілі з рисунка 3.3.
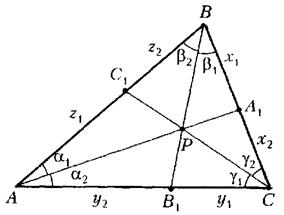
Рис. 3.3 До доведення теорими Чеви у формі синусів
Застосовуючи теорему синусів до трикутників  і
і  , маємо
, маємо
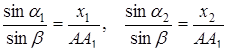
Або
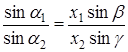
Аналогічно, застосовуючи теорему синусів до трикутників 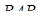 і
і 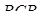 , маємо
, маємо
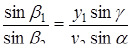 ,
,
і до трикутників 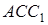 і
і 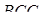 :
:
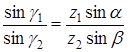 .
.
Перемножуючи записані співвідношення, знаходимо
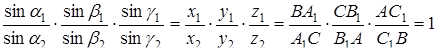
Отже, умова нашої теореми рівносильна умові звичайної теореми Чеви.
Теорема доведена.
При доведенні теореми ми не застосовували відношень орієнтованих відрізків. В загальному випадку необхідно розглянути не тільки орієнтовані відрізки, але й орієнтовані кути, припускаючи, наприклад, що 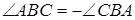 і т.п.
і т.п.
Далі наведемо мало відому стереометричну теорему Чеви для довільного тетраедра.
Т еорема Чеви для тетраедра. Нехай  – точка всередині тетраедра
– точка всередині тетраедра  ,
, 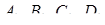 – точки перетину площин
– точки перетину площин  з ребрами
з ребрами  відповідно (див. рис. 3.4). Тоді
відповідно (див. рис. 3.4). Тоді
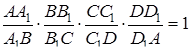 (3.4)
(3.4)
І навпаки, якщо для точок  , що лежать на відповідних ребрах, виконується співвідношення (3.4), то площини
, що лежать на відповідних ребрах, виконується співвідношення (3.4), то площини  проходять через одну точку.
проходять через одну точку.
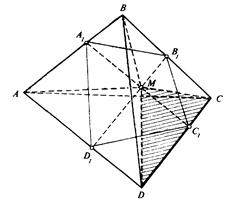
Рис. 3.4 До формуліровки теореми Чеви для тетраедра
Доведення необхідності легко одержати, якщо помітити, що точки  (див. рис. 3.4) лежать в одній площині (це площина, що проходить через прямі
(див. рис. 3.4) лежать в одній площині (це площина, що проходить через прямі 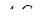 та
та 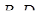 , які перетинаються в точці
, які перетинаються в точці  ), і застосувати теорему Менелая.
), і застосувати теорему Менелая.
Обернена теорема доводиться так само, як і обернена теорема Менелая в просторі: необхідно провести площину через точки 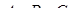 і довести, що ця площина перетне ребро
і довести, що ця площина перетне ребро 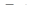 в точці
в точці 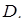 .
.
Доведення.
Нехай прямі, які проходять через вершини трикутника 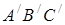 перпендикулярно до відповідних сторін трикутника
перпендикулярно до відповідних сторін трикутника 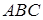 , перетинаються в точці
, перетинаються в точці 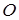 .
.
Оскільки точки 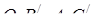 лежать на колі, побудованому на відрізку
лежать на колі, побудованому на відрізку 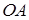 як на діаметрі, то
як на діаметрі, то  . Опустимо з точки
. Опустимо з точки 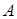 перпендикуляр
перпендикуляр 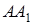 на пряму
на пряму  . Оскільки
. Оскільки 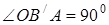 , то
, то 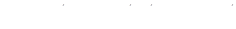 , тобто пряма
, тобто пряма 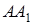 симетрична прямій
симетрична прямій 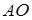 відносно бісектриси кута
відносно бісектриси кута 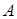 .
.
Аналогічні міркування для інших кутів показують, що перпендикуляри  , які опущені з вершин трикутника
, які опущені з вершин трикутника 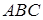 на сторони трикутника
на сторони трикутника 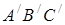 симетричні прямим
симетричні прямим  відносно бісектрис трикутника
відносно бісектрис трикутника 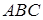 . Згідно з задачею 3.9 прямі
. Згідно з задачею 3.9 прямі  перетинають в одній точці.
перетинають в одній точці.
Задача 3.18 (теорема Ван Обеля). На сторонах  трикутника
трикутника 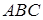 взято точки
взято точки  , так що прямі
, так що прямі 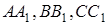 перетинаються в одній точці. Довести, що
перетинаються в одній точці. Довести, що
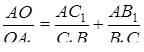 .
.
Доведення.
Нехай прямі  перетинають пряму, яка проходить через точку
перетинають пряму, яка проходить через точку 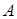 паралельно прямій
паралельно прямій 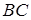 , в точках
, в точках  і
і 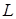 .
.

Оскільки трикутник  подібний до трикутника
подібний до трикутника  , трикутник
, трикутник 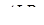 подібний до трикутника
подібний до трикутника  за першою ознакою подібності трикутників, то
за першою ознакою подібності трикутників, то  ;
; 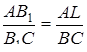 . Додавши ці рівності і, враховуючи, що
. Додавши ці рівності і, враховуючи, що 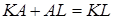 , одержуємо:
, одержуємо:
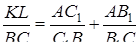 .
.
Далі, трикутник  подібний до трикутника
подібний до трикутника 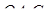 і трикутник
і трикутник 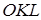 подібний до трикутника
подібний до трикутника 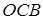 .
.
Тому  ;
; 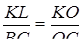 .
.
Звідси випливає, що 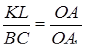 . З цієї рівності і рівності
. З цієї рівності і рівності  безпосередньо випливає, що
безпосередньо випливає, що
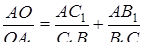 .
.
Задача 3. 19 Задано трикутник 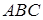 . Довести, що чевіани
. Довести, що чевіани 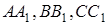 , які ділять його периметр навпіл, перетинаються в одній точці.
, які ділять його периметр навпіл, перетинаються в одній точці.
Доведення.
Нехай довжини сторін 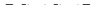 відповідно
відповідно  , тоді число
, тоді число 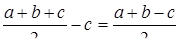 згідно з нерівністю трикутника додатнє і менше
згідно з нерівністю трикутника додатнє і менше 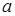 .
.
Нехай точка  лежить на стороні
лежить на стороні 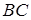 і така, що
і така, що 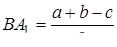 . Зрозуміло, що пряма
. Зрозуміло, що пряма 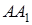 ділить периметр трикутника
ділить периметр трикутника 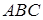 навпіл, аналогічно з точками
навпіл, аналогічно з точками  і
і  (можна помітити, що
(можна помітити, що  – точки дотику вневписаних кіл трикутника
– точки дотику вневписаних кіл трикутника 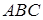 ).
).
Переконавшись в існуванні потрібних точок, розв’яжемо основну задачу.
Для цього обчислюємо довжини всіх необхідних відрізків.
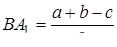 ,
, 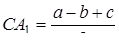 ,
, 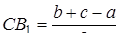 ,
,
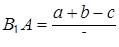 ,
, 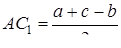 ,
,  .
.
Зрозуміло, що 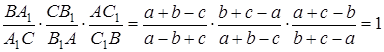 , отже чевіани
, отже чевіани 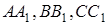 перетинаються в одній точці.
перетинаються в одній точці.
РОЗДІЛ 4
Доведення теореми Чеви.
Необхідність. Нехай прямі 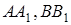 ,
, 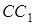 перетинаються в одній точці. Доведемо, що виконуються умови (4.5) і (4.5/).
перетинаються в одній точці. Доведемо, що виконуються умови (4.5) і (4.5/).
Якщо прямі 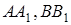 і
і 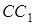 перетинаються в одній точці, то або всі три точки
перетинаються в одній точці, то або всі три точки  і
і 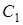 лежать на сторонах трикутника
лежать на сторонах трикутника 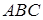 , або одна з точок лежить на стороні трикутника, а дві інші – на продовженнях відповідних сторін.
, або одна з точок лежить на стороні трикутника, а дві інші – на продовженнях відповідних сторін.
У першому випадку всі дроби, що входять у вираз 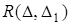 , додатні, а в другому випадку один із трьох дробів, що входить у вираз
, додатні, а в другому випадку один із трьох дробів, що входить у вираз 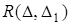 , додатний, а два інші – від’ємні, так що знову вираз
, додатний, а два інші – від’ємні, так що знову вираз 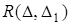 (а отже, і
(а отже, і  – див. лему) більше нуля.
– див. лему) більше нуля.
Доведемо, що  (оскільки
(оскільки  >0, то з цього буде випливати, що
>0, то з цього буде випливати, що 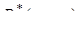 дорівнює одиниці).
дорівнює одиниці).
Позначимо точку перетину прямих 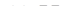 і
і 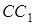 через
через 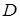 (рис. 4.4а).
(рис. 4.4а).
а) 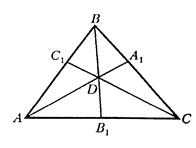
б) 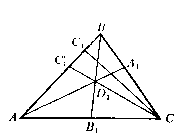
Рис. 4.4
Застосовуючи теорему синусів, одержимо
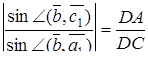 ,
,
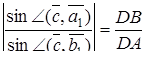
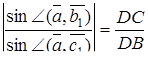
Перемножуючи ці рівності, знаходимо 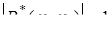 , тим самим необхідність доведена.
, тим самим необхідність доведена.
Достатність. Доведення достатності проведемо методом від супротивного.
Припустимо, що 
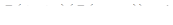 , але прямі
, але прямі  ,
, 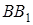 і
і 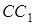 не проходять через одну крапку (див. рис. 4.4б).
не проходять через одну крапку (див. рис. 4.4б).
Позначимо точку перетину прямих 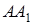 і
і 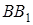 через
через 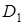 , а через
, а через 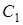 – точку перетину прямих
– точку перетину прямих 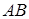 і
і 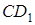 . Оскільки прямі
. Оскільки прямі 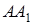 ,
, 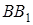 і
і 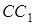 перетинаються в одній точці, то
перетинаються в одній точці, то
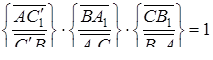
Але за умовою
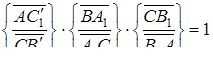 ,
,
звідки 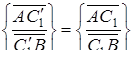 . Так як і точка
. Так як і точка 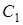 і точка
і точка 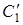 лежать на прямій
лежать на прямій 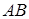 , то з цього випливає, що точки
, то з цього випливає, що точки 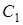 та
та 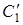 збігаються.
збігаються.
Теорема Чеви доведена.
Доведення теореми Менелая
Необхідність. Відомо, що точки  і
і 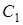 лежать на одній прямій. Необхідно довести рівності (4.6) та (4.
лежать на одній прямій. Необхідно довести рівності (4.6) та (4. 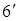 ).
).
Якщо точки  і
і 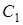 лежать на одній прямій, то або усі вони знаходяться на продовженнях
лежать на одній прямій, то або усі вони знаходяться на продовженнях 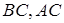 і
і 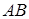 сторін трикутника
сторін трикутника 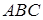 , або ж дві з точок
, або ж дві з точок 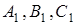 знаходяться на відповідних ним сторонах, а третя – на продовженні.
знаходяться на відповідних ним сторонах, а третя – на продовженні.
В обох випадках вираження 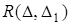 буде від’ємним. Доведемо тепер, що якщо точки
буде від’ємним. Доведемо тепер, що якщо точки 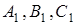 – на одній прямій, то
– на одній прямій, то  (оскільки
(оскільки 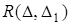 <0, з цього буде випливати, що
<0, з цього буде випливати, що 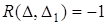 ).
).
Проведемо через точку  пряму, паралельну
пряму, паралельну 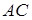 , і позначимо точку її перетину з прямою
, і позначимо точку її перетину з прямою 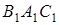 через
через 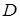 (див. рис. 4.5).
(див. рис. 4.5).
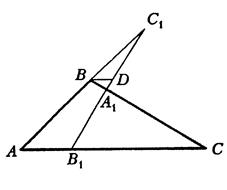
Рис. 4.5
Використовуючи подібність, одержимо
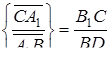
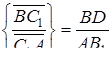
Додавши рівність 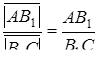 і перемноживши всі три рівності, одержимо, що
і перемноживши всі три рівності, одержимо, що  . Необхідність умов теореми Менелая доведена.
. Необхідність умов теореми Менелая доведена.
Достатність. Доведення достатності умов (4.6) і (4.  ) теореми Менелая проводиться аналогічно доведенню достатності умов (4.5) і (4.
) теореми Менелая проводиться аналогічно доведенню достатності умов (4.5) і (4.  ) теореми Чеви.
) теореми Чеви.
Теорема доведена.
ВИСНОВКИ
Міністерство освіти і науки України
Дніпропетровський національний університет
Механіко-математичний факультет
Кафедра математичного аналізу
ДИПЛОМНА РОБОТА БАКАЛАВРА
Дата: 2019-05-28, просмотров: 314.