Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

1) Мнимая единица. Степень мнимой единицы.

2) Множество комплексных чисел, их геометрическая интерпретация

3) Модуль и аргумент комплексного числа.

4) Действия над комплексными числами в алгебраической форме (сложение, вычитание, умножение, деление, возведение во вторую и третью степень).

5) Элементарные вычисления с помощью МК.

 

х² + 4 = 0       х² = - 4          во множестве R решений нет

                     

Обозначим:

 

   

 

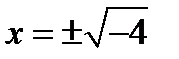
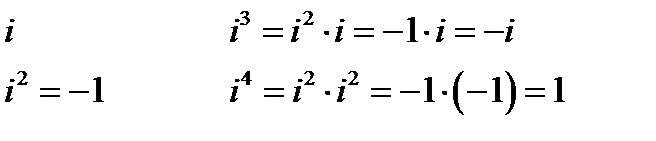
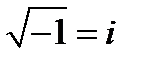
Множество действительных чисел и мнимая единица составляют множество комплексных чисел, тогда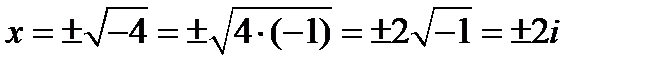

 

i ²³ = i ³ = - i                (23 : 4 = 4  5 + 3)

 

i ²³ = i ²⁰  i ³ = 1  (-i) = - i

 

i ⁴⁸ = i ⁰ = 1      i ¹⁰  i ⁸ i ²  = 1 (-1) = -1 i ¹⁴ = i ² = - 1            i ²⁵ = i ¹ = i

 

i ¹⁰³ = i ³ = - i             2 i ³ - 7 i ⁸ + 5 i ⁹ + 4 i ¹⁰ = - 2 i - 7 + 5 i - 4 = - 11 + 3 i

 

Число Z = a + b i - комплексное число (алгебраическая форма записи)

а - действительная часть числа

b i - мнимая часть числа

a + b i = a1  + b1 i         если а = а1 b = b1

 

a + b i  и  a - b i называются сопряженными

 

 

Например

 

2 - 3 i и 2 + 3 i

 

- 4 - i и - 4 + i ,    т. е. отличаются знаком перед мнимой частью

 

Числа a + b i  и - a - b i   называются противоположными

 

 

Например

 

- 3 - 4 i и 3 + 4 i

 

- 5 + 2 i и 5 - 2 i ,    т.е. отличаются знаками и перед мнимой и перед действительной частями

Комплексные числа изображаются геометрически точкой (a; b) или радиусом - вектором, проведенным к этой точке из начала координат

(-2;3)

0

-2

3

x

y

z4

z3

z2

5i

2

-3

-4i

z1

Z 1 = 5i Z 2 = 2 Z 3 = - 3i           Z 4 = - 4i

-4

3

0

(3;-4)

Z = 3 - 4 i        Z = - 2 + 3 i

 

Изобразите числа:

 

Z = - 7 + 2 i                             Z = - 9 - i

 

Z = - 1 - 4 i                             Z = 12

 

Z = - 5 i                                  Z = 6 i

 

Z = - 4                                   Z = - 3 - 2 i

 

Итак: a + bi

r

r

r

(-a;b)

(a;b)

(a;-b)

(-a;-b)

r

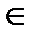a  OX                                                                                                                     I ч j > 0 острый

 

b 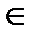 OY                                                                                                II ч j > 0 тупой j = 180 ⁰ - j₁

 

             III ч j < 0; тупой j = - (180 ⁰ - j₁)

 

                                              IV ч j < 0; острый

 

 

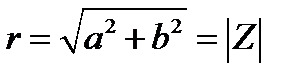 – модуль комплексного числа

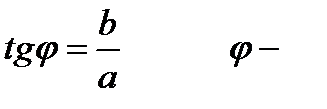 аргумент комплексного числа

 

Найти модуль и аргумент комплексного числа:

 

2

5

x

0

y

а) Z = 5 + 2 i

 

   

 

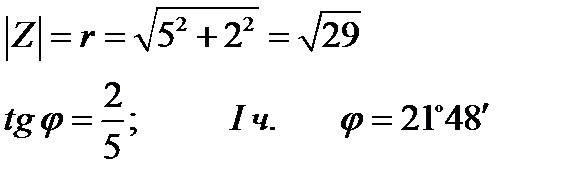
-3

7

x

0

y

б)  Z = - 3 + 7 i

 

 

 

 

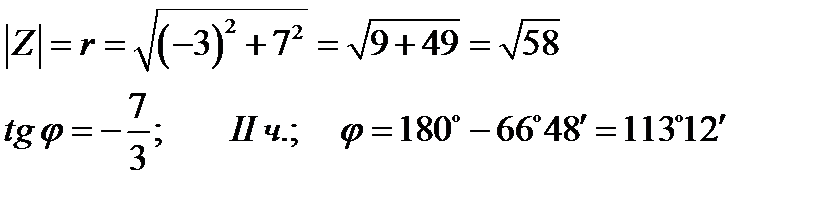
-5

0

-1

x

y

в) Z = - 5 - i

 

     

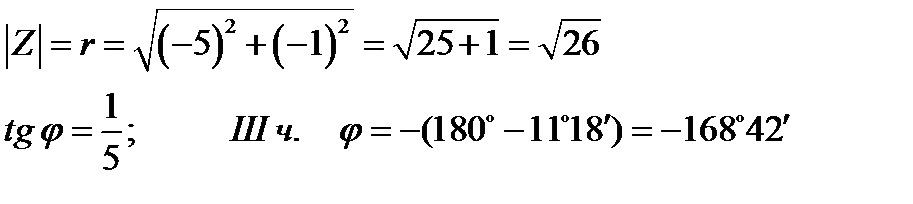
3

-5

0

x

y

 

г) Z = 3 - 5 i

 

      

 

 

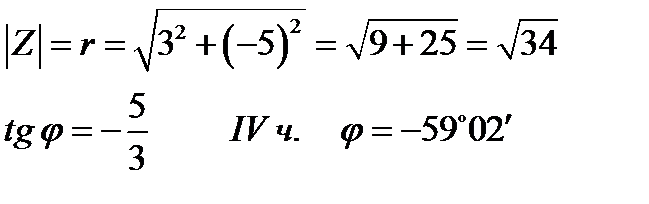
Для чисел, состоящих только из мнимой или только действительной частей нахождение 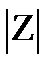 и 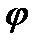    упрощается:

 

2

x

y

0

1) Z = 2             

 

2 = 2 + 0i                 Число находится на "ОХ"

 

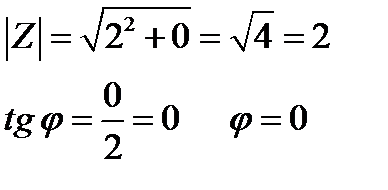
3

y

0

x

2) Z = 3i                               

 

3i = 0 + 3i                          Число находится на "ОУ"

 

 

-4

y

0

x

3) Z = - 4         

 

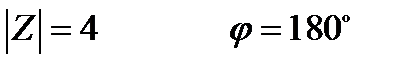  Число находится на "ОХ" (влево)

 

-7

y

0

x

4) Z = - 7 i

 

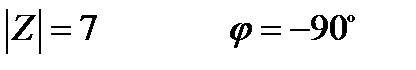 Число находится на "ОУ" (вниз)

Рассмотрим действия над числами

Сложение

Z ₁ + Z ₂ = (a ₁ + b ₁ i) + (a ₂ + b ₂ i) = a ₁ + b ₁ i + a ₂ + b ₂ i = (a ₁  + a ₂) + (b ₁ + b ₂) i

 

Вычитание

Z ₁ - Z ₂ = (a ₁ + b ₁ i) - (a ₂ + b ₂ i) = a ₁ + b ₁ i - a ₂ - b ₂ i = (a ₁  - a ₂) + (b ₁ - b ₂) i

Умножение

Z ₁ Z ₂ = (a ₁ + b ₁ i) (a ₂ + b ₂ i) = a ₁  a ₂ + b ₁ а ₂ i + a ₁ b ₂ i + b ₁ b ₂ i ² =

 

= a ₁ a ₂  + i (b ₁ а ₂  + a ₁ b ₂) - b ₁ b ₂ = (a ₁ a ₂  - b ₁ b ₂) + (b ₁ а ₂  + a ₁ b ₂) i

Например

1) (3 - 5 i) (- 3 + i) = - 9 + 15 i + 3 i - 5 i ² = - 9 +18 i + 5 = - 4 + 18i;

 

                             т.к. i ² = - 1, то -5 (-1) = 5

 

 

2) (2 - 3 i) (2 + 3 i) = 4 - 9 i ² = 4 + 9 = 13

 

 

( a + b i ) ( a - b i ) = a ² - b ²  i ²   = a ² + b ²

( a + b i ) ( a - b i ) = a 2 + b 2

 Сумма квадратов

 

Сумма квадратов разлагается на множители только во множестве комплексных чисел

Деление

 

 

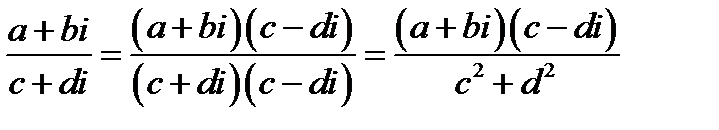
конкретно на примере:

 

 

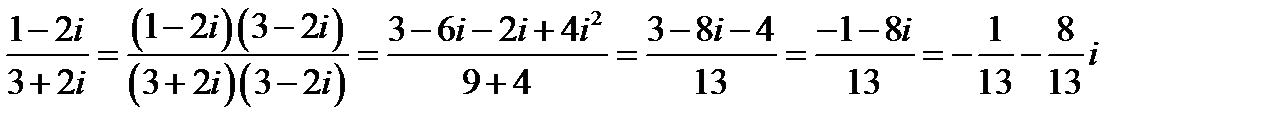
Возведение в квадрат, куб (используем формулы сокращенного умножения)

 

Z = ( a + b i ) ² = a ² + 2 a b i + b ² i ² = a ² + 2 a b i - b ²;

 

например:

 

1)  ( - 4 + i ) ² = 16 - 8 i + i ² = 16 - 8 i - 1 = 15 - 8 i

 

2)  ( 2 - 3 i ) ³ = 8 - 3 2² 3 i + 3 2 ( - 3 i ) ² - 27 i ³ = 8 - 36 i + 54 i ² - 27 i ³ =

 

                        = 8 - 36 i - 54 + 27 i = - 46 - 9 i

 

Выполнить действия

 

 

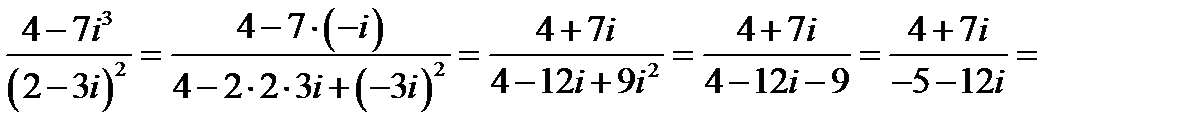
при этих действиях использованы правила: i ³ = - i; i ² = - 1; ( a - b ) ² = a ² - 2 a b + b ² , а теперь разделим, для этого умножим знаменатель на сопряженное ему число ( - 5 + 12 i) , а чтобы дробь не изменилась умножаем и числитель на это число, т.е.

 

 

 

Тема 8. Размещения, перестановки, сочетания. Классическое определение вероятности.