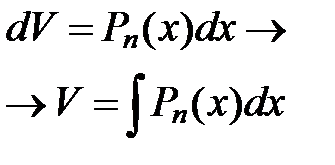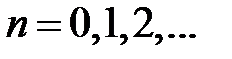Функция F(x) называется первообразной функцией функции f(x) на отрезке [a, b], если в любой точке этого отрезка верно равенство:
F¢(x) = f(x).
Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.
F1(x) = F2(x) + C.
Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением:
F(x) + C.
Записывают: 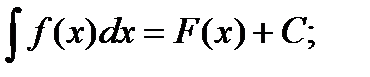
Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.
Свойства:
1. 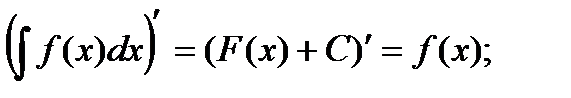
2. 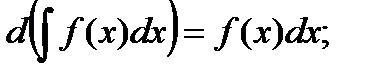
3. 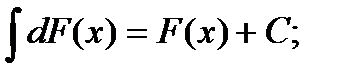
4. 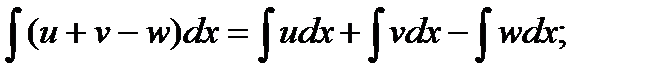 где u, v, w – некоторые функции от х.
где u, v, w – некоторые функции от х.
5. 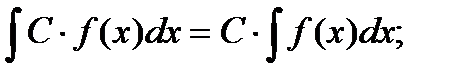
1. 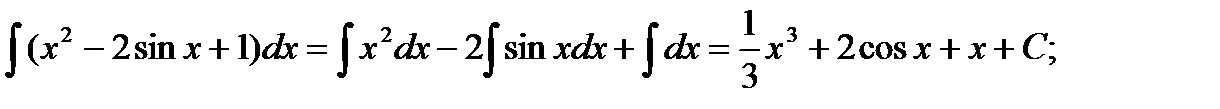
| Интеграл | Значение | Интеграл | Значение | ||
| 1 | 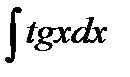
| -ln½cosx½+C | 9 | 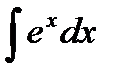
| ex + C |
| 2 | 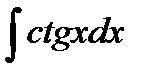
| ln½sinx½+ C | 10 | 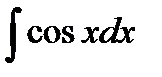
| sinx + C |
| 3 | 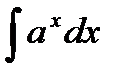
| 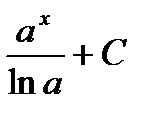
| 11 | 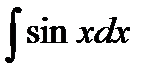
| -cosx + C |
| 4 | 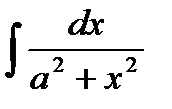
| 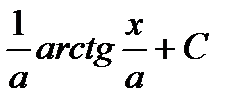
| 12 | 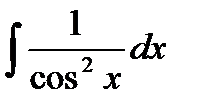
| tgx + C |
| 5 | 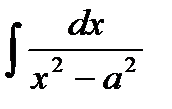
| 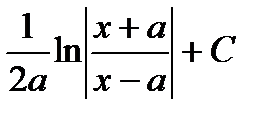
| 13 | 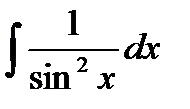
| -ctgx + C |
| 6 | 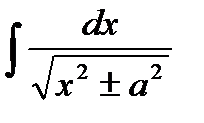
| ln 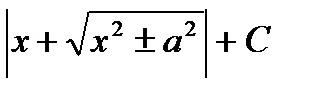
| 14 | 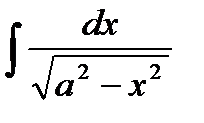
| arcsin 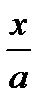 + C + C
|
| 7 | 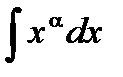
| 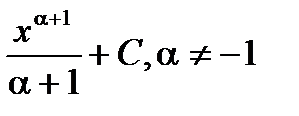
| 15 | 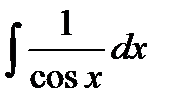
| 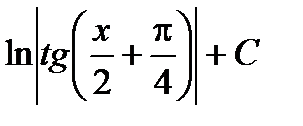
|
| 8 | 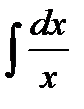
| 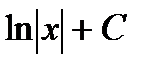
| 16 | 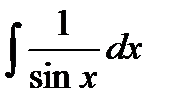
| 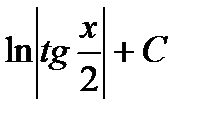
|
Непосредственное интегрирование.
1. 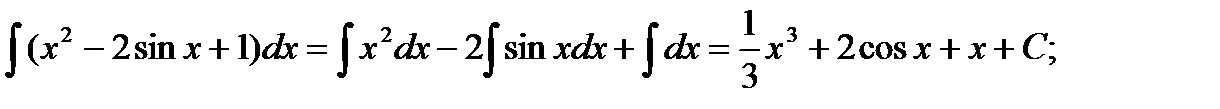
Это интеграл от алгебраической суммы функций.
Применяя свойства интеграла, получим: 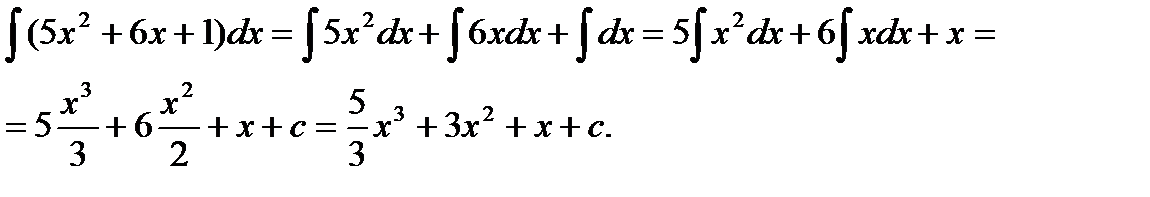
Проверим результат дифференцированием:
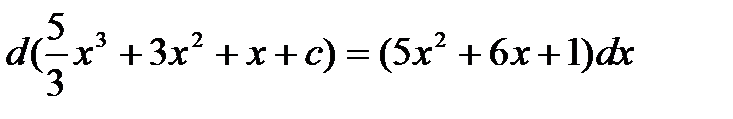 .
.
3. 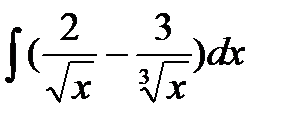 .
.
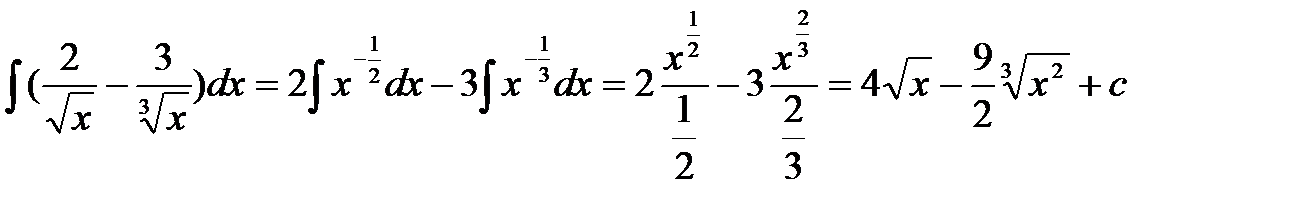 .
.
Проверка. Продифференцируем полученное выражение:
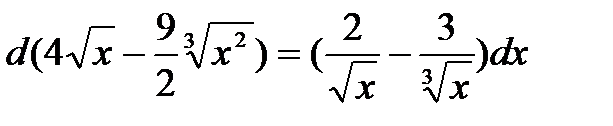 .
.
4. 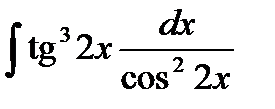 .
.
Преобразуем дифференциал.
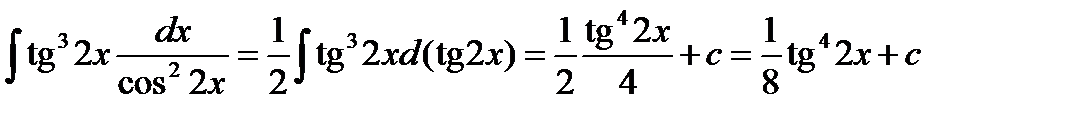 .
.
5. 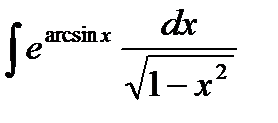 .
.
Преобразуем дифференциал.
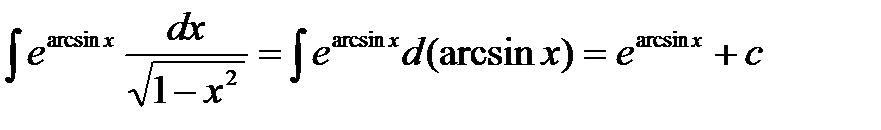 .
.
5. Найти неопределенный интеграл 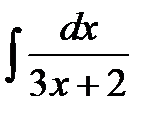 .
.
Преобразуем дифференциал.
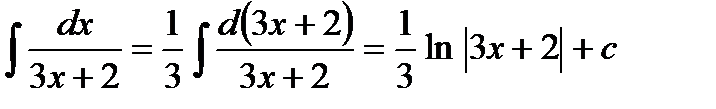 .
.
Метод замены переменной
Теорема 1. Пусть 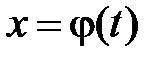 монотонная, непрерывно дифференцируемая функция, тогда
монотонная, непрерывно дифференцируемая функция, тогда
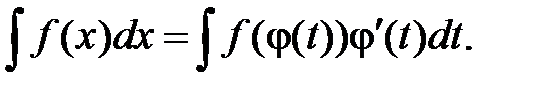 (1)
(1)
При этом, если 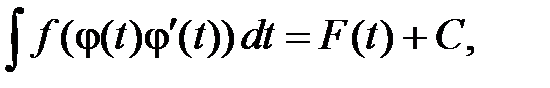 то
то 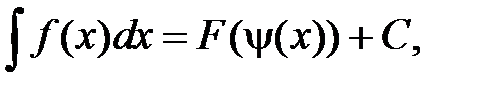 где
где 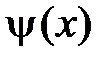 — функция, обратная
— функция, обратная 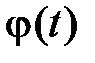 .
.
Формула (1) называется формулой замены переменной в неопределенном интеграле.
Алгоритм замены переменной:
1) Связать старую переменную интегрирования 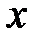 с новой переменной
с новой переменной 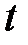 с помощью замены
с помощью замены 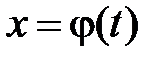 .
.
2) Найти связь между дифференциалами 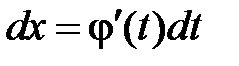 .
.
3) Перейти под знаком интеграла к новой переменной.
4) Проинтегрировать и в полученной первообразной вернуться к старой переменной, подставив 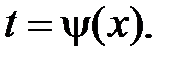
Пример 2. Проинтегрировать подходящей заменой переменной.
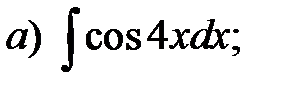
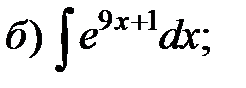
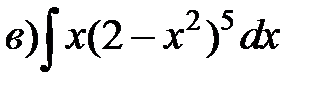
Решение:
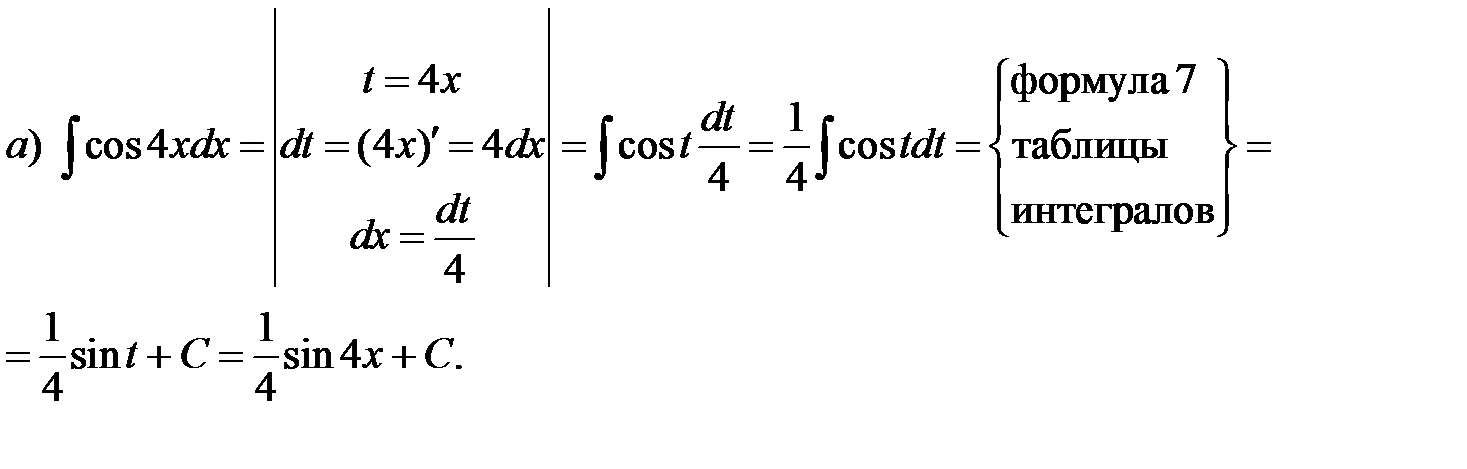
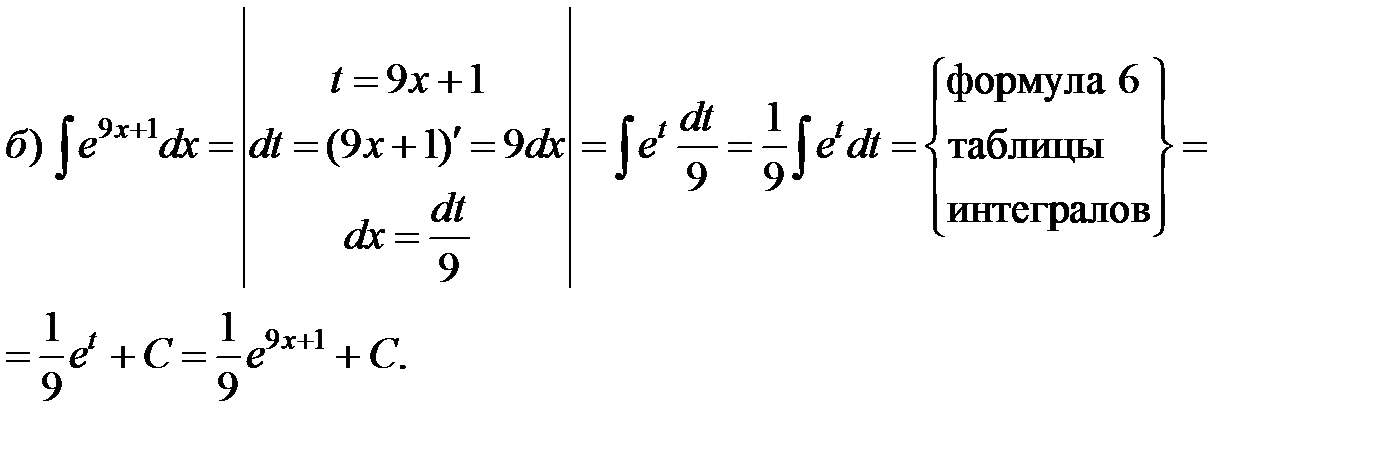
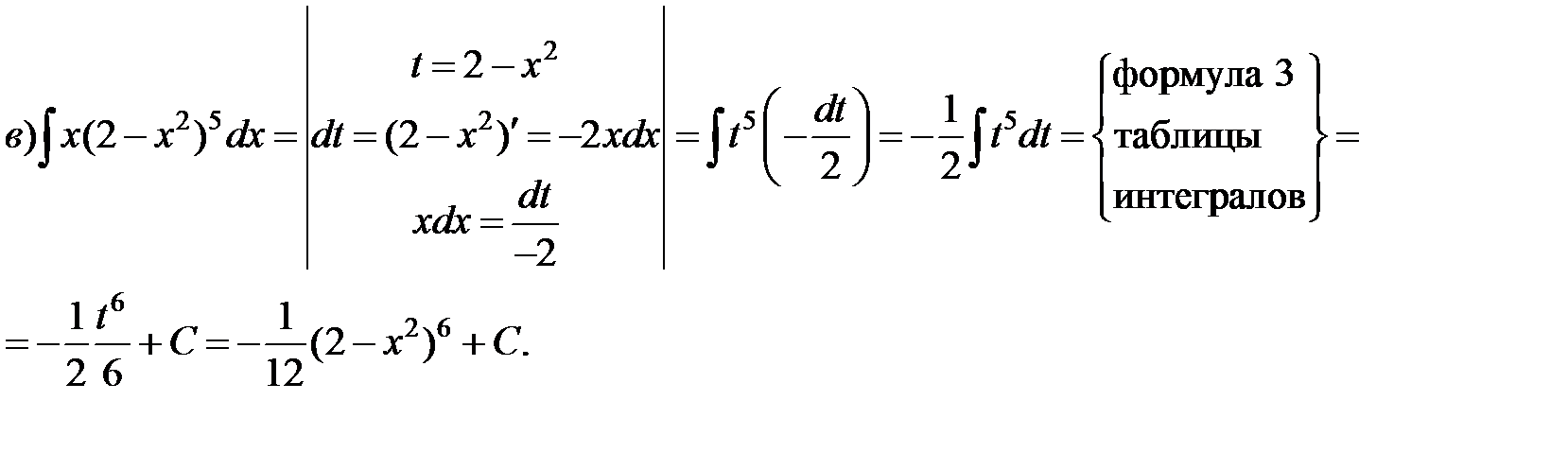
Интегрирование по частям.
Некоторые виды интегралов, вычисляемых по частям
Если производные функций 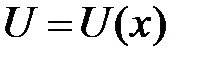 и
и 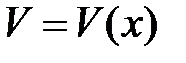 непрерывны, то справедлива формула:
непрерывны, то справедлива формула:

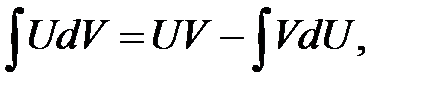 (3)
(3)
называемая формулой интегрирования по частям.
В качестве 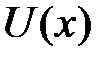 обычно выбирают функцию, которая упрощается при дифференцировании.
обычно выбирают функцию, которая упрощается при дифференцировании.
Некоторые стандартные случаи функций, интегрируемых по частям, указаны в таблице 1. Там же дается способ выбора множителей 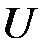 и
и 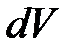 .
.
Таблица 1
| Вид интеграла | 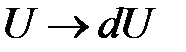
| 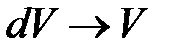
|
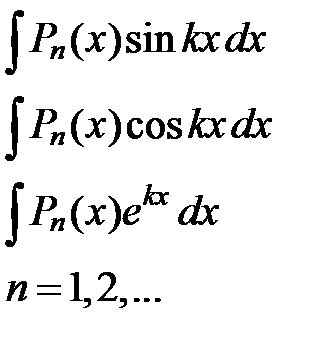
| 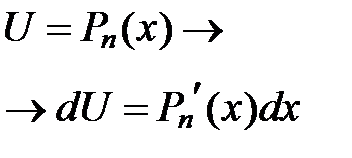
| 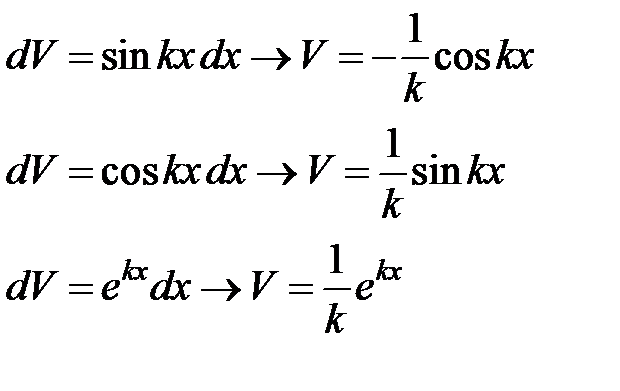
|
| Вид интеграла | 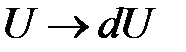
| 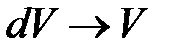
|
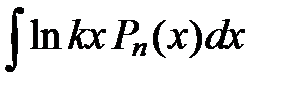
| 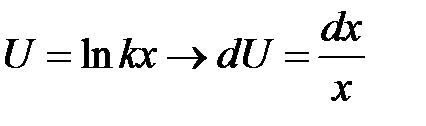
|
|
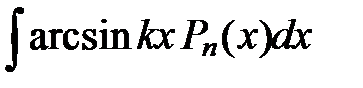
| 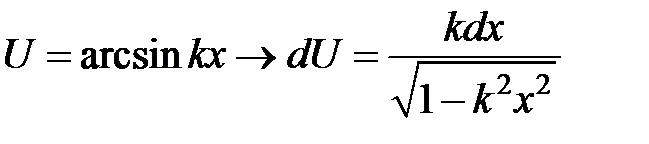
| |
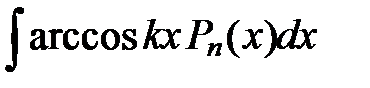
| 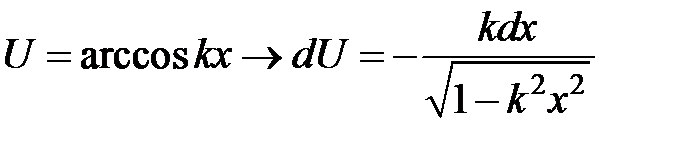
| |
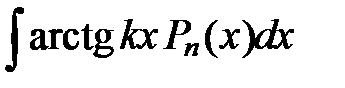
| 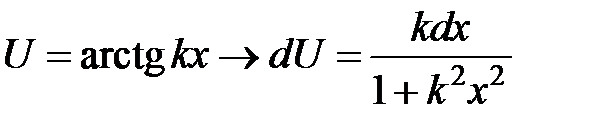
| |
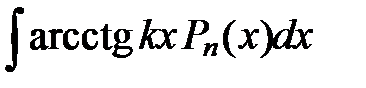
| 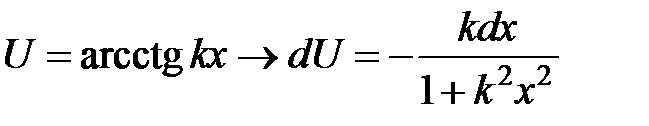
| |
|
| ||
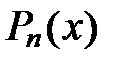 — многочлен от
— многочлен от 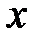 степени
степени 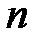 , т. е.
, т. е. 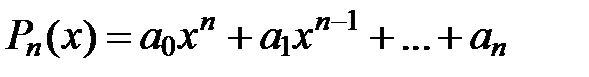 , где
, где 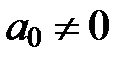 .
.
Пример 3. Проинтегрировать по частям.
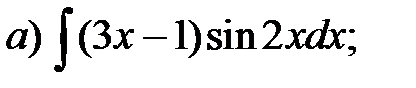
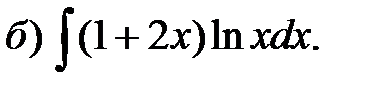
Решение.
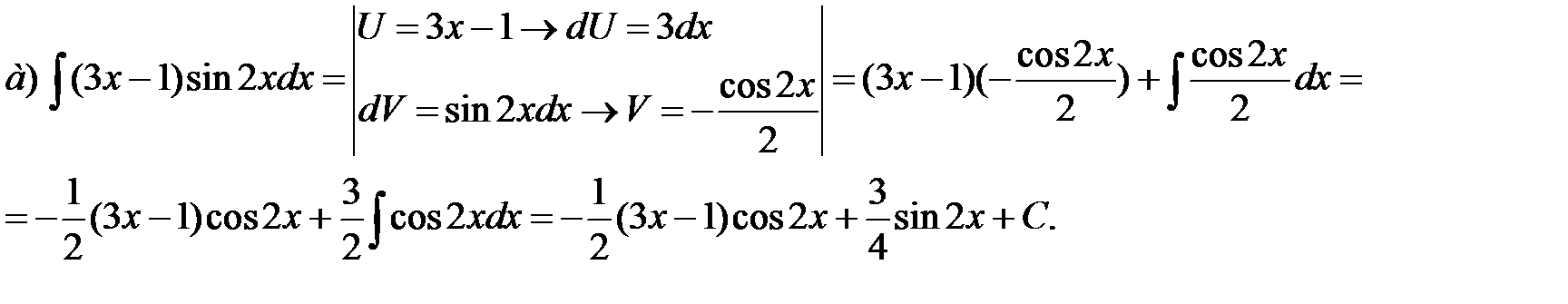
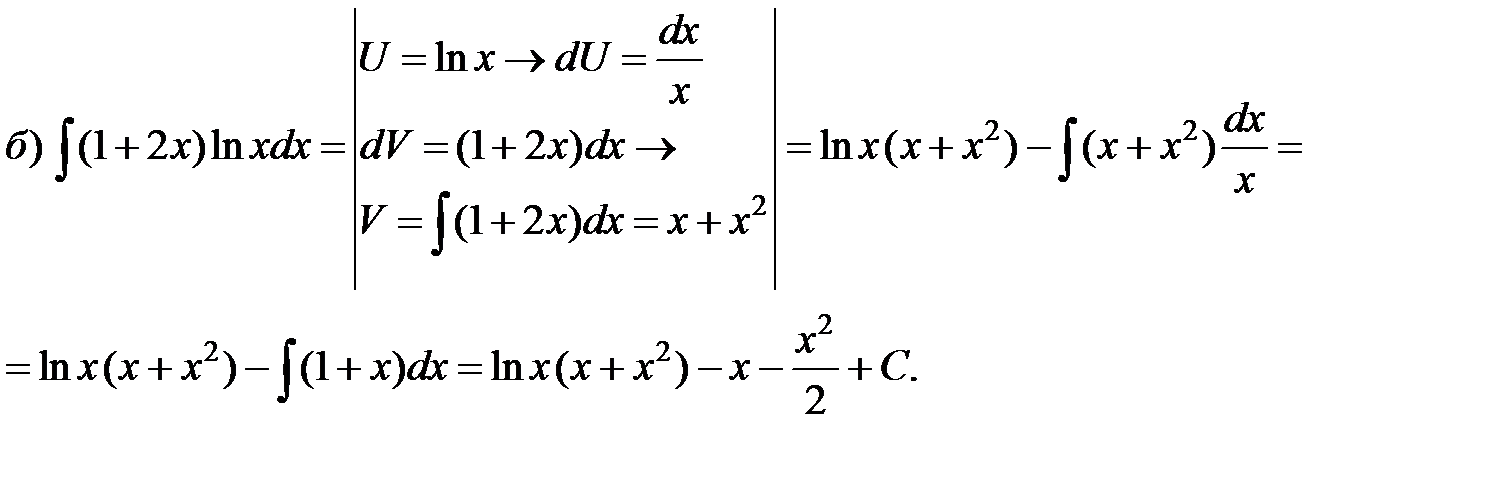
Дата: 2019-04-23, просмотров: 437.