Предел функции f(x) при х®а, где а- число, равен бесконечности, если для любого числа М>0 существует такое число D>0, что неравенство
ïf(x)ï>M
выполняется при всех х, удовлетворяющих условию
0 < ïx - aï < D
Записывается 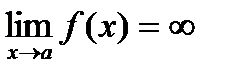 .
.
Собственно, если в приведенном выше определении заменить условие ïf(x)ï>M на f(x)>M, то получим:
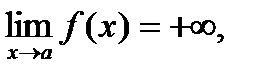
а если заменить на f(x)<M, то:
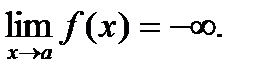
Графически приведенные выше случаи можно проиллюстрировать следующим образом:
a x a x a x
Функция называется бесконечно большой при х®а, где а – чосли или одна из величин ¥, +¥ или -¥, если 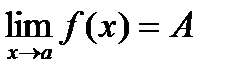 , где А – число или одна из величин ¥, +¥ или -¥.
, где А – число или одна из величин ¥, +¥ или -¥.
Связь бесконечно больших и бесконечно малых функций осуществляется в соответствии со следующей теоремой.
Теорема. Если f ( x ) ® 0 при х ® а (если х ® ¥ ) и не обращается в ноль, то 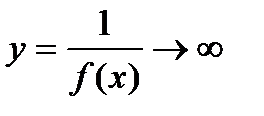
1. Найти 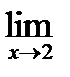 (
( 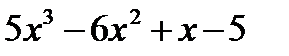 )
)
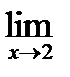 (
( 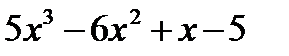 )=13
)=13
Используем теорему о пределе суммы, произведения и следствия о пределе степени
2. Найти 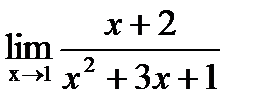 .
.
Так как пределы числителя и знаменателя существуют и предел знаменателя не равен нулю, то можно применить теорему о пределе дроби:
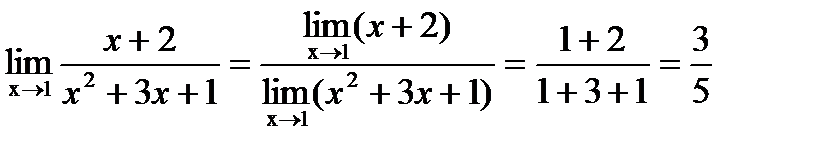 .
.
3. Найти 
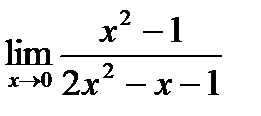
Решение.
Так как пределы числителя и знаменателя существуют и предел знаменателя не равен нулю, то можно применить теорему о пределе дроби:
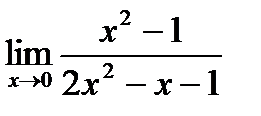 =
= 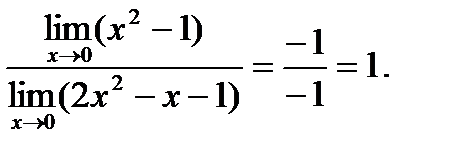
4. Найти 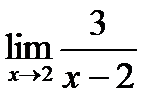
Решение.
Так как предел знаменателя при 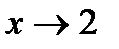 равен 0, тогда знаменатель бесконечно малая функция , следовательно
равен 0, тогда знаменатель бесконечно малая функция , следовательно
функция обратная ей является функцией бесконечно большой, предел которой равен 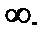
5. Найти 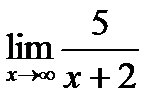
Решение.
Так как предел знаменателя при 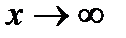 равен
равен 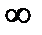 , тогда знаменатель бесконечно большая функция , следовательно
, тогда знаменатель бесконечно большая функция , следовательно
функция обратная ей является функцией бесконечно малой , предел которой равен 0.
Раскрытие неопределенностей вида 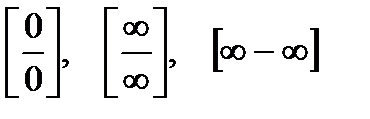
1. Найти предел 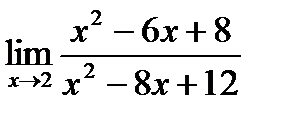 .
.
Для нахождения этого предела разложим на множители числитель и знаменатель данной дроби.
x 2 – 6 x + 8 = 0; x 2 – 8 x + 12 = 0;
D = 36 – 32 = 4; D = 64 – 48 = 16;
x 1 = (6 + 2)/2 = 4; x 1 = (8 + 4)/2 = 6;
x 2 = (6 – 2)/2 = 2 ; x 2 = (8 – 4)/2 = 2;
Тогда 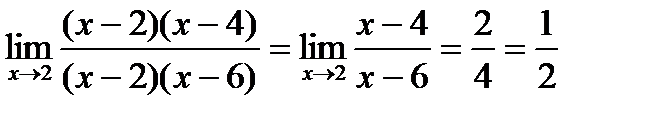
2. Найти предел 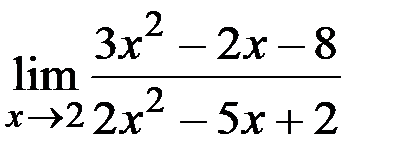 .
.
Теорему о пределе элементарной функции здесь применить нельзя, так как в точке 2 знаменатель рассматриваемой дроби обращается в нуль. Имеем неопределенность вида 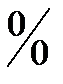 .
.
Разложим числитель и знаменатель на множители. Получим
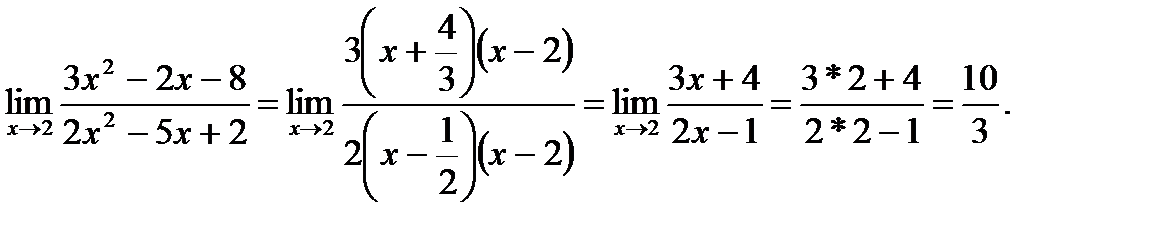
Ответ: 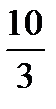 .
.
3. Найти предел 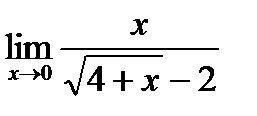 .
.
При х→0 числитель и знаменатель дроби стремится к нулю, т.е. имеем неопределенность вида 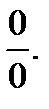 Чтобы раскрыть эту неопределенность, избавимся от иррациональности в знаменателе, умножив числитель и знаменатель дроби на
Чтобы раскрыть эту неопределенность, избавимся от иррациональности в знаменателе, умножив числитель и знаменатель дроби на 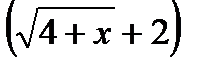 .
.
Таким образом,
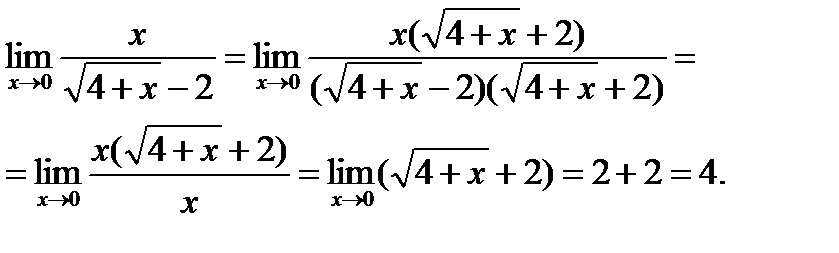
Ответ: 4.
4. Найти предел 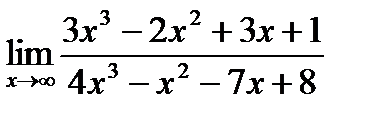 .
.
При х→∞ числитель и знаменатель дроби стремится к бесконечности, т.е. имеем неопределенность вида 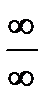 . Чтобы раскрыть эту неопределенность, каждое слагаемое разделим на переменную в самой высокой степени, получим:
. Чтобы раскрыть эту неопределенность, каждое слагаемое разделим на переменную в самой высокой степени, получим:
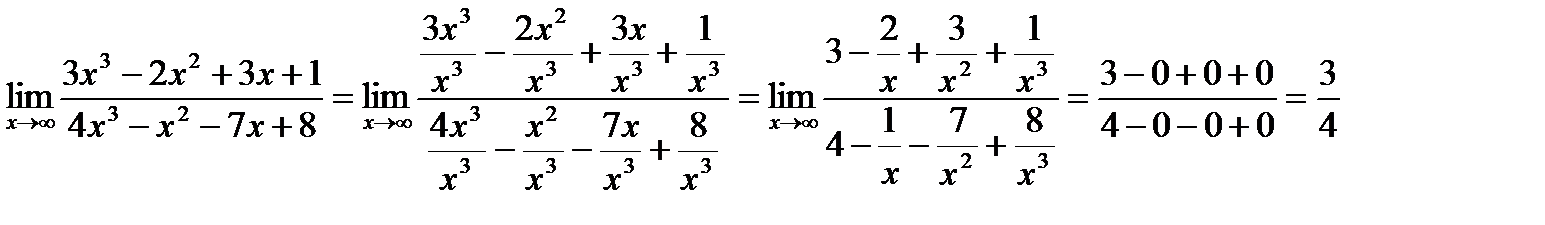
5.Найти предел.
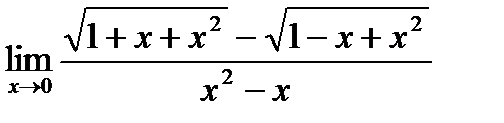 домножим числитель и знаменатель дроби на сопряженное выражение:
домножим числитель и знаменатель дроби на сопряженное выражение: 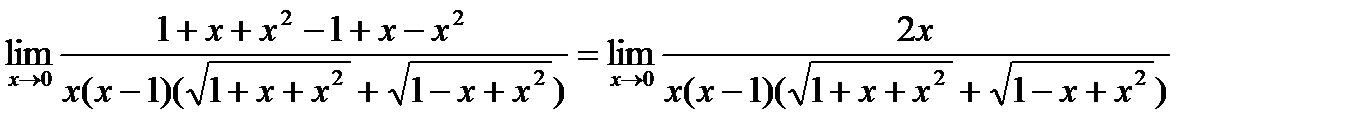 =
=
= 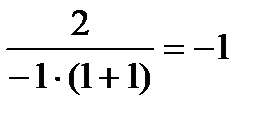 .
.
6. Найти предел 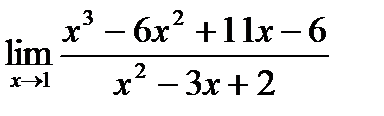 .
.
Разложим числитель и знаменатель на множители.
x 2 – 3 x + 2 = ( x – 1)( x – 2)
x 3 – 6 x 2 + 11 x – 6 = ( x – 1)( x – 2)( x – 3)
Разделим многочлен x 3 – 6 x 2 + 11 x – 6 на х-1
Получим( x – 1)( x – 2)( x – 3),
Тогда 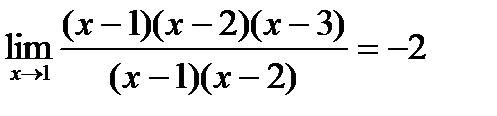
Дата: 2019-04-23, просмотров: 382.