Государственное Бюджетное Профессиональное Образовательное Учреждение
Самарской области
«Самарский политехнический колледж»
МЕТОДИЧЕСКИЕ ПОСОБИЕ
КУРС ЛЕКЦИЙ
по дисциплине «математика»
Для обучающихся заочного отделения
(для всех специальностей)
Самара 2018
Пособие предназначено для оказания помощи студентам заочного отделения при подготовке к экзамену по математике и включает в себя курс лекций.
Пособие может быть использовано студентами дневной формы обучения.
Автор: Кушукова Е.В..- преподаватель Самарского политехнического колледжа
СОДЕРЖАНИЕ
1. Множества.
2. Числовая последовательность и её предел. Предел функции.
3. Производная функции.
4. Неопределенный интеграл. Методы интегрирования.
5. Определенный интеграл
6. Матрицы и определители
7. Мнимая единица. Комплексные числа. Действия над комплексными числами.
8. Размещения, перестановки, сочетания. Классическое определение вероятности.
Тема 1.Множества
Множество – одно из основных понятий математики.
Множеством называется совокупность некоторых элементов, объединенных каким-либо общим признаком. Элементами множества могут быть числа, фигуры, предметы, понятия и т.п.
Множества обозначаются прописными буквами, а элементы множество строчными буквами. Элементы множеств заключаются в фигурные скобки.
Если элемент x принадлежит множеству X, то записывают x ∈ Х (∈ — принадлежит).
Если множество А является частью множества В, то записывают А ⊂ В (⊂ — содержится).
Множество может быть задано одним из двух способов: перечислением и с помощью определяющего свойства.
Два множества А и В равны (А=В), если они состоят из одних и тех же элементов.
Например, если А={1,2,3,4}, B={3,1,4,2} то А=В.
Объединением (суммой) множеств А и В называется множество А ∪ В, элементы которого принадлежат хотя бы одному из этих множеств.
Например, если А={1,2,4}, B={3,4,5,6}, то А ∪ B = {1,2,3,4,5,6}
Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого принадлежат как множеству А, так и множеству В.
Например, если А={1,2,4}, B={3,4,5,2}, то А ∩ В = {2,4}
Разностью множеств А и В называется множество АВ, элементы которого принадлежат множесву А, но не принадлежат множеству В.
Например, если А={1,2,3,4}, B={3,4,5}, то АВ = {1,2}
Симметричной разностью множеств А и В называется множество А Δ В, являющееся объединением разностей множеств АВ и ВА, то есть А Δ В = (АВ) ∪ (ВА).
Например, если А={1,2,3,4}, B={3,4,5,6}, то А Δ В = {1,2} ∪ {5,6} = {1,2,5,6}
Свойства:
Свойства перестановочности:
A ∪ B = B ∪ A
A ∩ B = B ∩ A
Сочетательное свойство:
(A ∪ B) ∪ C = A ∪ (B ∪ C)
(A ∩ B) ∩ C = A ∩ (B ∩ C)
Круги Эйлера (Эйлера-Вена) — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления.
Пример: Среди школьников шестого класса проводилось анкетирование по любимым мультфильмам. Самыми популярными оказались три мультфильма: «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны», «Волк и теленок». Всего в классе 38 человек. «Белоснежку и семь гномов» выбрали 21 ученик, среди которых трое назвали еще «Волк и теленок», шестеро – «Губка Боб Квадратные Штаны», а один написал все три мультфильма. Мультфильм «Волк и теленок» назвали 13 ребят, среди которых пятеро выбрали сразу два мультфильма. Сколько человек выбрали мультфильм «Губка Боб Квадратные Штаны»?
Решение: В этой задаче 3 множества, из условий задачи видно, что все они пересекаются между собой. Получаем такой чертеж:
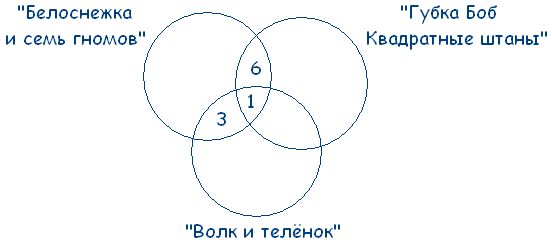
Учитывая условие, что среди ребят, которые назвали мультфильм «Волк и теленок» пятеро выбрали сразу два мультфильма, получаем:
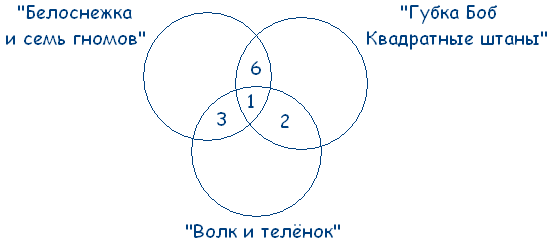
21 – 3 – 6 – 1 = 11 – ребят выбрали только «Белоснежку и семь гномов».
13 – 3 – 1 – 2 = 7 – ребят смотрят только «Волк и теленок».
Получаем:
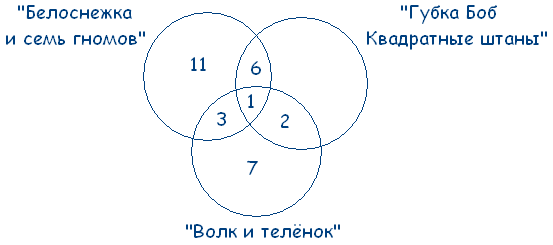
38 – (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят только «Губка Боб Квадратные Штаны».
Делаем вывод, что «Губка Боб Квадратные Штаны» выбрали 8 + 2 + 1 + 6 = 17 человек.
Ответ. 17 человек выбрали мультфильм «Губка Боб Квадратные Штаны».
VII
Функция задана параметричес-кими уравнениями 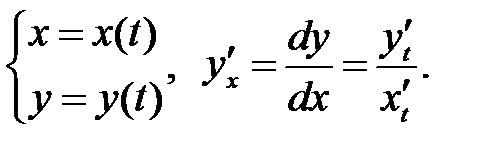
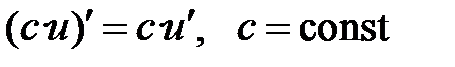
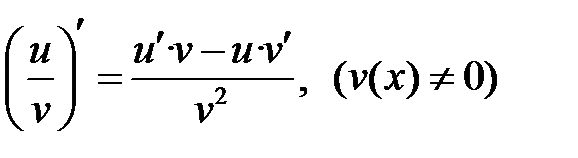
VIII
Если 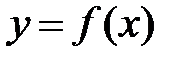 и
и 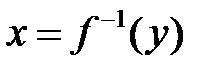 —
—
взаимно обратные функции,
то 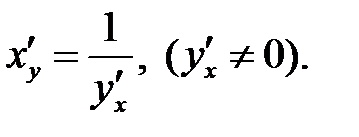
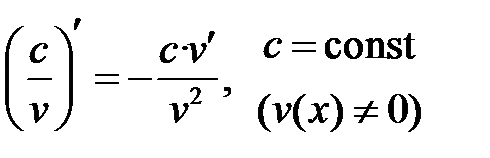
Формулы дифференцирования основных элементарных функций
| № пп | с=const, х — независимая переменная, | ||
| 1 | С’= 0 | 9 | 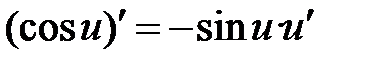
|
| 2 | x’= 1 | 10 | 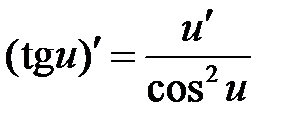
|
| 3 | 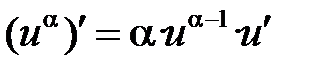
| 11 | 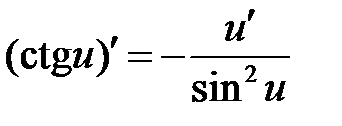
|
| 4 | 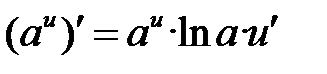
| 12 | 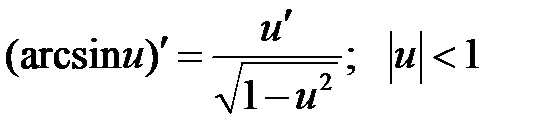
|
| 5 | 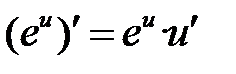
| 13 | 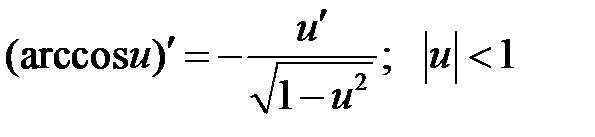
|
| 6 | 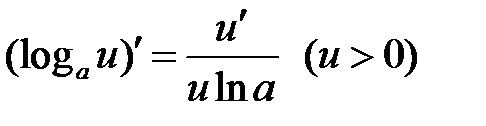
| 14 | 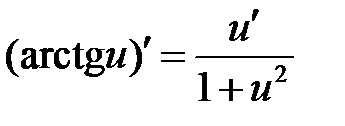
|
| 7 | 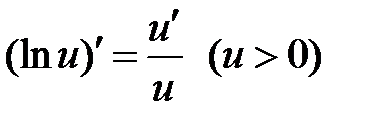
| 15 | 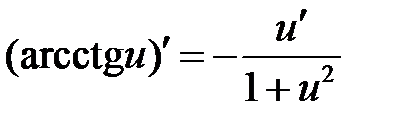
|
| 8 | 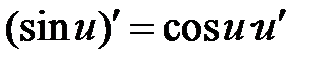
| ||
Производной n-го порядка называется производная от производной (n–1)-го порядка. Производные высших порядков вычисляются последовательным дифференцированием данной функции.
Производная второго порядка 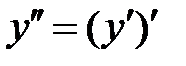 или
или 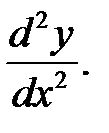
Производная третьего порядка 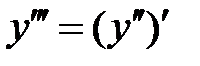 или
или 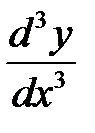 и т. д.
и т. д.
Пример 1. Найти производные функций:
а) 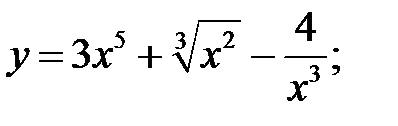 б)
б) 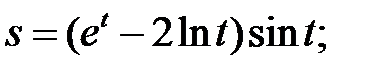 в)
в) 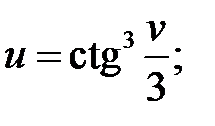 г)
г) 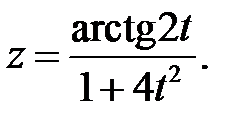
Решение.
а) Используя правила I, III и формулу (3), получим:
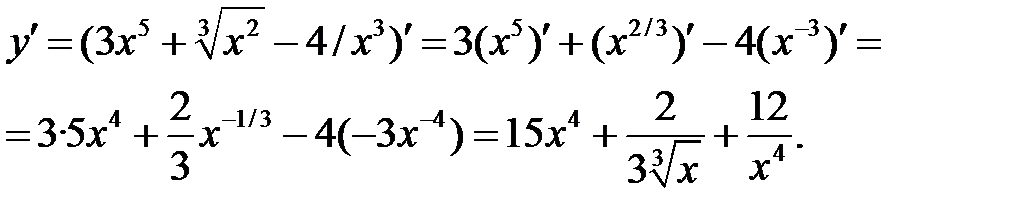
б) Используя правила дифференцирования произведения функций II, разности I, формулы (5), (7), (8) и учитывая, что независимая переменная есть t, т. е. t=1, получим:
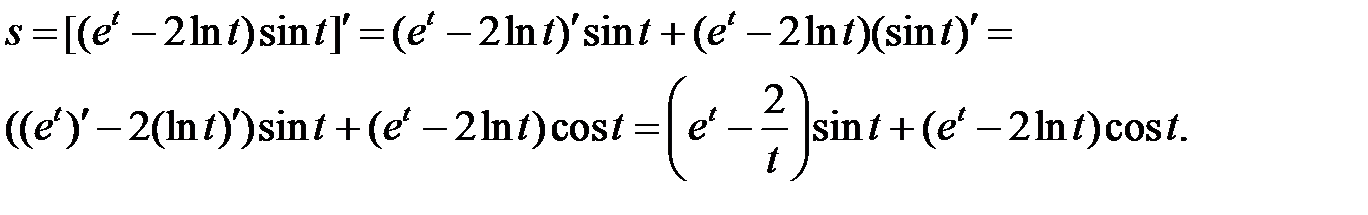
в) Сложная степенная функция, независимая переменная есть v,
т. е. v=1;используя формулу (3), получим: 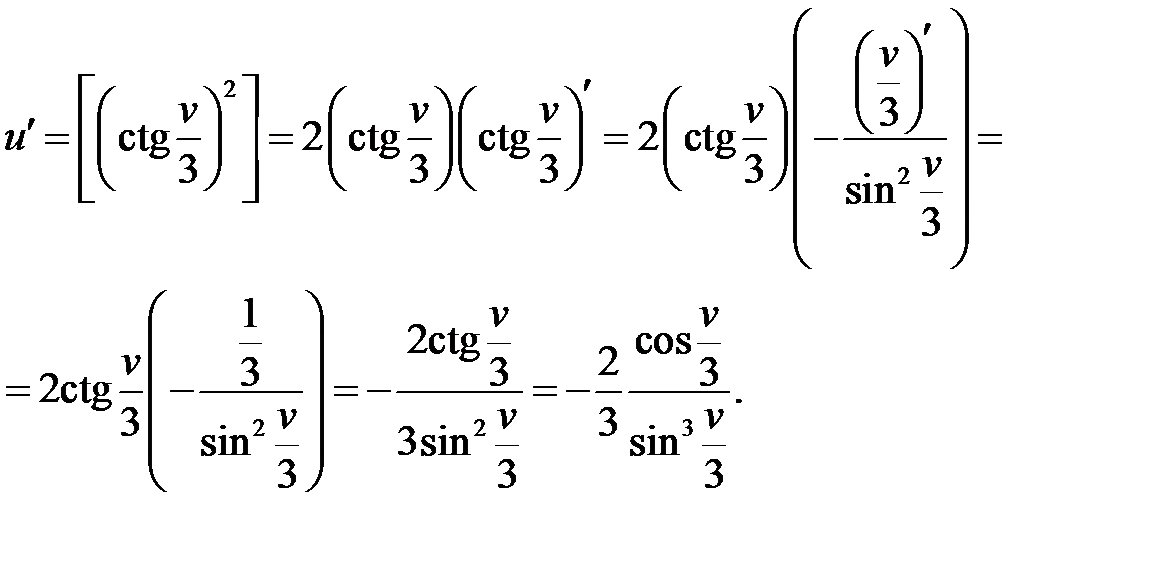
г) Используя правила дифференцирования частного IV, суммы I, III
и формулы (3), (14), учитывая, что t=1, получим:
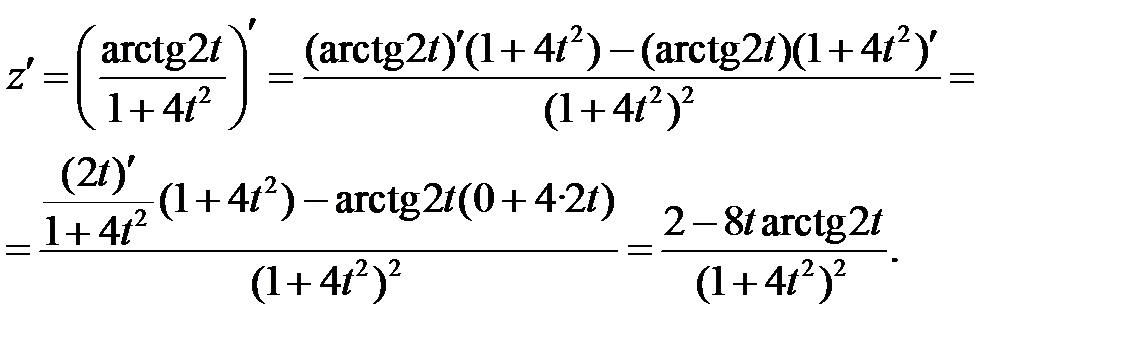
Пример 2. Составить уравнение касательной и нормали к кривой 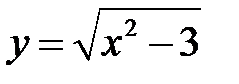 в точке с абсциссой х0=2.
в точке с абсциссой х0=2.
Используем уравнения касательной (2) и нормали (3):
1) 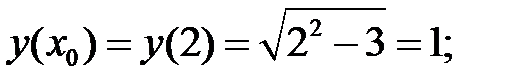
2) 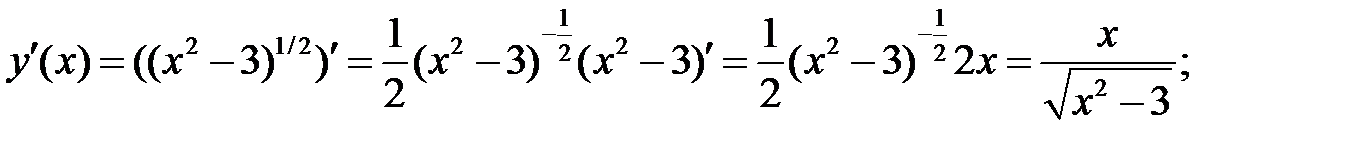
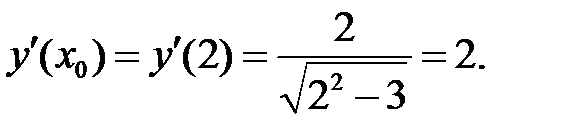
Подставим 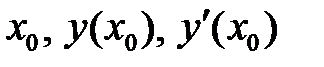 в уравнения и получим:
в уравнения и получим: 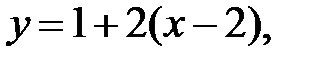
или 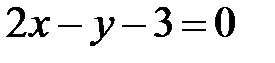 — уравнение касательной.
— уравнение касательной.
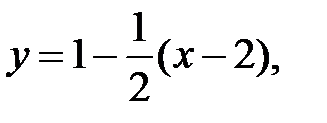 или
или 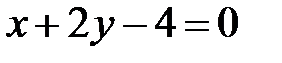 — уравнение нормали.
— уравнение нормали.
Пример 3 . Найти производную 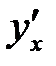 , если функция задана парамет-рически:
, если функция задана парамет-рически: 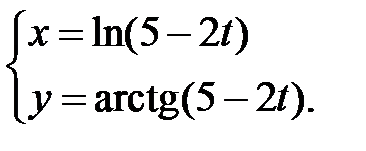
Используем правило VII 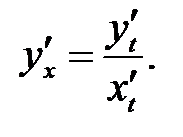
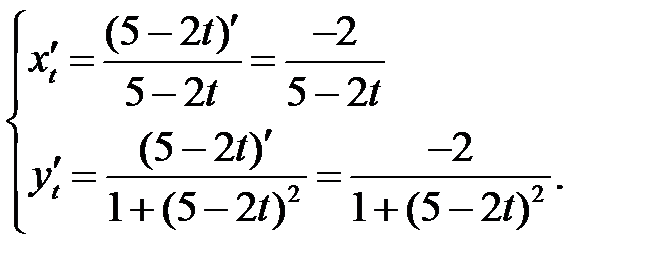
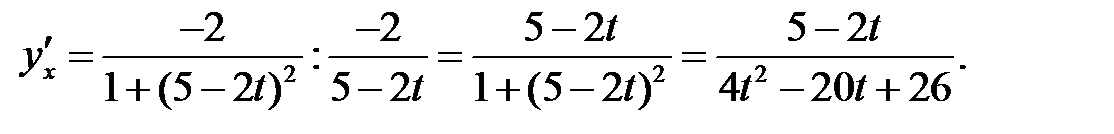
Пример 4. Найти дифференциалы функций:
а) 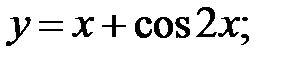 б)
б) 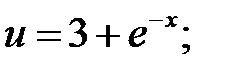 в)
в) 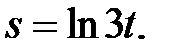
Для дифференциала функции 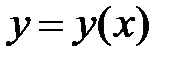 справедлива формула
справедлива формула 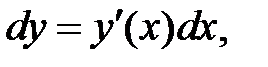 т. е. дифференциал функции равен произведению производной от функции на дифференциал независимой переменной.
т. е. дифференциал функции равен произведению производной от функции на дифференциал независимой переменной.
Решение.
а) 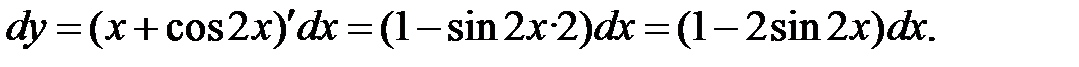
б) 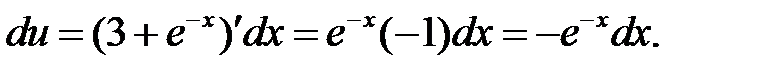
в) 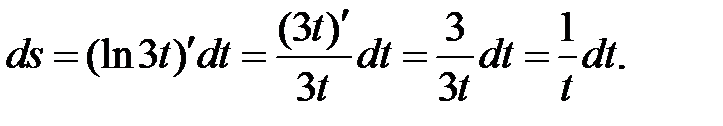
Пример 5 . Найти производную второго порядка функции 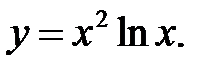
Решение. 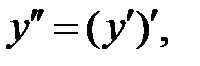 поэтому найдём производную первого порядка,
поэтому найдём производную первого порядка,
а затем второго.
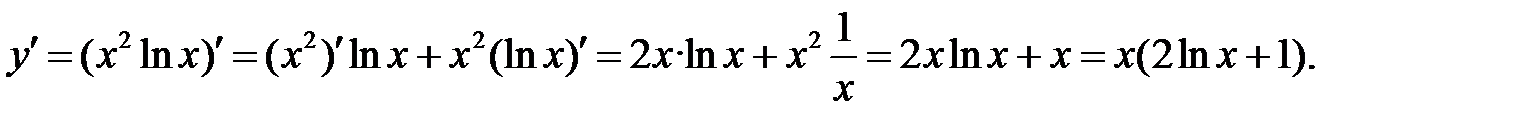
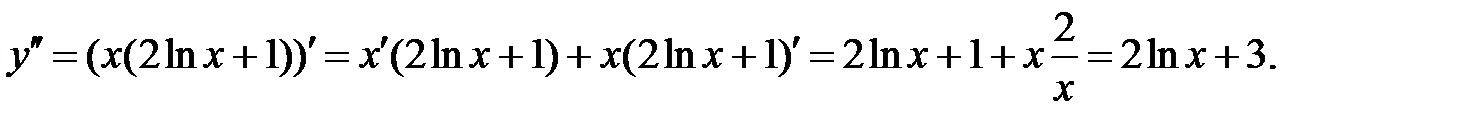
Пример 6. Найти производную функции 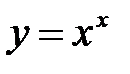 логарифмическим дифференцированием
логарифмическим дифференцированием
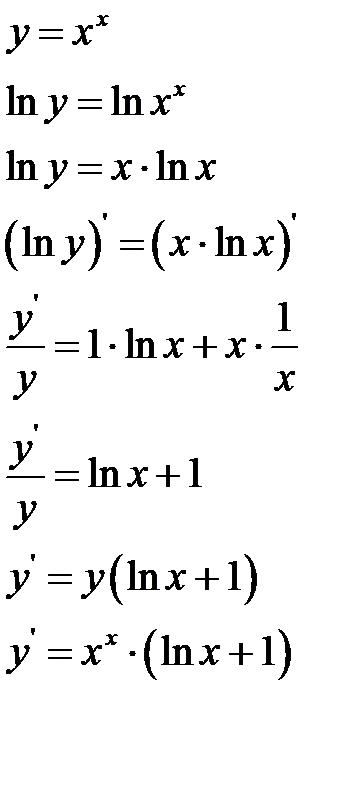
Правило Лопиталя. Предел отношения двух б.м. 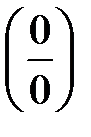 или б.б.
или б.б. 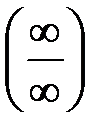 функций равен пределу отношения их производных (конечному или бесконечному), если последний существует:
функций равен пределу отношения их производных (конечному или бесконечному), если последний существует:
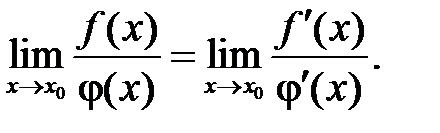 (5)
(5)
Чтобы использовать правило Лопиталя для раскрытия неопределённостей других типов, выражение под знаком предела следует преобразовать элементарными способами так, чтобы получить неопределенность 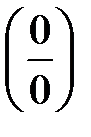 или
или 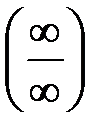 и затем использовать формулу (5).
и затем использовать формулу (5).
Пример 7. Найти пределы, используя правило Лопиталя или элементарные способы раскрытия неопределённостей:
а) 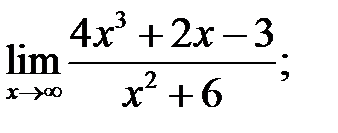 б)
б) 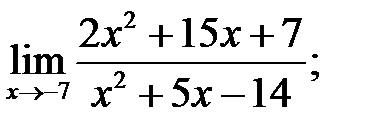
Решение.а) Подставляя в функцию вместо х предельное значение 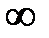 , определим предел числителя и знаменателя.
, определим предел числителя и знаменателя.
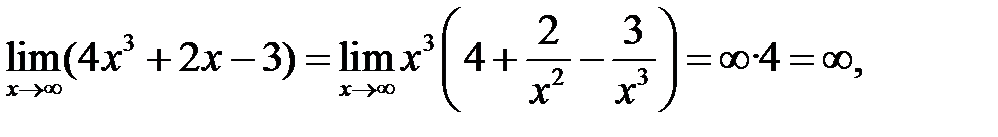 т. к.
т. к. 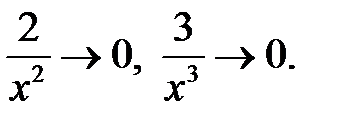
Аналогично: 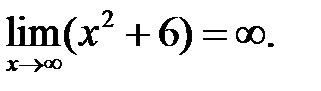 Имеем неопределенность вида
Имеем неопределенность вида 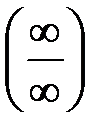 . Используем правило Лопиталя:
. Используем правило Лопиталя:
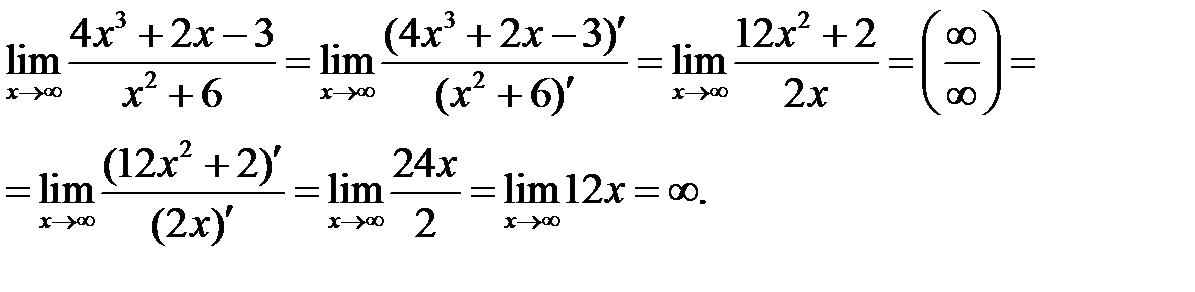
б) 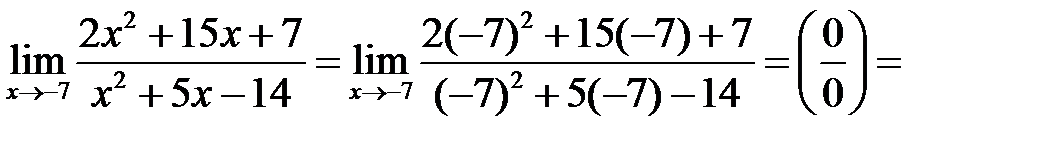
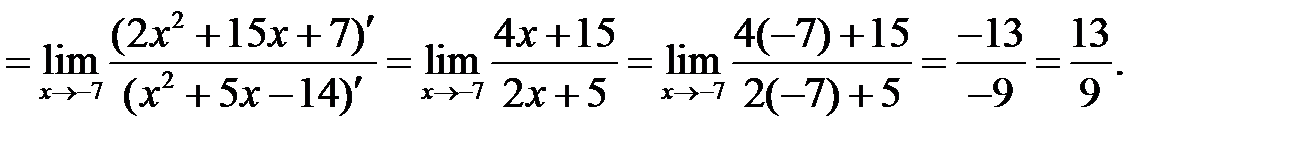
Деление
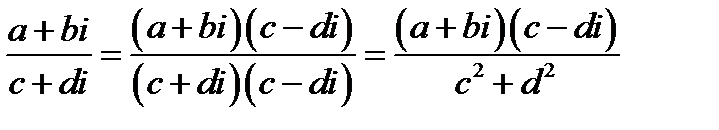
конкретно на примере:
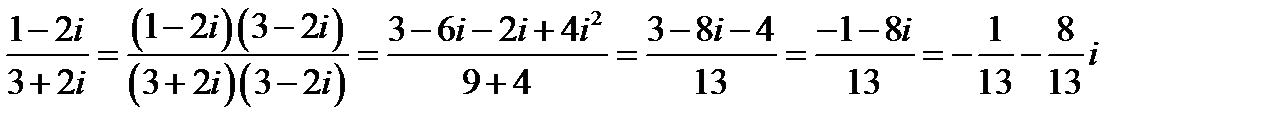
Возведение в квадрат, куб (используем формулы сокращенного умножения)
Z = ( a + b i ) 2 = a 2 + 2 a b i + b 2 i 2 = a 2 + 2 a b i - b 2;
например:
1) ( - 4 + i ) 2 = 16 - 8 i + i 2 = 16 - 8 i - 1 = 15 - 8 i
2) ( 2 - 3 i ) 3 = 8 - 3  22
22  3 i + 3
3 i + 3  2
2  ( - 3 i ) 2 - 27 i 3 = 8 - 36 i + 54 i 2 - 27 i 3 =
( - 3 i ) 2 - 27 i 3 = 8 - 36 i + 54 i 2 - 27 i 3 =
= 8 - 36 i - 54 + 27 i = - 46 - 9 i
Выполнить действия
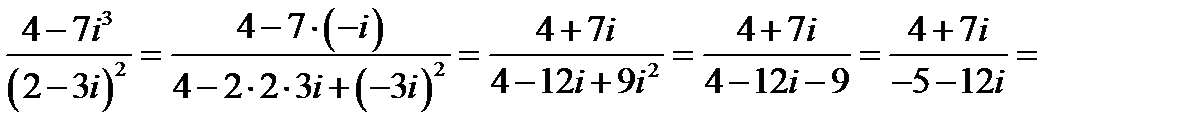
при этих действиях использованы правила: i 3 = - i; i 2 = - 1; ( a - b ) 2 = a 2 - 2 a b + b 2 , а теперь разделим, для этого умножим знаменатель на сопряженное ему число ( - 5 + 12 i) , а чтобы дробь не изменилась умножаем и числитель на это число, т.е.

Тема 8. Размещения, перестановки, сочетания. Классическое определение вероятности.
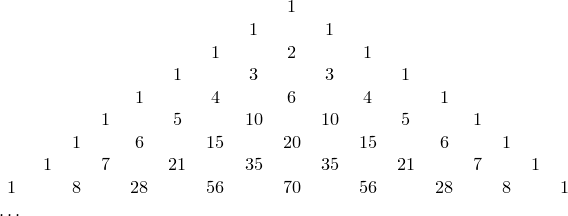
Треугольник Паскаля
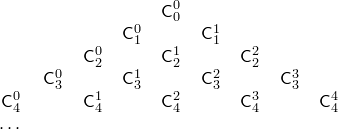
В этом треугольнике крайние числа в каждой строке равны 1, а каждое не крайнее число равно сумме двух чисел предыдущей строки, стоящих над ним. Таким образом, этот треугольник позволяет вычислять числа 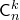 .
.
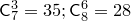 .
.
Теорема. 
Доказательство. Рассмотрим множество из 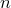 элементов и решим двумя способами следующую задачу: сколько можно составить последовательностей из
элементов и решим двумя способами следующую задачу: сколько можно составить последовательностей из 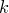 элементов данного
элементов данного
множества, в каждой из которых никакой элемент не встречается дважды?
1 способ. Выбираем первый член последовательности, затем второй, третий и т.д. член
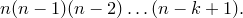
2 способ. Выберем сначала 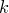 элементов из данного множества, а затем расположим их в некотором порядке
элементов из данного множества, а затем расположим их в некотором порядке
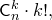
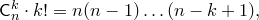
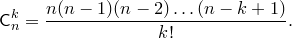
Домножим числитель и знаменатель этой дроби на 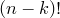 :
:
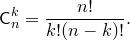
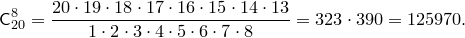
Пример. Сколькими способами можно в игре “Спортлото” выбрать 5 номеров из 36?
Искомое число способов
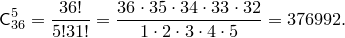
Классическое определение вероятности
Раздел математики, изучающий закономерности случайных событий, называется теорией вероятностей.
Вероятностью Р(А) события А в испытании с равновозможными элементарными исходами называют отношение числа исходов m, благоприятствующих событию А, к числуn всех исходов испытания.
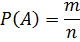
Пример 1: В партии из 30 миксеров 2 бракованных. Найти вероятность купить исправный миксер.
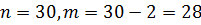
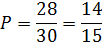
Аксиомы вероятностей:
Каждому событию А поставлено в соответствие неотрицательное число Р(А), называемое вероятностью события А.
Если события А1, А2 … попарно несовместны, то Р(А1+А2+…)=Р(А1)+Р(А2)+…
Свойства вероятностей:
Вероятность невозможного события равна нулю Р=0.
Вероятность достоверного события равна единице Р=1.
Вероятность произвольного случайного события А заключается между 0 и 1: 0<Р(А)<1.
Пример 2: Из 34 экзаменационных билетов, пронумерованных с помощью чисел от 1 до 34, наудачу извлекается один. Какова вероятность, что номер вытянутого билета есть число, кратное трем.
Решение: Найдем количество чисел от 1 до 34, кратных трем. Это числа 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33. Всего таких чисел 11. Таким образом, искомая вероятность 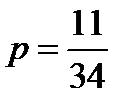
События А и В называются совместными, если они могут одновременно произойти, и несовместными, если при осуществлении одного события не может произойти другое.
События А и В называются независимыми, если вероятность наступления одного события не зависит от того, произошло другое событие или нет.
Вероятность суммы двух совместных событий равна сумме вероятностей слагаемых без вероятности произведения: Р(А+В)=Р(А)+Р(В)-Р(АВ)
Пример 3: Вероятность поражения одной мишени – 0,7, а другой – 0,8. Какова вероятность, что будет поражена хотя бы одна мишень, если по ним стреляют независимо друг от друга.
Решение: Т.к. события совместны, то 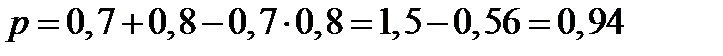
Вероятность суммы двух несовместных событий равна сумме вероятностей слагаемых: Р(А+В)=Р(А)+Р(В).
Р(А)+Р( 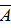 )=1
)=1
Условная вероятность – вероятность одного события, при условии, что другое событие уже произошло.
Вероятность произведения событий А и В равна произведению вероятности одного из них на условную вероятность другого: Р(АВ)=Р(А)∙Р(А/В) или Р(ВА)=Р(А)∙Р(В/А)
Вероятность произведения двух независимых событий А и В равна произведению вероятностей сомножителей: Р(АВ)=Р(А)∙Р(В).
Пример 4: В двух коробках лежат ручки разного цвета. В первой коробке – 4 красных и 6 черных, во второй – 3 красных, 5 синих и 2 черных. Из обеих коробок вынимают по одной ручки. Найти вероятность, что обе ручки красные.
Решение: Найдем вероятности вытащить красную ручку из каждой коробки
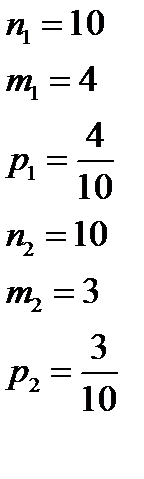
Тогда вероятность того, что обе ручки красные: 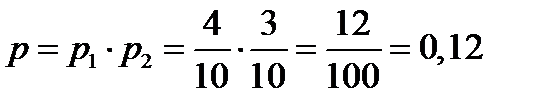
Полная вероятность. Формула Байеса
Если событие А может произойти только при выполнении одного из событий Н1, Н2, …, которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле
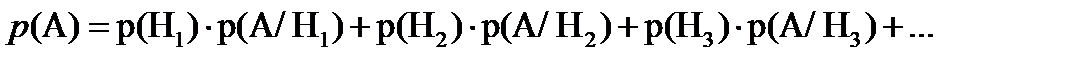
Эта формула называется формулой полной вероятности.
Если выполняются все условия, имеющие место для формулы полной вероятности, и 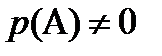 , то выполняется равенство, называемое формулой Байеса:
, то выполняется равенство, называемое формулой Байеса:
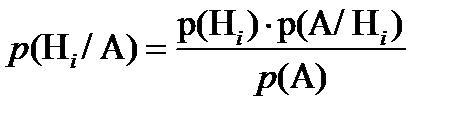
Пример 1: В первой партии 20 ламп, во второй – 30 ламп и в третьей – 50 ламп. Вероятности того, что проработает заданное время, равна для первой партии 0,7, для второй – 0,8 и для третьей партии – 0,9. Какова вероятность того, что наудачу взятая лампа проработает заданное время? Найти вероятность, что эта лампа принадлежит первой партии?
Решение: Пусть событие А – наудачу взятая лампа проработает заданное время.
Тогда, пусть Н1 – лампа из первой партии, Н2 – лампа из второй партии и Н3 – лампа из третьей партии. Тогда событие А/Н1 – лампа из первой партии проработает заданное время, А/Н2 – лампа из второй партии проработает заданное время и А/Н3 – лампа из третьей партии проработает заданное время. Найдем вероятности
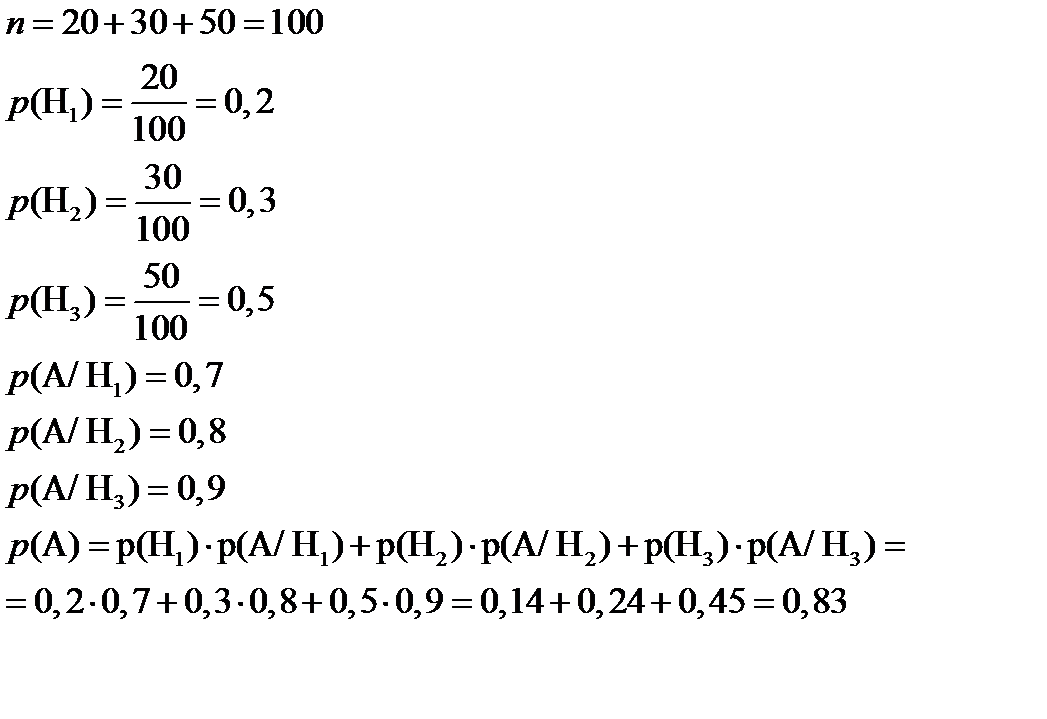
Теперь, используя формулу Байеса найдем вероятность того, что эта лампа принадлежит первой партии
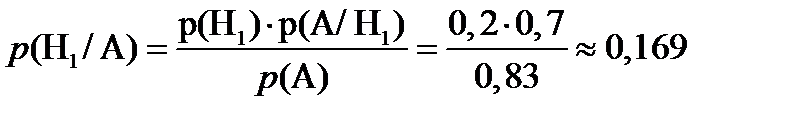
Пример 2: Имеются 3 одинаковые урны. В первой урне находятся 5 белых и 7 черных шаров, во второй – только белые и в третьей – только черные. Наугад выбираются урна и из нее извлекается один шар. Какова вероятность, что этот шар белый?
Решение: Пусть событие А – извлекается белый шар.
Тогда, пусть Н1 – шар из первой урны, Н2 – шар из второй урны и Н3 – шар из третьей урны. Тогда событие А/Н1 – белый шар из первой урны, А/Н2 – белый шар из второй урны и А/Н3 – белый шар из третьей урны. Найдем вероятности
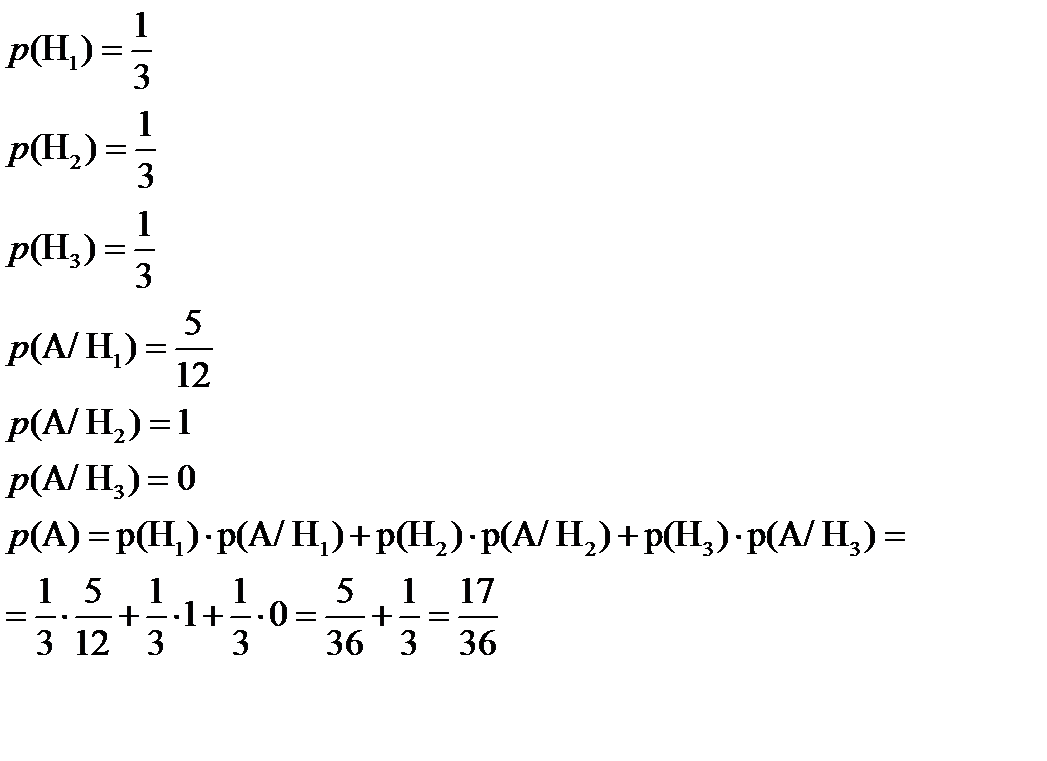
Формула Бернулли
1) Вероятность того, что событие А наступит ровно m раз при проведении n независимых испытаний, каждый из которых имеет ровно два исхода вычисляется по формуле Бернулли 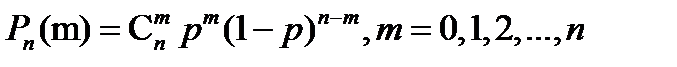
Пример 1: Вероятность выигрыша по одному лотерейному билету равна 0,2. Найти вероятность, что из 6 приобретенных билетов 2 окажутся выигрышными.
Решение:
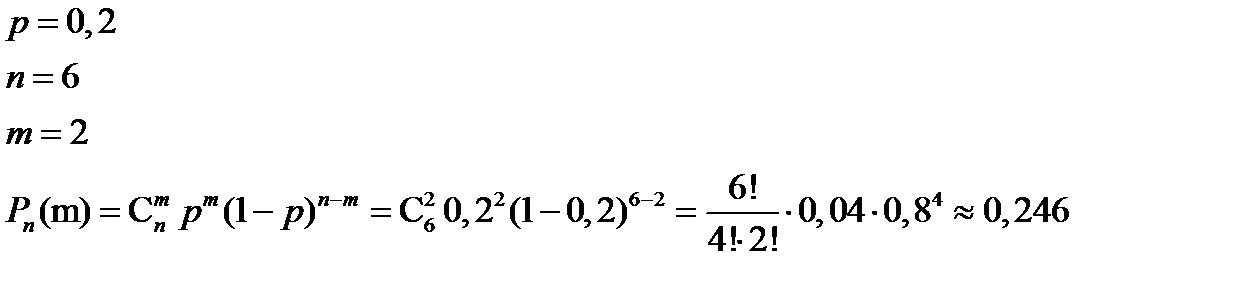
2) Вероятность наступления события А хотя бы один раз при проведении n независимых испытаний, удовлетворяющих схеме Бернулли, равна 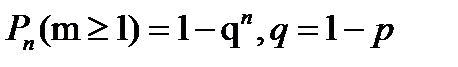
Пример 2: Прибор состоит из шести элементов, работающих независимо друг от друга. Вероятность безотказной работы каждого элемента за определенное время равна 0,6. Для безотказной работы прибора необходимо, чтобы хотя бы один элемент был исправен. Какова вероятность, что за данное время прибор будет работать безотказно?
Решение:
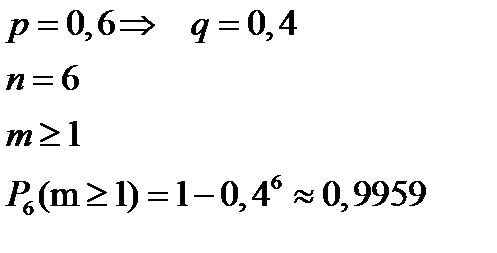
3) Вероятность наступления события А хотя бы один раз при проведении n независимых испытаний, удовлетворяющих схеме Бернулли, наступит не менее m1 и не более m2 раз вычисляется по формуле 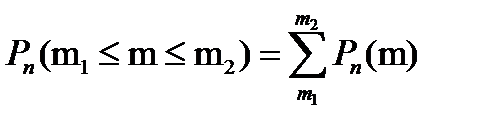
Пример 3: Найти вероятность осуществления от двух до четырех разговоров по телефону при наблюдении пяти независимых вызовов, если вероятность того, что разговор состоится, равна 0,7.
Решение:
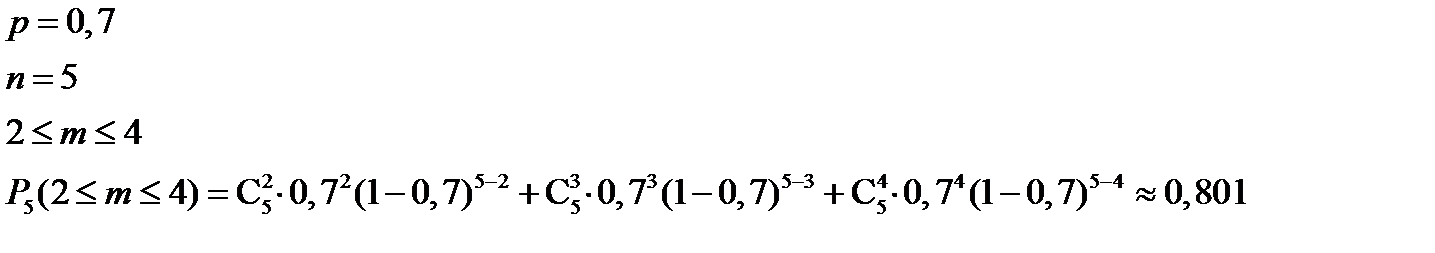
4) Наивероятнейшее значение m0 числа наступления события А при проведении n повторных независимых испытаний, удовлетворяющих схеме Бернулли, вычисляется по формуле 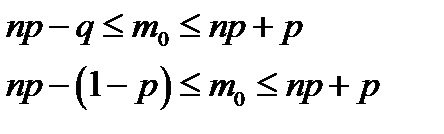
Пример 4: Магазин получил 50 деталей. Вероятность наличия нестандартной детали в партии равна 0,05. Найти наиболее вероятное число нестандартных деталей в партии.
Решение:
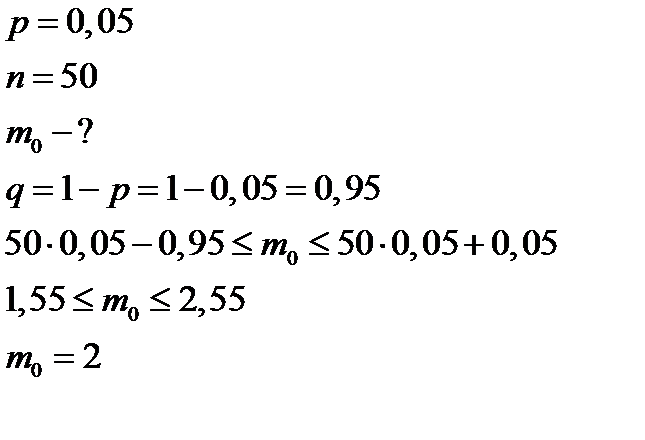
Дискретная случайная величина и ее числовые характеристики
Случайная величина Х – это числовая функция 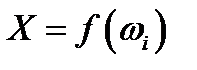 , определенная на пространстве элементарных событий. Случайные величины, имеющие счетные множества возможных значений, называются дискретными. Дискретная случайная величина определена, если известны все ее значения и соответствующие им вероятности. Соотношение между возможными значениями случайной величины и соответствующими им вероятностями называют распределением вероятностей случайной величины. Для дискретной случайной величины это соответствие может быть записано в виде таблицы:
, определенная на пространстве элементарных событий. Случайные величины, имеющие счетные множества возможных значений, называются дискретными. Дискретная случайная величина определена, если известны все ее значения и соответствующие им вероятности. Соотношение между возможными значениями случайной величины и соответствующими им вероятностями называют распределением вероятностей случайной величины. Для дискретной случайной величины это соответствие может быть записано в виде таблицы: 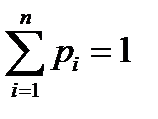
| xi | x1 | x2 | … | xn |
| pi | p1 | p2 | … | pn |
Математическим ожиданием (средним значением) дискретной случайной величины Х называют сумму произведений всех ее возможных значений на соответствующие им вероятности 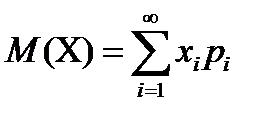
Дисперсией дискретной случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания 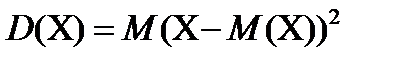 . Дисперсия дискретной случайной величины вычисляется по формулам:
. Дисперсия дискретной случайной величины вычисляется по формулам:
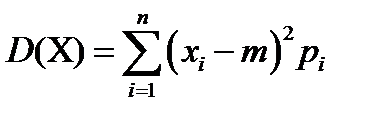
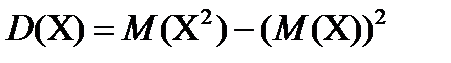
Средним квадратичным отклонением дискретной случайной величины называют корень квадратный из дисперсии 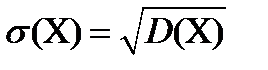 .
.
Если случайная величина Х имеет биномиальное распределение вероятностей, то
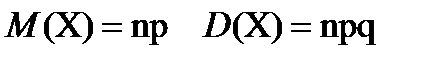
Пример 1: Случайная величина Х задана таблицей распределения вероятностей. Найти М(Х), D(Х), σ(Х).
| хi | 2 | 5 | 8 | 9 |
| рi | 0,1 | 0,4 | 0,3 | 0,2 |
Решение:
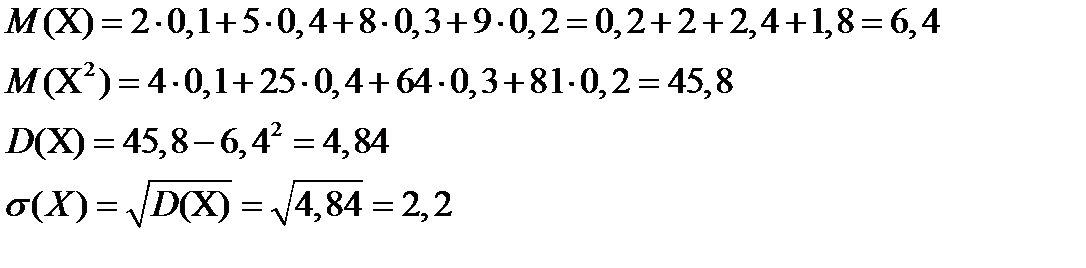
Пример 2: Найти математическое ожидание и дисперсию числа лотерейных билетов, на которые выпадут выигрыши, если приобретено 100 билетов, а вероятность выигрыша на каждый билет равна 0,05.
Решение:
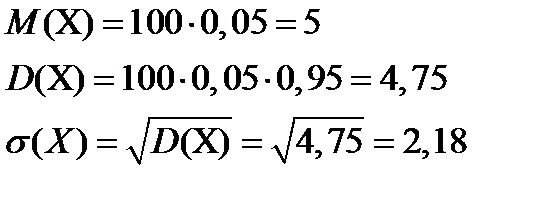
Литература
Основные источники
1. Григорьев С.Г., Иволгина С.В. Математика. – М.: Образовательно-издательский центр «Академия», 2011
2. Григорьев В.П., Сабурова Т.Н. Сборник задач по высшей математике. – М: Издательский центр «Академия», 2011
3. Богомолов Н.В. Практические занятия по математике. – М.: Высшая школа, 2009
4. Дадаян А.А. Математика: учеб.- М.: ФОРУМ: ИНФРА-М, 2005
Дополнительные источники
1. Высшая математика для экономистов. Под ред. Н.Ш. Кремера. – М.: ЮНИТИ, 2007
2. Математика и информатика: учебник для студ. учреждений сред. проф. образования / Виноградов Ю.Н., Гомола А.И., Потапов В.И., Соколова Е.В./ - М.: Издательский центр «Академия», 2009
3. Математика для профессий и специальностей социально-экономического профиля: учебник для образовательных учреждений нач. и сред. образования / В.А. Гусев, С.Г. Григорьев, С.В. Иволгина. – М.: Издательский центр «Академия», 2011
4. Спирина М.С. дискретная математика: учеб. – М.: Издательский центр «Академия», 2006
5. Омельченко В.П. Математика. – Ростов-на-Дону.: Феникс, 2006
Государственное Бюджетное Профессиональное Образовательное Учреждение
Самарской области
«Самарский политехнический колледж»
МЕТОДИЧЕСКИЕ ПОСОБИЕ
КУРС ЛЕКЦИЙ
по дисциплине «математика»
для обучающихся заочного отделения
(для всех специальностей)
Самара 2018
Пособие предназначено для оказания помощи студентам заочного отделения при подготовке к экзамену по математике и включает в себя курс лекций.
Пособие может быть использовано студентами дневной формы обучения.
Автор: Кушукова Е.В..- преподаватель Самарского политехнического колледжа
СОДЕРЖАНИЕ
1. Множества.
2. Числовая последовательность и её предел. Предел функции.
3. Производная функции.
4. Неопределенный интеграл. Методы интегрирования.
5. Определенный интеграл
6. Матрицы и определители
7. Мнимая единица. Комплексные числа. Действия над комплексными числами.
8. Размещения, перестановки, сочетания. Классическое определение вероятности.
Тема 1.Множества
Множество – одно из основных понятий математики.
Множеством называется совокупность некоторых элементов, объединенных каким-либо общим признаком. Элементами множества могут быть числа, фигуры, предметы, понятия и т.п.
Множества обозначаются прописными буквами, а элементы множество строчными буквами. Элементы множеств заключаются в фигурные скобки.
Если элемент x принадлежит множеству X, то записывают x ∈ Х (∈ — принадлежит).
Если множество А является частью множества В, то записывают А ⊂ В (⊂ — содержится).
Множество может быть задано одним из двух способов: перечислением и с помощью определяющего свойства.
Два множества А и В равны (А=В), если они состоят из одних и тех же элементов.
Например, если А={1,2,3,4}, B={3,1,4,2} то А=В.
Объединением (суммой) множеств А и В называется множество А ∪ В, элементы которого принадлежат хотя бы одному из этих множеств.
Например, если А={1,2,4}, B={3,4,5,6}, то А ∪ B = {1,2,3,4,5,6}
Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого принадлежат как множеству А, так и множеству В.
Например, если А={1,2,4}, B={3,4,5,2}, то А ∩ В = {2,4}
Разностью множеств А и В называется множество АВ, элементы которого принадлежат множесву А, но не принадлежат множеству В.
Например, если А={1,2,3,4}, B={3,4,5}, то АВ = {1,2}
Симметричной разностью множеств А и В называется множество А Δ В, являющееся объединением разностей множеств АВ и ВА, то есть А Δ В = (АВ) ∪ (ВА).
Например, если А={1,2,3,4}, B={3,4,5,6}, то А Δ В = {1,2} ∪ {5,6} = {1,2,5,6}
Свойства:
Свойства перестановочности:
A ∪ B = B ∪ A
A ∩ B = B ∩ A
Сочетательное свойство:
(A ∪ B) ∪ C = A ∪ (B ∪ C)
(A ∩ B) ∩ C = A ∩ (B ∩ C)
Круги Эйлера (Эйлера-Вена) — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления.
Пример: Среди школьников шестого класса проводилось анкетирование по любимым мультфильмам. Самыми популярными оказались три мультфильма: «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны», «Волк и теленок». Всего в классе 38 человек. «Белоснежку и семь гномов» выбрали 21 ученик, среди которых трое назвали еще «Волк и теленок», шестеро – «Губка Боб Квадратные Штаны», а один написал все три мультфильма. Мультфильм «Волк и теленок» назвали 13 ребят, среди которых пятеро выбрали сразу два мультфильма. Сколько человек выбрали мультфильм «Губка Боб Квадратные Штаны»?
Решение: В этой задаче 3 множества, из условий задачи видно, что все они пересекаются между собой. Получаем такой чертеж:

Учитывая условие, что среди ребят, которые назвали мультфильм «Волк и теленок» пятеро выбрали сразу два мультфильма, получаем:

21 – 3 – 6 – 1 = 11 – ребят выбрали только «Белоснежку и семь гномов».
13 – 3 – 1 – 2 = 7 – ребят смотрят только «Волк и теленок».
Получаем:

38 – (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят только «Губка Боб Квадратные Штаны».
Делаем вывод, что «Губка Боб Квадратные Штаны» выбрали 8 + 2 + 1 + 6 = 17 человек.
Ответ. 17 человек выбрали мультфильм «Губка Боб Квадратные Штаны».
Дата: 2019-04-23, просмотров: 434.