Первый замечательный предел. 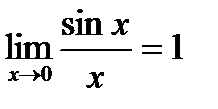
Второй замечательный предел. 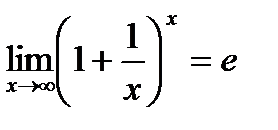
1. Найти 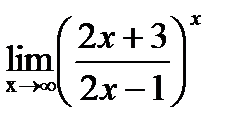 .
.
Здесь имеем неопределенность вида 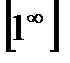 . Для раскрытия этой неопределенности преобразуем функцию так, чтобы можно было воспользоваться вторым замечательным пределом.
. Для раскрытия этой неопределенности преобразуем функцию так, чтобы можно было воспользоваться вторым замечательным пределом.
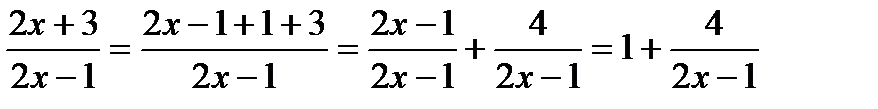 .
.
Введем новую переменную. Пусть 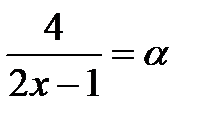 , тогда
, тогда 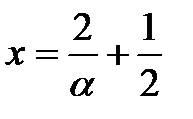 , при
, при 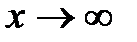 ,
, 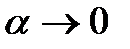 . Следовательно:
. Следовательно:
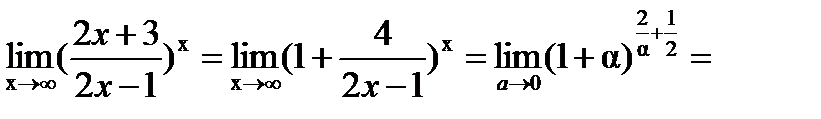
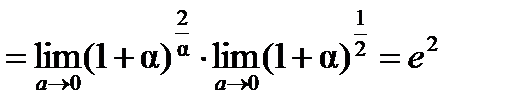
2 .Найти предел.
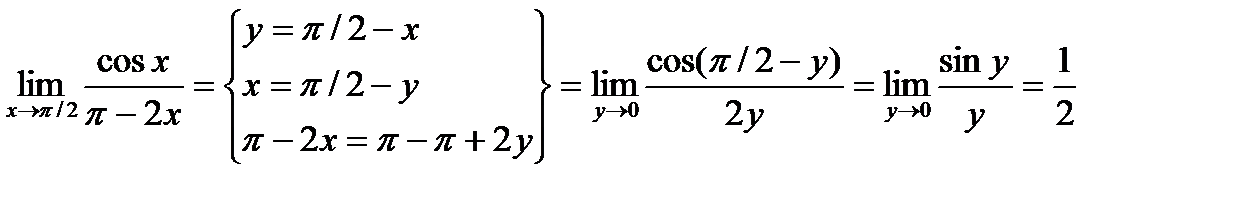
3.Найти предел.
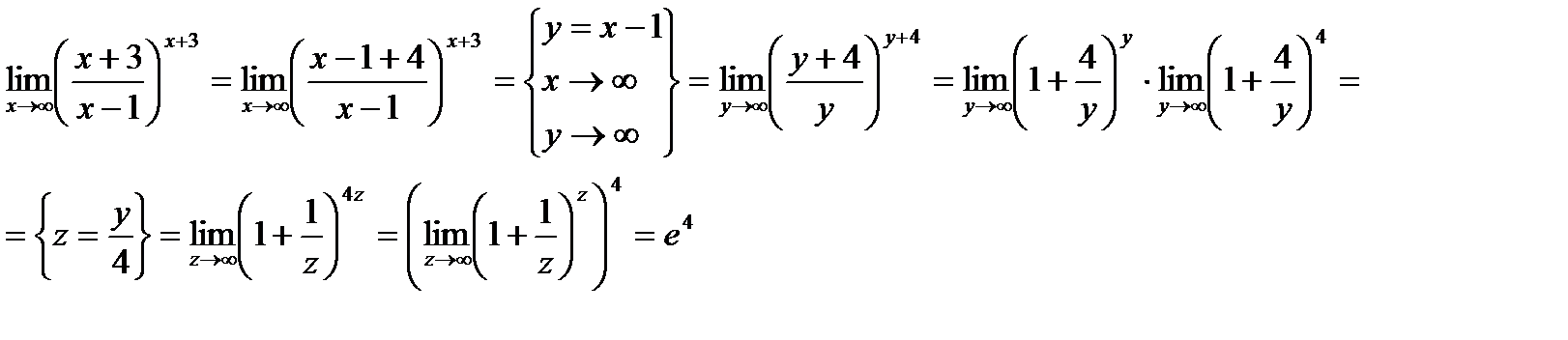
4. Найти  .
.
Имеем: 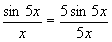 . Обозначим t = 5x. При x0 имеем: t0. Применяя формулу (1), получим
. Обозначим t = 5x. При x0 имеем: t0. Применяя формулу (1), получим  .
.
5. Найти 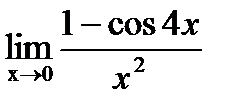 .
.
Имеем неопределенность вида 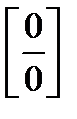 . Воспользуемся первым замечательным пределом.
. Воспользуемся первым замечательным пределом.
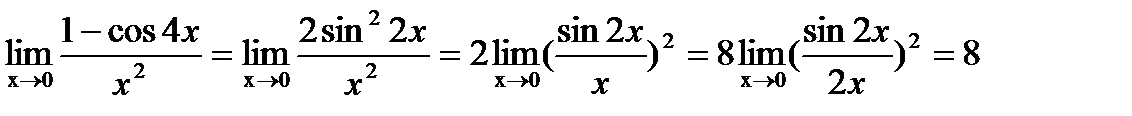 .
.
Можно привести другое решение.
Пусть  , тогда
, тогда 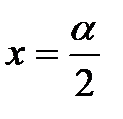 при
при 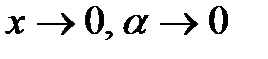 . Тогда
. Тогда
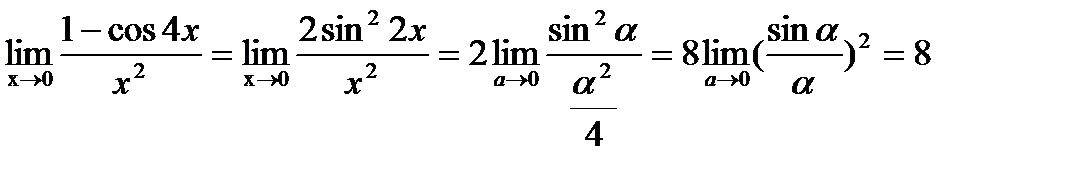 .
.
Тема 3. Производная функции.
Производной функции 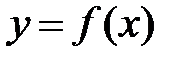 называется конечный предел отношения приращения функции
называется конечный предел отношения приращения функции 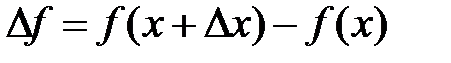 к приращению независимой переменной
к приращению независимой переменной 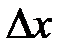 при стремлении последнего к нулю:
при стремлении последнего к нулю:
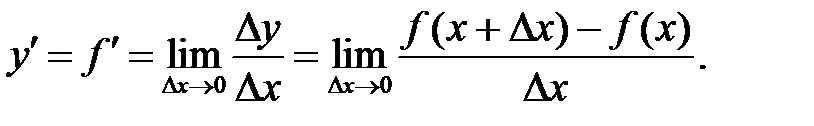 (1)
(1)
Обозначения производной в точке х0:
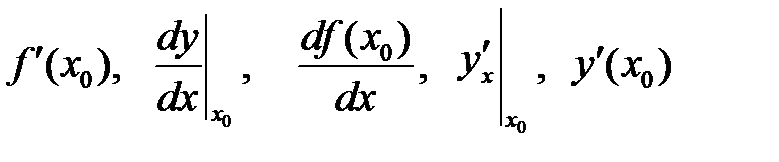 и другие.
и другие.
Если функция в точке х0 (или на промежутке Х) имеет конечную производную, то функция называется дифференцируемой в этой точке (или на промежутке Х).
Процесс отыскания производной называется дифференцированием.

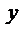
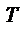
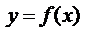
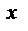
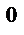
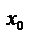
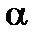
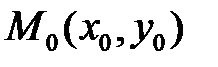
N
Геометрический смысл производной. 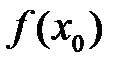
Если кривая задана уравнением 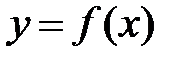 ,
,
то 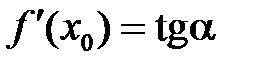 — угловой коэффициент касательной к графику функции в этой точке (
— угловой коэффициент касательной к графику функции в этой точке ( 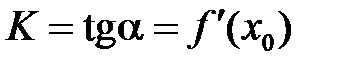 ).
).
Уравнение касательной к кривой 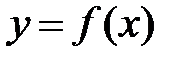
в точке х0 (прямая М0Т) имеет вид:
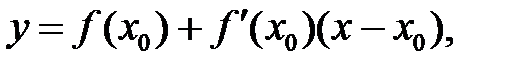 (2)
(2)
а уравнение нормали (М0N):
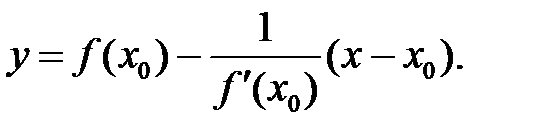 (3)
(3)
Правила дифференцирования
| № пп | U = u(x), V=V(x) — дифференцируемые функции | № пп | U = u(x), V=V(x) — дифференцируемые функции |
| I | 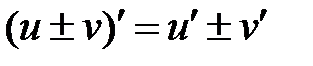
| VI | Производная сложной функции 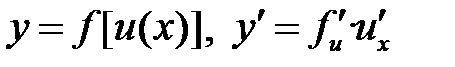
|
| II | 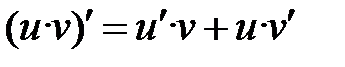
|
VII
Функция задана параметричес-кими уравнениями 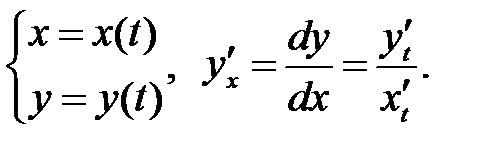
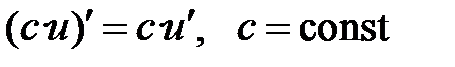
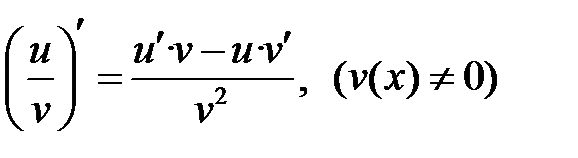
VIII
Если 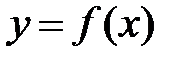 и
и 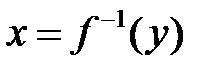 —
—
взаимно обратные функции,
то 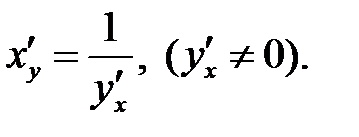
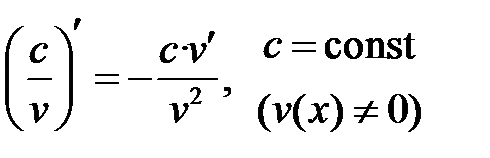
Формулы дифференцирования основных элементарных функций
| № пп | с=const, х — независимая переменная, | ||
| 1 | С’= 0 | 9 | 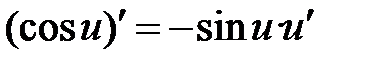
|
| 2 | x’= 1 | 10 | 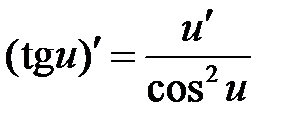
|
| 3 | 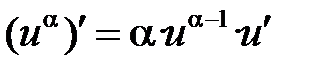
| 11 | 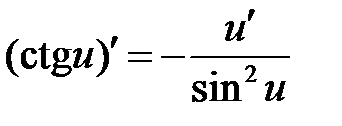
|
| 4 | 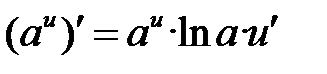
| 12 | 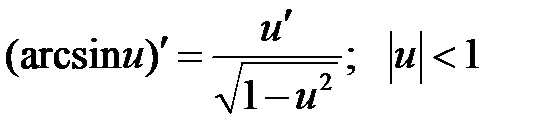
|
| 5 | 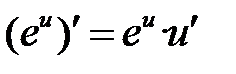
| 13 | 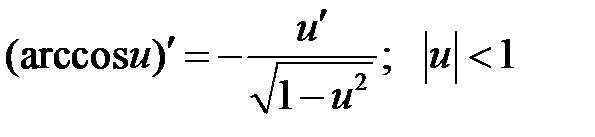
|
| 6 | 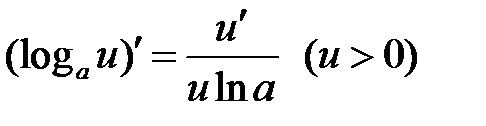
| 14 | 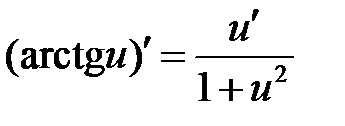
|
| 7 | 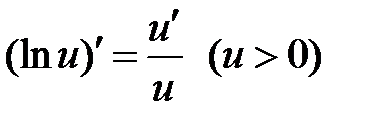
| 15 | 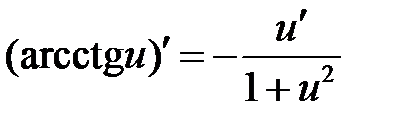
|
| 8 | 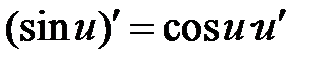
| ||
Производной n-го порядка называется производная от производной (n–1)-го порядка. Производные высших порядков вычисляются последовательным дифференцированием данной функции.
Производная второго порядка 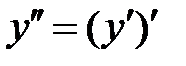 или
или 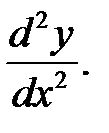
Производная третьего порядка 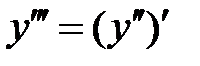 или
или 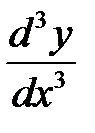 и т. д.
и т. д.
Пример 1. Найти производные функций:
а) 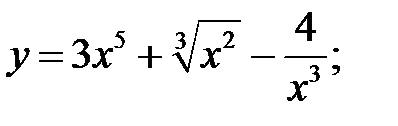 б)
б) 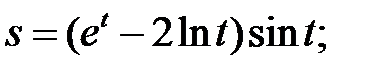 в)
в) 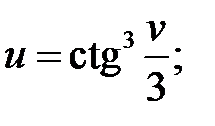 г)
г) 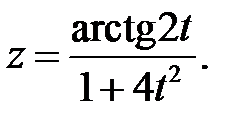
Решение.
а) Используя правила I, III и формулу (3), получим:
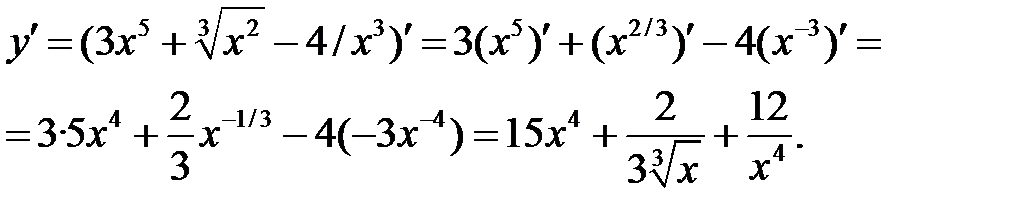
б) Используя правила дифференцирования произведения функций II, разности I, формулы (5), (7), (8) и учитывая, что независимая переменная есть t, т. е. t=1, получим:
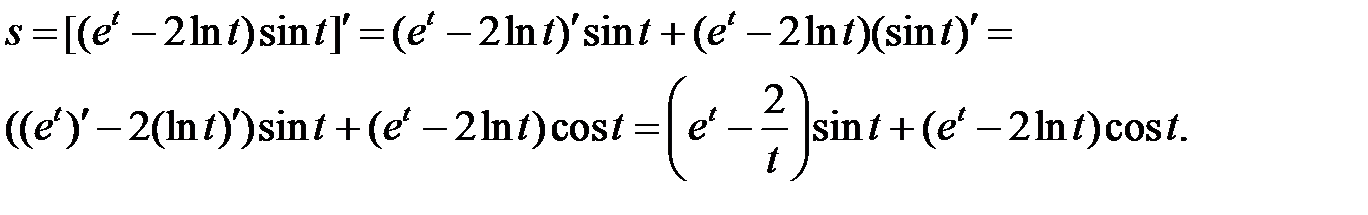
в) Сложная степенная функция, независимая переменная есть v,
т. е. v=1;используя формулу (3), получим: 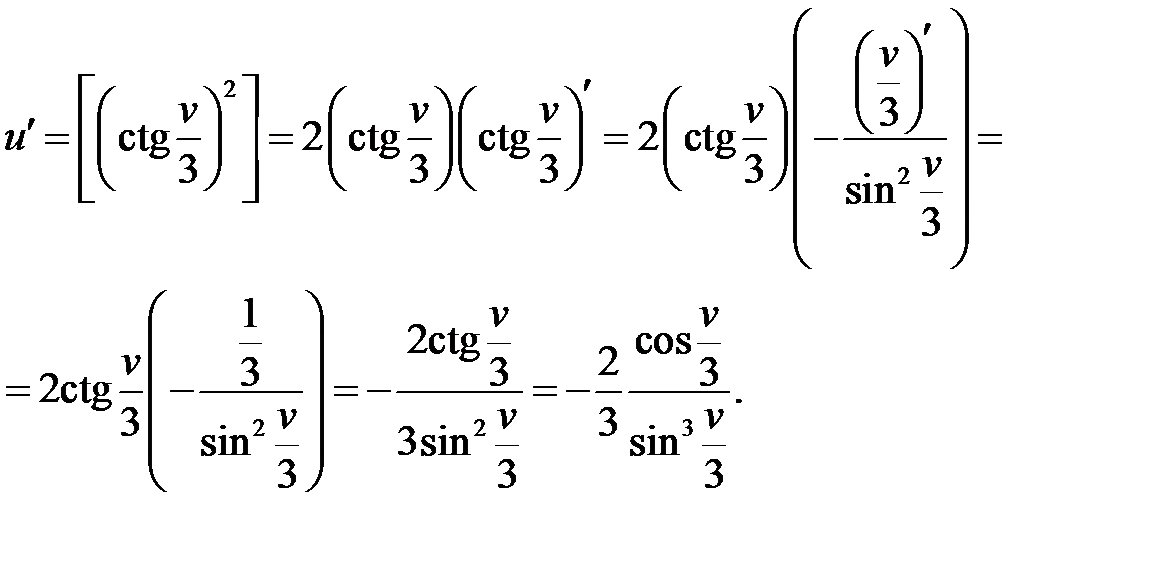
г) Используя правила дифференцирования частного IV, суммы I, III
и формулы (3), (14), учитывая, что t=1, получим:
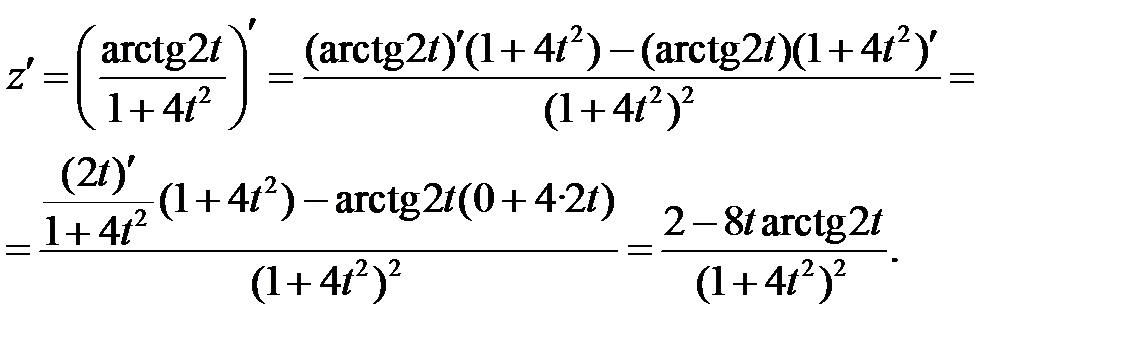
Пример 2. Составить уравнение касательной и нормали к кривой 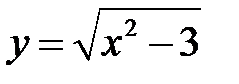 в точке с абсциссой х0=2.
в точке с абсциссой х0=2.
Используем уравнения касательной (2) и нормали (3):
1) 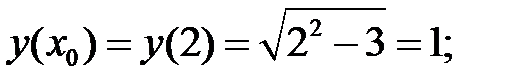
2) 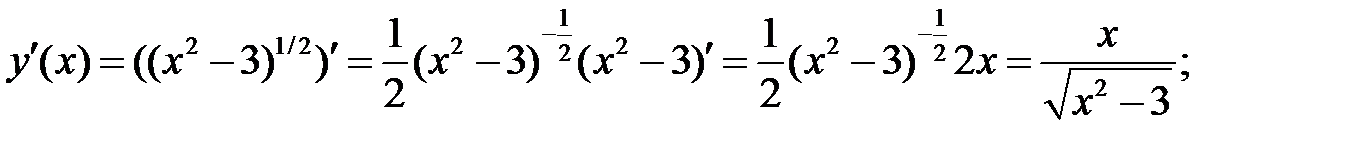
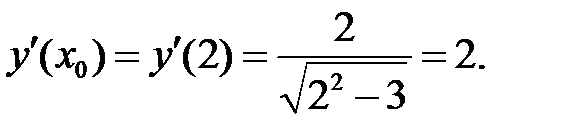
Подставим 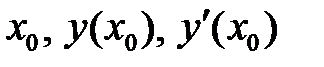 в уравнения и получим:
в уравнения и получим: 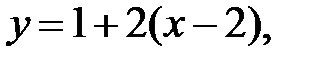
или 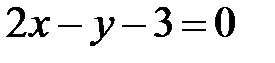 — уравнение касательной.
— уравнение касательной.
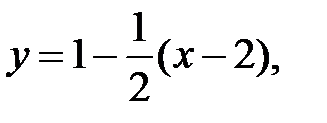 или
или 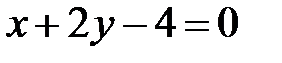 — уравнение нормали.
— уравнение нормали.
Пример 3 . Найти производную 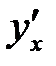 , если функция задана парамет-рически:
, если функция задана парамет-рически: 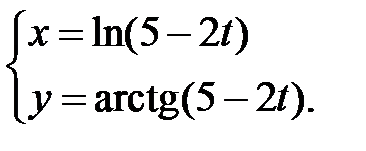
Используем правило VII 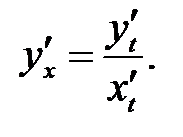
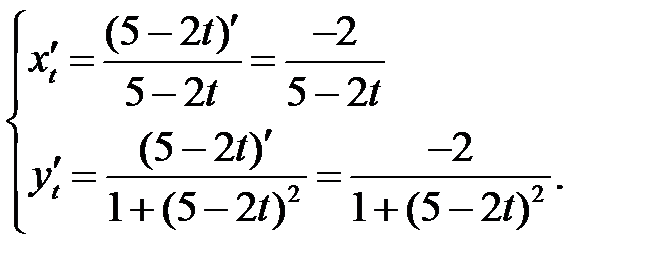
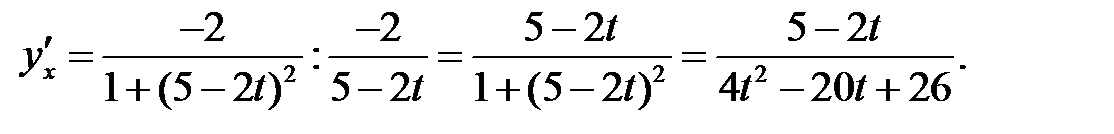
Пример 4. Найти дифференциалы функций:
а) 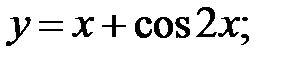 б)
б) 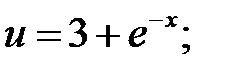 в)
в) 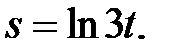
Для дифференциала функции 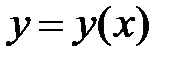 справедлива формула
справедлива формула 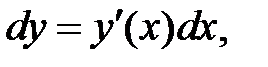 т. е. дифференциал функции равен произведению производной от функции на дифференциал независимой переменной.
т. е. дифференциал функции равен произведению производной от функции на дифференциал независимой переменной.
Решение.
а) 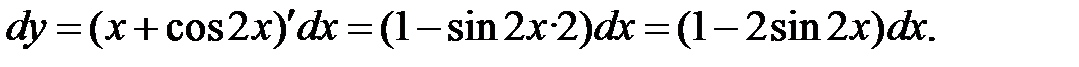
б) 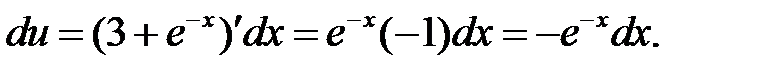
в) 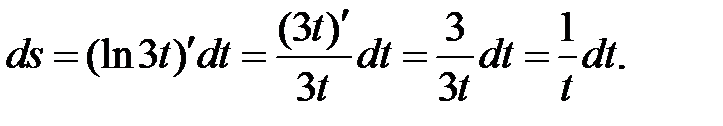
Пример 5 . Найти производную второго порядка функции 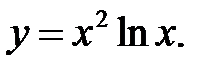
Решение. 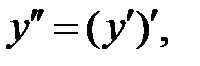 поэтому найдём производную первого порядка,
поэтому найдём производную первого порядка,
а затем второго.
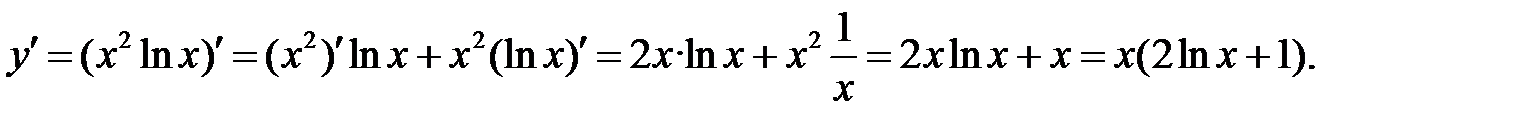
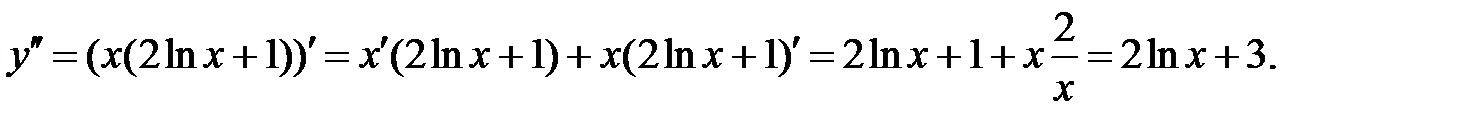
Пример 6. Найти производную функции 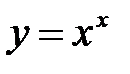 логарифмическим дифференцированием
логарифмическим дифференцированием
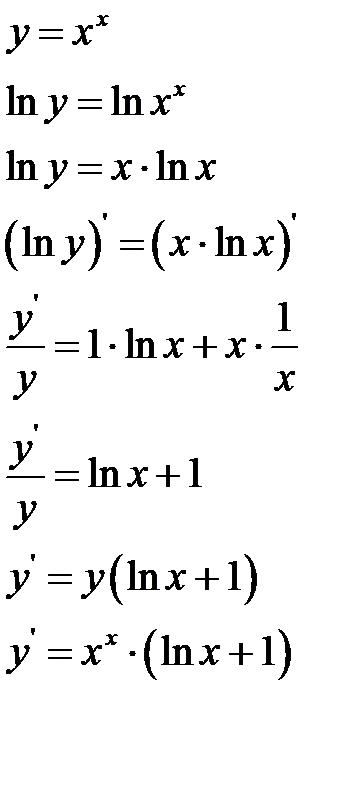
Правило Лопиталя. Предел отношения двух б.м. 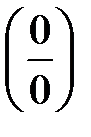 или б.б.
или б.б. 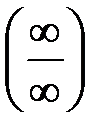 функций равен пределу отношения их производных (конечному или бесконечному), если последний существует:
функций равен пределу отношения их производных (конечному или бесконечному), если последний существует:
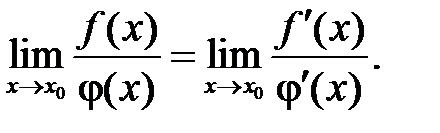 (5)
(5)
Чтобы использовать правило Лопиталя для раскрытия неопределённостей других типов, выражение под знаком предела следует преобразовать элементарными способами так, чтобы получить неопределенность 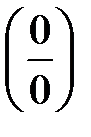 или
или 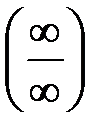 и затем использовать формулу (5).
и затем использовать формулу (5).
Пример 7. Найти пределы, используя правило Лопиталя или элементарные способы раскрытия неопределённостей:
а) 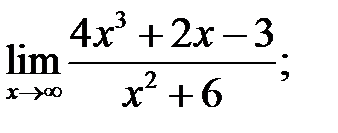 б)
б) 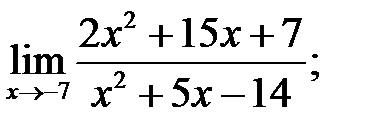
Решение.а) Подставляя в функцию вместо х предельное значение 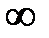 , определим предел числителя и знаменателя.
, определим предел числителя и знаменателя.
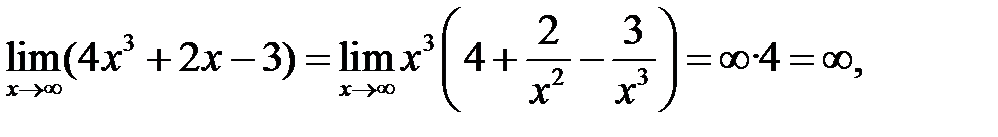 т. к.
т. к. 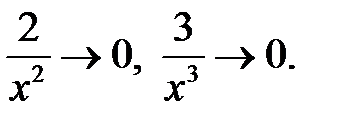
Аналогично: 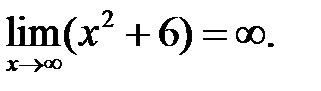 Имеем неопределенность вида
Имеем неопределенность вида 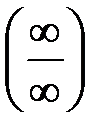 . Используем правило Лопиталя:
. Используем правило Лопиталя:
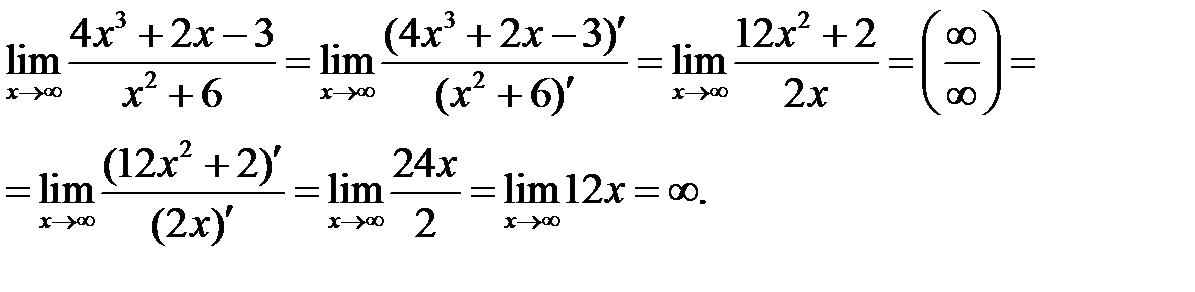
б) 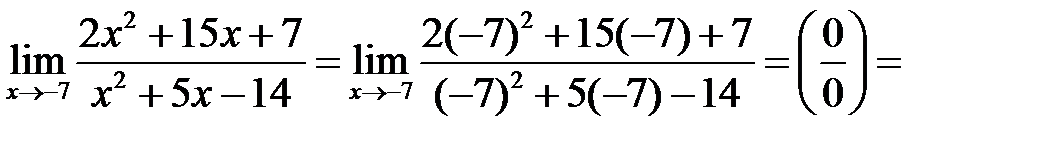
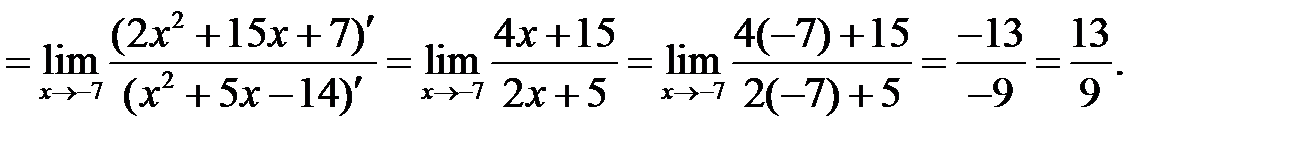
Дата: 2019-04-23, просмотров: 426.