Определенный интеграл, его вычисление и свойства

Определенный интеграл от функции 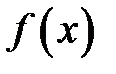, непрерывной на отрезке 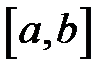, вычисляется по формуле:

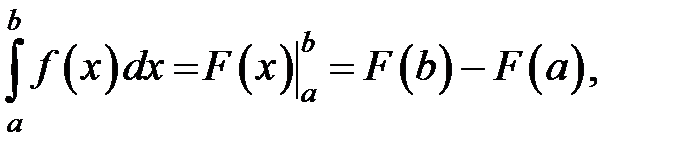(5)

где 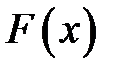— первообразная для функции 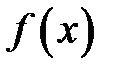, т. е.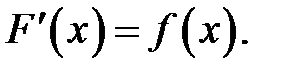

Формула (5) называется формулой Ньютона — Лейбница.

Свойства определенного интеграла:

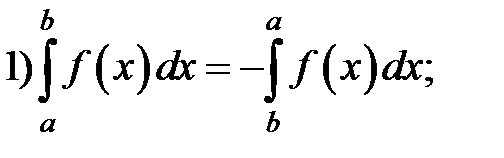
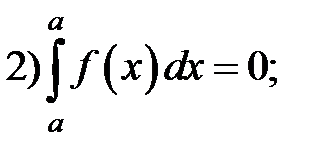
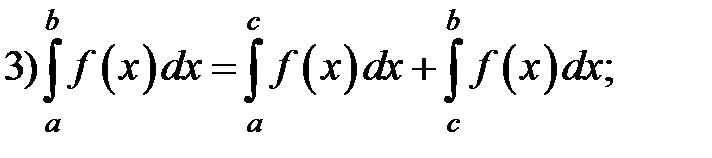
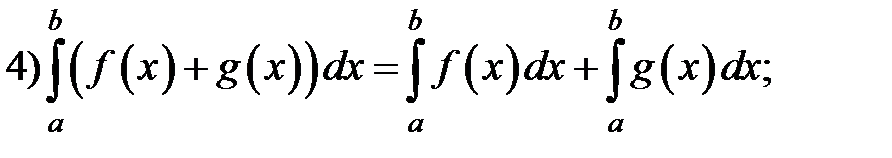
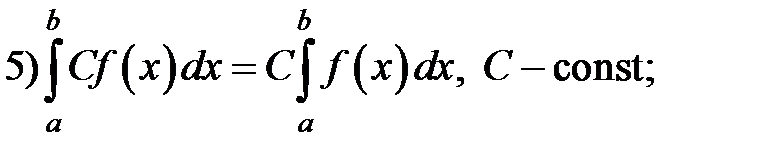
6) Если 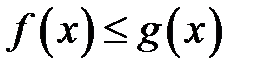 для всех 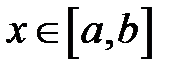, то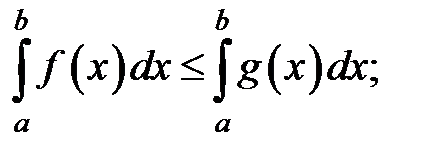

7) Если 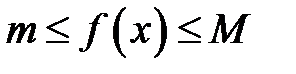 для всех 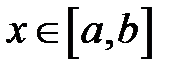, то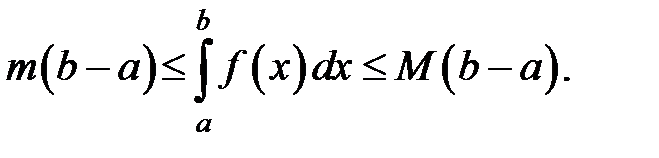

При вычислении определенного интеграла для нахождения первообразной используют те же методы, что и для нахождения неопределенного интеграла, т. е. замену переменной, интегрирование по частям и т. д. Однако есть ряд особенностей. При замене переменной по формуле (1) необходимо в соответствии с заменой менять пределы интегрирования:

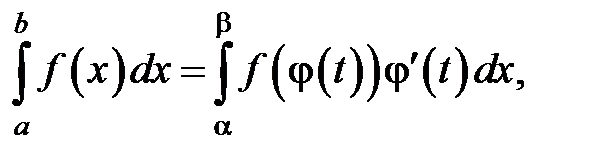(6)

где 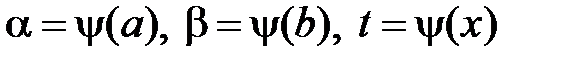 — обратная к  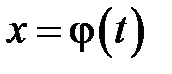функция.

Формула интегрирования по частям (3) приобретает вид:

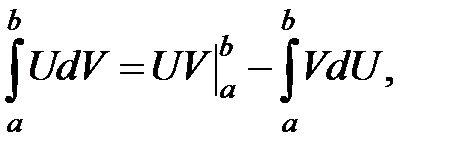                     (7)

    Пример 4. Вычислить определенный интеграл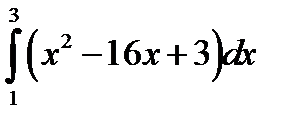

Решение.

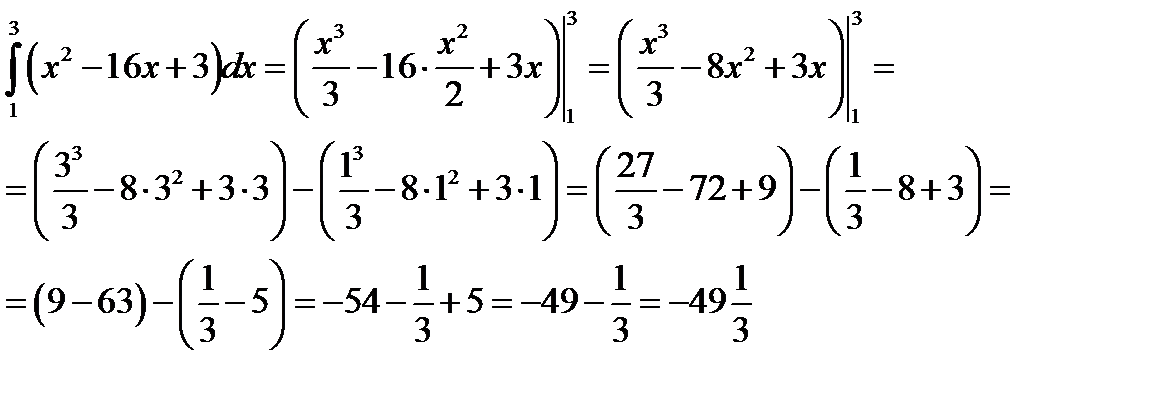
Площади плоских фигур

1. Вычисление площадей плоских фигур в декартовой системе координат

Если плоская фигура (рис. 1) ограничена линиями 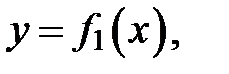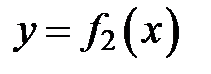, где 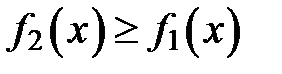 для всех 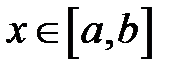, и прямыми 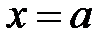, , 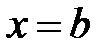то ее площадь вычисляется по формуле:

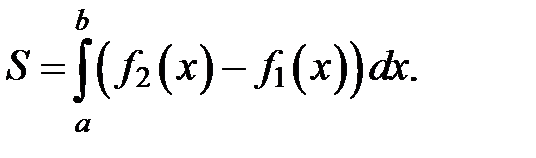               (8)

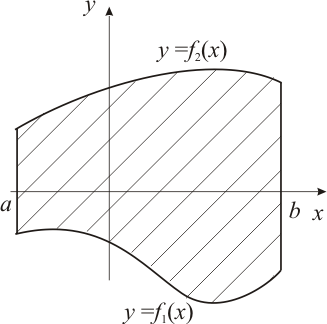
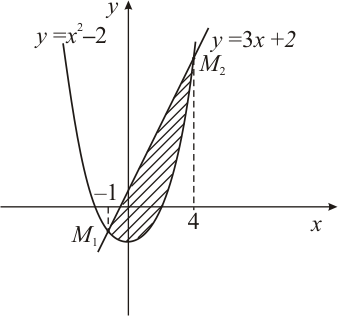
Рис. 1	Рис. 2

Пример. Найти площадь фигуры, ограниченной линиями:

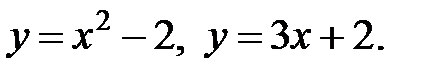
Решение. Построим схематический рисунок (рис. 2). Для построения параболы возьмем несколько точек:

Для построения прямой достаточно двух точек, например 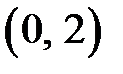 и .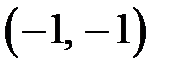

Найдем координаты точек 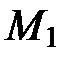 и 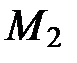 пересечения параболы  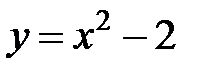и прямой .

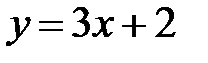Для этого решим систему уравнений

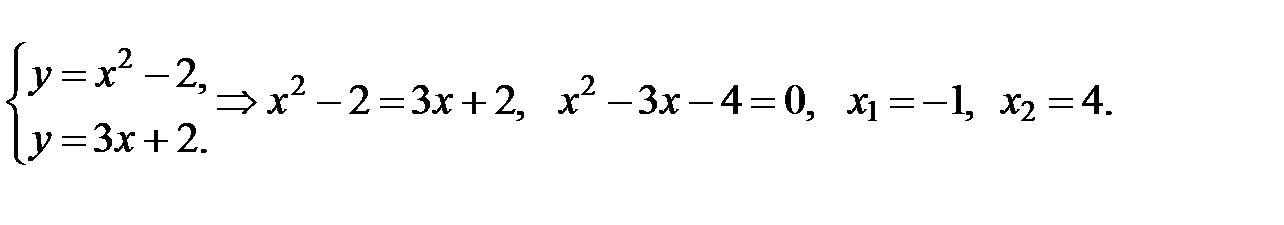
Тогда 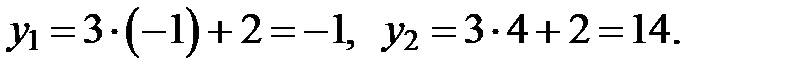 Итак,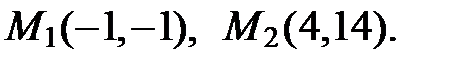

Площадь полученной фигуры найдем по формуле (8), в которой

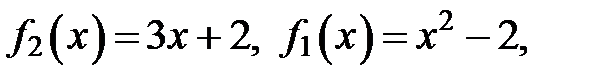 поскольку  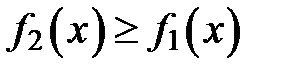для всех 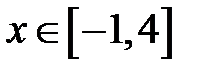. Получим:

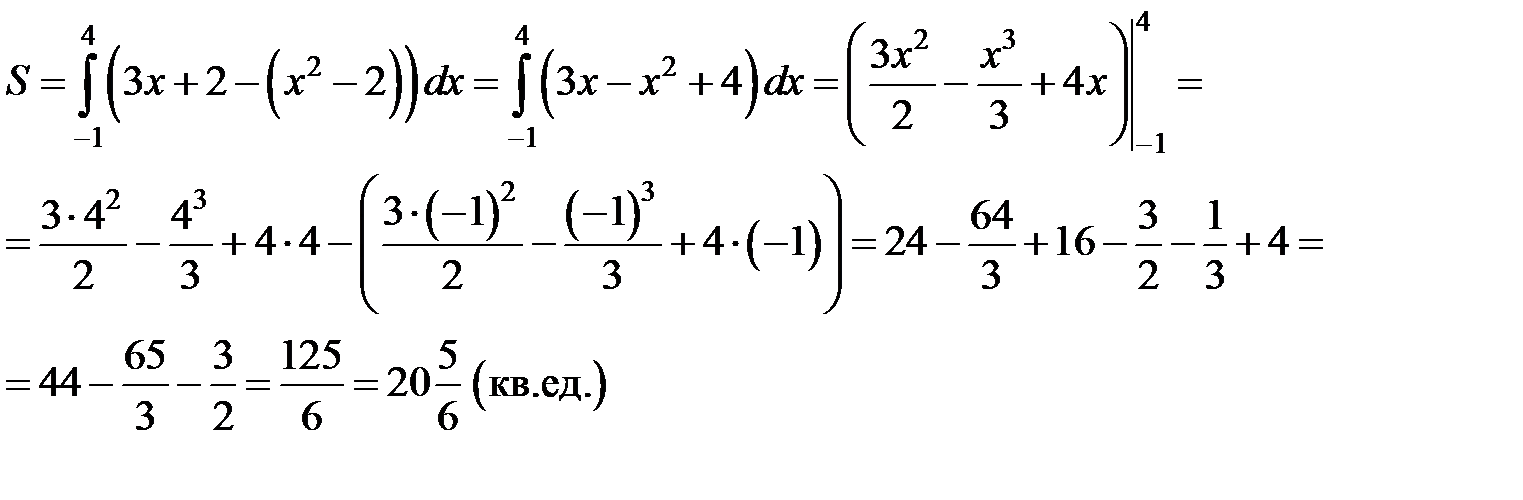
2. Вычисление площадей фигур, ограниченных линиями, заданными параметрически

Если функци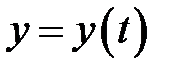и  и 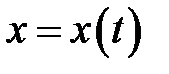 имеют непрерывные производные первого порядка для всех 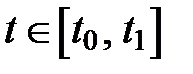, то площадь плоской фигуры, ограниченной линией  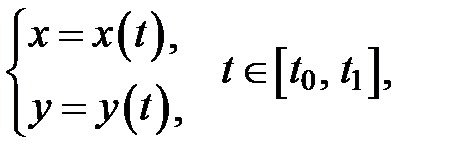прямыми x = a, x = b, где a = x(t₀),

b = x(t₁), и осью OX, вычисляется по формуле:

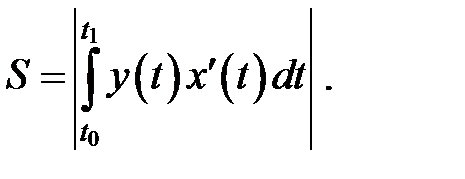           (9)

Пример. Найти площадь фигуры, ограниченной линиями, заданными параметрически:

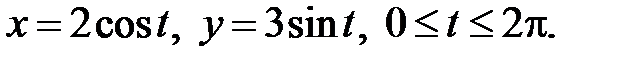
Решение. Для построения фигуры составим таблицу значений координат (x, y) точек кривой, соответствующих различным значениям параметра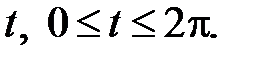

t	0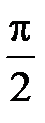
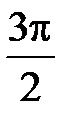
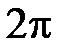
x	2	0	–2	0	2
y	0	3	0	–3	0

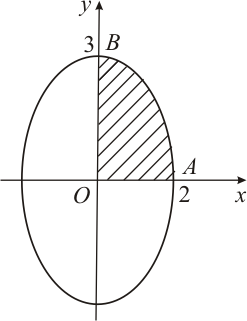
Рис. 3

Нанесем точки (x, y) на координатную плоскость XOY и соединим плавной линией. Когда параметр 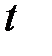изменяется от  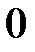до 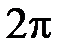, соответствующая точка  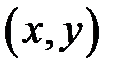описывает эллипс (известно, что  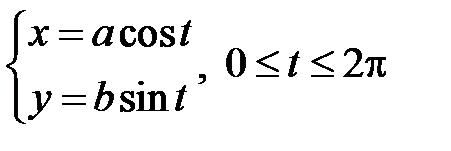— параметрические формулы, задающие эллипс с полуосями a и b). Учитывая симметрию фигуры относительно координатных осей OX и OY, найдем её площадь S, умножив на 4 площадь криволинейной трапеции AOB. Согласно формуле (9) получим:

Длина дуги плоской кривой

1. Вычисление дуги плоской кривой в декартовых координатах

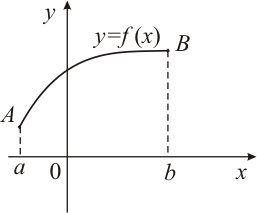
Рис. 4

Если кривая задана уравнением 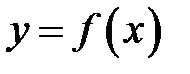, функция  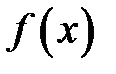имеет непрерывную первую производную при всех 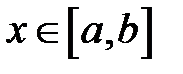, то длина дуги  (рис. 4) этой кривой, заключенной между точкам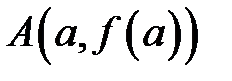и  и 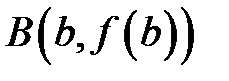, вычисляется по формуле:

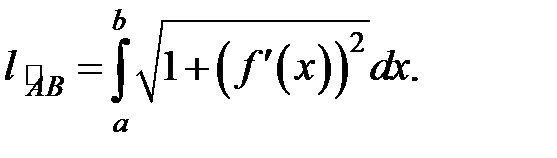  (10)

2. Вычисление длины дуги кривой, заданной параметрически

Если кривая задана параметрически 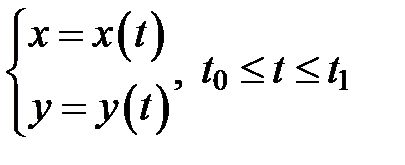, и функции  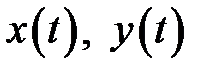имеют непрерывные производные 1-го порядка при всех 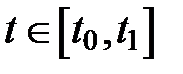, то длина дуги 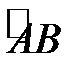, соответствующей изменению параметра от  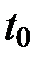до 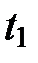, вычисляется по формуле:

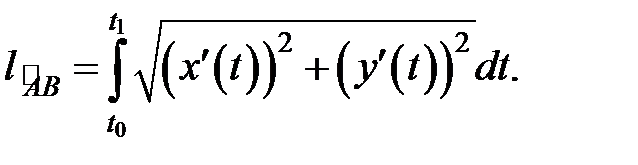       (11)

Пример. Найти длину дуги кривой

а) 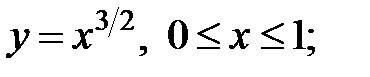б)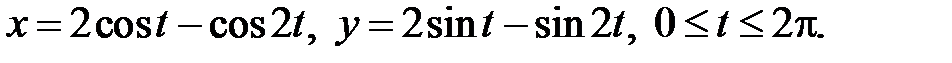

Решение.

а) Так как кривая задана в декартовой системе координат уравнением 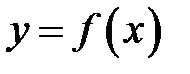, то для вычисления длины дуги воспользуемся формулой (10). Найдем 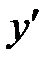:  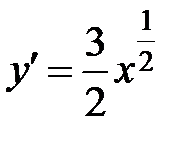          и подставим в (10):

б)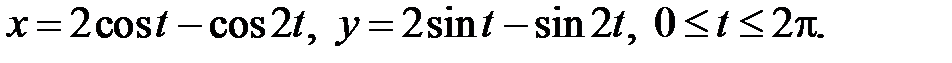

Кривая задана параметрически, поэтому воспользуемся формулой (11). Найдем :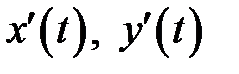

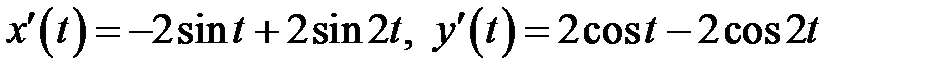и подставим в (11):

Вычисление объемов тел вращения

Если тело образовано вращением вокруг оси OX криволинейной трапеции, ограниченной кривой 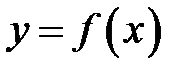, осью OX и прямыми 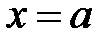,  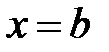(рис. 5), то его объем вычисляется по формуле:

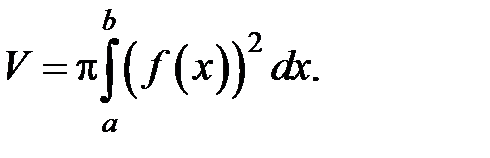                 (12)

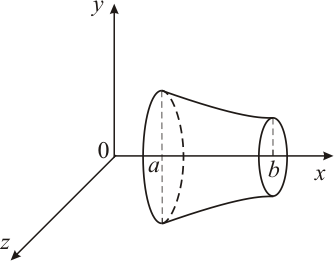
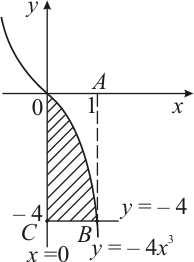
Рис. 5	Рис. 6

Пример. Найти объем тела, полученного вращением вокруг оси OX фигуры, ограниченной линиями: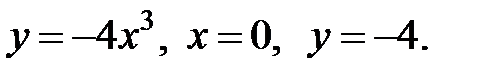

Решение. Построим криволинейную трапецию, вращением которой получается тело вращения (рис. 6).

Чтобы получить объем тела вращения из объема 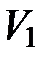 тела, полученного вращением фигуры ОАВС, вычтем объем  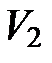тела, полученного вращением фигуры ОАВ. Тогда искомый объем 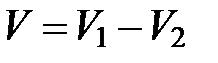. По формуле (12) найдем  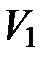и 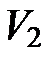:  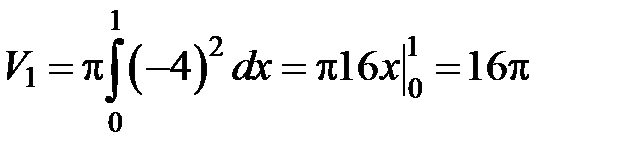(ед. объема);

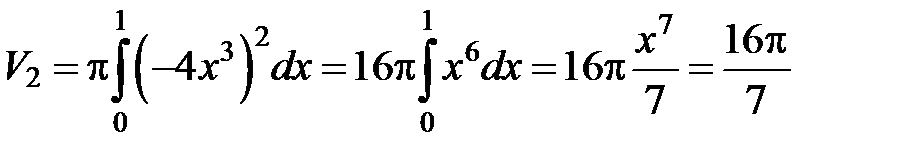 (ед. объема);

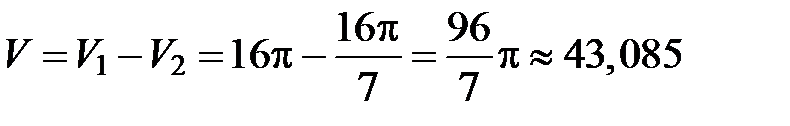(ед. объема).