Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Если каждому натуральному числу n поставлено в соответствие число х_n, то говорят, что задана последовательность

x_1, х₂, …, х_n = {x_n}

 

Общий элемент последовательности является функцией от n.

x_n = f(n)

Таким образом последовательность может рассматриваться как функция порядкового номера элемента.

Задать последовательность можно различными способами – главное, чтобы был указан способ получения любого члена последовательности.

 

Пример. {x_n} = {(-1)ⁿ} или {x_n} = -1; 1; -1; 1; …

              {x_n} = {sinpn/2} или {x_n} = 1; 0; 1; 0; …

 

Для последовательностей можно определить следующие операции:

 

1) Умножение последовательности на число m: m{x_n} = {mx_n}, т.е. mx₁, mx₂, …

2) Сложение (вычитание) последовательностей: {x_n} ± {y_n} = {x_n ± y_n}.

3) Произведение последовательностей: {x_n}×{y_n} = {x_n×y_n}.

4) Частное последовательностей: 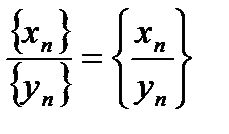 при {y_n} ¹ 0.

                           Ограниченные и неограниченные последовательности.

Последовательность {x_n} называется ограниченной, если существует такое число М>0, что для любого n верно неравенство: 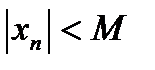, т.е. все члены последовательности принадлежат промежутку (-М; M).

 

Последовательность {x_n}называется ограниченной сверху, если для любого n существует такое число М, что x_n £ M.

 

Последовательность {x_n}называется ограниченной снизу, если для любого n существует такое число М, что x_n ³ M

 

Пример. {x_n} = n – ограничена снизу {1, 2, 3, … }.

Число а называется пределом последовательности {x_n}, если для любого положительного e>0 существует такой номер N, что для всех n > N выполняется условие: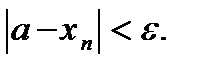

Это записывается: lim x_n = a.

В этом случае говорят, что последовательность {x_n}сходится к а при n®¥.

Свойство: Если отбросить какое- либо число членов последовательности, то получаются новые последовательности, при этом если сходится одна из них, то сходится и другая.

Пример. Доказать, что предел последовательности lim .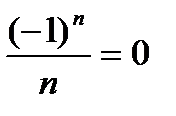

Пусть при n > N верно 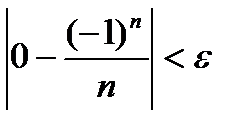, т.е. 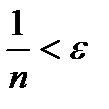. Это верно при 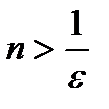, таким образом, если за N взять целую часть от 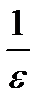, то утверждение, приведенное выше, выполняется.

Пример. Показать, что при n®¥ последовательность 3, 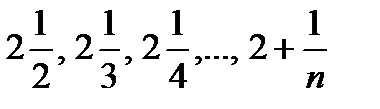 имеет пределом число 2.

Итого: {x_n}= 2 + 1/n; 1/n = x_n – 2

Очевидно, что существует такое число n, что 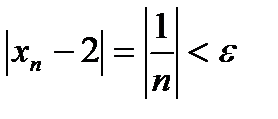, т.е. lim {x_n} = 2.

Теорема. Последовательность не может иметь более одного предела.

Теорема. Если x_n ® a , то последовательность { x_n } ограничена.

Следует отметить, что обратное утверждение неверно, т.е. из ограниченности последовательности не следует ее сходимость.

Например, последовательность 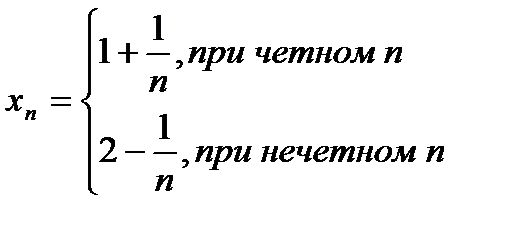не имеет предела, хотя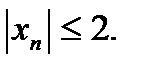

 

Монотонные последовательности.

 

Определение. 1) Если x_n+1 > x_n для всех n, то последовательность возрастающая.

         2) Если x_n+1 ³ x_n для всех n, то последовательность неубывающая.

             3) Если x_n+1 < x_n для всех n, то последовательность убывающая.

             4) Если x_n+1 £ x_n для всех n, то последовательность невозрастающая

Все эти последовательности называются монотонными. Возрастающие и убывающие последовательности называются строго монотонными.

Пример. {x_n} = 1/n – убывающая и ограниченная

           {x_n} = n – возрастающая и неограниченная.

Пример. Доказать, что последовательность {x_n}= 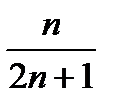 монотонная возрастающая.

Найдем член последовательности {x_n+1}=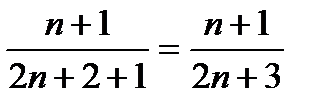

Найдем знак разности: {x_n}-{x_n+1}=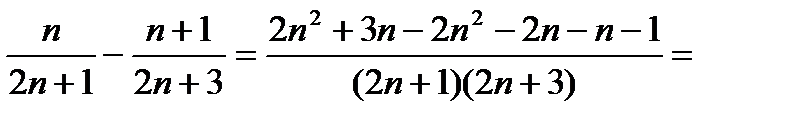

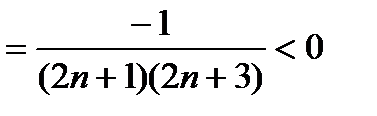, т.к. nÎN, то знаменатель положительный при любом n.

Таким образом, x_n+1 > x_n. Последовательность возрастающая, что и следовало доказать.

Пример. Выяснить является возрастающей или убывающей последовательность {x_n} = .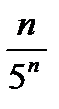

Найдем 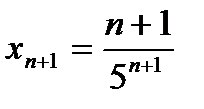. Найдем разность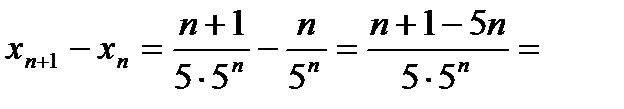

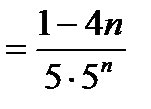, т.к. nÎN, то 1 – 4n <0, т.е. х_n+1 < x_n. Последовательность монотонно убывает.

Следует отметить, что монотонные последовательности ограничены по крайней мере с одной стороны.

 

Теорема. Монотонная ограниченная последовательность имеет предел

Рассмотрим последовательность {x_n} = .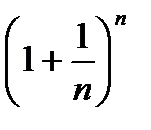

Если последовательность {x_n} монотонная и ограниченная, то она имеет конечный предел.

Итак, последовательность 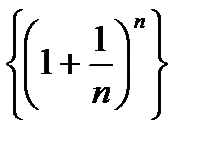- монотонно возрастающая и ограниченная сверху, т.е. имеет конечный предел. Этот предел принято обозначать буквой е.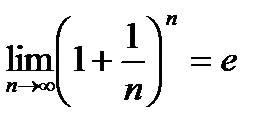

Предел функции в точке, в бесконечности. Основные теоремы о пределах.

Предел функции в точке.

 

                                   y                        f(x)

 

                                     

                                        A + e

                                             A

                                         0A - e        a - D a a + D x

 

 

Пусть функция f(x) определена в некоторой окрестности точки х = а (т.е. в самой точке х = а функция может быть и не определена)

Число А называется пределом функции f(x) при х®а, если для любого e>0 существует такое число D>0, что для всех х таких, что

0 < ïx - aï < D

верно неравенство                           ïf(x) - Aï< e.

То же определение может быть записано в другом виде:Если а - D < x < a + D, x ¹ a, то верно неравенство А - e < f(x) < A + e.

Запись предела функции в точке: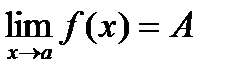

Если f(x) ® A₁ при х ® а только при x < a, то 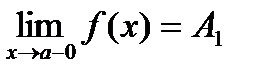 - называется пределом функции f(x) в точке х = а слева, а если f(x) ® A₂ при х ® а только при x > a, то  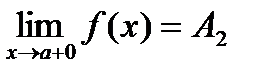называется пределом функции f(x) в точке х = а справа.

 

                                               у

                                                                                         f(x)

 

                                                   А₂

 

                                                   А₁ 0       a                           x

 

                                                                                   

    Приведенное выше определение относится к случаю, когда функция f(x) не определена в самой точке х = а, но определена в некоторой сколь угодно малой окрестности этой точки.

Пределы А₁ и А₂ называются также односторонними пределами функции f(x) в точке х = а. Также говорят, что А – конечный предел функции f(x).

Предел функции при стремлении аргумента к бесконечности.

Число А называется пределом функции f(x) при х®¥, если для любого числа e>0 существует такое число М>0, что для всех х, ïхï>M выполняется неравенство

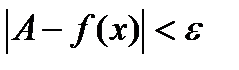
При этом предполагается, что функция f(x) определена в окрестности бесконечности.

Записывают: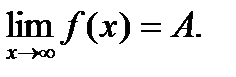                                    

Графически можно представить:                              

 

    y                                                      y

 

 

    A                                                     A

            0                              х                  0                             х

 

 

                                                      

                                                                                           

    y                                                      y

 

 

    A                                                     A

 

          0                               x                        0                                    x

 

                                                                 

                                                                                                                

 

Аналогично можно определить пределы 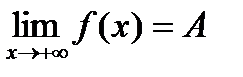 для любого х>M и  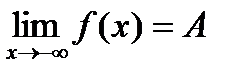для любого х<M.

Основные теоремы о пределах.

1. 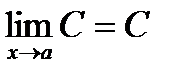, где С = const

Следующие теоремы справедливы при предположении, что функции f(x) и g(x) имеют конечные пределы при х®а.

2.

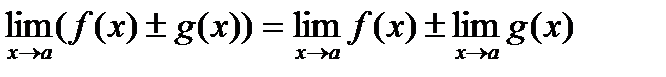
3.

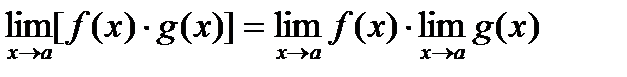
Следствие.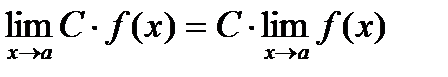

4. 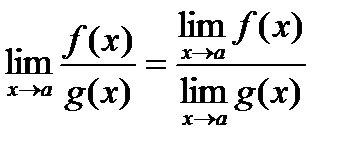при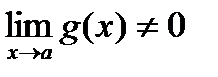

5.Если f ( x )>0 вблизи точки х = а и , то А>0.

Аналогично определяется знак предела при f(x) < 0, f(x) ³ 0, f(x) £ 0.

6. Если g ( x ) £ f ( x ) £ u ( x ) вблизи точки х = а и 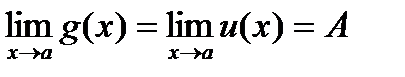, то и .

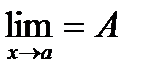Функция f(x) называется ограниченной вблизи точки х = а, если существует такое число М>0, что ïf(x)ï<M вблизи точки х = а.

7.Если функция f ( x ) имеет конечный предел при х ® а, то она ограничена вблизи точки х = а.

Функция f(x) называется бесконечно малой при х®а, где а может быть числом или одной из величин ¥, +¥ или -¥, если .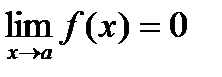

    Бесконечно малой функция может быть только если указать к какому числу стремится аргумент х. При различных значениях а функция может быть бесконечно малой или нет.

Пример. Функция f(x) = xⁿ является бесконечно малой при х®0 и не является бесконечно малой при х®1, т.к. .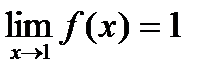

 

Теорема. Для того, чтобы функция f ( x ) при х ® а имела предел, равный А, необходимо и достаточно, чтобы вблизи точки х = а выполнялось условие

f ( x ) = A + a ( x ),

где a (х) – бесконечно малая при х ® а ( a (х) ® 0 при х ® а).

 

Свойства бесконечно малых функций:

 

1) Сумма фиксированного числа бесконечно малых функций при х®а тоже бесконечно малая функция при х®а.

2) Произведение фиксированного числа бесконечно малых функций при х®а тоже бесконечно малая функция при х®а.

3) Произведение бесконечно малой функции на функцию, ограниченную вблизи точки х = а является бесконечно малой функцией при х®а.

4) Частное от деления бесконечно малой функции на функцию, предел которой не равен нулю есть величина бесконечно малая.