Величина наращенной суммы за время t с учетом инфляции (индекс инфляции – I(t)p) и номинальной сложной процентной ставки r c m начислениями в год будет рассчитываться по формуле:
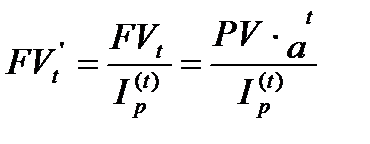 , где
, где 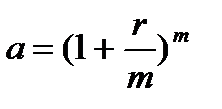 . (3.20)
. (3.20)
Следовательно, для ликвидации эрозии капитала, необходимо выполнение неравенства:
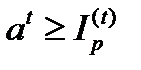 или
или 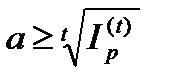 .
.
Процентную ставку, при которой имеет место строгое равенство, обозначим r* и определим ее значение
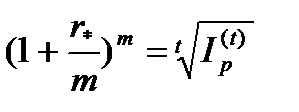 или
или 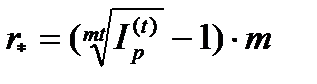 . (3.21)
. (3.21)
Ставка r при которой имеет место реальное накопление капитала (r > r*) называется положительной процентной ставкой.
Если за время t наращения капитала известен годовой темп инфляции h, то годовой индекс инфляции равен
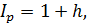
а индекс инфляции за t лет будет
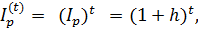
то формула (3.21) примет вид:
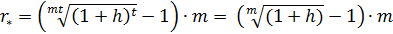 (3.22)
(3.22)
При m = 1, получим
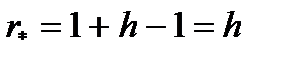
Следовательно, реальное наращение капитала при заданном годовом темпе инфляции h за время t лет будет при ставке
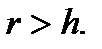
Обеспечение реальной доходности в условиях инфляции
Для обеспечения реальной доходности, согласно коэффициенту наращения a (наращение по процентной ставке r с m начислениями в год) необходимо так индексировать исходную ставку (увеличить ее на инфляционную премию), чтобы новый коэффициент наращения a1 (наращение по процентной ставке r1 с m начислениями в год) компенсировал потери из-за инфляции. Следовательно, a1 можно определить из равенства:
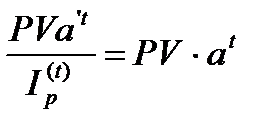 или
или 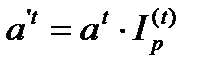 или
или 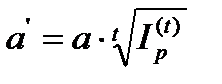
Из последнего выражения, принимая во внимание, коэффициенты наращение по процентной ставке r и r1 с m - начислениями процентов в год в течении t лет, имеем
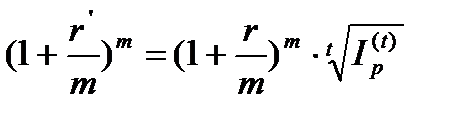 (3.23)
(3.23)
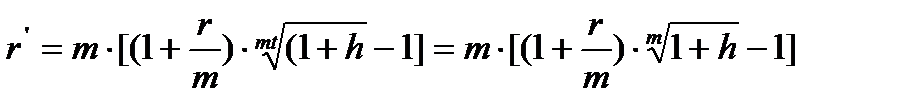 (3.24)
(3.24)
В случае m = 1, получим формулу Фишера
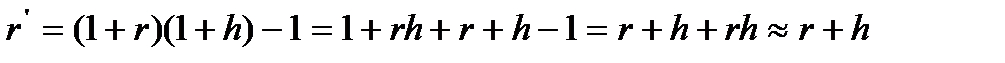 (3.25)
(3.25)
Пример.
Банк предлагает клиентам помещать деньги на депозит на один год под 12% годовых с ежеквартальном начислением сложных процентов. Найти реальную доходность такого предложения для клиентов банка, если ежемесячный индекс инфляции прогнозируется равным 1,008.
Решение.
1) Индекс инфляции за 1 год равен (2.15)
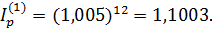
2) Из (3.23) определяем реальную доходность
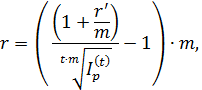
или
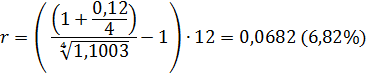
Пример.
На вклад 300 000 руб. ежемесячно начисляются сложные проценты по номинальной годовой процентной ставке 40%. Оцените сумму вклада через 1,5 года с точки зрения эрозии капитала, если ожидаемый темп инфляции 2% в месяц. Какова должна быть величина положительной процентной ставки?
Решение.
1) Индекс инфляции за 1,5 года (2.15) равен
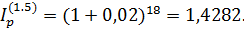
2) Применяя (3.20), находим сумму вклада с точки зрения эрозии капитала
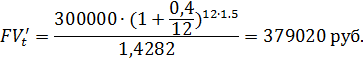
Тогда реальный доход владельца вклада будет
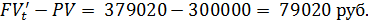
3) Положительная процентная ставка должна удовлетворять неравенству, следующему из (3.21)
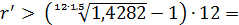 0,24 (24%).
0,24 (24%).
Замена платежей и сроков их выплат
При замене платежей должен выполняться принцип финансовой эквивалентности, который в математическом плане записывается системой уравнений.
Дата: 2019-04-22, просмотров: 728.