Пусть в течение базового периода денежные поступления происходят p раз в размере с ед. в начале каждого р-подпериода, а сложные проценты начисляются m раз по ставке r. Всего базовых периодов n.  Тогда будущая и приведенная стоимости данного р-срочного аннуитета пренумерандо рассчитываются следующим образом.

1) Будущая стоимость р - срочного аннуитета (ренты) пренумерандо

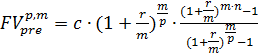                                       (4.5)

или

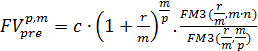                                        (4.6)

2) Приведенная стоимость р - срочного аннуитета (ренты) пренумерандо

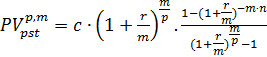                                      (4.7)

или

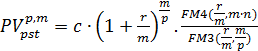                                        (4.8)

Здесь функции FM3(r,n) и FM4(r,n) имеют вид:

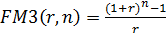— коэффициент наращения аннуитета (ренты);

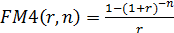 — коэффициент дисконтирования аннуитета (ренты).

Для данных функций составлены таблицы.

Данные формулы (4.1) - (4.8) включают большое количество вариантов оценки р-срочных аннуитетов (рент), необходимо только правильно определить параметры аннуитетов: n, p, m, r, c.

Пример.

В течение 5 лет в конце каждого полугодия на расчетный счет поступают равными долями платежи из расчета 8 млн. руб. в год на которые ежеквартально начисляются сложные проценты из расчета 20% годовых. Требуется определить сумму на расчетном счете к концу указанного срока. Найти размер платежей, при которых эта же сумма на расчетном счете накапливается за 4 года.

Решение.

Имеем постоянный р-срочный аннуитет постнумерандо.  

1) Параметры аннуитета: n=5, p=2, m=4, r=0,2, c=8/2=4 млн. руб.

Тогда по формуле (4.1) можно определить сумму на расчетном счете к концу указанного срока.

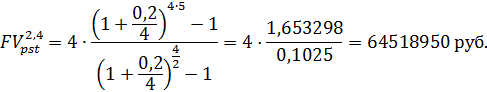
Или из формулы (4.2), используя таблицы для функций FM3(r,n) и FM4(r,n), следует

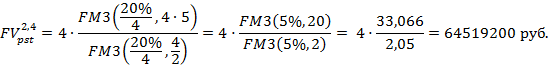
2) Для решения второй части задачи составим уравнение, где через х обозначен годовой платеж.

Параметры аннуитета: n=4, p=2, m=4, r=0,2, c=х/2

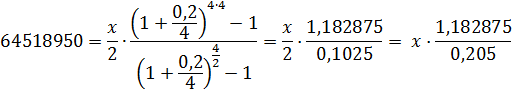
Из последнего уравнения следует, что при сроке инвестирования n=4 года и неизменных других параметрах, годовой платеж равен

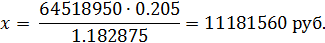
! Пример. Современная стоимость потока платежей

Какую сумму необходимо поместить в банк под номинальную процентную ставку 30% годовых, чтобы в течение 8 лет иметь возможность ежегодно получать 120 тыс. руб., снимая деньги равными долями каждые 3 месяца, и в конце 8-го года исчерпать счет полностью, если банком начисляются сложные проценты: а) ежегодно; б) по полугодиям.

Решение.

Имеем постоянный р-срочный аннуитет постнумерандо

а) Параметры аннуитета: n=8, p=4, m=1, r=0,3, c=120/4=30 тыс. руб.

Следовательно, по формуле (4.3) можно определить сумму которую необходимо поместить в банк в начале 8-ми летнего периода.

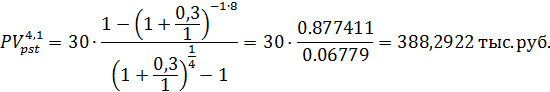
Или из формулы (4.4), используя таблицы для функций FM3(r,n) и FM4(r,n), имеем

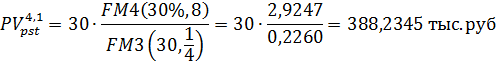
б) Параметры аннуитета: n=8, p=4, m=2, r=0,3, c=120/4=30 тыс. руб.

Поэтому по формуле (4.3):

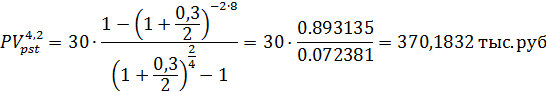
Замечание.

Ошибки в результатах объяснятся тем, что таблицы для функций FM3(r,n) и FM4(r,n) рассчитываются с ограниченной точностью и задаются с большим шагом по аргументам, что приводит часто к процедуре линейной интерполяции и дополнительной потере точности.