Под внутренней нормой доходности (IRR) понимают значение коэффициента дисконтирования r, при котором NPV равен нулю:
IRR = r, при котором NPV = f (r) = 0.
Итерационная формула для приближенного расчета IRR
IRR = r = r1 + f( r1) ∙ ( r1 - r2 ) / (f( r2) - f( r1)), (5.4)
где r1 - коэффициент дисконтирования при котором f( r1) > 0 или ( f( r1) < 0);
r2 - коэффициент дисконтирования при котором f( r2) < 0 или ( f( r2) > 0);
Формула верна, если
abs ( r1 - r2 ) ≤ 1 % (5.5)
Пример.
Найти значение IRR для проекта длительностью 3 года требующего инвестиций в сумме 10 млн. руб. с прогнозируемыми доходами по годам: 3 млн. руб., 4 млн. руб. и 7 млн. руб.
Решение.
1) Для расчета NPV = f (r) воспользуемся формулой (5.2) и проведем расчеты NPV для значений r в интервале от 5 % до 25% с шагом в 5%. Например, для r = 5%, имеем
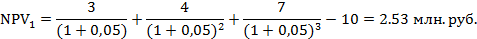
Проведя аналогичные расчеты для остальных значений r, сведем результаты в таблицу 1.
Табл. 1
| Коэффициент дисконтирования r в % | f ( r ) |
| 5,00 | 2,53 |
| 10,00 | 1,29 |
| 15,00 | 0,24 |
| 20,00 | -0,67 |
| 25,00 | -1,46 |
Проверим условие (5.5)
abs ( 15% - 20% ) = 5 %, что больше чем 1% и применять формулу (5.4) нельзя. Переходим к следующему приближению.
2) Проведем расчеты для значений r в интервале от 15% до 20% с шагом в 1%.
Табл. 2
| Коэффициент дисконтирования r в % | f ( r ) |
| 15,00 | 0,24 |
| 16,00 | 0,04 |
| 17,00 | -0,14 |
| 18,00 | -0,32 |
В данном случае условие (5.5)
abs ( 16% - 17% ) = 1 %,
выполняется и можно применить (5.4) для расчета IRR
IRR = r = 16% + 0,04 *( 16%-17%) / (-0,14-0,04) = 16,22 %
Ответ: Внутренняя ставка доходности данного проекта равна 16,22 %
Замечание. Рассчитать NPV и IRR данного проекта можно используя встроенные функции ЧПС и ВСД табличного процессора EXCEL
Задания для выполнения контрольной работы
Задание 1 . Темы «Процентные вычисления», «Потоки платежей». Задание выполняется с использованием методических рекомендаций по изучению дисциплины: Темы 2–4, учебных пособий из списка основной литературы [1; гл. 1, 2], [2; гл. 1, 2], учебного пособия, представленного в учебно-методическом комплексе (УМК) дисциплины:
Габескирия В.Я., Уродовских В.Н. Финансовая математика. Методические указания по выполнению лабораторной работы на ПЭВМ.
В задачах 1 – 17 выполнить различные коммерческие расчеты, используя данные, приведенные в таблице 1. Расчеты выполнить в среде Excel двумя способами:
1) с помощью математических формул и встроенных в Excel функций из категории «Математические»;
2) с помощью встроенных в Excel функций из категории «Дата и время» – ДОЛЯГОДА;
3) с помощью встроенных в Excel функций из категории «Финансовые» – БС, ПС, КПЕР, ЭФФЕКТ, НОМИНАЛ, ПЛТ и других.
Задача 1. Банк выдал ссуду размером Р рублей. Дата выдачи ссуды – Тн, возврата – Тк. День выдачи и день возврата считать за один день. Проценты рассчитываются по простой процентной ставке i% годовых.
Найти:
1) точные проценты с точным числом дней ссуды, обозначаемые как 365/365;
2) обыкновенные проценты с точным числом дней ссуды, обозначаемые как 365/360;
3) обыкновенные проценты с приближенным числом дней ссуды, обозначаемые как 360/360;
Задача 2. Сберегательный счет был открыт 3 января, и на него была положена сумма Р руб. Затем 20 марта со счета была снята сумма Р/5 руб., 20 апреля добавлена сумма в Р/10 руб. и 1 августа счет был закрыт. Все операции осуществлялись в течение года (простой год). Определить сумму полученную владельцем счета, если простая процентная ставка равнялась j% годовых и для начисления процентов применялся способ «365/360». Год обыкновенный.
Задача 3. Вкладчик разместил вначале года Р руб. в банке. Ставка рефинансирования ЦБ на момент заключения договора равна i % годовых. Договор предусматривает следующую схему начисления простых процентов: 1 квартал – 80% от ставки рефинансирования ЦБ, в каждом последующем квартале ставка понижается на 10% от ставки предыдущего квартала. Найти величину вклада через 1 год, если начисляются простые проценты.
Задача 4. Через Тдн дней предприятие должно получить по векселю S рублей. Банк приобрел этот вексель с дисконтом. Банк учел вексель по учетной ставке d% годовых (год равен 360 дням). Определить полученную предприятием сумму, дисконт и дисконтирующий множитель.
Задача 5. Платежи в S руб. и A руб. должны быть погашены соответственно через 150 и 300 дней. Кредитор и должник согласились заменить два платежа одним в сумме S+A руб. Найти срок оплаты консолидированного платежа, если используется простая процентная ставка i% и способ «360/360».
Задача 6. Инвестор, имеет сумму P руб., предполагает поместить ее на валютном депозите в СКВ на 9 мес. под i % годовых. Выяснить целесообразность этой сделки с банком, если в начале срока СКВ можно купить по курсу 27,7 руб. и ожидается, что через 9 мес. СКВ можно продать по курсу 28,2 руб. Годовая процентная ставка на рублевом депозите – (i+10)%. Проценты простые. Определить при каком курсе продажи схема с конвертацией в СКВ выгоднее простого депозита в рублях.
Задача 7. В кредитном договоре на сумму Р рублей и сроком на n лет зафиксирована ставка сложных процентов, равная i% годовых. Определить наращенную сумму и мультиплицирующий множитель. За сколько лет при ставке i% вклад вырастет в 3 раза?
Задача 8. Ссуда размером Р рублей представлена на n лет. Проценты сложные, ставка – j% годовых. Проценты начисляются m раз в году. Вычислить наращенную сумму. Определить срок, за который сумма Р удвоится при условиях данной задачи.
Задача 9. Вычислить эффективную ставку процента, если банк начисляет проценты m раз в году, исходя из номинальной ставки j% годовых.
Задача 10. Определить, какой должна быть номинальная ставка при начислении процентов m раз в году, чтобы обеспечить эффективную ставку i% годовых.
Задача 11. Через n лет предприятию будет выплачена сумме S рублей. Определить ее современную стоимость и дисконтирующий множитель при условии, что применяется сложная процентная ставка i% годовых.
Задача 12. Через n лет по векселю должна быть выплачена сумма S рублей. Банк учел вексель по сложной учетной ставке d% годовых. Определить дисконт.
Задача 13. На вклад P руб. ежемесячно начисляются сложные проценты по номинальной годовой процентной ставке j%. Оцените сумму вклада через 1,5 года с точки зрения эрозии капитала, если ожидаемый темп инфляции 0,5% в месяц. Какова должна быть величина положительной процентной ставки?
Задача 14. Три платежа P, 2·P и 3·P тыс. руб. со сроками выплат соответственно через 1 год, 2 года 6 месяцев и 3 года заменяются одним платежом, выплачиваемым через 2 года, при этом применяется сложная процентная ставка i% годовых. Найдите величину консолидированного платежа. Какой будет срок выплаты, если консолидированный платеж будет равен сумме исходных платежей?
Задача 15. Какую сумму необходимо поместить в банк под номинальную процентную ставку j% годовых, чтобы в течение n лет иметь возможность ежегодно получать R руб., снимая деньги равными долями каждые 3 месяца, и в конце n-го года исчерпать счет полностью, если банком начисляются сложные проценты m-раз в год.
Задача 16. В течение n лет на расчетный счет в конце каждого года поступает по R рублей, на которые m раз в году начисляются проценты по сложной годовой ставке j%. Определить сумму на расчетном счете к концу указанного срока для случаев ренты постнумерандо и пренумерандо.
Задача 17. Кредит в сумме А выдан на n лет по ставке сложных процентов j% годовых. Возврат кредита предполагается осуществлять в конце каждого месяца равными выплатами, включающими сумму основного долга и проценты. Определить вид потока платежей и найти величину погасительного платежа за месяц.
Таблица 1
| Вариант | Р, A, R | S | Tн | Тк | Тдн | n | i, j, d | m |
| 1 | 500000 | 10000000 | 23.01.2013 | 17.03.2013 | 180 | 2 | 8.0 | 12 |
| 2 | 1000000 | 9800000 | 24.01.2013 | 18.03.2013 | 180 | 3 | 8.5 | 12 |
| 3 | 1500000 | 9600000 | 30.01.2013 | 19.03.2013 | 180 | 4 | 9.0 | 2 |
| 4 | 2000000 | 9400000 | 31.01.2013 | 20.03.2013 | 180 | 10 | 9.5 | 2 |
| 5 | 2500000 | 9200000 | 01.02.2013 | 15.03.2013 | 180 | 11 | 10.0 | 2 |
| 6 | 3000000 | 9000000 | 28.01.2013 | 16.03.2013 | 90 | 12 | 10.5 | 4 |
| 7 | 3500000 | 8800000 | 29.01.2013 | 11.03.2013 | 90 | 8 | 11.0 | 4 |
| 8 | 4000000 | 8600000 | 25.01.2013 | 12.03.2013 | 90 | 9 | 11.5 | 2 |
| 9 | 4500000 | 8400000 | 27.01.2013 | 13.03.2013 | 90 | 5 | 12.0 | 12 |
| 10 | 5000000 | 8200000 | 26.01.2013 | 14.03.2013 | 90 | 6 | 12.5 | 4 |
Задание 2 . Тема «Анализ инвестиционных проектов». Задание выполняется с использованием методических рекомендаций по изучению дисциплины: Тема 5.
Решить задачу, используя данные, приведенные в таблице 1. Расчеты выполнить в среде Excel двумя способами:
1) с помощью математических формул и встроенных в Excel функций из категории «Математические»;
2) с помощью встроенных в Excel функций из категории «Финансовые» – ЧПС, ВСД.
Задача. Инвестиционный проект рассчитан на n лет и требует начальных инвестиций в размере S рублей. Денежные поступления прогнозируются в сумме S·k/n в каждом году (k = 1,…,n). Рассчитать приведенную стоимость проекта (NPV) и внутреннюю ставку доходности (IRR), если ставка дисконтирования равна d%. Сделать выводы.
Задание 3 . Тема «Портфель ценных бумаг». Задание выполняется с использованием лекции по Теме 6, учебных пособий [1; гл. 4], [2; гл. 4] из списка основной литературы.
Составить экономико-математические модели задач. Выполнить решение по формулам и с привлечением надстройки Excel «Поиск решений». Оптимальный портфель (доли ценных бумаг) представить в виде круговой диаграммы.
Вариант 1. Пусть портфель состоит из двух независимых бумаг с доходностями и рисками соответственно (0,1;0.4), (0.2;0.6). Найти портфель минимального риска, его риск и доходность.
Вариант 2. Пусть портфель состоит из двух независимых бумаг с доходностями и рисками соответственно (0.2;0.6) и (0.4;0,8). Найти портфель минимального риска, его риск и доходность.
Вариант 3. Пусть портфель состоит из двух независимых бумаг с доходностями и рисками соответственно (0,1;0.5) и (0.4;0,9). Найти портфель минимального риска, его риск и доходность.
Вариант 4. Пусть портфель состоит из трех независимых бумаг с доходностями и рисками соответственно (0,1;0.5), (0.2;0.7) и (0.4;0,9). Найти портфель минимального риска, его риск и доходность.
Вариант 5. Пусть портфель состоит из трех независимых бумаг с доходностями и рисками соответственно (0,2;0.4), (0.3;0.6) и (0.5;0,8). Найти портфель минимального риска, его риск и доходность.
Вариант 6. Пусть портфель состоит из трех независимых бумаг с доходностями и рисками соответственно (0,1;0.5), (0.2;0.6) и (0.4;0,9). Найти портфель минимального риска, его риск и доходность.
Вариант 7. Необходимо сформулировать оптимальный портфель Марковица трех некоррелированных ценных бумаг с эффективностями и рисками: (4,20), (10,50), (40, 80). Нижняя граница доходности портфеля задана равной 15.
Вариант 8. Необходимо сформировать оптимальный портфель Марковица из трех некоррелированных ценных бумаг с эффективностями и рисками: (6,20), (12,50), (42, 80). Нижняя граница доходности портфеля задана равной 17.
Вариант 9. Сформировать портфель Тобина минимального риска из двух видов ценных бумаг: безрисковой с эффективностью 2 и рисковой с эффективностью 10 и риском 5. Доходность портфеля равна 8.
Вариант 10. Сформировать портфель Тобина минимального риска из трех видов ценных бумаг: безрисковой с эффективностью 2 и некоррелированных рисковых с ожидаемыми эффективностями 4 и 10 и рисками 2 и 4. Доходность портфеля равна 8.
Задание 4. Тема «Портфель ценных бумаг». Задание выполняется с использованием лекции по Теме 6 и файла Excel «Построение портфеля по статданным», учебных пособий [1; гл. 4], [2; гл. 4] из списка основной литературы.
Задача. Сформулировать и решить задачу на построение портфеля Марковица или Тобина, используя реальные данные о котировках цен на различные финансовые инструменты на фондовом рынке.
Задание 5 . Тема «Облигации». Задание выполняется с использованием лекции и практического занятия по Теме 3, учебных пособий [1; гл. 5], [2; гл. 5], из списка основной литературы.
В задачах 1 – 3 выполнить расчеты параметров облигаций, используя данные, приведенные в таблице 2. Расчеты выполнить в среде Excel двумя способами:
1) с помощью математических формул и встроенных в Excel функций из категории «Математические»;
2) с помощью встроенных в Excel функций из категории «Финансовые».
Задача 1. Номинал облигации равен N руб., купон выплачивается один раз в год по ставке – с%, до погашения остается n лет. На рынке доходность на инвестиции с уровнем риска, соответствующим данной облигации, оценивается в r %. Определить текущую стоимость облигации.
Задача 2. Облигация со сроком погашения через n лет погашается по номиналу N руб. По облигации выплачивается ежегодный купонный доход в размере c% от номинала. Рыночная цена облигации составляет V руб. Определить доходность к погашению данной облигации. Сделайте выводы.
Задача 3. Номинал купонной облигации N руб., купон выплачивается один раз в год по ставке – c % годовых. До погашения облигации n лет, доходность до погашения составляет r%. Облигация торгуется по номиналу. Рассчитайте дюрацию Маколея для данной облигации. Сделайте выводы.
Таблица 2
| Вариант | N | V | n | c | r |
| 1 | 500 | 490 | 2 | 10.0 | 12.0 |
| 2 | 1000 | 950 | 3 | 9.0 | 11.0 |
| 3 | 1500 | 1480 | 4 | 8.5 | 10.0 |
| 4 | 2000 | 2100 | 5 | 8.0 | 13.0 |
| 5 | 2500 | 2600 | 6 | 7.5 | 14.0 |
| 6 | 3000 | 3150 | 5 | 7.0 | 12.0 |
| 7 | 3500 | 3400 | 4 | 6.5 | 11.5 |
| 8 | 4000 | 3950 | 3 | 6.0 | 11.0 |
| 9 | 4500 | 4400 | 2 | 5.5 | 10.5 |
| 10 | 5000 | 4900 | 2 | 5.0 | 10.0 |
Дата: 2019-04-22, просмотров: 745.