Методические рекомендации по изучению дисциплины
И выполнению контрольной работы
Для студентов,
обучающихся по направлениям подготовки
38.04.01 Экономика, 38.04.02 Менеджмент
(заочная форма обучения)
ОРЕЛ 2018
Методические указания обсуждены
на заседании кафедры «Математика, информатика и общегуманитарные дисциплины»
(Протокол № 01 от 14 сентября 2018 г.)
Зав. кафедрой – кандидат физико-математических наук, доцент
Е.С. Филонова
Введение
Дисциплина части образовательной программы, формируемой участниками образовательных отношений; модуль инвариантных дисциплин.
Цели дисциплины:
- развитие теоретико-практической базы и формирование уровня математической подготовки, необходимых для понимания основных идей применения математических методов финансовых расчетов в экономике, финансах и бизнесе;
- развитие математической базы и формирование уровня практической подготовки, необходимых для применения математических методов финансовых расчетов в финансовой деятельности и для решения задач финансового планирования.
Задача дисциплины:
- в результате изучения дисциплины «Математические методы финансовых расчетов» студенты должны владеть основными математическими понятиями дисциплины; уметь использовать методы финансовых вычислений для решения теоретических и прикладных задач экономики и финансов, уметь решать исследовательские задачи, иметь навыки работы со специальной математической литературой.
В процессе изучения дисциплины «Математические методы финансовых расчетов» студенты самостоятельно выполняют домашнюю контрольную работу.
Цели контрольной работы – усвоить теоретические основы дисциплины, выработать навыки в решении задач, соответствующих тематическому плану дисциплины, и овладеть математическими методами финансовых вычислений для решения прикладных и исследовательских задач экономики и финансов.
1. Методические указания по выполнению и оформлению контрольной работы
Контрольная работа по дисциплине «Математические методы финансовых расчетов» состоит из пяти заданий по различным темам курса.
В каждой задаче контрольной работы необходимо привести подробное решение и сделать обоснованные экономические выводы. Численное решение задач следует подкреплять использованием компьютерных технологий.
Решение заданий должно сопровождаться необходимыми комментариями, то есть все основные этапы решения задачи должны быть раскрыты и обоснованы соответствующими теоретическими положениями.
Варианты заданий определяются по последней цифре номера личного дела (зачетной книжки) студента.
Контрольная работа выполняется и защищается в сроки, установленные учебным графиком.
Титульный лист контрольной работы должен содержать все необходимые реквизиты:
- названия университета и филиала;
- название кафедры;
- направление подготовки;
- наименование учебной дисциплины;
- Ф.И.О. студента и номер его зачетной книжки;
- Ф.И.О. преподавателя;
- дату сдачи работы на проверку.
К собеседованию допускаются студенты, выполнившие правильно и в достаточном объеме все задания контрольной работы. Для получения зачета по результатам собеседования студент должен выполнить работу над ошибками в проверенной преподавателем контрольной работе, проработать теоретические основы методов решения задач и ответить на вопросы преподавателя.
Критерии и баллы текущего контроля по дисциплине
| № п.п. | Вид работы | Максимальное количество баллов |
| 1 | Посещаемость аудиторных занятий и активность работы на них | 6 |
| 2 | Выполнение задания № 1 контрольной работы | 15 |
| 3 | Выполнение заданий № 2-5 контрольной работы, в т.ч. | 14 |
| Задание № 2 | 3 | |
| Задание № 3 | 2 | |
| Задание № 4 | 6 | |
| Задание № 5 | 3 | |
| 4 | Подготовка и презентация творческого проекта | 5 |
ИТОГО за семестр
2. Основные формулы и примеры решения задач по теме «Теория процента. Простой процент»
2.1. Основные формулы финансовых операций с простыми процентами при постоянных: процентной ставке и временном интервале
Простой процент - это начисление процентов по периодам на первоначально инвестированную сумму.
В общем случае финансовой операции наращения по схеме простого процента формула имеет вид
FV = PV (1 + r ∙ t), (2.1)
где t – срок инвестирования в годах;
r – годовая процентная ставка в долях единицы;
PV – начальная сумма инвестирования;
FV – наращенная сумма по истечении t лет.
Множитель (1 + r ∙ t ) в формуле (2.1) называется множителем наращения или коэффициентом наращения простых процентов.
На практике многие финансовые операции выполняются в рамках одного года и тогда формула для начисления простого процента в течение периода времени, которое меньше года будет иметь вид
t
FV = PV ( 1 + r · ¾) , (2.2)
T
где FV - сумма, получаемая при начислении процента за t дней;
PV – первоначально инвестированная сумма;
t – количество дней начисления процента в течение года;
r - годовая процентная ставка в долях единицы;
T – длительность года в днях.
Заметим, что простые проценты
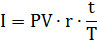
пропорциональны сроку вклада и процентной ставке.
Формула (2.2 ) носит общий характер, поскольку под t можно понимать любой интервал времени: день, месяц, квартал, год и т.д.. При этом показатель Т должен принимать соответствующие значения: 365 или 360, 12, 4, 1 и т.д.
Определяя продолжительность ссудо-заемной операции, принято день выдачи ссуды и погашения ее считать одним днем. При подсчете числа дней t срока ссудо-заемной операции в настоящее время применяются три схемы:
а) Способ «365/365». Точный процент и точная продолжительность периода (число дней в году 365 или 366 и t точное). Это наиболее точная схема и применяется в банках Великобритании и США.
б) Способ «365/360». Обыкновенный процент и точная продолжительность периода (число дней в году, квартале и месяце определяется приближенно, соответственно: 360, 90, 30 и t -точное). Эта схема дает несколько больший результат и применяется в банках Франции и Бельгии.
в) Способ «360/360». Обыкновенный процент и приблизительная продолжительность периода (число дней в году, квартале и месяце определяется приближенно, соответственно: 360, 90, 30 и t – приблизительное, т.к. считается, что в месяце 30 дней). Это менее точная схема и применяет в банках Германии, Дании и Швеции.
В предлагаемых схемах при расчете точного числа дней t пользуются специальными таблицами (одна для обычного года, а другая для високосного), в которых все дни года последовательно пронумерованы. Продолжительность финансовой операции определяется вычитанием номера первого дня из номера последнего дня.
В российской практике ссудо-заемных операций используются все три схемы.
Пример.
Инвестор размещает на счете в банке сумму 1000000 руб. под 20% годовых. Определить какую сумму получит вкладчик через 300 дней, используя в расчетах способ «360/360».
Решение.
Согласно (2.1) имеем
FV = 1000000 ( 1 + 0.2· 300/360 ) = 1666666,67 руб.
Пример.
Вкладчик размещает на счете в банке 75000 руб. Банк начисляет простые проценты раз в квартал по ставке 20% годовых. Найти процентный платеж и сумму, какую он получит через полтора года.
Решение.
Наращенную сумму рассчитаем по (2.2), а проценты по выражению для I представленному выше:
I = 75000 ·0.2∙ 6 / 4 = 22500 руб.;
FV = 75000 (1+0.2∙ 6 / 4) = 97500 руб.
! Пример. Начисление простых процентов
Вкладчик хочет разместить на счете в банке 75000 руб. Банк А начисляет простые проценты раз в месяц по ставке 20% годовых, а банк Б раз в полгода но по ставке 25% годовых. Определить, в каком из банков вкладчику необходимо разместить вклад, чтобы получить наибольший доход, если он намерен держать деньги в банке 2 года.
Решение.
Для анализа используем расчетную схему (2.2) для простых процентов:
FVА = 75000 (1+0.2∙ 24 / 12) = 105000 руб.;
FVБ = 75000 (1+0.25∙ 4 / 2) = 112500 руб.
Вкладчику необходимо разместить вклад в банке Б.
! Пример. Три варианта начисления простых процентов
Предоставлен кредит в размере 5 млн. руб. 25 января с погашением через 6 месяцев (25 июля) под 40% годовых. Рассчитать различными способами сумму к погашению, если год не високосный.
Решение.
Возможные варианты возврата кредита:
А) Точный процент и точное число дней.
Точное число дней определяется по таблицам с номерами дней года ( t = 206 – 25 = 181 дн.)
FV181 = 5·( 1 + 0,4 · 181/365 ) = 5,9918 млн. руб.
Б) Обыкновенный процент и точное число дней.
FV181 = 5·( 1 + 0,4· 181/360 ) = 6,0056 млн. руб.
В) Обыкновенный процент и приближенное число дней.
Приближенное число дней кредита равно: 5 дн. января (30 - 25) + 150 ( 30 дн. в 5 месяцах: февраль, март, апрель, май, июнь) + 25 дн. июля = 180 дн.
FV180 = 5 ·(1 + 0,4·180/360) = 6,0000 млн. руб.
2.2 Основные формулы финансовых операций с простыми процентами при переменных: процентной ставке и временном интервале
В практике финансовых расчетов, особенно при учете темпа инфляции, приходится часто изменять ставку простых процентов. Пусть в начальный момент времени инвестор вложил в некоторый банк сумму PV. За время инвестиционного периода t изменение годовой процентной ставки происходило m раз на следующих временных интервалах имеющих размерность в долях года:
t1, t2,t3, … , tm,
причем на каждом интервале годовая процентная ставка оставалась постоянной и была равна соответственно:
r1, r2, r3, … , rm
В этом случае наращенная сумма к концу инвестиционного периода будет
FV = PV+PV r1 t1+PV r2 t2 + … + PV rm tm = 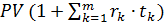 (2.3)
(2.3)
Пример.
Вкладчик разместил вначале года 100000 руб. в банке. Договор предусматривает следующую схему начисления простых процентов: 1 год – 20%, в каждом последующем полугодии ставка повышается на 10%. Найти величину вклада через 2 года, если проценты начисляются по схеме простых процентов.
Решение.
Применяя формулу (2.3), сумма вклада будет
FV2 = 100 000 (1 + 0,2·1+0,3· 0,5 + 0,4· 0,5) = 155 000 руб.
! Пример. Плавающая процентная ставка
Вкладчик разместил вначале года 50000 руб. в банке. Ставка рефинансирования[1] ЦБ на момент заключения договора равна 30% годовых. Договор предусматривает следующую схему начисления простых процентов: 1 квартал – 50% от ставки рефинансирования ЦБ, в каждом последующем квартале ставка понижается на 10% от ставки рефинансирования ЦБ. Найти величину вклада через 1 год, если проценты начисляются по схеме простых процентов.
Решение.
Определяя квартальные процентные ставки и применяя (2.3), рассчитаем величину вклада через год
FV1 = 50000 + 50000·0,15·0,25 + 50000· 0,12· 0,25 + 50000·0,09·0,25 +50000· 0,06· 0,25 = 50000·(1 + 0,0375 + 0,03 + 0,0225 + 0,015) = 55250 руб.
2.3 Процентный ключ (дивизор)
Процентный платеж в формуле (2.2) можно записать в виде
PV∙ t PV∙ t
I = = . (2.4)
Т / r D
Здесь D = Т/r называется процентным ключом, постоянным делителем или дивизором, а PV∙ t называется процентным числом.
Дивизор численно равен такому количеству денежных единиц, с которого при процентной ставке r получается 1 дн. ед. дохода в день.
Если процентная ставка r' выражается в процентах, то формула для расчета дивизора будет
D = 100 ∙ Т / r'
Пример.
Найти процентный платеж с капитала 5 000 руб., положенного в банк под 20% годовых на срок 200 дней, если расчет ведется способом «365/365».
Решение.
Воспользуемся выражением для дивизора и формулой (2.4).
D = 100 ∙ 365 / 20 = 1825
I = 5000 ∙ 200 / 1825 = 547,95 руб.
! Пример. Переменная сумма счета и начисление процентов
Сберегательный счет был открыт 3 января, и на него была положена сумма в 10 000 руб. Затем 20 марта со счета были сняты 2 000 руб., 20 апреля добавлена сумма в 1000 руб. и 1 августа счет был закрыт. Все операции осуществлялись в течение года (простой год). Определить сумму полученную владельцем счета, если процентная ставка равнялась 15% годовых, и для начисления процентов применялся способ «365/360». Год обыкновенный.
Решение.
Число дней: для 10000руб. (1 авг. (213) – 3 янв.(3) = 210 дн)
Для 2000 руб.(1 авг. (213) – 20 марта (79) = 134 дн)
Для 1000 руб.(1 авг. (213) - 20 апр. (110) = 103 дн)
Рассчитаем процентные числа
10000 ∙ 210 - 2000 ∙ 134 + 1000 ∙ 103 = 1935000
Дивизор равен
D = 360· 100 / 15 = 2400.
Следовательно, начисленные проценты равны
I = 1935000 / 2400 = 806,25 руб.,
и владелец счета получит
FV = 10000 –2000+1000 + 806,25 = 9806,25 руб.
2.4 Дисконтирование по простым процентам
.
2.4.1 Математическое дисконтирование
Это процесс обратный наращению капитала. При математическом дисконтировании решается задача нахождения первоначального капитала PV, который через t лет при наращении по схеме простого процента по годовой ставке r приведет к увеличению капитала до значения FV. Из формулы (2.1) следует, что
FV
PV = (2.5)
1 + r· t
В качестве ставки дисконтирования используется процентная ставка r. Разность между FV и PV называется дисконтом Dr.
FV· r · t
Dr = FV - PV = (2.6)
1 + r· t
Дисконт Dr не пропорционален ни времени, ни ставке процента r.
Пример.
Через полгода после заключения финансового соглашения о получении кредита должник обязан заплатить 2,14 млн. руб. Какова первоначальная величина кредита, если он выдан под 14 % годовых и начисляются обыкновенные проценты по схеме "360/360".
Решение.
Расчет ведем по формулам (2.5),(2.6):
PV = FV / (1+ r ∙ t / T ) = 2,14 / ( 1 + 0.14 ∙ 180 / 360 ) = 2 млн. руб.;
Dr = FV - PV = 2,14 - 2 = 0,14 млн. руб.
2.4.2 Банковское дисконтирование (банковский учет)
Существует дисконт, понимаемый как скидка с конечной суммы долга, который может быть установлен сразу в виде некоторой суммы или рассчитан на основе ставки дисконтирования. Этот дисконт называется банковским дисконтом и применяется для учета векселей.
Векселя могут оформляться по разному, однако чаще всего банку приходится иметь дело с суммой к погашению (номинальной стоимостью векселя), т.е. с величиной FV. В этом случае владелец векселя предъявляет его в банк для досрочного погашения. Банк соглашается его купить но, удерживая в свою пользу часть номинальной стоимости векселя, которая обычно называется дисконтом Dd. В этом случае банк предлагает владельцу сумму PV, исчисляемую исходя из объявленной банком ставки дисконтирования (учетной ставки) – d, которая будет меньше номинальной стоимости векселя. Дисконт Dd в этом случае представляет собой проценты начисленные за время t от дня дисконтирования до дня погашения и будет равен
Dd = FV·t ·d (2.7)
И владелец получит
PV = FV (1 - t d) (2.8)
Заметим, что математический дисконт Dr всегда положителен, а из формулы (2.8) следует, что
1 - t d > 0 или t < 1 / d
Если вексель погашается досрочно за t дней до даты законного погашения векселя, то из формулы (2.8) с учетом коэффициента учитывающего относительную длину периода до погашения - t / T , где Т число дней в году, получим следующую формулу для расчета выплачиваемой в этом случае банком суммы
t
PV = FV ( 1 – d ∙ ¾ ), (2.9)
T
а для дисконта, имеем
t
Dd = FV — d (2.10)
T
! Пример. Банковский учет
Векселедержатель предъявил для учета вексель на сумму 100 000 руб. со сроком погашения 28.09.2017г. Вексель предъявлен 13.09.2017г. Банк согласился учесть вексель с дисконтом в 50 % годовых. Найти сумму, которую получит векселедержатель по векселю.
Решение.
Количество дней от момента учета векселя до погашения:
28.09.2017г.(271). – 13.09.2017г.(256) = 15 дн.
По формуле (2.9) найдем сумму, которую получит векселедержатель
PV = 100000· (1 – 0,5 ∙ 15/360) = 97916,67 руб.
Потребительский кредит
Дата: 2019-04-22, просмотров: 764.